题目描述
Mayan puzzle 是最近流行起来的一个游戏。游戏界面是一个77 行 \times5×5 列的棋盘,上面堆放着一些方块,方块不能悬空堆放,即方块必须放在最下面一行,或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块,消除方块的规则如下:
- 每步移动可以且仅可以沿横向(即向左或向右)拖动某一方块一格:当拖动这一方块时,如果拖动后到达的位置(以下称目标位置)也有方块,那么这两个方块将交换位置(参见输入输出样例说明中的图 66 到图 77);如果目标位置上没有方块,那么被拖动的方块将从原来的竖列中抽出,并从目标位置上掉落(直到不悬空,参见下面图 11 和图 22);
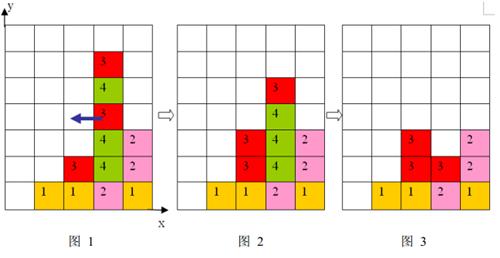
- 任一时刻,如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块,则它们将立即被消除(参见图1 到图3)。
注意:
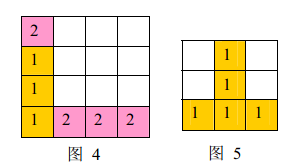
a) 如果同时有多组方块满足消除条件,几组方块会同时被消除(例如下面图 44,三个颜色为 11 的方块和三个颜色为 22 的方块会同时被消除,最后剩下一个颜色为 22 的方块)。
b) 当出现行和列都满足消除条件且行列共享某个方块时,行和列上满足消除条件的所有方块会被同时消除(例如下面图5 所示的情形,55 个方块会同时被消除)。
- 方块消除之后,消除位置之上的方块将掉落,掉落后可能会引起新的方块消除。注意:掉落的过程中将不会有方块的消除。
上面图 11 到图 33 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为 (0,0)(0,0),将位于 (3,3)(3,3) 的方块向左移动之后,游戏界面从图 11 变成图 22 所示的状态,此时在一竖列上有连续三块颜色为 44 的方块,满足消除条件,消除连续 33 块颜色为 44 的方块后,上方的颜色为 33 的方块掉落,形成图 33 所示的局面。
输入格式
共 66 行。
第一行为一个正整数 nn,表示要求游戏通关的步数。
接下来的 55 行,描述 7 \times 57×5 的游戏界面。每行若干个整数,每两个整数之间用一个空格隔开,每行以一个 00 结束,自下向上表示每竖列方块的颜色编号(颜色不多于 1010 种,从 11 开始顺序编号,相同数字表示相同颜色)。
输入数据保证初始棋盘中没有可以消除的方块。
输出格式
如果有解决方案,输出 nn 行,每行包含 33 个整数 x,y,gx,y,g,表示一次移动,每两个整数之间用一个空格隔开,其中 (x,y)(x,y) 表示要移动的方块的坐标,gg 表示移动的方向,11 表示向右移动,-1−1 表示向左移动。注意:多组解时,按照 xx 为第一关键字,yy 为第二关键字,11 优先于 -1−1,给出一组字典序最小的解。游戏界面左下角的坐标为 (0,0)(0,0)。
如果没有解决方案,输出一行 -1。
说明/提示
【输入输出样例说明】
按箭头方向的顺序分别为图 66 到图 1111
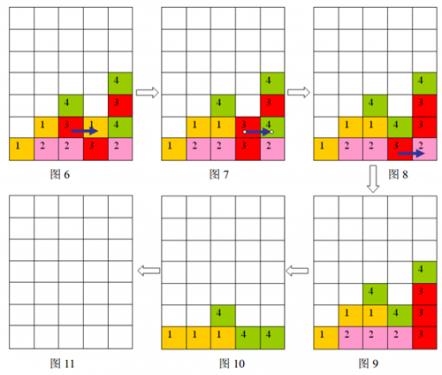
样例输入的游戏局面如上面第一个图片所示,依次移动的三步是:(2,1)(2,1) 处的方格向右移动,(3,1)(3,1) 处的方格向右移动,(3,0)(3,0) 处的方格向右移动,最后可以将棋盘上所有方块消除。
【数据范围】
对于 30\%30% 的数据,初始棋盘上的方块都在棋盘的最下面一行;
对于 100\%100% 的数据,0<n \le 50<n≤5。
题目很长啊~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
【分析】
问题的性质加上 3s 的运行时间告诉我们:这个世界需要暴力。
一个块向右交换,与它右边的块向左交换是等价的,但前者的字典序更小,所以不必考虑后者。
此外,如果一种颜色的数量在 1~2 之间,就可以直接剪枝。
与其说本题在考察搜索,不如说本题在考察选手的编程习惯和心理素质。很多人没有清晰明确的思路和良
好的编码习惯,结果“投降”,输出了“-1”,或者写了数 KB 代码却没有得到多少分。所以大家要养成好的编
程习惯,包括变量的命名、代码缩进、注释等,同时要发扬敢于使用暴力的精神。
【代码】
下面代码没有任何剪枝,但已经测试通过了。
#include <iostream>
#include <cstring>
using namespace std;
inline void swap(int &a, int &b) { int t=a; a=b; b=t; }
// 程序中使用横向棋盘,5行7列,水平移动变竖直移动,竖直移动变水平运动。
int n;
int map[7][6][9];
int a[6],b[6],c[6]; // 每一步的变化,a是棋盘倒放之后的行,b是列
// 方块下落
void fall(int depth)
{
for (int i=1; i<=5; i++)
{
int *m=map[depth][i];
// 在第i行中,寻找第一个0,然后再寻找非0,接下来移动。不过不一定正确……
int j=1,k=0;
while (m[j]) j++;
if (j==8) continue;
k=j+1;
while (m[k]==0 && k<8) k++;
while (k<8) swap(m[j++],m[k++]);
}
}
// 检查是否可以消除方块。如果可以,就消除方块。
bool mark[6][8]; // 消除方块时用
bool check(int depth)
{
bool changed=false;
memset(mark,0,sizeof(mark));
// 检查是否可以消除
// 水平方向
for (int i=1; i<=5; i++)
for (int delta=7; delta>=3; delta--) // 连通的方块数
for (int j=1; j<=8-delta; j++)
{
int a=map[depth][i][j];
for (int k=j+1; k<=j+delta-1; k++)
if (map[depth][i][k]!=a)
{
a=0;
break;
}
if (a) for (int k=j; k<=j+delta-1; k++) mark[i][k]=true;
}
// 竖直方向
for (int j=1; j<=7; j++)
for (int delta=5; delta>=3; delta--)
for (int i=1; i<=6-delta; i++)
{
int a=map[depth][i][j];
for (int k=i+1; k<=i+delta-1; k++)
if (map[depth][k][j]!=a)
{
a=0;
break;
}
if (a) for (int k=i; k<=i+delta-1; k++) mark[k][j]=true;
}
// 消除
for (int i=1; i<=5; i++)
for (int j=1; j<=7; j++)
if (mark[i][j]) map[depth][i][j]=0, changed=true;
return changed;
}
// 进行搜索,如果有解则返回true,否则返回false。
bool DFS(int depth)
{
if (depth>n)
{
for (int i=1; i<=5; i++)
if (map[n+1][i][1]) return false;
return true;
}
for (int i=1; i<=5; i++)
for (int j=1; j<=7; j++)
{
/*
移动一种方块。分四种情况:
① 方块本身就是0,那么直接跳过;
② 在左边界,只能向右移动;
③ 在右边界,只能向左移动。如果左边有方块,那么可以忽略这一步,
因为那个方块右移和这个方块左移效果相同,但字典序更小。
也就是说,在右边界时,如果左边为空,则向左移动,否则不移动。
④ 不在边界,如果左边为空,就既向左又向右(特殊考虑,因为要多一段代码);
如果左边不为空,那么不管右边是什么都向右移动。
*/
if (map[depth][i][j]==0) continue;
a[depth]=i;
b[depth]=j;
int &dir=c[depth]; // 移动方向
if (i<5) // 第②种情况+第④种情况的第一部分
dir=1;
else if (i==5 && map[depth][4][j]==0) // 第③种情况
dir=-1;
else
continue;
memcpy(map[depth+1], map[depth], sizeof(map[depth]));
swap(map[depth+1][i][j], map[depth+1][i+dir][j]);
// 下落与消除方块
do
{
fall(depth+1);
} while (check(depth+1));
// 继续搜索
if (DFS(depth+1)) return true;
if (i>1 && i<5 && map[depth][i-1][j]==0) // 第④种情况的第二部分
{
a[depth]=i;
b[depth]=j;
dir=-1;
memcpy(map[depth+1], map[depth], sizeof(map[depth]));
swap(map[depth+1][i][j], map[depth+1][i+dir][j]);
// 和上面一样
do
{
fall(depth+1);
} while (check(depth+1));
if (DFS(depth+1)) return true;
}
}
return false;
}
int main()
{
memset(map,0,sizeof(map));
cin>>n;
for (int i=1; i<=5; i++)
{
int temp, j=1;
do
{
cin>>temp;
map[1][i][j++]=temp;
} while (temp);
}
if (DFS(1))
for (int i=1; i<=n; i++)
cout<<(a[i]-1)<<" "<<(b[i]-1)<<" "<<c[i]<<endl;
else
cout<<"-1"<<endl;
return 0;
}这都4000多字了~~~