【贝叶斯决策理论】— 基于两类问题的决策分析
在jupyter lab上实现:

导包:
import numpy as np
from numpy.linalg import cholesky
import matplotlib.pyplot as plt
设置随机样本数:
sampleNo = 40;
第一类:
# w1
mu = np.array([[2, 2]])
Sigma = np.array([[2, 0], [0, 2]])
R = cholesky(Sigma)
s = np.dot(np.random.randn(sampleNo, 2), R) + mu
plt.plot(s[:,0],s[:,1],'r+')
plt.title('$w_1$')
plt.show()
图示:
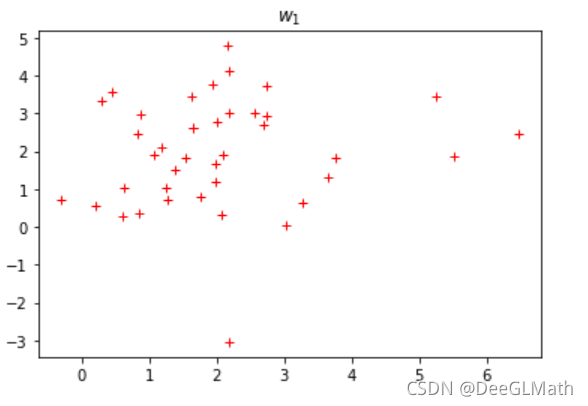
第二类:
# w2
mu = np.array([[4, 4]])
Sigma = np.array([[1, 0], [0, 1]])
R = cholesky(Sigma)
s = np.dot(np.random.randn(sampleNo, 2), R) + mu
plt.plot(s[:,0],s[:,1],'r+')
plt.title('$w_2$')
plt.show()
图示:
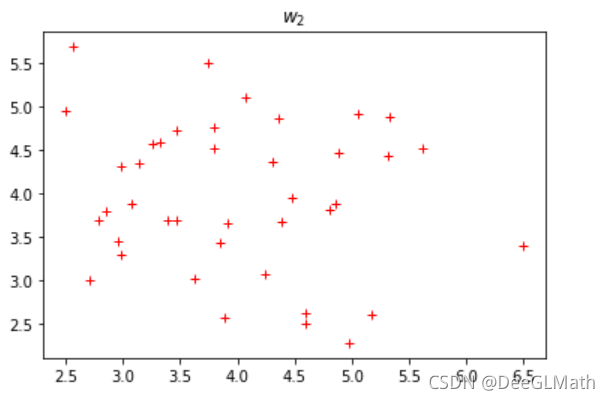
两类判别函数的一般式:
g
i
(
x
)
=
−
1
2
σ
i
2
(
x
1
2
+
x
2
2
)
+
1
σ
i
2
(
μ
i
1
x
1
+
μ
i
2
x
2
)
−
1
2
σ
i
2
(
μ
i
1
2
+
μ
i
2
2
)
+
ln
P
(
w
i
)
−
d
2
ln
2
π
−
1
2
ln
∣
Σ
i
∣
g_i(x)=-\frac{1}{2 \sigma_i^2} (x_1^2+x_2^2) + \frac{1}{\sigma_i^2} (\mu_{i1} x_1 + \mu_{i2} x_2) - \frac{1}{2 \sigma_i^2} (\mu_{i1}^2+\mu_{i2}^2) + \ln P(w_i) -\frac{d}{2} \ln 2\pi-\frac{1}{2} \ln |\Sigma_i|
gi(x)=−2σi21(x12+x22)+σi21(μi1x1+μi2x2)−2σi21(μi12+μi22)+lnP(wi)−2dln2π−21ln∣Σi∣
说明:
σ
1
2
=
2
,
σ
2
2
=
1
μ
1
=
[
2
,
2
]
T
,
μ
2
=
[
4
,
4
]
T
P
(
w
1
)
=
P
(
w
2
)
=
1
2
d
=
2
∣
Σ
1
∣
=
4
,
∣
Σ
2
∣
=
1
\sigma_1^2=2,\sigma_2^2=1 \\ \mu_1=[2,2]^T,\mu_2=[4,4]^T \\ P(w_1)=P(w_2)=\frac{1}{2} \\ d=2 \\ |\Sigma_1|=4,|\Sigma_2|=1
σ12=2,σ22=1μ1=[2,2]T,μ2=[4,4]TP(w1)=P(w2)=21d=2∣Σ1∣=4,∣Σ2∣=1
g
1
(
x
)
g_1(x)
g1(x):
g
1
(
x
)
=
−
1
4
(
x
1
2
+
x
2
2
)
+
x
1
+
x
2
−
2
−
2
ln
2
−
ln
2
π
g_1(x)=-\frac{1}{4} (x_1^2+x_2^2) + x_1 + x_2 - 2 - 2\ln 2 - \ln 2 \pi
g1(x)=−41(x12+x22)+x1+x2−2−2ln2−ln2π
g
2
(
x
)
g_2(x)
g2(x):
g
1
(
x
)
=
−
1
2
(
x
1
2
+
x
2
2
)
+
4
x
1
+
4
x
2
−
8
−
ln
2
−
ln
2
π
g_1(x)=-\frac{1}{2} (x_1^2+x_2^2) + 4x_1 + 4x_2 - 8 - \ln 2 - \ln 2 \pi
g1(x)=−21(x12+x22)+4x1+4x2−8−ln2−ln2π
g
1
(
x
)
−
g
2
(
x
)
g_1(x)-g_2(x)
g1(x)−g2(x):
g
1
(
x
)
−
g
2
(
x
)
=
1
4
(
x
1
2
+
x
2
2
)
−
3
x
1
−
3
x
2
+
6
−
ln
2
g_1(x)-g_2(x)=\frac{1}{4} (x_1^2+x_2^2) - 3x_1 - 3x_2 + 6 - \ln 2
g1(x)−g2(x)=41(x12+x22)−3x1−3x2+6−ln2
判别界面的方程:
1
4
(
x
1
2
+
x
2
2
)
−
3
x
1
−
3
x
2
+
6
−
ln
2
=
0
\frac{1}{4} (x_1^2+x_2^2) - 3x_1 - 3x_2 + 6 - \ln 2 = 0
41(x12+x22)−3x1−3x2+6−ln2=0
判别界面图像绘制代码:
from sympy.parsing.sympy_parser import parse_expr
from sympy import plot_implicit
ezplot = lambda exper: plot_implicit(parse_expr(exper)) # 用了匿名函数
expression='0.25*(x**2+y**2)-3*x-3*y+6-log(2)'
ezplot(expression); # 能描绘大致的图像
图示:
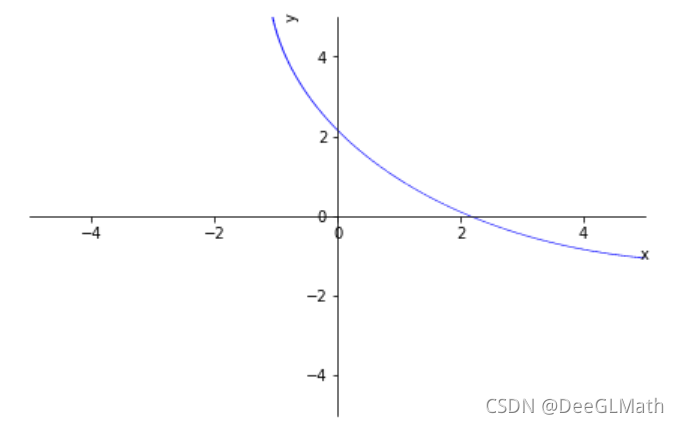
曲线下方为 w 1 w_1 w1,曲线上方为 w 2 w_2 w2

第一类:
sampleNo = 50; % 随机样本数
mu = np.array([[0, 0, 0]])
Sigma = np.array([[0.3, 0, 0], [0, 0.3, 0],[0, 0, 0.3]])
R = cholesky(Sigma)
s = np.dot(np.random.randn(sampleNo, 3), R) + mu
x, y, z = s[:,0],s[:,1],s[:,2]
ax = plt.subplot(111, projection='3d') # 创建一个三维的绘图工程
ax.scatter(x, y, z, c='r')
plt.title('$w_1$')
ax.set_zlabel('Z')
ax.set_ylabel('Y')
ax.set_xlabel('X')
plt.show()
图示:
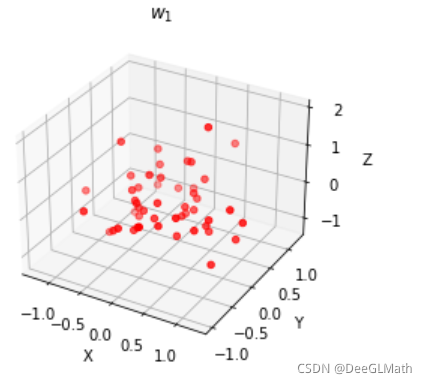
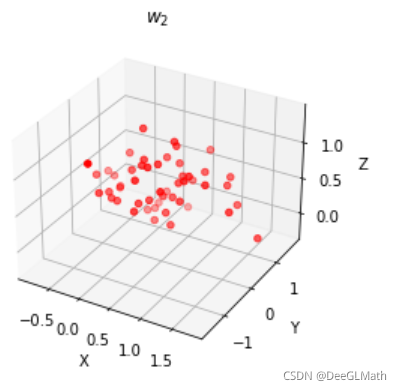
第二类:
sampleNo = 50;
mu = np.array([[0.5, 0.5, 0.5]])
Sigma = np.array([[0.3, 0.1, 0.1], [0.1, 0.3, -0.1],[0.1, -0.1, 0.3]])
R = cholesky(Sigma)
s = np.dot(np.random.randn(sampleNo, 3), R) + mu
x, y, z = s[:,0],s[:,1],s[:,2]
ax = plt.subplot(111, projection='3d') # 创建一个三维的绘图工程
ax.scatter(x, y, z, c='r')
plt.title('$w_2$')
ax.set_zlabel('Z')
ax.set_ylabel('Y')
ax.set_xlabel('X')
plt.show()
图示:
判别函数一般式:
g
i
(
x
)
=
−
1
2
x
T
Σ
i
−
1
x
+
1
2
x
T
Σ
i
−
1
μ
i
−
1
2
μ
i
T
Σ
i
−
1
μ
i
+
1
2
μ
i
T
Σ
i
−
1
x
+
ln
P
(
w
i
)
−
(
d
/
2
)
ln
2
π
−
(
1
/
2
)
ln
∣
Σ
i
∣
g_i(x)=-\frac{1}{2} x^T \Sigma_i^{-1} x+\frac{1}{2} x^T \Sigma_i^{-1} \mu_i - \frac{1}{2} \mu_i^T \Sigma_i^{-1} \mu_i + \frac{1}{2} \mu_i^T \Sigma_i^{-1} x + \ln P(w_i) -(d/2)\ln 2\pi-(1/2) \ln |\Sigma_i|
gi(x)=−21xTΣi−1x+21xTΣi−1μi−21μiTΣi−1μi+21μiTΣi−1x+lnP(wi)−(d/2)ln2π−(1/2)ln∣Σi∣
g
1
(
x
)
g_1(x)
g1(x):
g
1
(
x
)
=
−
5
3
(
x
1
2
+
x
2
2
+
x
3
2
)
−
ln
2
−
3
2
ln
2
π
+
1.8060
g_1(x)=-\frac{5}{3} (x_1^2+x_2^2+x_3^2) - \ln 2 -\frac{3}{2} \ln 2\pi+1.8060
g1(x)=−35(x12+x22+x32)−ln2−23ln2π+1.8060
g
2
(
x
)
g_2(x)
g2(x):
g
2
(
x
)
=
0.3
(
x
1
2
+
x
2
2
+
x
3
2
)
+
0.2
(
x
1
x
2
+
x
1
x
3
−
x
2
x
3
)
−
0.5
x
1
−
0.3
x
2
−
0.3
x
3
−
ln
2
−
3
2
ln
2
π
+
2.0676
g_2(x)=0.3(x_1^2+x_2^2+x_3^2)+0.2(x_1x_2+x_1x_3-x_2x_3)-0.5x_1-0.3x_2-0.3x_3- \ln 2 -\frac{3}{2} \ln 2\pi +2.0676
g2(x)=0.3(x12+x22+x32)+0.2(x1x2+x1x3−x2x3)−0.5x1−0.3x2−0.3x3−ln2−23ln2π+2.0676
g
1
(
x
)
−
g
2
(
x
)
g_1(x)-g_2(x)
g1(x)−g2(x):
g
1
(
x
)
−
g
2
(
x
)
=
−
59
30
(
x
1
2
+
x
2
2
+
x
3
2
)
−
0.2
(
x
1
x
2
+
x
1
x
3
−
x
2
x
3
)
+
0.5
x
1
+
0.3
x
2
+
0.3
x
3
−
0.2616
g_1(x)-g_2(x)=-\frac{59}{30}(x_1^2+x_2^2+x_3^2)-0.2(x_1x_2+x_1x_3-x_2x_3) +0.5x_1+0.3x_2+0.3x_3 -0.2616
g1(x)−g2(x)=−3059(x12+x22+x32)−0.2(x1x2+x1x3−x2x3)+0.5x1+0.3x2+0.3x3−0.2616
决策面方程:
−
59
30
(
x
1
2
+
x
2
2
+
x
3
2
)
−
0.2
(
x
1
x
2
+
x
1
x
3
−
x
2
x
3
)
+
0.5
x
1
+
0.3
x
2
+
0.3
x
3
−
0.2616
=
0
-\frac{59}{30}(x_1^2+x_2^2+x_3^2)-0.2(x_1x_2+x_1x_3-x_2x_3) +0.5x_1+0.3x_2+0.3x_3 -0.2616=0
−3059(x12+x22+x32)−0.2(x1x2+x1x3−x2x3)+0.5x1+0.3x2+0.3x3−0.2616=0