目录
1. 问题描述
2. 解题分析
2.1 如何判断能否铺
2.2 状态表示和遍历
2.3 围栏
3. 代码及测试
4. 后记
1. 问题描述
考虑叫做“仪式铺法”的榻榻米铺法,这种铺法可以使相邻榻榻米之间的接缝不会形成十字,象征着吉祥。举个例子,如果一个房间看作由纵3*横4个正方形方格构成,铺满这个房间需要6张榻榻米(榻榻米的大小是统一的1*2的长方形),则铺法如下所示(还有与这两个成上下或左右对称的图案此处略去):
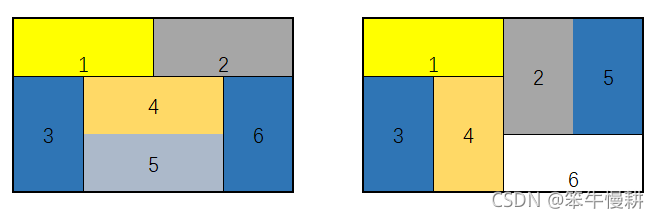
图1 (3,4)的房间的两种铺法
求用14张榻榻米铺满大小为4*7的房间的铺法。
2. 解题分析
深度优先路径遍历问题。
这一类问题的难点主要体现在(具体问题的形式千差万别)如何将问题转换为易于遍历搜索的问题表述形式,或者如何找到有效的遍历方式(包括节点状态表示,以及如何确定邻节点或者说子节点)。
2.1 如何判断能否铺
经过分析可以发现,构成非法铺法的一个关键特征是在某一个点的周围4个块均属于4块不同的榻榻米。如下图所示两个都是NG的铺法。
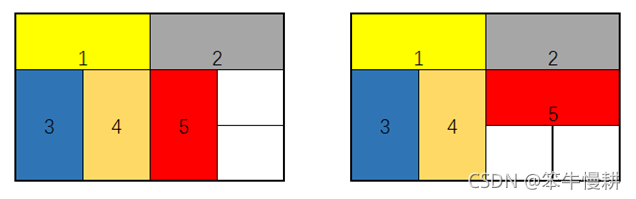
图2 非法的铺法例
那如何把这种约束条件转化为容易判别的形式(换句话说人眼识别以上NG图案很容易,如何让计算机能做出判断)呢?比如说,如下图的状态,现在要判断带问号“?”的格子是否可以铺下一张榻榻米(无论是纵还是横?)
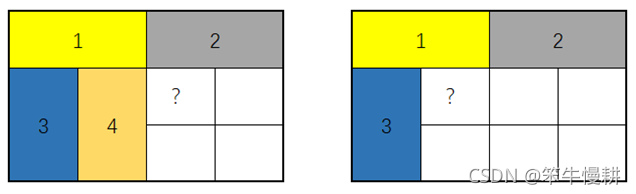
图3 “?”格子能够铺?
如前所述,非法的铺法中是指在某个交点周围的4个格子分属于不同的榻榻米。所以在判断“?”处是否能铺,作为充要条件(这里先不考虑触及边界的情况)就是判断“左上、上、左”这个三个格子是否不全部属于不同的榻榻米。换言之,只要“左上、上”属于同一榻榻米、或者“上、左”属于同一榻榻米即表明当前格子可以铺新的榻榻米(“左上、左”肯定分属不同的榻榻米不必判断)。反之,如果“左上、上”属于不同榻榻米、且“上、左”属于不同榻榻米则表明当前格子肯定不能铺。据此可以判断,上图中,左边不能铺,右边可以铺。
这也就自然地引出了给到当前状态为止已经铺好的榻榻米进行编号的考虑,以方便进行以上判断。
2.2 状态表示和遍历
【有点复杂的想法】
以整个房间的铺设状态作为图的节点,可以表示为H*W的矩阵(H为纵向高度,W为横向宽度),矩阵元素取值{0:尚未覆盖;非零IDX:已经序号IDX的榻榻米被覆盖}。起始状态(即深度优先搜索树的根节点)为全0状态。终止状态为全非零状态。这样这个问题就转变成在一张图中搜索从某个节点(全‘0’状态)出发,到达另一个节点(全非零状态)的所有路径的问题。
然后,邻节点搜索可以这样考虑,遍历与移近覆盖的区域相邻(有共同的边)的格子,检查从各邻接格子是否能够铺设(因为是从左上往右下搜索的方式,针对每个格子只需要考虑向右铺或向下铺)。这种方法的好处是递归深度会小一些,但是已覆盖区域的邻接格子的查询似乎比较麻烦。
【逐行扫描】
原书中给出的解法(这道题原书给出的Javascript代码比ruby容易理解些好歹看懂了)很巧妙(当然要自己先撞墙了然后再读懂了才能体会其中妙处并感叹我怎么没想到)。
简单地逐行(当然逐列也可以)逐格扫描过去,碰到边界就切换到下一行,碰到已经被覆盖的就跳过去,针对既非越界也没有被覆盖的格子结合当前已经铺就的状态进行是否能铺(参见上一节的描述)的判断。加上“围栏”技巧(参见下一节)以及给榻榻米编号的技巧,得到了一个非常简洁的实现。
这一解法的缺点可能是递归深度相对来说会比较大,当问题规模比较大的时候容易触及递归深度限制(有待确认)
以下为(H=3,W=4)的递归搜索示意图(没有画出围栏,可以把格点坐标按照matlab-style的从1开始的方式理解;黑点表示当前探索的格子,旁边(x,y,idx)对应的递归调用的参数)
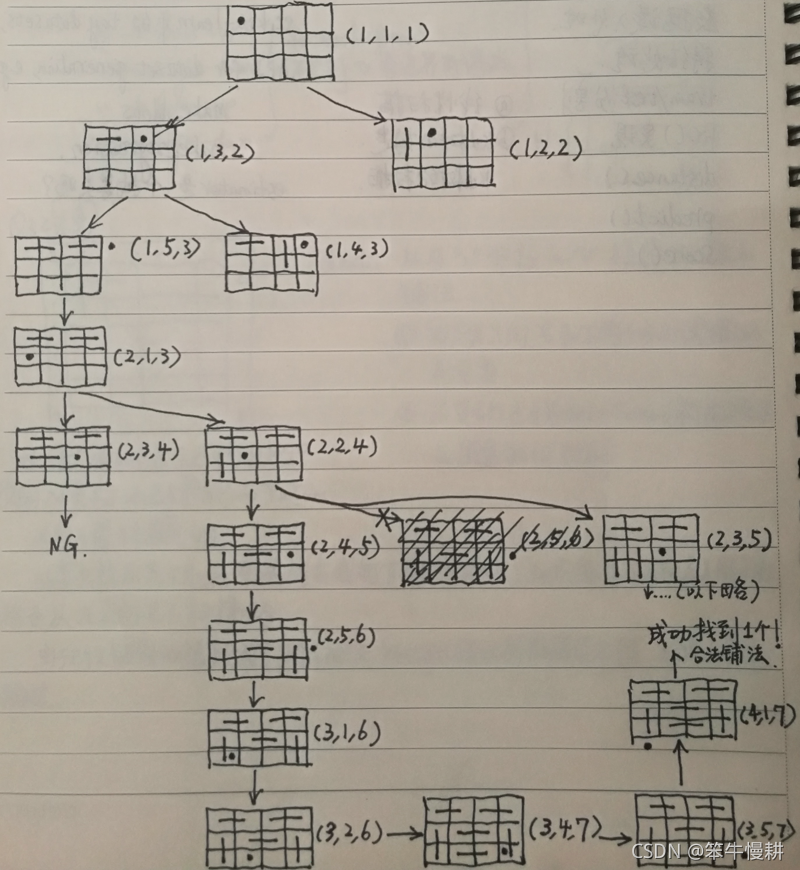
2.3 围栏
如原书中所述,对于棋盘类问题,很多时候,在问题界定的范围外侧加上围栏就可以简化边界条件的判定。在本题解中,在H*W格子矩阵外围追加一圈格子,并全部赋值为“-1”。在代码中虽然没有显式地(explicitly)用到“-1”的判断,但是在“if room[h,w+1]==0:”和“if room[h+1,w]==0:”判断中隐式地(implicitly)利用到了。因为追加了外围的一层,所以不必担心(w+1)和(h+1)越界而导致矩阵访问出错;另外,由于初始化为“-1”,所以在上述判断不会被误判为有效的可填的格子。
3. 代码及测试
以下代码是参照原书的“逐行扫描”策略的解法,改为“逐列扫描”也可以。另外,也没有特意地写一个打印出铺好的图案的函数--相对来说是一个比较trivial的事情。从打印出来的table应该很容易描画出铺好的图案来。
# -*- coding: utf-8 -*-
"""
Created on Thu Sep 16 07:18:04 2021
@author: chenxy
"""
import sys
import time
import datetime
import math
# import random
from typing import List
# from queue import Queue
# from collections import deque
import itertools as it
import numpy as np
H = 4 # Heigth of the room
W = 7 # Weigth of the room
# room initialization, with a guard band surrounding the original room
# The guard band is initialized to '-1' to simplify the judgement processing.
room = np.zeros((H+2, W+2))
room[0,:] = -1
room[H+1,:] = -1
room[:,0] = -1
room[:,W+1] = -1
count = 0
def setTatami_rowscan(h,w,idx)->int:
'''
Parameters
----------
(h,w) : The current exploration point. h represents row number, w represents col number.
idx : The identifier index of Tatami to be arranged.
Returns: int
The number of total arrangement from the input condition.
'''
global count
# print(h,w,idx)
if h == H + 1:
count = count + 1
print(room)
elif w == W + 1:
# Reach the right boundary, go to explore the next row from the left
setTatami_rowscan(h+1, 1, idx)
elif room[h,w] > 0:
# This grid has been occupied, move to the right one
setTatami_rowscan(h, w+1, idx)
elif room[h-1,w]==room[h-1,w-1] or room[h,w-1]==room[h-1,w-1]:
# if (the same IDX for up and left-up) or (the same IDX for left and left-up),
# Tatami arrangement is allowed.
if room[h,w+1]==0:
# Horizontal arrangement is allowed
room[h,w] = idx
room[h,w+1] = idx
setTatami_rowscan(h, w+2, idx+1)
room[h,w] = 0
room[h,w+1] = 0
if room[h+1,w]==0:
# Vertical arrangement is allowed
room[h,w] = idx
room[h+1,w] = idx
setTatami_rowscan(h, w+1, idx+1)
room[h,w] = 0
room[h+1,w] = 0
tStart = time.perf_counter()
setTatami_rowscan(1, 1, 1)
tCost = time.perf_counter() - tStart
print('count = {0}, tCost = {1:6.3f}(sec)'.format(count,tCost))
运行结果(H=4, W=7):
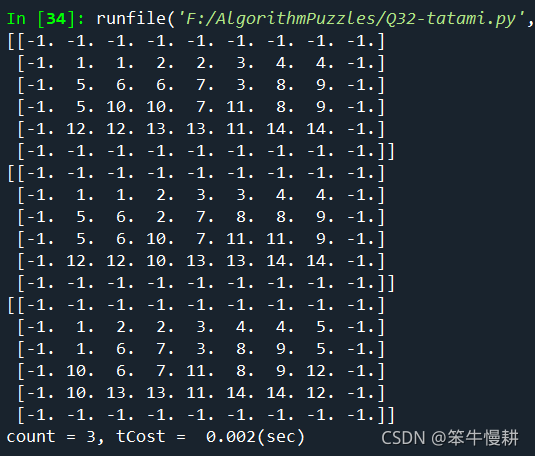
4. 后记
后面要回头再把第一种【有点复杂的想法】也实现一下,并比较一下前面的关于当前实现方式会导致更深的递归深度的问题是否存在。
上一篇:Q31: 计算最短路径
下一篇:Q33: 飞车与角行的棋步
本系列总目录参见:程序员的算法趣题:详细分析和Python全解