前言

这一篇文章，我会详细介绍如何利用Python来实现线性回归以及线性回归的实战模拟，以及回归模型的评估指标的详细介绍，感兴趣的朋友可以看一看。

1 线性回归的Scikit-learn实现

接下来以一个加利福尼亚的房价预测为案例进行讲解实现。

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.datasets import fetch_california_housing #加利福尼亚房屋价值数据集
import pandas as pd 

1.1 导入模块后开始下载数据

housevalue = fetch_california_housing() 

housevalue

housevalue.feature_names
# 特征解释
# MedInc：该街区住户的收入中位数
# HouseAge：该街区房屋使用年代的中位数
# AveRooms：该街区平均的房间数目
# AveBedrms：该街区平均的卧室数目
# Population：街区人口
# AveOccup：平均入住率
# Latitude：街区的纬度
# Longitude：街区的经度

将数据转成DataFrame：

X = pd.DataFrame(housevalue.data,columns=housevalue.feature_names)
X

y = housevalue.target
y

1.2 拆分数据集（训练集和测试集）

Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size=0.3,random_state=420)

1.3 线性回归建模

lr = LinearRegression()

1.4 训练数据

lr.fit(Xtrain,Ytrain)

1.5 模型评估

接下来进行模型评估，这里的评估指标有很多，我们先从MSE均方误差开始介绍。

MSE均方误差

• MSE趋于0效果越好

from sklearn.metrics import mean_squared_error

#对训练集做预测
y_pred =lr.predict(Xtrain)#得到预测结果

# 评估训练集集合情况  参数1:真实标签 参数2:预测标签
mean_squared_error(Ytrain,y_pred)

0.52185226625331

y_test_pred = lr.predict(Xtest)
mean_squared_error(Ytest,y_test_pred)

0.5309012639324568

注意，这个MSE值是越小越趋于0越好，在这里MSE为0.53其实不是很好，当然还要结合其他指标评估。

交叉验证

lr2 = LinearRegression()

# 交叉验证使用-MSE指标
cross_val_score(lr2,Xtrain,Ytrain,cv=10,scoring='neg_mean_squared_error')

array([-0.52730876, -0.50816696, -0.48736401, -0.49269076, -0.56611205,
-0.53795641, -0.48253409, -0.5130032 , -0.53188562, -0.60443733])

注意这里的指标前面是有neg_的，不要忘了，不能会报错。同时结果是负数也不影响你的判断。

当然，如果你想知道里面指标都有哪些，可以用到下列方法：

import sklearn
sorted(sklearn.metrics.SCORERS.keys())

接下来看下交叉验证的平均值：

cross_val_score(lr2,Xtrain,Ytrain,cv=10,scoring='neg_mean_squared_error').mean()

-0.525145918217335

MAE绝对均值误差

当然啦，除了MSE，还可以用MAE作为评估指标。MAE与MSE差不多，两个选一个用即可。

from sklearn.metrics import mean_absolute_error

mean_absolute_error(Ytrain,y_pred) 

# 交叉验证使用-MAE指标
cross_val_score(lr2,Xtrain,Ytrain,cv=10,scoring='neg_mean_absolute_error')

cross_val_score(lr2,Xtrain,Ytrain,cv=10,scoring='neg_mean_absolute_error').mean()

-0.5313931576388832

R方

• 方差是来衡量数据集包含了多少信息量（数据都是0和数据从1到1000都有，很明显是后者信息量大）
• R方越趋于1拟合效果就越好，趋于0拟合效果越差
• R方是回归模型最常用的评估指标。

from sklearn.metrics import r2_score

r2_score(Ytrain,y_pred) #训练集R2

0.6067440341875014

r2_score(Ytest,y_test_pred) #测试集R2

0.6043668160178819

或者可以直接这样：

lr.score(Xtrain,Ytrain)

0.6067440341875014

lr.score(Xtest,Ytest)

0.6043668160178819

细心的朋友应该可以看到上面的数据是跟下面的数据是一样的，因为这里的lr.score()默认使用的指标就是R方。

同样这里也可以用交叉验证：

cross_val_score(lr,Xtrain,Ytrain,cv=10,scoring='r2')

cross_val_score(lr,Xtrain,Ytrain,cv=10,scoring='r2').mean()

0.603923823554634

查看模型系数

lr.coef_ #训练结果

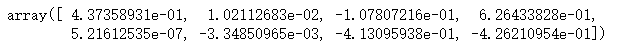
lr.intercept_ # 截距

-36.25689322920392

list(zip(X.columns,lr.coef_))

这里也就是我们求的系数，也就是 w w w。

1.6 将数据集标准化之后再训练

from sklearn.preprocessing import StandardScaler

std = StandardScaler()

#对训练集进行标准化
X_train_std = std.fit_transform(Xtrain)
X_train_std

我们再看一下之前的数据：

Xtrain

区别还是很大的。

接下来用标准化的数据来训练。

lr3 = LinearRegression()

lr3.fit(X_train_std,Ytrain)

lr3.score(X_train_std,Ytrain)

0.6067440341875014

稍微起了一点点作用（因为各数据之间的差异性不是很大）。

1.7 绘制拟合图像

• 绘制预测值的散点和真实值的直线进行对比
• 如果两者趋势越接近（预测值的散点越靠近真实值）拟合效果优秀

# 因为数据是无序的，所以画出的点是乱的
plt.scatter(range(len(Ytest)),Ytest,s=2)
plt.show()

那怎么办呢？

我们可以给它排个序。

plt.scatter(range(len(Ytest)),sorted(Ytest),s=2)
plt.show()

那为了让预测值和真实值能一一对应，应该用如下方法：

y_test_pred[np.argsort(Ytest)]

将排序好的数据再进行绘图

plt.scatter(range(len(Ytest)),sorted(Ytest),s=2,label='True')
plt.scatter(range(len(Ytest)),y_test_pred[np.argsort(Ytest)],s=2,c='r',label='Predict',alpha=0.3)  # 这里的alpha是用来调整点透明度的

plt.legend()
plt.show()

总体看起来还可以，但是可以发现后面的数据明显有些预测得不好。

2 多重共线性

2.1 理解与代码实现

上文我们也说了，在线性回归当中不能存在多重共线性，为什么呢？

这里先回到我们上文：
这里可解的前提是矩阵的逆是存在的，而为什么不能存在多重共线性正是因为这样的话逆会不存在。

我们回想一下逆矩阵的计算公式： A − 1 = 1 ∣ A ∣ A ∗ A^{-1}=\frac{1}{|A|}A^* A−1=∣A∣1​A∗其中这个 A ∗ A^* A∗是伴随矩阵，而任何矩阵都可以有伴随矩阵，所以这个并不影响逆矩阵的存在，所以关键在于 ∣ A ∣ |A| ∣A∣， ∣ A ∣ |A| ∣A∣是矩阵 A A A的行列式，并且它还在分母上，这就意味着它要是等于0，那么就不存在逆矩阵了。

我们看一下下面这张图：

这是三个矩阵进行了一些初等行变换，转换成了梯形矩阵（转换往往是为了机器方便后续计算），而矩阵 A A A最终转换出现了零行，而矩阵 B B B第三行也接近零行了，只有第三行较为正常。

熟悉行列式计算的朋友们应该能想起来 A A A的值等于0，而矩阵 B B B是接近为0，这会导致什么结果？这样会导致 A A A的 1 ∣ A ∣ \frac{1}{|A|} ∣A∣1​不存在，而 B B B的 1 ∣ A ∣ \frac{1}{|A|} ∣A∣1​接近于无穷大（分母越小越趋于无穷大），这些都是我们不希望看到的。

矩阵A中第一行和第三行的关系，被称为“精确相关关系”，即完全相关，一行可使另一行为0。矩阵B则属于非常接近于”精确相关关系“，但又不是完全相关，这种关系被称为”高度相关关系“。在这种情况下，最小二乘法可以使用，不过得到的逆会很大，直接影响我们对w参数向量的求解。

所以到这里，朋友们应该知道为什么线性回归不能存在多重共线性了吧。

那值得一提的是，多重共线性如果存在，则线性回归就无法使用最小二乘法来进行求解，或者求解就会出现偏差。幸运的是，不能存在多重共线性，不代表不能存在相关性——机器学习不要求特征之间必须独立，必须不相关，只要不是高度相关或者精确相关就好。多重共线性是一种统计现象，是指线性模型中的特征(解释变量)之间由于存在精确相关关系或高度相关关系，多重共线性的存在会使模型无法建立，或者估计失真。 多重共线性使用指标方差膨胀因子(variance inflation factor，VIF)来进行衡量，通常当我们提到“共线性”，都特指多重共线性。相关性是衡量两个或多个变量一起波动的程度的指标，它可以是正的，负的或者0。 当我们说变量之间具有相关性，通常是指线性相关性。

划重点： 在现实中特征之间完全独立的情况其实非常少，因为大部分数据统计手段或者收集者并不考虑统计学或者机器学习建模时的需求，现实数据多多少少都会存在一些相关性，极端情况下，甚至还可能出现收集的特征数量比样本数量多的情况。通常来说，这些相关性在机器学习中通常无伤大雅(在统计学中他们可能是比较严重的问题)，即便有一些偏差，只要最小二乘法能够求解，我们都有可能会无视掉它。毕竟，想要消除特征的相关性，无论使用怎样的手段，都无法避免进行特征选择，这意味着可用的信息变得更加少，对于机器学习来说，很有可能尽量排除相关性后，模型的整体效果会受到巨大的打击。这种情况下，我们选择不处理相关性，只要结果好，一切万事大吉。然而多重共线性就不是这样一回事了，它的存在会造成模型极大地偏移，无法模拟数据的全貌，因此这是必须解决的问题。

那接下来我们来看看多重共线性在我们代码中是如何解决的吧？

X.columns = ['住户的收入中位数','房屋使用年代的中位数','该街区平均的房间数目',
             '该街区平均的卧室数目','街区人口','平均入住率','街区的纬度','街区的经度']

# 先把列名都变成中文的，方便观察。

我们可以通过多项式把这些列构建出来。

首先把包导进来：

from sklearn.preprocessing import PolynomialFeatures

进行实例化（这就是多项式转化的对象）

poly = PolynomialFeatures(degree=2).fit(X,y) 
# 这里的degree设置过大电脑会很卡的，2 3 4就差不多了

poly.get_feature_names(X.columns)#通过多项式构造列

[‘1’,
‘住户的收入中位数’,
‘房屋使用年代的中位数’,
‘该街区平均的房间数目’,
‘该街区平均的卧室数目’,
‘街区人口’,
‘平均入住率’,
‘街区的纬度’,
‘街区的经度’,
‘住户的收入中位数^2’,
‘住户的收入中位数 房屋使用年代的中位数’,
‘住户的收入中位数 该街区平均的房间数目’,
‘住户的收入中位数 该街区平均的卧室数目’,
‘住户的收入中位数 街区人口’,
‘住户的收入中位数 平均入住率’,
‘住户的收入中位数 街区的纬度’,
‘住户的收入中位数 街区的经度’,
‘房屋使用年代的中位数^2’,
‘房屋使用年代的中位数 该街区平均的房间数目’,
‘房屋使用年代的中位数 该街区平均的卧室数目’,
‘房屋使用年代的中位数 街区人口’,
‘房屋使用年代的中位数 平均入住率’,
‘房屋使用年代的中位数 街区的纬度’,
‘房屋使用年代的中位数 街区的经度’,
‘该街区平均的房间数目^2’,
‘该街区平均的房间数目 该街区平均的卧室数目’,
‘该街区平均的房间数目 街区人口’,
‘该街区平均的房间数目 平均入住率’,
‘该街区平均的房间数目 街区的纬度’,
‘该街区平均的房间数目 街区的经度’,
‘该街区平均的卧室数目^2’,
‘该街区平均的卧室数目 街区人口’,
‘该街区平均的卧室数目 平均入住率’,
‘该街区平均的卧室数目 街区的纬度’,
‘该街区平均的卧室数目 街区的经度’,
‘街区人口^2’,
‘街区人口 平均入住率’,
‘街区人口 街区的纬度’,
‘街区人口 街区的经度’,
‘平均入住率^2’,
‘平均入住率 街区的纬度’,
‘平均入住率 街区的经度’,
‘街区的纬度^2’,
‘街区的纬度 街区的经度’,
‘街区的经度^2’]

X_ = poly.transform(X)  #多项式变化后
X_

reg = LinearRegression().fit(X_,y)#使用转化后的数据进行建模训练

reg.coef_

[*zip(poly.get_feature_names(X.columns),reg.coef_)]

[(‘1’, 5.919547622013033e-08),
(‘住户的收入中位数’, -11.24302557462409),
(‘房屋使用年代的中位数’, -0.8488985630544302),
(‘该街区平均的房间数目’, 6.441059285824681),
(‘该街区平均的卧室数目’, -31.59133038837795),
(‘街区人口’, 0.0004060907004548096),
(‘平均入住率’, 1.0038623267368598),
(‘街区的纬度’, 8.705681906512265),
(‘街区的经度’, 5.880632740950536),
(‘住户的收入中位数^2’, -0.031308123295653814),
(‘住户的收入中位数 房屋使用年代的中位数’, 0.0018599473971959836),
(‘住户的收入中位数 该街区平均的房间数目’, 0.04330204720647667),
(‘住户的收入中位数 该街区平均的卧室数目’, -0.18614230286022418),
(‘住户的收入中位数 街区人口’, 5.728313132329231e-05),
(‘住户的收入中位数 平均入住率’, -0.002590194649331616),
(‘住户的收入中位数 街区的纬度’, -0.15250571828258908),
(‘住户的收入中位数 街区的经度’, -0.14424294425079082),
(‘房屋使用年代的中位数^2’, 0.00021172532576618083),
(‘房屋使用年代的中位数 该街区平均的房间数目’, -0.0012621899769862225),
(‘房屋使用年代的中位数 该街区平均的卧室数目’, 0.010611505200531843),
(‘房屋使用年代的中位数 街区人口’, 2.818853379960247e-06),
(‘房屋使用年代的中位数 平均入住率’, -0.0018171694411520457),
(‘房屋使用年代的中位数 街区的纬度’, -0.010069037338454228),
(‘房屋使用年代的中位数 街区的经度’, -0.00999950188065276),
(‘该街区平均的房间数目^2’, 0.007269477252714056),
(‘该街区平均的房间数目 该街区平均的卧室数目’, -0.0689064336889457),
(‘该街区平均的房间数目 街区人口’, -6.823655839335575e-05),
(‘该街区平均的房间数目 平均入住率’, 0.02688788388649532),
(‘该街区平均的房间数目 街区的纬度’, 0.08750899386040001),
(‘该街区平均的房间数目 街区的经度’, 0.08228903893629276),
(‘该街区平均的卧室数目^2’, 0.1601809459853239),
(‘该街区平均的卧室数目 街区人口’, 0.0005142639649729885),
(‘该街区平均的卧室数目 平均入住率’, -0.08719113908251339),
(‘该街区平均的卧室数目 街区的纬度’, -0.4370430295730081),
(‘该街区平均的卧室数目 街区的经度’, -0.4041506064429531),
(‘街区人口^2’, 2.737790919310526e-09),
(‘街区人口 平均入住率’, 1.9142676560849866e-05),
(‘街区人口 街区的纬度’, 2.2952983608247036e-05),
(‘街区人口 街区的经度’, 1.4656775581091295e-05),
(‘平均入住率^2’, 8.715609635939173e-05),
(‘平均入住率 街区的纬度’, 0.02133445921833345),
(‘平均入住率 街区的经度’, 0.016241293829958238),
(‘街区的纬度^2’, 0.061886735759100135),
(‘街区的纬度 街区的经度’, 0.10810717326205625),
(‘街区的经度^2’, 0.039907735048536896)]

同样，这里每个列对应的值就是对应的系数，可以理解为影响结果的重要性大小。

我们也可以把这个化成dataframe格式：

coeff = pd.DataFrame([poly.get_feature_names(X.columns),reg.coef_.tolist()]).T

coeff

大家可以自行去试一试，这里截图太长就不放了。

2.2 与变换前的模型拟合效果进行比对

poly =  PolynomialFeatures(degree=4).fit(X,y)

X_ = poly.transform(X)

变换前：

lr = LinearRegression().fit(X,y)
lr.score(X,y)

0.6062326851998051

变换后的：

lr1 = LinearRegression().fit(X_,y)
lr1.score(X_,y)

0.745313897131279

通过结果不难发现，变换后的结果确实要提升不少，不过切忌degree调太高，电脑会卡死的哈哈。

另外，我这里没有划分训练集和测试集，大家也可以自己去试一试。

结束语

那么关于线性回归的介绍就到这里啦，下一篇讲啥好呢。。。

emmm，明天再看吧。

推荐关注的专栏

👨‍👩‍👦‍👦 机器学习：分享机器学习实战项目和常用模型讲解
👨‍👩‍👦‍👦 数据分析：分享数据分析实战项目和常用技能整理

机器学习系列往期回顾

💜 如何搞懂机器学习中的线性回归模型？机器学习系列之线性回归基础篇
🖤 你真的了解分类模型评估指标都有哪些吗？【附Python代码实现】
💙 一文带你用Python玩转决策树 ❤️画出决策树&各种参数详细说明❤️决策树的优缺点又有哪些？
🧡 开始学习机器学习时你必须要了解的模型有哪些？机器学习系列之决策树进阶篇
💚 开始学习机器学习时你必须要了解的模型有哪些？机器学习系列之决策树基础篇
❤️ 以❤️简单易懂❤️的语言带你搞懂有监督学习算法【附Python代码详解】机器学习系列之KNN篇
💜 开始学习机器学习之前你必须要了解的知识有哪些？机器学习系列入门篇

往期内容回顾

🖤 我和关注我的前1000个粉丝“合影”啦！收集前1000个粉丝进行了一系列数据分析，收获满满
💚 MySQL必须掌握的技能有哪些？超细长文带你掌握MySQL【建议收藏】
💜 Hive必须了解的技能有哪些？万字博客带你掌握Hive❤️【建议收藏】

CSDN@报告，今天也有好好学习