如题,以斐波那契数列为例,写以下三种递归算法进行测试:
>>> def F1(n):
if n<3: return 1
return F1(n-1)+F1(n-2)
>>> def F2(n,n2=1,n1=1):
if n<3: return 1
if n==3: return n2+n1
return F2(n-1,n1+n2,n2)
>>> def F3(n:int)->int:
if n<3: return 1
t=n//2
if n%2: return F3(t)**2+F3(t+1)**2
return F3(t)*(F3(t+1)+F3(t-1))
>>> for i in range(1,16):i,F1(i),F2(i),F3(i),F1(i)==F2(i)==F3(i)
(1, 1, 1, 1, True)
(2, 1, 1, 1, True)
(3, 2, 2, 2, True)
(4, 3, 3, 3, True)
(5, 5, 5, 5, True)
(6, 8, 8, 8, True)
(7, 13, 13, 13, True)
(8, 21, 21, 21, True)
(9, 34, 34, 34, True)
(10, 55, 55, 55, True)
(11, 89, 89, 89, True)
(12, 144, 144, 144, True)
(13, 233, 233, 233, True)
(14, 377, 377, 377, True)
(15, 610, 610, 610, True)
>>> F1 函数测试:
增加一个全局变量count用于计算调用次数。
>>> def F1(n):
global count
count += 1
if n<3: return 1
return F1(n-1)+F1(n-2)
>>> for i in range(1,16):
count=0; F1(i),count
(1, 1)
(1, 1)
(2, 3)
(3, 5)
(5, 9)
(8, 15)
(13, 25)
(21, 41)
(34, 67)
(55, 109)
(89, 177)
(144, 287)
(233, 465)
(377, 753)
(610, 1219)
>>>
>>> count=0; F1(20),count
(6765, 13529)
>>> count=0; F1(25),count
(75025, 150049)
>>> count=0; F1(30),count
(832040, 1664079)
>>> 6765*2,75025*2,832040*2
(13530, 150050, 1664080)
>>> 6765*2-1,75025*2-1,832040*2-1
(13529, 150049, 1664079)
>>> 结果真的有点出乎意料,F(n)的运行次数是 2*F(n)-1。这么巨大的数字,怪不得此函数算 F(40) 时电脑基本上就动不了,要知道 2*F(40)-1 = 204668309,两亿次的调用计算量可想而知,不只是两亿次的整数运算。
所以这个函数的时间复杂度应在立方级O(n³)和指数级O(2ⁿ)之间吧:
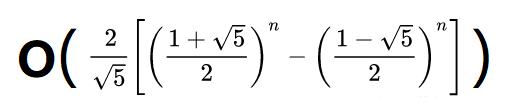
F2 函数测试:
>>> def F2(n,n2=1,n1=1):
global count
count += 1
if n<3: return 1
if n==3: return n2+n1
return F2(n-1,n1+n2,n2)
>>> for i in range(1,16):
count=0; F2(i),count
(1, 1)
(1, 1)
(2, 1)
(3, 2)
(5, 3)
(8, 4)
(13, 5)
(21, 6)
(34, 7)
(55, 8)
(89, 9)
(144, 10)
(233, 11)
(377, 12)
(610, 13)
>>>
>>> count=0; F2(100),count
(354224848179261915075, 98)
>>> count=0; F2(1000),count
(4346655768693745643568852767504062580256466051737178040248172\
90895365554179490518904038798400792551692959225930803226347752\
09689623239873322471161642996440906533187938298969649928516003\
704476137795166849228875, 998)
>>> 明显,经过尾递归优化后的时间复杂度为线性级O(n)。但是,它计算到 F(1027) 时就报错“超出了最大递归深度”,估计算法的空间复杂度已大到“内存占用”已到了堆栈限制上限了。
F3 函数测试:
>>> def F3(n:int)->int:
global count
count += 1
if n<2: return n
if n==2: return 1
t=n//2
if n%2: return F3(t)**2+F3(t+1)**2
return F3(t)*(F3(t+1)+F3(t-1))
>>> count=0; F3(100),count
(354224848179261915075, 462)
>>> count=0; F3(101),count
(573147844013817084101, 344)
>>> count=0; F3(200),count
(280571172992510140037611932413038677189525, 1131)
>>> count=0; F3(201),count
(453973694165307953197296969697410619233826, 807)
>>> 这个函数的时间复杂应该接近线性对数级 O(nlogn) 的,并且当n是奇数时比偶数时计算的快。
函数的时间测试
>>> def Fib(n):
if n<3: return 1
if n%2: return Fib(n//2)**2+Fib(n//2+1)**2
return Fib(n//2)*(Fib(n//2+1)+Fib(n//2-1))
>>> from time import time
>>> t=time();n=Fib(2000000);print(time()-t)
111.7971076965332斐波那切数列递归函数的终极改进
综合以上几个函数的经验作以下改进,改进后计算第500万项只需80秒,比不作改进的计算200万项还要快半分钟。
>>> def Fib(n:int,n1=34,n2=55):
if n<11: return [0,1,1,2,3,5,8,13,21,34,55][n]
if n==11: return n1+n2
if n<1001:return Fib(n-1,n2,n1+n2)
t=n//2
if n%2: return Fib(t)**2+Fib(t+1)**2
return Fib(t)*(Fib(t+1)+Fib(t-1))
>>> from time import time
>>> t=time();n=Fib(1000000);print(time()-t)
7.492823362350464
>>> t=time();n=Fib(2000000);print(time()-t)
18.6656014919281
>>> t=time();n=Fib(3000000);print(time()-t)
35.3787145614624
>>> t=time();n=Fib(4000000);print(time()-t)
46.64482545852661
>>> t=time();n=Fib(5000000);print(time()-t)
80.72290563583374
>>> --All done!