python深度学习入门-与学习相关的技巧_诗雨时的博客

深度学习入门-与学习相关的技巧

摘要

1. 参数的更新

1.1 SGD

1.2 SGD 的缺点

1.3 Momentum（动量）

1.4 AdaGrad

1.5 Adam

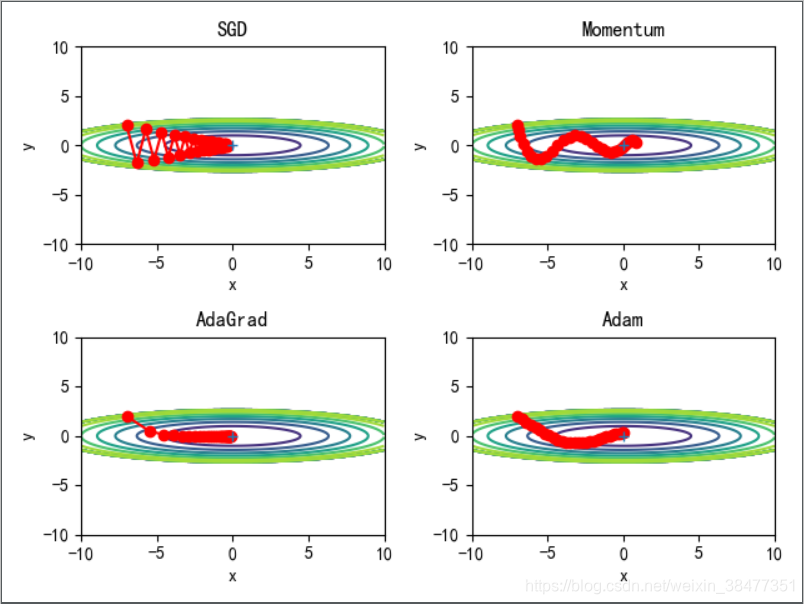
1.6 最优化方法的比较

1.7 基于 MNIST 数据集的更新方法的比较

2. 权重的初始值

3. Batch Normalization（批归一化）

4. 正则化

5. 超参数的验证

摘要

参数更新方法：SGD、Momentum、AdaGrad、Adam 等。
权重初始值的赋值方法对进行正确的学习非常重要。
作为权重初始值，Xavier 初始值、He 初始值等比较有效。
通过使用 Batch Normalization（批归一化），可以加速学习，并且对初始值变得健壮。
抑制过拟合的正则化技术有：权值衰减、Dropot 等。
逐渐缩小 “好值” 存在的范围是搜索超参数的一个有效方法。

1. 参数的更新

最优化（optimization）：

神经网络的学习的目的是找到使损失函数的值尽可能小的参数。这是寻找最优参数的问题，解决这个问题的过程称为最优化（optimization）。

随机梯度下降法（stochastic gradient descent）：

使用参数的梯度，沿梯度方向更新参数，并重复这个步骤多次，从而逐渐靠近最优参数，这个过程称为随机梯度下降法（stochastic gradient descent），简称 SGD。

1.1 SGD

SGD 用数学式表示如下式 (5.1)。

$W\leftarrow W\leftarrow \eta \frac{\partial L}{\partial W} \ \ \ \ \ \ \ \ (5.1)$

   $W$ ：需要更新的权重参数；

   $\frac{\partial L}{\partial W}$ ：损失函数关于 $W$ 的梯度；

   $\eta$ ：学习率（实际上会取 0.01 或 0.001 这些事先决定好的值）；

   $\leftarrow$ ：表示用右边的值更新左边的值。

Python 实现 SGD：

class SGD(object):
    """随机梯度下降法（Stochastic Gradient Descent）"""
    def __init__(self, lr=0.01):
        self.lr = lr    # 学习率

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]

1.2 SGD 的缺点

如果函数的形状非均向（anisotropic），比如呈延伸状，所有的路径就会非常低效。SGD 低效的根本原因是，梯度的方向并没有指向最小值的方向。

1.3 Momentum（动量）

Momentum 用数学式表示如下式 (5.2)、(5.3)。

$v\leftarrow \alpha v\leftarrow \eta \frac{\partial L}{\partial W} \ \ \ \ \ \ \ \ (5.2)$

$W\leftarrow W+v \ \ \ \ \ \ \ \ (5.3)$

   $W$ ：需要更新的权重参数；

   $\frac{\partial L}{\partial W}$ ：损失函数关于 $W$ 的梯度；

   $\eta$ ：学习率（实际上会取 0.01 或 0.001 这些事先决定好的值）；

   $v$ ：表示了物体在梯度方向上受力，在这个力的作用下，物体的速度增加这一物理法则；

   $\alpha v$ ：在物体不受任何力时，该项承担使物体逐渐减速的任务（ $\alpha$ 设定为 0.9 之类的值），对应物理上的地面摩擦力或空气阻力；

   $\leftarrow$ ：表示用右边的值更新左边的值。

Python 实现 Momentum：

import numpy as np


class Momentum(object):
    """Momentum SGD"""
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr*grads[key]
            params[key] += self.v[key]

1.4 AdaGrad

学习率衰减（learning rate decay）：

随着学习的进行，使学习率逐渐减小。

AdaGrad 用数学式表示如下式 (5.4)、(5.5)。

$h\leftarrow h + \frac{\partial L}{\partial W} * \frac{\partial L}{\partial W} \ \ \ \ \ \ \ \ (5.4)$

$W\leftarrow W - \eta \frac{1}{\sqrt{h}}\frac{\partial L}{\partial W} \ \ \ \ \ \ \ \ (5.5)$

$W$ ：需要更新的权重参数；

   $\frac{\partial L}{\partial W}$ ：损失函数关于 $W$ 的梯度；

   $\eta$ ：学习率（实际上会取 0.01 或 0.001 这些事先决定好的值）；

   $h$ ：保存了以前的所有梯度值的平方和；

   $\leftarrow$ ：表示用右边的值更新左边的值。

使用 RMSProp 方法改善 AdaGrad 无止境学习时更新量变为 0 的情况：

AdaGrad 会记录过去所有梯度的平方和。因此，学习越深入，更新的幅度就越小。实际上，如果无止境地学习，更新量就会变为 0，完全不再更新。

RMSProp 方法并不是将过去所有的梯度一视同仁地相加，而是逐渐地遗忘过去的梯度，在做加法运算时将新梯度的信息更多地反映出来。这种操作从专业上讲，称为 “指数移动平均”，呈指数函数式地减小过去的梯度的尺度。

Python 实现 AdaGrad 和 RMSProp ：

import numpy as np


class AdaGrad(object):
    """AdaGrad"""
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None
    
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
        
        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


class RMSProp(object):
    """RMSProp"""
    def __init__(self, lr=0.01, decay_rate=0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None
    
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
                
        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

1.5 Adam

Adam：直观理解，就是融合了 Momentum 和 AdaGrad 的方法。可以实现参数空间的高效搜索和进行超参数的 “偏置矫正”。论文地址：http://arxiv.org/abs/1412.6980v8。

Python 实现 Adam：

import numpy as np


class Adam(object):
    """Adam (http://arxiv.org/abs/1412.6980v8)"""
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr    # 学习率
        self.beta1 = beta1    # 一次momentum系数
        self.beta2 = beta2    # 二次momentum系数
        self.iter = 0
        self.m = None
        self.v = None

    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)

        self.iter += 1
        lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)

        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
            
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)

1.6 最优化方法的比较

import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict


"""优化器"""


class SGD(object):
    """随机梯度下降法（Stochastic Gradient Descent）"""
    def __init__(self, lr=0.01):
        self.lr = lr    # 学习率

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]


class Momentum(object):
    """Momentum SGD"""
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr*grads[key]
            params[key] += self.v[key]


class Nesterov:

    """Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.v[key] *= self.momentum
            self.v[key] -= self.lr * grads[key]
            params[key] += self.momentum * self.momentum * self.v[key]
            params[key] -= (1 + self.momentum) * self.lr * grads[key]


class AdaGrad:

    """AdaGrad"""
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


class RMSProp(object):
    """RMSProp"""
    def __init__(self, lr=0.01, decay_rate=0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


class Adam(object):
    """Adam (http://arxiv.org/abs/1412.6980v8)"""
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr    # 学习率
        self.beta1 = beta1    # 一次momentum系数
        self.beta2 = beta2    # 二次momentum系数
        self.iter = 0
        self.m = None
        self.v = None

    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)

        self.iter += 1
        lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)

        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])

            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)


"""优化器比较"""


def f(x, y):
    return x**2 / 20.0 + y**2


def df(x, y):
    return x / 10.0, 2.0 * y


init_pos = (-7.0, 2.0)
params = {}
params["x"], params["y"] = init_pos[0], init_pos[1]
grads = {}
grads["x"], grads["y"] = 0, 0

optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)

idx = 1

for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]
    
    for i in range(30):
        x_history.append(params["x"])
        y_history.append(params["y"])

        grads["x"], grads["y"] = df(params["x"], params["y"])
        optimizer.update(params, grads)

    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)

    X, Y = np.meshgrid(x, y)
    Z = f(X, Y)

    # for simple contour line
    mask = Z > 7
    Z[mask] = 0

    # plot
    plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, "o-", color="red")
    plt.contour(X, Y, Z)
    plt.ylim(-10, 10)
    plt.xlim(-10, 10)
    plt.plot(0, 0, "+")
    # colorbar()
    # spring()
    plt.title(key)
    plt.xlabel("x")
    plt.ylabel("y")

plt.show()

图 5-1 最优化方法的比较：SGD、Momentum、AdaGram、Adam

1.7 基于 MNIST 数据集的更新方法的比较

实验：

以一个 5 层神经网络为对象，其中每层有 100 个神经元。激活函数使用 ReLU。

Python 实现：

"""基于MNIST数据集的更新方法的比较"""

import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict

from dataset.mnist import load_mnist


def smooth_curve(x):
    """用于使损失函数的图形变圆滑

    参考：http://glowingpython.blogspot.jp/2012/02/convolution-with-numpy.html
    """
    window_len = 11
    s = np.r_[x[window_len-1:0:-1], x, x[-1:-window_len:-1]]
    w = np.kaiser(window_len, 2)
    y = np.convolve(w/w.sum(), s, mode='valid')
    return y[5:len(y)-5]


def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T

    x = x - np.max(x)  # 溢出对策
    return np.exp(x) / np.sum(np.exp(x))


def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)

    # 监督数据是one-hot-vector的情况下，转换为正确解标签的索引
    if t.size == y.size:
        t = t.argmax(axis=1)

    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size


def numerical_gradient(f, x):
    h = 1e-4  # 0.0001
    grad = np.zeros_like(x)

    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        idx = it.multi_index
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x)  # f(x+h)

        x[idx] = tmp_val - h
        fxh2 = f(x)  # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2 * h)

        x[idx] = tmp_val  # 还原值
        it.iternext()

    return grad


class SoftmaxWithLoss(object):

    def __init__(self):
        self.loss = None    # 损失
        self.y = None    # softmax 的输出
        self.t = None    # 监督数据(one-hot vector)

    def forward(self, x, t):
        """
        正向传播
        :param x: 输入
        :param t: 监督数据
        :return:
        """
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)

        return self.loss

    def backward(self, dout=1):
        """
        反向传播
        :param dout: 上游传来的导数
        :return:
        """
        batch_size = self.t.shape[0]
        if self.t.size == self.y.size:  # 监督数据是one-hot-vector的情况
            dx = (self.y - self.t) / batch_size
        else:
            dx = self.y.copy()
            dx[np.arange(batch_size), self.t] -= 1
            dx = dx / batch_size

        return dx


class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = sigmoid(x)
        self.out = out
        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out

        return dx


class Affine:
    def __init__(self, W, b):
        self.W = W    # 权重参数
        self.b = b    # 偏置参数

        self.x = None    # 输入
        self.original_x_shape = None    # 输入张量的形状
        self.dW = None    # 权重参数的导数
        self.db = None    # 偏置参数的导数

    def forward(self, x):
        """
        正向传播
        :param x:
        :return:
        """
        # 对应张量
        self.original_x_shape = x.shape
        x = x.reshape(x.shape[0], -1)
        self.x = x

        out = np.dot(self.x, self.W) + self.b

        return out

    def backward(self, dout):
        """
        反向传播
        :param dout: 上游传来的导数
        :return: 输入的导数
        """
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)

        dx = dx.reshape(*self.original_x_shape)  # 还原输入数据的形状（对应张量）
        return dx


class Relu(object):
    def __init__(self):
        # 由True/False构成的NumPy数组
        # 正向传播时的输入x的元素中小于等于0的地方保存为True，其他地方(大于0的元素)保存为False
        self.mask = None

    def forward(self, x):
        """
        正向传播
        :param x: 正向传播时的输入
        :return:
        """
        # 输入x的元素中小于等于0的地方保存为True，其他地方(大于0的元素)保存为False
        self.mask = (x <= 0)
        # 输入x的元素中小于等于0的值变换为0
        out = x.copy()
        out[self.mask] = 0

        return out

    def backward(self, dout):
        """
        反向传播
        :param dout: 上游传来的导数
        :return:
        """
        # 将从上游传来的dout的mask中的元素为True的地方设为0
        dout[self.mask] = 0
        dx = dout

        return dx


class MultiLayerNet:
    """全连接的多层神经网络

    Parameters
    ----------
    input_size : 输入大小（MNIST的情况下为784）
    hidden_size_list : 隐藏层的神经元数量的列表（e.g. [100, 100, 100]）
    output_size : 输出大小（MNIST的情况下为10）
    activation : 'relu' or 'sigmoid'
    weight_init_std : 指定权重的标准差（e.g. 0.01）
        指定'relu'或'he'的情况下设定“He的初始值”
        指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值”
    weight_decay_lambda : Weight Decay（L2范数）的强度
    """
    def __init__(self, input_size, hidden_size_list, output_size,
                 activation='relu', weight_init_std='relu', weight_decay_lambda=0):
        self.input_size = input_size
        self.output_size = output_size
        self.hidden_size_list = hidden_size_list
        self.hidden_layer_num = len(hidden_size_list)
        self.weight_decay_lambda = weight_decay_lambda
        self.params = {}

        # 初始化权重
        self.__init_weight(weight_init_std)

        # 生成层
        activation_layer = {'sigmoid': Sigmoid, 'relu': Relu}
        self.layers = OrderedDict()
        for idx in range(1, self.hidden_layer_num+1):
            self.layers['Affine和Softmax层的实现' + str(idx)] = Affine(self.params['W' + str(idx)],
                                                      self.params['b' + str(idx)])
            self.layers['Activation_function' + str(idx)] = activation_layer[activation]()

        idx = self.hidden_layer_num + 1
        self.layers['Affine和Softmax层的实现' + str(idx)] = Affine(self.params['W' + str(idx)],
            self.params['b' + str(idx)])

        self.last_layer = SoftmaxWithLoss()

    def __init_weight(self, weight_init_std):
        """设定权重的初始值

        Parameters
        ----------
        weight_init_std : 指定权重的标准差（e.g. 0.01）
            指定'relu'或'he'的情况下设定“He的初始值”
            指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值”
        """
        all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
        for idx in range(1, len(all_size_list)):
            scale = weight_init_std
            if str(weight_init_std).lower() in ('relu', 'he'):
                scale = np.sqrt(2.0 / all_size_list[idx - 1])  # 使用ReLU的情况下推荐的初始值
            elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
                scale = np.sqrt(1.0 / all_size_list[idx - 1])  # 使用sigmoid的情况下推荐的初始值

            self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx])
            self.params['b' + str(idx)] = np.zeros(all_size_list[idx])

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)

        return x

    def loss(self, x, t):
        """求损失函数

        Parameters
        ----------
        x : 输入数据
        t : 教师标签

        Returns
        -------
        损失函数的值
        """
        y = self.predict(x)

        weight_decay = 0
        for idx in range(1, self.hidden_layer_num + 2):
            W = self.params['W' + str(idx)]
            weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)

        return self.last_layer.forward(y, t) + weight_decay

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1 : t = np.argmax(t, axis=1)

        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

    def numerical_gradient(self, x, t):
        """求梯度（数值微分）

        Parameters
        ----------
        x : 输入数据
        t : 教师标签

        Returns
        -------
        具有各层的梯度的字典变量
            grads['W1']、grads['W2']、...是各层的权重
            grads['b1']、grads['b2']、...是各层的偏置
        """
        loss_W = lambda W: self.loss(x, t)

        grads = {}
        for idx in range(1, self.hidden_layer_num+2):
            grads['W' + str(idx)] = numerical_gradient(loss_W, self.params['W' + str(idx)])
            grads['b' + str(idx)] = numerical_gradient(loss_W, self.params['b' + str(idx)])

        return grads

    def gradient(self, x, t):
        """求梯度（误差反向传播法）

        Parameters
        ----------
        x : 输入数据
        t : 教师标签

        Returns
        -------
        具有各层的梯度的字典变量
            grads['W1']、grads['W2']、...是各层的权重
            grads['b1']、grads['b2']、...是各层的偏置
        """
        # forward
        self.loss(x, t)

        # backward
        dout = 1
        dout = self.last_layer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 设定
        grads = {}
        for idx in range(1, self.hidden_layer_num+2):
            grads['W' + str(idx)] = self.layers['Affine和Softmax层的实现' + str(idx)].dW + self.weight_decay_lambda * self.layers['Affine和Softmax层的实现' + str(idx)].W
            grads['b' + str(idx)] = self.layers['Affine和Softmax层的实现' + str(idx)].db

        return grads


class SGD(object):
    """随机梯度下降法（Stochastic Gradient Descent）"""

    def __init__(self, lr=0.01):
        self.lr = lr  # 学习率

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]


class Momentum(object):
    """Momentum SGD"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            params[key] += self.v[key]


class Nesterov:
    """Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] *= self.momentum
            self.v[key] -= self.lr * grads[key]
            params[key] += self.momentum * self.momentum * self.v[key]
            params[key] -= (1 + self.momentum) * self.lr * grads[key]


class AdaGrad:
    """AdaGrad"""

    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


class RMSProp(object):
    """RMSProp"""

    def __init__(self, lr=0.01, decay_rate=0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


class Adam(object):
    """Adam (http://arxiv.org/abs/1412.6980v8)"""

    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr  # 学习率
        self.beta1 = beta1  # 一次momentum系数
        self.beta2 = beta2  # 二次momentum系数
        self.iter = 0
        self.m = None
        self.v = None

    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)

        self.iter += 1
        lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)

        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])

            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)


"""优化器比较"""


# 0: 读入数据
(x_train, y_train), (x_test, y_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000

# 1: 进行实验的设置
optimizers = {}
optimizers["SGD"] = SGD()
optimizers["Momentum"] = Momentum()
optimizers["AdaGrad"] = AdaGrad()
optimizers["Adam"] = Adam()

networks = {}
train_loss = {}
for key in optimizers.keys():
    networks[key] = MultiLayerNet(input_size=784,
                                  hidden_size_list=[100, 100, 100, 100],
                                  output_size=10)
    train_loss[key] = []

# 2: 开始训练
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    y_batch = y_train[batch_mask]

    for key in optimizers.keys():
        grads = networks[key].gradient(x_batch, y_batch)
        optimizers[key].update(networks[key].params, grads)

        loss = networks[key].loss(x_batch, y_batch)
        train_loss[key].append(loss)

    if i % 100 == 0:
        print(f"============itrration: {i}============")
        for key in optimizers.keys():
            loss = networks[key].loss(x_batch, y_batch)
            print(f"{key}: {loss}")

# 3: 绘制图形
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()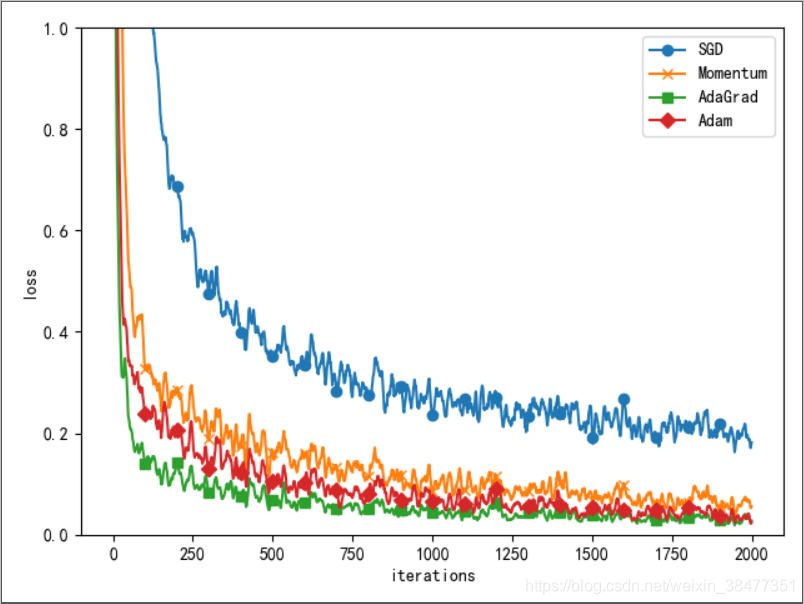

2. 权重的初始值

在神经网络的学习中，设定什么样的权重初始值，经常关系到神经网络的学习能否成功。

2.1 可以将权重初始值设为 0 吗

权值衰减（weight decay）：一种以减小权重参数的值为目的进行学习的方法。通过减小权重参数的值来抑制过拟合的发生。

为什么不能将权重初始值设为 0 呢？为什么不能将权重初始值设成一样的值呢？

因为在误差反向传播中，所有的权重值都会进行相同的更新。比如，在 2 层神经网络中，假设第 1 层和第 2 层的权重为0。这样一来，正向传播时，因为输入层的权重为 0，所以第 2 层的神经元全部会被传递相同的值。第 2 层的神经元中全部输入相同的值，这意味着反向传播时第 2 层的权重全部都会进行相同的更新。因此，权重被更新为相同的值，并拥有了对称的值（重复的值）。这使得神经网络拥有许多不同的权重的意义丧失了。

2.2 隐藏层的激活值的分布

实验：

向一个 5 层神经网络（激活函数使用 sigmoid 函数）传入随机生成的输入数据，用直方图绘制各层激活值（激活函数的输出数据）的数据分布。

实验 1：使用标准差为 1 的高斯分布作为权重初始值

各层的激活值呈偏向 0 和 1 的分布。这里使用的 sigmoid 函数是 S 型函数，随着输出不断地靠近 0（或者靠近 1），它的导数的值逐渐接近 0。

梯度消失（gradient vanishing）：偏向 0 和 1 的数据分布会造成反向传播中梯度的值不断变小，最后消失。这个问题称为梯度消失（gradient vanishing）。

实验 2：使用标准差为 0.01 的高斯分布作为权重初始值

图 5-4 使用标准差为 0.01 的高斯分布作为权重初始值时的各层激活值的分布

各层的激活值呈集中在 0.5 附近的分布。因为不像标准差为 1 时的那样偏向 0 和 1，所以不会发生梯度消失的问题。

激活值的分布有所偏向，说明表现力上会有很大问题。为什么这么说呢？因为如果有多个神经元都输出几乎相同的值，那它们就没有存在的意义了。比如，如果 100 个神经元都输出几乎相同的值，那么也可以由 1 个神经元来表达基本相同的事情。因此，激活值在分布上有所偏向会出现 “表现力受限 ” 的问题。

各层的激活值的分布都要求有适当的广度。为什么呢？

因为通过在各层间传递多样性的数据，神经网络可以进行高效的学习。反过来，如果传递的是有所偏向的数据，就会出现梯度消失或者 “表现力受限” 的问题，导致学习可能无法顺利进行。

实验 3：使用 Xavier 初始值作为权重初始值

Xavier Glorot 等人的论文中推荐的初始值：如果前一层的节点数为 n，则初始值使用标准差为 $\frac{1}{\sqrt{n}}$ 的高斯分布。

Xavier 初始值是以激活函数是线性函数为前提推导出来的。因为 sigmoid 函数和 tanh 函数左右对称，且中央附近可以视作线性函数，所以适合使用 Xavier 初始值。

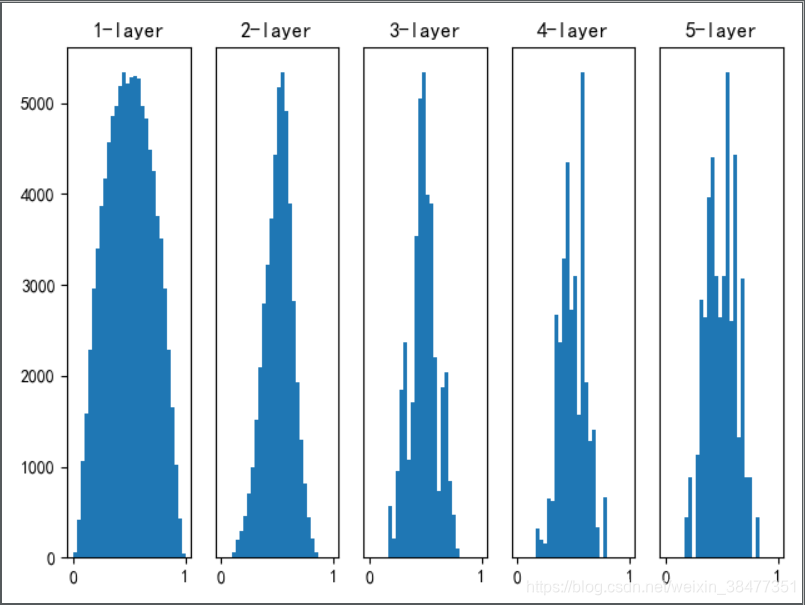
使用 Xavier 初始值后，前一层的节点数越多，要设定为目标节点的初始值的权重尺度就越小。

观察图 5-5 可知，越是后面的层，图像变得越歪斜，但是呈现了比之前更有广度的分布。因为各层间传递的数据有了适当的广度，所以 sigmoid 函数的表现力不受限制，有望进行高效地学习。

实验 4：使用 Xavier 初始值作为权重初始值时使用 tanh 函数代替 sigmoid 函数

tanh 和 sigmoid 函数都是 S型曲线函数。

tanh 函数是关于原点 (0, 0) 对称的 S 型曲线，而 sigmoid 函数是关于 (x, y) = (0, 0.5) 对称的 S 型曲线。

用作激活函数的函数最好具有关于原点对称的性质。

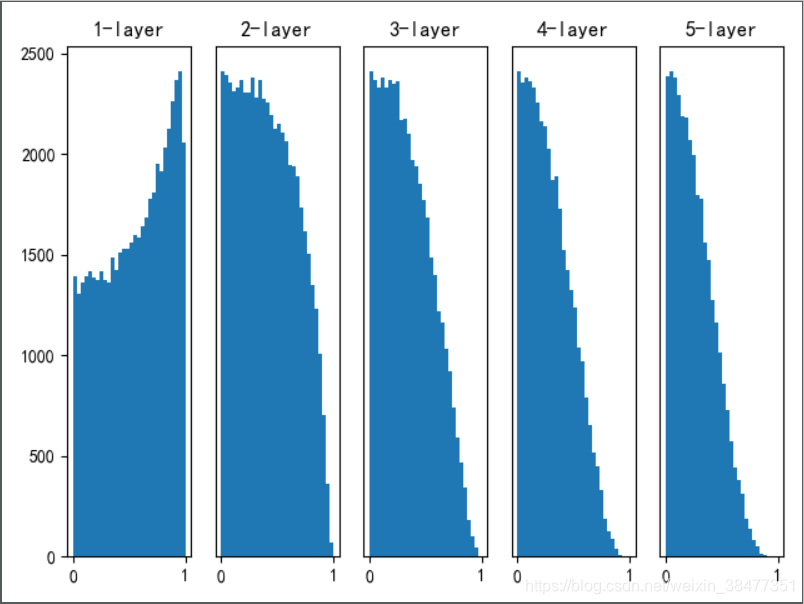
图 5-6 使用 Xavier 初始值作为权重初始值时时使用 tanh 函数代替 sigmoid 函数的各层激活值的分布

用 tanh 函数（双曲线函数）代替 sigmoid 函数，可以改善 sigmoid 函数作为激活函数时神经网络层的激活值分布呈现出稍微歪斜的形状的问题。

2.3 ReLU 的权重初始值

当激活函数使用 ReLU 函数时，一般推荐使用 ReLU 专用的初始值，也就是 Kaiming He 等人推荐的初始值，也称为 “He 初始值”。

He 初始值：当前一层的节点数为 n 时，He 初始值使用标准差为 $\sqrt{\frac{2}{n}}$ 的高斯分布。

当 Xavier 初始值是 $\sqrt{\frac{1}{n}}$ 时，（直观上）可以解释为，因为 ReLU 的负值区域的值为 0，为了使它更有广度，所以需要 2 倍的系数。

实验 1：使用标准差为 0.01 的高斯分布作为权重初始值

各层的激活值非常小（第 1 层：0.0396；第 2 层：0.00290；第 3 层：0.000197；第 4 层：1.32e-5；第 5 层：9.46e-7）。

神经网络上传递的是非常小的值，说明逆向传播时权重的梯度也同样很小。这是很严重的问题，实际上学习基本上没有进展。

实验 2：使用 Xavier 初始值作为权重初始值

随着层的加深，偏向一点点变大。

实际上，层加深后，激活值的偏向变大，学习时会出现梯度消失的问题。

实验 3：使用 ReLU 专用的 He 初始值作为权重初始值

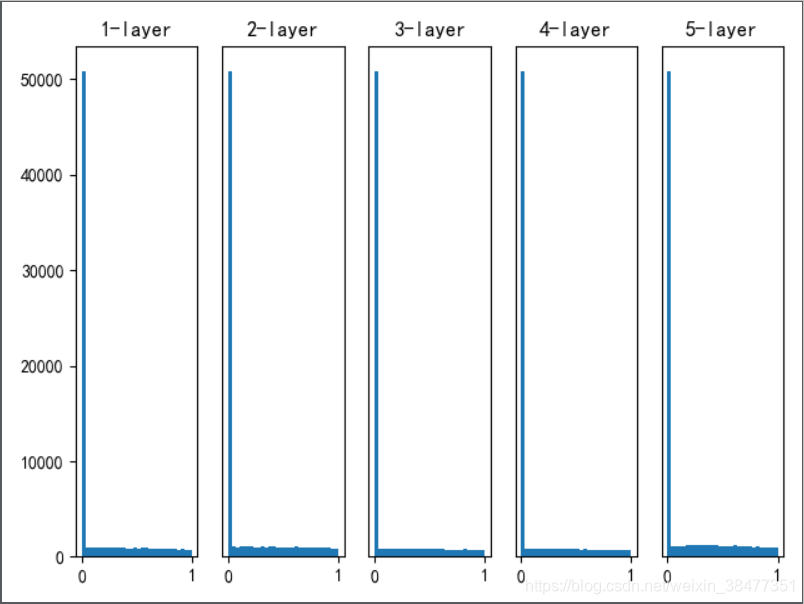
初始值为 He 初始值时，各层中分布的广度相同。

由于即便层加深，数据的广度也能保持不变，因此逆向传播时，也会传递合适的值。

总结：当激活函数使用 ReLU 函数时，权重初始值使用 He 初始值；当激活函数为 sigmoid 函数或 tanh 函数时，权重初始值使用 Xavier 初始值。

Python 代码：

"""隐藏层的激活值的分布"""

import numpy as np
from matplotlib import pyplot as plt


def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def ReLU(x):
    return np.maximum(0, x)


def tanh(x):
    return np.tanh(x)


x = np.random.randn(1000, 100)  # 1000个数据
node_num = 100  # 各隐藏层的节点（神经元）数
hidden_layer_size = 5  # 隐藏层有5层
activations = {}  # 激活值的结果保存在这里

for i in range(hidden_layer_size):
    if i != 0:
        x = activations[i - 1]

    # 改变初始值进行实验！
    # w = np.random.randn(node_num, node_num) * 1
    # w = np.random.randn(node_num, node_num) * 0.01
    # w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
    w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)

    a = np.dot(x, w)

    # 将激活函数的种类也改变，来进行实验！
    # z = sigmoid(a)
    z = ReLU(a)
    # z = tanh(a)

    activations[i] = z

# 绘制直方图
for i, a in activations.items():
    plt.subplot(1, len(activations), i+1)
    plt.title(f"{i+1}-layer")
    if i != 0: plt.yticks([], [])
    plt.hist(a.flatten(), 30, range=(0, 1))
plt.show()

2.4 基于 MNIST 数据集的权重初始值的比较

实验：

使用 MNIST 数据集，构建5 层神经网络，每层有 100 个神经元，激活函数使用 ReLU 函数。基于 std=0.01、Xavier 初始值、He 初始值进行实验，观察不同的权重初始值的赋值方法会在多大程度上影响神经网络的学习。

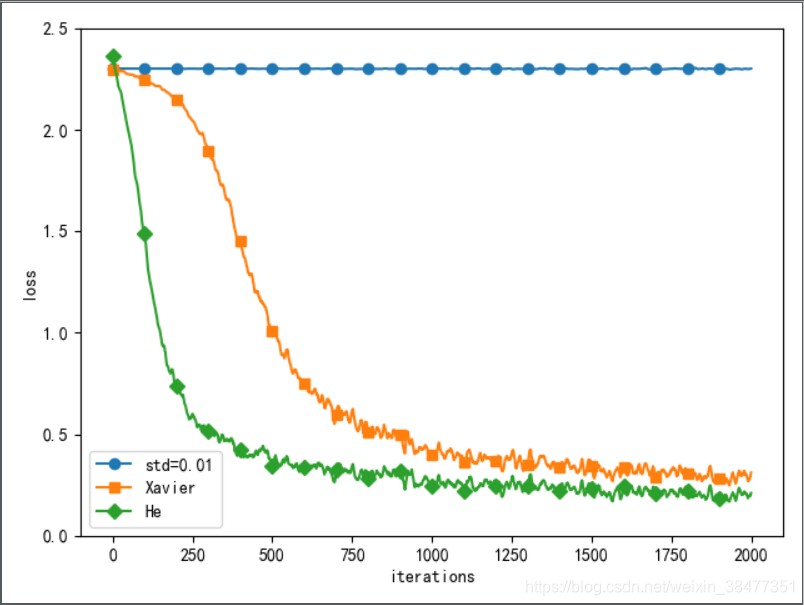
初始值为std=0.01 时，完全无法进行学习。因正向传播中传递的值很小（集中在 0 附近的数据），因此逆向传播时求到的梯度也很小，权重几乎不进行更新。

初始值为 Xavier 初始值和 He 初始值时，学习进行的很顺利。并且 He 初始值的学习进度更快一些。

Python 代码：

"""基于 MNIST 数据集的权重初始值的比较"""

import numpy as np
from collections import OrderedDict
from matplotlib import pyplot as plt

from dataset.mnist import load_mnist


def smooth_curve(x):
    """用于使损失函数的图形变圆滑

    参考：http://glowingpython.blogspot.jp/2012/02/convolution-with-numpy.html
    """
    window_len = 11
    s = np.r_[x[window_len-1:0:-1], x, x[-1:-window_len:-1]]
    w = np.kaiser(window_len, 2)
    y = np.convolve(w/w.sum(), s, mode='valid')
    return y[5:len(y)-5]


def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)

    # 监督数据是one-hot-vector的情况下，转换为正确解标签的索引
    if t.size == y.size:
        t = t.argmax(axis=1)

    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size


def numerical_gradient(f, x):
    h = 1e-4  # 0.0001
    grad = np.zeros_like(x)

    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        idx = it.multi_index
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x)  # f(x+h)

        x[idx] = tmp_val - h
        fxh2 = f(x)  # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2 * h)

        x[idx] = tmp_val  # 还原值
        it.iternext()

    return grad


def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T

    x = x - np.max(x)  # 溢出对策
    return np.exp(x) / np.sum(np.exp(x))


class SoftmaxWithLoss(object):

    def __init__(self):
        self.loss = None    # 损失
        self.y = None    # softmax 的输出
        self.t = None    # 监督数据(one-hot vector)

    def forward(self, x, t):
        """
        正向传播
        :param x: 输入
        :param t: 监督数据
        :return:
        """
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)

        return self.loss

    def backward(self, dout=1):
        """
        反向传播
        :param dout: 上游传来的导数
        :return:
        """
        batch_size = self.t.shape[0]
        if self.t.size == self.y.size:  # 监督数据是one-hot-vector的情况
            dx = (self.y - self.t) / batch_size
        else:
            dx = self.y.copy()
            dx[np.arange(batch_size), self.t] -= 1
            dx = dx / batch_size

        return dx


class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = sigmoid(x)
        self.out = out
        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out

        return dx


class Affine:
    def __init__(self, W, b):
        self.W = W    # 权重参数
        self.b = b    # 偏置参数

        self.x = None    # 输入
        self.original_x_shape = None    # 输入张量的形状
        self.dW = None    # 权重参数的导数
        self.db = None    # 偏置参数的导数

    def forward(self, x):
        """
        正向传播
        :param x:
        :return:
        """
        # 对应张量
        self.original_x_shape = x.shape
        x = x.reshape(x.shape[0], -1)
        self.x = x

        out = np.dot(self.x, self.W) + self.b

        return out

    def backward(self, dout):
        """
        反向传播
        :param dout: 上游传来的导数
        :return: 输入的导数
        """
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)

        dx = dx.reshape(*self.original_x_shape)  # 还原输入数据的形状（对应张量）
        return dx


class Relu(object):
    def __init__(self):
        # 由True/False构成的NumPy数组
        # 正向传播时的输入x的元素中小于等于0的地方保存为True，其他地方(大于0的元素)保存为False
        self.mask = None

    def forward(self, x):
        """
        正向传播
        :param x: 正向传播时的输入
        :return:
        """
        # 输入x的元素中小于等于0的地方保存为True，其他地方(大于0的元素)保存为False
        self.mask = (x <= 0)
        # 输入x的元素中小于等于0的值变换为0
        out = x.copy()
        out[self.mask] = 0

        return out

    def backward(self, dout):
        """
        反向传播
        :param dout: 上游传来的导数
        :return:
        """
        # 将从上游传来的dout的mask中的元素为True的地方设为0
        dout[self.mask] = 0
        dx = dout

        return dx


class MultiLayerNet:
    """全连接的多层神经网络

    Parameters
    ----------
    input_size : 输入大小（MNIST的情况下为784）
    hidden_size_list : 隐藏层的神经元数量的列表（e.g. [100, 100, 100]）
    output_size : 输出大小（MNIST的情况下为10）
    activation : 'relu' or 'sigmoid'
    weight_init_std : 指定权重的标准差（e.g. 0.01）
        指定'relu'或'he'的情况下设定“He的初始值”
        指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值”
    weight_decay_lambda : Weight Decay（L2范数）的强度
    """
    def __init__(self, input_size, hidden_size_list, output_size,
                 activation='relu', weight_init_std='relu', weight_decay_lambda=0):
        self.input_size = input_size
        self.output_size = output_size
        self.hidden_size_list = hidden_size_list
        self.hidden_layer_num = len(hidden_size_list)
        self.weight_decay_lambda = weight_decay_lambda
        self.params = {}

        # 初始化权重
        self.__init_weight(weight_init_std)

        # 生成层
        activation_layer = {'sigmoid': Sigmoid, 'relu': Relu}
        self.layers = OrderedDict()
        for idx in range(1, self.hidden_layer_num+1):
            self.layers['Affine和Softmax层的实现' + str(idx)] = Affine(self.params['W' + str(idx)],
                                                      self.params['b' + str(idx)])
            self.layers['Activation_function' + str(idx)] = activation_layer[activation]()

        idx = self.hidden_layer_num + 1
        self.layers['Affine和Softmax层的实现' + str(idx)] = Affine(self.params['W' + str(idx)],
            self.params['b' + str(idx)])

        self.last_layer = SoftmaxWithLoss()

    def __init_weight(self, weight_init_std):
        """设定权重的初始值

        Parameters
        ----------
        weight_init_std : 指定权重的标准差（e.g. 0.01）
            指定'relu'或'he'的情况下设定“He的初始值”
            指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值”
        """
        all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
        for idx in range(1, len(all_size_list)):
            scale = weight_init_std
            if str(weight_init_std).lower() in ('relu', 'he'):
                scale = np.sqrt(2.0 / all_size_list[idx - 1])  # 使用ReLU的情况下推荐的初始值
            elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
                scale = np.sqrt(1.0 / all_size_list[idx - 1])  # 使用sigmoid的情况下推荐的初始值

            self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx])
            self.params['b' + str(idx)] = np.zeros(all_size_list[idx])

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)

        return x

    def loss(self, x, t):
        """求损失函数

        Parameters
        ----------
        x : 输入数据
        t : 教师标签

        Returns
        -------
        损失函数的值
        """
        y = self.predict(x)

        weight_decay = 0
        for idx in range(1, self.hidden_layer_num + 2):
            W = self.params['W' + str(idx)]
            weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)

        return self.last_layer.forward(y, t) + weight_decay

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1 : t = np.argmax(t, axis=1)

        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

    def numerical_gradient(self, x, t):
        """求梯度（数值微分）

        Parameters
        ----------
        x : 输入数据
        t : 教师标签

        Returns
        -------
        具有各层的梯度的字典变量
            grads['W1']、grads['W2']、...是各层的权重
            grads['b1']、grads['b2']、...是各层的偏置
        """
        loss_W = lambda W: self.loss(x, t)

        grads = {}
        for idx in range(1, self.hidden_layer_num+2):
            grads['W' + str(idx)] = numerical_gradient(loss_W, self.params['W' + str(idx)])
            grads['b' + str(idx)] = numerical_gradient(loss_W, self.params['b' + str(idx)])

        return grads

    def gradient(self, x, t):
        """求梯度（误差反向传播法）

        Parameters
        ----------
        x : 输入数据
        t : 教师标签

        Returns
        -------
        具有各层的梯度的字典变量
            grads['W1']、grads['W2']、...是各层的权重
            grads['b1']、grads['b2']、...是各层的偏置
        """
        # forward
        self.loss(x, t)

        # backward
        dout = 1
        dout = self.last_layer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 设定
        grads = {}
        for idx in range(1, self.hidden_layer_num+2):
            grads['W' + str(idx)] = self.layers['Affine和Softmax层的实现' + str(idx)].dW + self.weight_decay_lambda * self.layers['Affine和Softmax层的实现' + str(idx)].W
            grads['b' + str(idx)] = self.layers['Affine和Softmax层的实现' + str(idx)].db

        return grads


class SGD(object):
    """随机梯度下降法（Stochastic Gradient Descent）"""

    def __init__(self, lr=0.01):
        self.lr = lr  # 学习率

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]


# 0: 读入数据
(x_train, y_train), (x_test, y_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000

# 1: 进行实验的设置
weight_init_types = {"std=0.01": 0.01, "Xavier": "sigmoid", "He": "relu"}
optimizer = SGD(lr=0.01)

networks = {}
train_loss = {}
for key, weight_type in weight_init_types.items():
    networks[key] = MultiLayerNet(input_size=784,
                                  hidden_size_list=[100, 100, 100, 100],
                                  output_size=10,
                                  weight_init_std=weight_type)
    train_loss[key] = []

# 2: 开始训练
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    y_batch = y_train[batch_mask]

    for key in weight_init_types.keys():
        grads = networks[key].gradient(x_batch, y_batch)
        optimizer.update(networks[key].params, grads)

        loss = networks[key].loss(x_batch, y_batch)
        train_loss[key].append(loss)

    if i % 100 == 0:
        print(f"============iteration: {i}========")
        for key in weight_init_types.keys():
            loss = networks[key].loss(x_batch, y_batch)
            print(f"{key}: {loss}")

# 3: 绘制图形
markers = {"std=0.01": "o", "Xavier": "s", "He": "D"}
x = np.arange(max_iterations)
for key in weight_init_types.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 2.5)
plt.legend()
plt.show()

3. Batch Normalization（批归一化）

3.1 Batch Normalization 的算法

Batch Normalization 的优点：

可以使学习快速进行（可以增大学习率）。
不那么依赖初始值（对于初始值不用那么神经质）。
抑制过拟合（降低 Dropout 等的必要性）。

Batch Normalization 的思路：调整各层的激活值分布使其拥有适当的广度。

使用 Batch Normalization 层的神经网络：

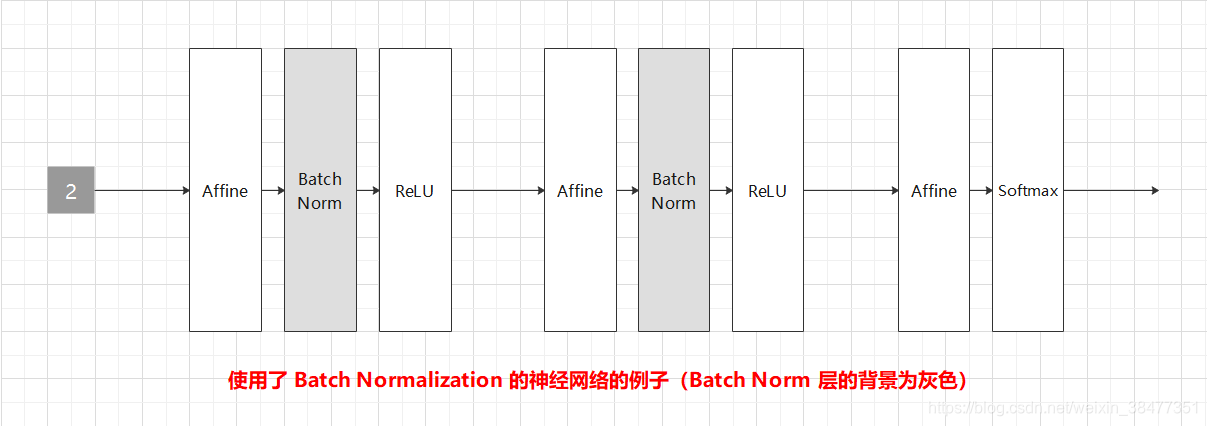
Batch Normalization，顾名思义，以进行学习时的 mini-batch 为单位，按 mini-batch 进行正规化。具体而言，就是进行使数据分布的均值为 0、方差为 1 的正规化。用数学式表示如式 (5.6)。

$\mu B \leftarrow \frac{1}{m}\sum_{i=1}^{m}x_{i}$

$\sigma ^{2}B\leftarrow \frac{1}{m}\sum_{i=1}^{m}(x_{i}-\mu B)^{2} \ \ \ \ \ \ (5.6)$

$\hat{x_{i}}\leftarrow \frac{x_{i} - \mu B}{\sqrt{\sigma ^{2}B+\varepsilon }}$

   $B$ ：mini-batch 的 $m$ 个输入数据的集合 $B=\begin{Bmatrix} x_{1}, & x_{2},& ,..., & x_{m} \end{Bmatrix}$ 。

   $\mu B$ ：均值。

   $\sigma ^{2}B$ ：方差。

式 (5.6) 所做的是将 mini-batch 的输入数据 $\begin{Bmatrix} x_{1}, & x_{2},& ,..., & x_{m} \end{Bmatrix}$ 变换为均值为 0、方差为 1 的数据 $\begin{Bmatrix} \hat{x_{1}}, & \hat{x_{2}}, & ..., & \hat{x_{m}} \end{Bmatrix}$ 。