理解神经网络的本质

一、前言

最近深度学习是一个比较热门的词，各行各业都声称自己使用了深度学习技术。现在“深度学习”这个词，就像印在球鞋上的“Fashion”、“Sport”。那深度学习到底是什么呢？

深度学习是机器学习的一个分支，当我们使用了“深度神经网络”算法进行机器学习时，我们就可以说自己在搞深度学习。而这个“神经网络”算法就是我们今天的主题。

关于机器学习的内容，各位读者可以参考Python快速构建神经网络。

在本文我依然是从线性回归开始说起。在上一篇文章，只是简单说了一下神经网络，却没有详细说神经网络的本质。在本文，作者将为大家详细说说，神经网络的全貌。

二、线性回归

2.1、直线方程

如果说线性回归很多读者没有听过的话，那么我相信你应该听过直线方程。在中学的学习中，我们通常会用下面的方程表示一根直线：
y = k x + b y = kx + b y=kx+b
其实线性回归也是这么一个简单的方程，或者说函数。我们现在回到初中，来解决下面这个问题。

直线l经过点A（1, 4），和点B（3， 7），求直线l的方程。

这个问题很简单，我们只需要将A、B点带入y = kx + b就可以得到下面方程组：
{ 4 = k + b 7 = 3 k + b \begin{cases} 4 = k + b \\ 7 = 3k + b \end{cases} {4=k+b7=3k+b​
由上面的方程组，我们可以解出：
{ k = 1.5 b = 2.5 \begin{cases} k = 1.5 \\ b = 2.5 \end{cases} {k=1.5b=2.5​

于是我们得到直线方程：
y = 1.5 x + 2.5 y = 1.5x + 2.5 y=1.5x+2.5
在我们得到直线方程后，我们对于任意给定的x，都能知道它对应的y。现在我们需要对问题进行调整。

2.2、线性回归

现在我们有下面这组数据：

(1, 12)
(2, 16)
(3, 22)
(4, 26)
(5, 29)
(6, 33)
(7, 37)
(8, 41)
(9, 45)
(10, 48)

我们还是假设上面的点都在一条直线上，这时候我们先取点(1,12)和点(4,26)，我们可以算出直线方程为如下：
y = 4 x + 8 y = 4x + 8 y=4x+8
现在我们再选取点(2,16)和点(6,33)，我们可以计算出下面的直线方程：
y = 17 4 x + 15 2 y = \frac{17}{4}x + \frac{15}{2} y=417​x+215​
由此可以看到这四个点并不在同一条直线上。但是对比斜率和截距又发现，两者很相近。所以我们可以找一条折中的直线来拟合所有的点。

我们从数据中，找到这条最优（较优）的直线的过程就叫做线性回归。

三、非线性的问题

3.1、分段函数

在前面，我们讨论的数据都是从一条直线中产生的。但是有时候我们的数据的分布可能并没有那么简单，我们的数据分布可能更接近一个分段函数，比如下面的图片：

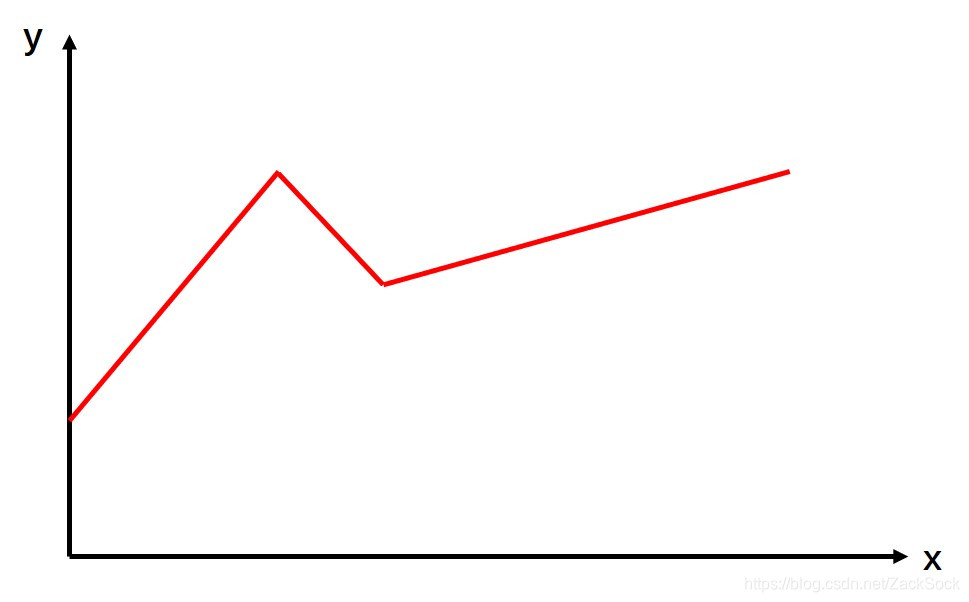
这个时候用线性方程就表示不了我们数据的分布。那我们要怎么表示上面的方程呢？

我们可以把上面的函数看出是一系列特殊函数的相加，这个特殊函数的图像如下：

从图像可以看出，这个函数只在某一个范围内有斜率。在范围左侧的值为0，当超出范围右侧后值不再改变。我们可以通过调整这个函数的斜率以及斜率生效的范围，来得到各式各样的函数，比如下面几个：

函数1到4都是都是通过调节特殊函数的斜率以及斜率生效范围生成的。只有第一个函数比较特别，它的斜率生效范围为空。

那么我们怎么用这些特殊函数组成一个分段函数呢？其实只要你仔细观察，就会发现把这四个函数相加就是我们最开始的分段函数。如下图，这里为了方便观看将特殊函数移动了位置。

现在我们可以把上面的函数简写成：
y = f 1 ( x ) + f 2 ( x ) + f 3 ( x ) + f 4 ( x ) y = f1(x) + f2(x) + f3(x) + f4(x) y=f1(x)+f2(x)+f3(x)+f4(x)
为了更直观看到效果。下面我们用程序来合成一下这个分段函数。

3.2、合成分段函数

我们先编写一个创建特殊函数的函数，代码如下：

def create_special(x, start, end, k):
    f = []
    temp = 0
    for i in x:
        # 当小于起始值函数值为0
        if i <= start:
            f.append(0)
        # 当在一定范围，为一个截距为0，斜率为k的直线
        elif start < i <= end:
            # 这里start不为0，所以我们需要减去它，保证函数截距为0，然后乘k
            f.append((i - start) * k)
            # 记录最后的值
            temp = (i - start) * k
        # 当超出范围则值保持不变
        else:
            f.append(temp)
    return np.array(f)

我们来用上面的函数绘制几个图像：

import numpy as np
import matplotlib.pyplot as plt


def create_special(x, start, end, k):
    pass


if __name__ == '__main__':
    x = np.linspace(0, 20, 200)
    y1 = create_special(x, 10, 20, 2)
    y2 = create_special(x, 5, 10, 3)
    y3 = create_special(x, 0, 15, -4)
    y4 = create_special(x, 0, 12, 1)
    plt.subplot(221)
    plt.plot(x, y1)
    plt.title("k = 2")
    plt.subplot(222)
    plt.plot(x, y2)
    plt.title("k = 3")
    plt.subplot(223)
    plt.plot(x, y3)
    plt.title("k = -4")
    plt.subplot(224)
    plt.plot(x, y4)
    plt.title("k = 1")
    plt.show()

绘制的图像如下：

可以看到，生成了我们想要的特殊函数。于是我们就可以用这些特殊函数来拟合一些分段函数，下面是其中一个例子：

import numpy as np
import matplotlib.pyplot as plt


def create_special(x, start, end, k):
    pass


if __name__ == '__main__':
    x = np.linspace(0, 20, 200)
    y1 = create_special(x, 0, 10, 2)
    y2 = create_special(x, 10, 15, -3)
    y3 = create_special(x, 15, 20, 1)
    y = 3 + y1 + y2 + y3
    plt.plot(x, y, c='r')
    plt.show()

我们生成的图像如下：

我们只要合适的特殊函数就能拟合所有的分段函数。

3.3、连续函数

在上面我们讨论的是分段函数，但是生活中有许多情况我们的数据是有一个连续函数产生的。比如我们的数据分布情况可能如下图：

这个时候我们要怎么用特殊函数表示呢？

其实这个也非常简单，我们只需要把连续的函数拆分成一个分成很多断的分段函数即可，我们可以拆分成如下图：

当我们分得足够细时，这个分段函数就可以很好的拟合连续函数。现在我们把连续函数转换成了分段函数，接下来又可以用特殊函数来组合成我们的分段函数。这样我们就可以通过特殊函数实现连续函数的拟合。

四、神经网络

4.1、激活函数

接下来我们来看一个特殊的函数，它的数学式如下：
y = c 1 1 + e − ( b + w x ) y = c\frac{1}{1 + e^{-(b + wx)}} y=c1+e−(b+wx)1​
其中c、b、w是三个参数。我们来看看c=1，b=0，w=1时的图像：

从样子上来看，和我们前面说的特殊函数很像。其实这个就是鼎鼎大名的sigmoid函数，使用特殊函数能完成的事情，sigmoid也是可以完成的。我们可以尝试使用不同的参数对比一下：

当我们调节k值时，sigmoid函数的斜率（如果近似看出特殊函数）在变换。调节b时，函数在左右移动。调节c时，函数在上下波动。

因此我们只需要调节这几个参数，就可以构造任意的特殊函数，也就能拟合任意的函数。

4.2、神经网络

我们有了sigmoid函数后，我们的一元复合函数就可以写成：
y = s i g m o i d 1 ( x ) + s i g m o i d 2 ( x ) + ⋅ ⋅ ⋅ + s i g m o i d n ( x ) y = sigmoid_1(x) + sigmoid_2(x) +···+sigmoid_n(x) y=sigmoid1​(x)+sigmoid2​(x)+⋅⋅⋅+sigmoidn​(x)
其中下标用来区分sigmoid的不同参数。我们用图示来表示上面的函数：

我们将x作为输入，然后经过数个sigmoid函数，然后相加后输入y。从图可以看出，其实我们的sigmoid函数就是常说的神经元，而一个由sigmoid函数复合而成的复合函数就是一层网络。

下面我们来看多元的情况，多元复合函数形式如下：
y = ∑ i = 1 n ∑ j = 1 n s i g m o i d i ( x j ) y = \sum_{i=1}^n\sum_{j=1}^nsigmoid_i(x_j) y=i=1∑n​j=1∑n​sigmoidi​(xj​)
多元复合函数的图示如下：

这幅图就是我们常说的全连接神经网络，不过这个神经网络只有一层。这下，我们就揭开了单层神经网络的面纱了。理论上来讲，只要我们有足够多的神经元，我们就可以拟合任何复杂的函数。但是实际情况却又很多问题。

现在我们都知道，现在优秀的网络通常都不是单层的。这部分原因，下次为大家解答。感谢阅读~