【机器学习】解开反向传播算法的奥秘

---

?个人主页: 鑫宝Code
?热门专栏: 闲话杂谈｜ 炫酷HTML | JavaScript基础
​?个人格言: "如无必要，勿增实体"

---

文章目录

解开反向传播算法的奥秘反向传播算法的概述反向传播算法的数学推导1. 前向传播2. 计算损失函数3. 计算梯度4. 更新参数 反向传播算法在深度神经网络中的应用反向传播算法的局限性和发展总结

解开反向传播算法的奥秘

在深度学习领域,反向传播算法(Back Propagation)是训练神经网络的核心算法之一。它通过计算损失函数关于网络权重的梯度,并利用梯度下降法更新权重,从而实现了神经网络的有效训练。反向传播算法的出现,解决了传统神经网络难以训练的瓶颈,推动了深度学习的蓬勃发展。本文将深入探讨反向传播算法的原理、数学推导,以及在实践中的应用,帮助读者更好地理解和掌握这一重要算法。

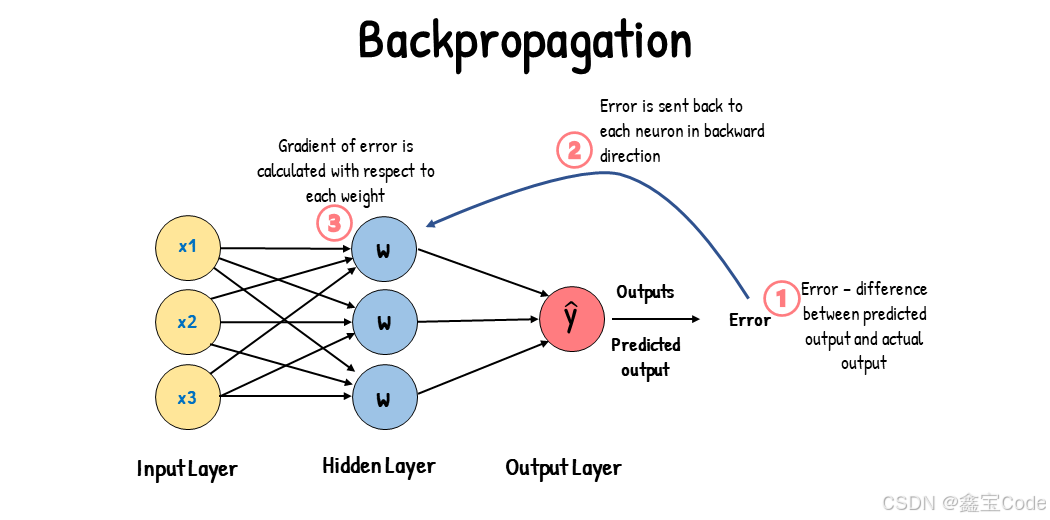
反向传播算法的概述

在训练神经网络时,我们需要不断调整网络的权重和偏置参数,使得网络在训练数据上的输出值尽可能接近期望的目标值。这个过程可以看作是一个优化问题,目标是最小化一个损失函数(Loss Function)。

反向传播算法就是用于计算损失函数关于网络参数的梯度的算法。它由两个核心步骤组成:

前向传播(Forward Propagation):输入数据经过神经网络的层层传递,计算出网络的输出值。反向传播(Back Propagation):根据网络输出值和目标值计算损失函数,并计算损失函数关于网络参数的梯度,用于更新参数。

通过不断重复这两个步骤,神经网络的参数就会不断被优化,使得网络在训练数据上的输出值逐渐接近期望的目标值。

反向传播算法的数学推导

为了更好地理解反向传播算法,让我们通过数学推导来深入探讨其原理。我们将以一个简单的单层神经网络为例,推导反向传播算法的具体计算过程。

假设我们有一个单层神经网络,输入为 x = ( x 1 , x 2 , … , x n ) \mathbf{x} = (x_1, x_2, \ldots, x_n) x=(x1​,x2​,…,xn​),权重为 W = ( w 1 , w 2 , … , w n ) \mathbf{W} = (w_1, w_2, \ldots, w_n) W=(w1​,w2​,…,wn​),偏置为 b b b,激活函数为 f f f,输出为 y y y。我们的目标是最小化损失函数 L ( y , t ) L(y, t) L(y,t),其中 t t t是期望的目标值。

1. 前向传播

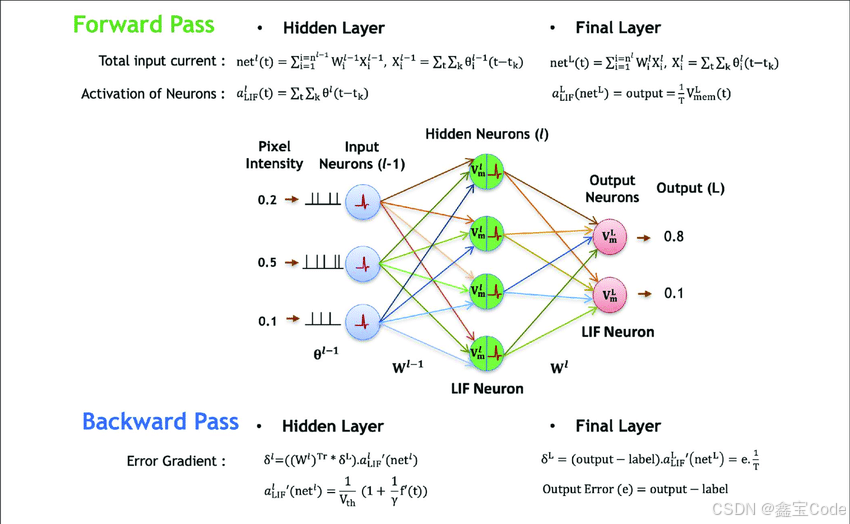
在前向传播阶段,我们计算神经网络的输出值 y y y:

y = f ( ∑ i = 1 n w i x i + b ) y = f\left(\sum_{i=1}^{n} w_i x_i + b\right) y=f(i=1∑n​wi​xi​+b)

2. 计算损失函数

接下来,我们计算损失函数 L ( y , t ) L(y, t) L(y,t)。常见的损失函数包括均方误差(Mean Squared Error, MSE)和交叉熵损失函数(Cross-Entropy Loss)等。

3. 计算梯度

为了更新网络参数,我们需要计算损失函数关于权重 W \mathbf{W} W和偏置 b b b的梯度。根据链式法则,我们有:

∂ L ∂ w i = ∂ L ∂ y ⋅ ∂ y ∂ w i \frac{\partial L}{\partial w_i} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial w_i} ∂wi​∂L​=∂y∂L​⋅∂wi​∂y​

∂ L ∂ b = ∂ L ∂ y ⋅ ∂ y ∂ b \frac{\partial L}{\partial b} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial b} ∂b∂L​=∂y∂L​⋅∂b∂y​

其中,

∂ y ∂ w i = x i f ′ ( net ) \frac{\partial y}{\partial w_i} = x_i f'(\text{net}) ∂wi​∂y​=xi​f′(net)

∂ y ∂ b = f ′ ( net ) \frac{\partial y}{\partial b} = f'(\text{net}) ∂b∂y​=f′(net)

这里, net = ∑ i = 1 n w i x i + b \text{net} = \sum_{i=1}^{n} w_i x_i + b net=∑i=1n​wi​xi​+b,表示神经元的加权输入; f ′ f' f′是激活函数的导数。

4. 更新参数

最后,我们使用梯度下降法更新网络参数:

w i ← w i − η ∂ L ∂ w i w_i \leftarrow w_i - \eta \frac{\partial L}{\partial w_i} wi​←wi​−η∂wi​∂L​

b ← b − η ∂ L ∂ b b \leftarrow b - \eta \frac{\partial L}{\partial b} b←b−η∂b∂L​

其中, η \eta η是学习率,控制了参数更新的步长。

通过不断重复前向传播和反向传播的过程,网络参数就会不断被优化,使得网络在训练数据上的输出值逐渐接近期望的目标值。

反向传播算法在深度神经网络中的应用

上述推导过程是针对单层神经网络的,对于深度神经网络,反向传播算法的计算过程会更加复杂。然而,其基本思想是相同的:计算损失函数关于每一层的参数的梯度,并利用梯度下降法更新参数。

在深度神经网络中,反向传播算法需要通过链式法则,逐层计算梯度,这个过程被称为"反向传播"。具体来说,我们从输出层开始,计算损失函数关于输出层参数的梯度;然后,沿着网络的反方向,逐层计算梯度,直到输入层。这个过程可以利用动态规划的思想,避免重复计算,从而提高计算效率。

在实践中,反向传播算法通常与一些优化技巧相结合,如momentum、RMSProp、Adam等,以加快收敛速度和提高训练效率。此外,还可以引入正则化技术,如L1/L2正则化、Dropout等,以防止过拟合。

反向传播算法的局限性和发展

尽管反向传播算法在深度学习领域取得了巨大成功,但它也存在一些局限性和挑战。

首先,反向传播算法依赖于梯度信息,因此对于存在梯度消失或梯度爆炸问题的深度神经网络,训练效果可能不佳。为了解决这个问题,研究人员提出了一些新型的优化算法,如LSTM、GRU等,以缓解梯度问题。

其次,反向传播算法的计算复杂度较高,尤其是对于大规模深度神经网络,训练过程可能需要消耗大量的计算资源。因此,提高反向传播算法的计算效率是一个重要的研究方向。

此外,反向传播算法也存在一些理论上的局限性,如无法解释神经网络的"黑箱"行为、无法处理非differentiable的函数等。为了解决这些问题,研究人员正在探索新型的机器学习范式,如强化学习、元学习等,以期突破反向传播算法的局限。

总结

反向传播算法是深度学习领域的核心算法之一,它通过计算损失函数关于网络参数的梯度,并利用梯度下降法更新参数,实现了神经网络的有效训练。本文详细介绍了反向传播算法的原理、数学推导,以及在深度神经网络中的应用。同时,也讨论了反向传播算法的局限性和发展方向。

虽然反向传播算法取得了巨大成功,但它并非万能。未来,随着机器学习技术的不断发展,必将会出现更加先进的训练算法,推动人工智能的进一步发展。让我们拭目以待,共同见证机器学习算法的新篇章!