一、为什么要引入双边带调制(DSB)?
AM信号可表示为:
![]()
其中,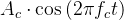 就是载波分量,它是一个不携带任何信息的纯正弦波。 如果将直流Ac去掉,即可得到一种高调制效率的调制方式——DSB调制。此时,DSB信号的全部功率都用于信息传输,调制效率是100%。
就是载波分量,它是一个不携带任何信息的纯正弦波。 如果将直流Ac去掉,即可得到一种高调制效率的调制方式——DSB调制。此时,DSB信号的全部功率都用于信息传输,调制效率是100%。
二、DSB调制与解调的原理
AM(幅度调制)和DSB(双边带调制)密切相关,从表达式上对比两种调制方式更为直观。
DSB调制的表达式为:
![]()
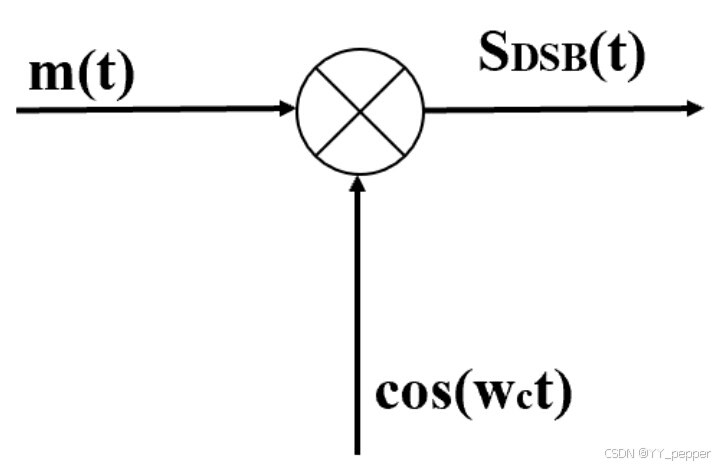
与AM调制相比,DSB调制去掉了载波部分,只保留了调制信号,这意味着节省了功率,因为载波部分在接收时并不携带信息。 DSB调制的原理图如下图所示:
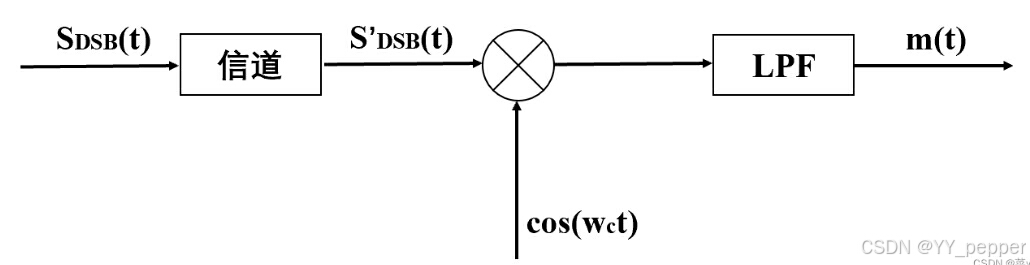
但DSB信号的包络不再与调制信号变化规律一致,解调时只能采用相干解调。DSB解调的原理图如下图所示:
三、matlab代码实现
1.DSB.m
% DSB调制解调过程close all; clc;%% 基本参数fm = 100; %基带信号频率T = 2; %基带信号时长fs = 20000; %采样频率,满足奈奎斯特采样定理dt = 1/fs; %采样间隔N = T/dt; %采样点数t = 0:dt:(N-1)*dt; %采样点的时间序列,作为横坐标%% ******************调制信号时域波形******************Am = 1;%基带信号幅值mt = Am*cos(2*pi*fm*t); %基带信号时域表达式figure(1); %创建新图像subplot(3,2,1); %创建3×2的子图集合,显示在(1,1)位置plot(t,mt,'Linewidth',1); %绘图,线宽为1xlabel('时间/t');ylabel('幅度');title('调制信号时域波形');axis([0,0.1,-1.1,1.1]); %横纵坐标范围[xmin,xmax,ymin,ymax]%% ******************调制信号频域波形******************[f,mf] = T2F(t,mt);subplot(3,2,2);plot(f,mf,'r','Linewidth',1);xlabel('f/Hz');ylabel('幅度');title('调制信号的频谱');axis([-150,150,-inf,inf]);%% ******************载波信号时域波形******************fc = 1000; %载波频率zaibo = cos(2*pi*fc*t); %载波时域表达式subplot(3,2,3);plot(t,zaibo,'Linewidth',1);xlabel('t/时间');ylabel('幅度');title('载波信号时域波形');axis([0,0.01,-1.1,1.1]);%% ******************载波信号频域波形******************[f1,zaibof] = T2F(t,zaibo);subplot(3,2,4);plot(f1,zaibof,'r','Linewidth',1);xlabel('f/Hz');ylabel('幅度');title('载波信号的频谱');axis([-1200,1200,-inf,inf]);%% ******************DSB波信号时域波形*****************dsb = mt.*zaibo;subplot(3,2,5);plot(t,dsb,'Linewidth',1);xlabel('t/时间');ylabel('幅度');title('DSB调制信号');axis([0,0.02,-1.5,1.5]);%% ******************DSB波信号频域波形*****************[f2,dsbf] = T2F(t,dsb);subplot(3,2,6);plot(f2,dsbf,'r','Linewidth',1);xlabel('f/Hz');ylabel('幅度');title('DSB波信号的频谱');axis([-1500,1500,-inf,inf]);%% ******************相干解调*****************%% ****************已调信号与载波信号相乘的时域图***************SNR = 20;awgn(dsb,SNR,'measured'); %信道传输,考虑有噪声干扰st = dsb.*zaibo;figure(2);subplot(2,1,1);plot(t,st,'Linewidth',1);xlabel('t/时间');ylabel('幅度');title('已调信号与载波信号相乘');axis([0,0.02,-1.5,1.5]);%% ****************已调信号与载波信号相乘的频谱图***************[f3,stf] = T2F(t,st);subplot(2,1,2);plot(f3,stf,'r','Linewidth',1);xlabel('f/Hz');ylabel('幅度');title('已调信号与载波相乘的频谱');axis([-150,150,-inf,inf]);%% ********************解调出来的信号******************yf = lpf(f3,stf,2*fm); %低通滤波[t,yt] = F2T(f3,yf); %做IFFT变换figure(3);subplot(2,1,1);plot(t,2*yt,'Linewidth',1);xlabel('t/时间');ylabel('幅度');title('解调出来的信号');axis([0,0.1,-1.1,1.1]);%% ***********************原信号***********************subplot(2,1,2);plot(t,mt,'g','Linewidth',1);xlabel('t/时间');ylabel('幅度');title('原信号');axis([0,0.1,-1.1,1.1]);2.T2F.m
%傅里叶变换function [f,mf] = T2F(t,mt)N = length(t); %采样点数T = t(end); %输入信号的时间最大值为Tdf = 1/T; %频谱分辨率f = -N/2*df:df:N/2*df-df; %频率分布,作频谱图的横坐标mf = fft(mt); %做FFTmf = T/N*fftshift(mf); %频谱搬移+归一化3.F2T.m
%傅里叶逆变换(IFFT)function [t,yt] = F2T(f,yf)df = f(2)-f(1);N = length(f);fmax = (f(end)-f(1)+df); %不能像T2F里T=t(end) %因为t是从0开始, %但f是经过搬移的不是从0开始dt = 1/fmax;t = 0:dt:dt*(N-1);yf = fftshift(yf); %千万别忘!将0-fs频谱搬到-fs/2-fs/2yt = fmax*ifft(yf); %不要忘记归一化*fmaxyt = real(yt); %取实部4.lpf.m
%低通滤波器function yf = lpf(f,sf,B)N = length(f); %采样点数df = f(2)-f(1); %频率间隔ym = zeros(1,N); %创建1×N的全零数组xm = floor(B/df); %带宽/频率间隔,向下取整,计算需要的采样点数xm_shift = [-xm:xm-1]+floor(N/2); % 因为前面做FFT将0频率搬移到中心处, % 因此,低通低频频率相应地搬移fN/2,才是对应的频率点ym(xm_shift) = 1; % 低通通过频率处幅度为1,其余为0,相当于理想低通yf = ym.*sf; %信号经过理想低通滤波器四、结果图
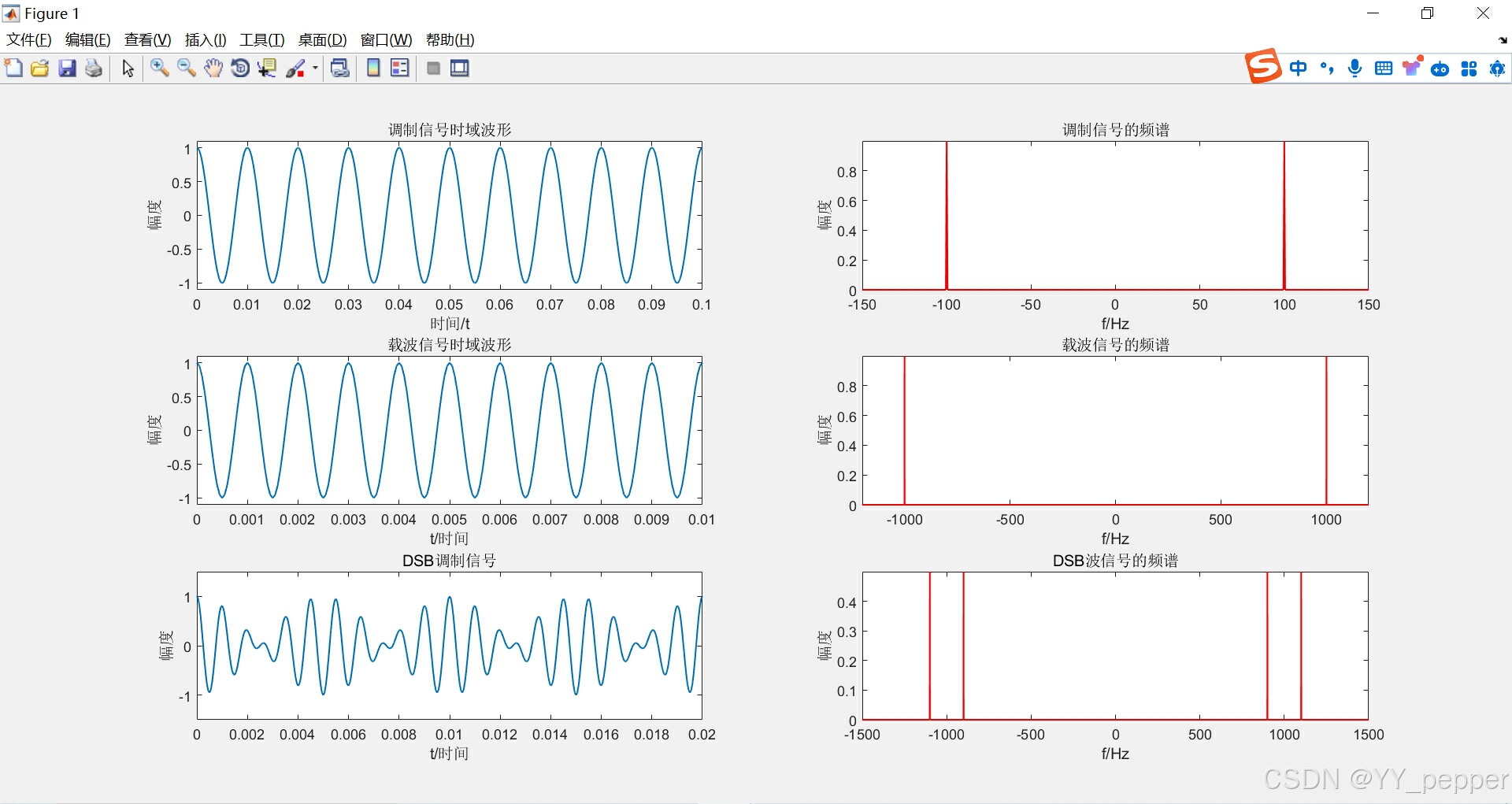
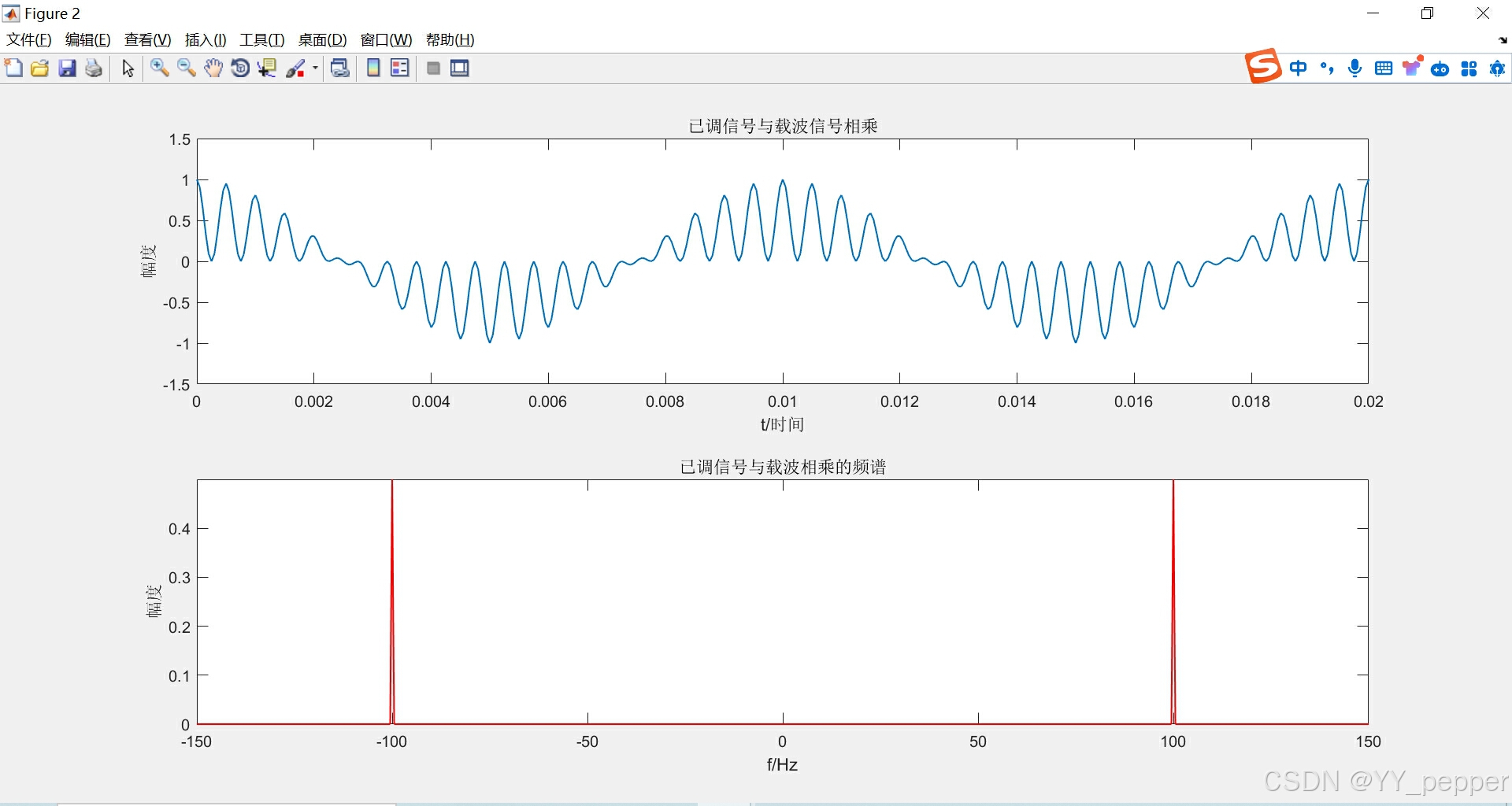
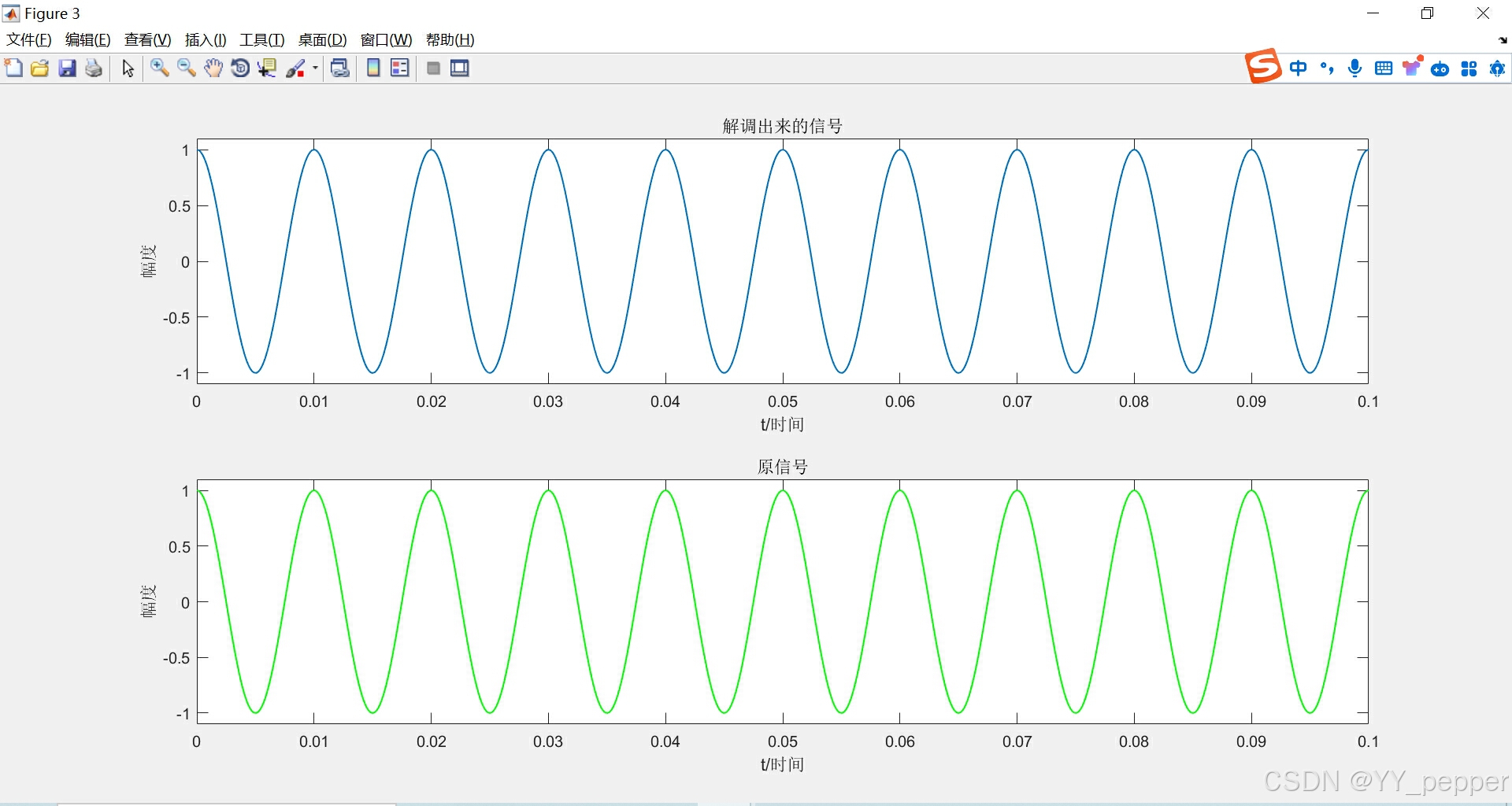
五、思考
1.注意区别F2T.m与T2F.m中fmax与T的求法
fmax = f(end)-f(1)+df ;
T = t(end) ;
t 我们设定起始点为0,因此时间长度为t 的终点。而 f 我们进行了搬移,起始点不为0,只能用差值来计算带宽。另外,还需注意末尾+df,将f(end)的值也包含进去。
2.做 ifft 时,也不要忘记 fftshift() 先进行频谱搬移
参考
DSB的调制与解调 https://blog.csdn.net/qq_47598782/article/details/128303744?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522172378777616800226565959%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=172378777616800226565959&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~top_positive~default-1-128303744-null-null.nonecase&utm_term=DSB%E8%B0%83%E5%88%B6&spm=1018.2226.3001.4450
https://blog.csdn.net/qq_47598782/article/details/128303744?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522172378777616800226565959%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=172378777616800226565959&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~top_positive~default-1-128303744-null-null.nonecase&utm_term=DSB%E8%B0%83%E5%88%B6&spm=1018.2226.3001.4450