A 题 马赛克瓷砖选色问题
选近似颜色的瓷砖,可以直接用距离公式搞定,matlab中用距离pdist2函数解决,edit pdist2后可以看到有很多种距离公式算法

很多小朋友到这里就完事了,其实不然,举个例子,三个颜色矩阵[0.6,0.6,0.6]、[0.5,0.5,0.5]、[0.5,0.6732,0.5],其中1和3和2欧式距离都相差0.1732距离,依次可视化颜色矩阵后

可以看出我们还应考虑的是 RGB 差值的方差,例如[0.6,0.6,0.6]与[0.5,0.5,0.5]做差后差 值一样,其方差为 0;[0.5,0.5,0.5]与[0.5,0.6732,0.5]做差后得到[0,1.732,0],其方差为 1;两 个公式后者作为优先排序条件,前者距离公式作为次要排序条件为宜。(方差为0说明为同种颜色,再次前提下欧式距离越大明暗差别越大),本段描述下面绘制程序。
figure % 0-1对应的为0-255
p=plot(1,1,'o','LineWidth',100);%方差为0
set(p,'color',[0.6 0.6 0.6]);
hold on
p=plot(2,1,'o','LineWidth',100);%标准点用于对比
set(p,'color',[0.5 0.5 0.5]);
p=plot(3,1,'o','LineWidth',100);
set(p,'color',[0.5 0.6732 0.5]);%方差不为0,欧氏距离与第一个点一致
axis([0,4,0,2])
然而在第一问中,附件2和附件3中如果按上述排序方式选择近似颜色,就会发现,欧式距离过大,但是方差很小,颜色深浅差距很大,因此我们可以设置权重以平衡这两个公式。同样的我们可视化看下。

figure% 0-1 对应的为0-255
p=plot(1,1,'o','LineWidth',100);%方差为0
set(p,'color',[0.6 0.6 0.6]);
hold on
p=plot(2,1,'o','LineWidth',100);%标准点用于对比
set(p,'color',[0.5 0.5 0.5]);
p=plot(3,1,'o','LineWidth',100);
set(p,'color',[0.5 0.54 0.5]);%方差不为0,欧氏距离与第一个点一致
axis([0,4,0,2])
从效果来看还可以接受,两个结果的欧式距离分别是0.1732和0.05,因此我们可以将差的方差和欧式距离公式权重比例设为0.776:0.224,我们新构建的距离公式应当为
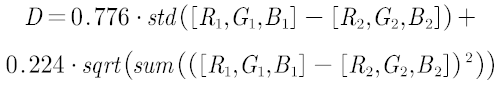
权重可以根据各自认为的颜色近似自行设置,这里只是给了一个案例
对于第二问,这个表现力就是说能够近似体现多种颜色,优先增加与多个颜色差别较小,不管增加几种颜色,但本质上还是选近似颜色,只不过同时多增加几种颜色就要考虑新聚类中心的分布问题,FCM思想比较适合解决该问题,目标函数可以就以FCM的来
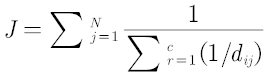
其中i表示聚类中心,j表示其他点,c为聚类中心总数,N为其他点总数,(别去管什么隶属度矩阵,你们直接用上面函数就行,除了FCM也可以借助其他聚类算法的思想来做)
该算法思想就是其他点到聚类中心的距离的倒数之和最小,但是别直接套用该算法程序,其中的距离公式需要更改。第二问说是从技术革新的角度,那么本问被聚类的点应当为256*256*256个点了,并不是附件2和附件3的点来做聚类分析,当然在选出新聚类中心颜色后,可以再去算一附件2和附件3的J函数值,对于题目提到的表现力,颜色越近似就说明表现力越好,表现力函数公式可以直接是J函数的倒数。
本文的程序设计思路可以做个参考:
1.两个自变量,除了固定的22个颜色外额外增加的颜色数、聚类范围(切记不是半径为R的圆形)
2.(优化算法)随机产生n个个体,每个个体拥有m个新聚类中心(m个RGB值,看做是三维坐标)和1个聚类范围,被聚类的点就是256*256*256个点,按第一问距离公式计算各聚类中心距离。
3.设立目标函数J,如果想将表现力设为目标函数,这里目标函数就设为1/J。(第一问两个公式加权聚合为一个公式,权重自行设立,效果不好就调试下),求J函数最小化或者1/J函数最大化。
4.迭代多次后,输出新增最佳m个颜色RGB。
第三问,在上一问基础上考虑成本,成本函数就按新增了多少个颜色来算,相当于说本问寻优的自变量个数m是变化的,可以在上述步骤增加一个目标函数M,即新增m个颜色。本问即是多目标寻优问题。可以去看下之前我发的推文(推文路径:算法-优化算法-智能优化算法函数寻优补充篇),专门举了自变量个数变化的寻优案例程序,以及多目标常用排序方法(推文路径:算法-优化算法-非支配排序-Ⅱ),就自己去
本文链接:http://zhangshiyu.com/post/18367.html