第一章 函数与极限
第一节 映射与函数
一、映射
f从x到y的映射: f : X → Y f:X→Y f:X→Y,x是原像,y是像。函数中x是自变量,y是因变量。
映射三要素:
集合X,定义域 D = D f = X D=D_f=X D=Df=X
集合Y,值域 R f = f ( D ) = f ( X ) = { f ( x ) ∣ x ∈ X } = { y ∣ y = f ( x ) , x ∈ D } , R f ⊆ Y R_f=f(D)=f(X)=\{f(x)|x∈X\}=\{y|y=f(x),x∈D\},R_f⊆Y Rf=f(D)=f(X)={f(x)∣x∈X}={y∣y=f(x),x∈D},Rf⊆Y,教材上用的是 ⊂ \subset ⊂
对应法则 f f f
满射:Y全部用完
单射:x和y一 一对应,但Y不一定用完。
一 一映射(双射):满射+单射。
映射,算子,泛函,变换,函数(实数集X→实数集Y)。
逆映射:
f : X → Y f:X→Y f:X→Y
g : R f → X g:R_f→X g:Rf→X
g = f − 1 g=f^{-1} g=f−1
定义域: D f − 1 = R f D_{f^{-1}}=R_f Df−1=Rf
值域: R f − 1 = X R_{f^{-1}}=X Rf−1=X
mathmatica求反函数,优先使用方法2
方法1:
ClearAll["Global`*"];(*定义函数*)f[x_] := x + 1;(*使用 InverseFunction*)inverse = InverseFunction[f]
方法2:
ClearAll["Global`*"];(*定义函数*)f[x_] := x + 1;(*求反函数*)inverse = x /. Solve[y == f[x], x][[1]]
复合映射:
设有两个映射: g : X → Y 1 , f : Y 2 → Z g:X→Y_1,f:Y_2→Z g:X→Y1,f:Y2→Z
f ∘ g = f [ g ( x ) ] f \circ g=f[g(x)] f∘g=f[g(x)], R g ⊆ D f R_g⊆D_f Rg⊆Df,教材上用的是 ⊂ \subset ⊂,满足结合律,不满足交换律
二、函数
绝对值函数、符号函数、取整函数、狄利克雷函数
函数的几种特性:
有界性、单调性、奇偶性、周期性、凹凸性
初等函数:幂指对,三反三
双曲正弦、双曲余弦、双曲正切
反双曲正弦、反双曲余弦、反双曲正切
y = x + 2 + 1 y=\sqrt{x+2}+1 y=x+2 +1,求定义域和值域
(*求定义域,需要程序员构造不等式*)domain = Reduce[x + 2 >= 0, x, Reals];domain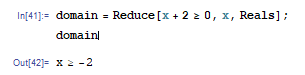
(*求值域*)y = Sqrt[x + 2] + 1;range = FunctionRange[y, x, y];rangemathematica 8.0不支持,暂无输出结果。
第二节 数列的极限
一、数论极限的定义
lim n → ∞ x n = a ⇔ ∀ ε > 0 , ∃ 正整数 N ,当 n > N 时,有 ∣ x n − a ∣ < ε \lim_{n \to \infty} x_n= a\Leftrightarrow \forall \varepsilon>0, \exists 正整数N,当n>N时,有|x_n-a|<\varepsilon n→∞limxn=a⇔∀ε>0,∃正整数N,当n>N时,有∣xn−a∣<ε
二、收敛数列的性质
1.极限唯一。
2.收敛必有界,反之不一定成立。
3.收敛数列的保号性: 如果 lim n → ∞ x n = a 且 a > 0 ( 或 a < 0 ) ,那么存在正整数 N ,当 n > N 时,都有 x n > 0 ( x n < 0 ) 如果\lim_{n \to \infty} x_n= a且a>0(或a<0),那么存在正整数N,当n>N时,都有x_n>0(x_n<0) 如果n→∞limxn=a且a>0(或a<0),那么存在正整数N,当n>N时,都有xn>0(xn<0)
4.原数列收敛,那么子数列也收敛,反之不一定成立。
第三节 函数的极限
一、函数极限的定义
自变量趋于有限值时函数的极限:
lim x → x 0 f ( x ) = A ⇔ ∀ ε > 0 , ∃ δ > 0 ,当 0 < ∣ x − x 0 ∣ < δ 时,有 ∣ f ( x ) − A ∣ < ε \lim_{x \to x_0} f(x)= A\Leftrightarrow \forall \varepsilon>0, \exists\delta>0,当0<|x-x_0|<\delta时,有|f(x)-A|<\varepsilon x→x0limf(x)=A⇔∀ε>0,∃δ>0,当0<∣x−x0∣<δ时,有∣f(x)−A∣<ε
自变量趋于无穷大时函数的极限:
lim x → ∞ f ( x ) = A ⇔ ∀ ε > 0 , ∃ X > 0 ,当 ∣ x ∣ > X 时,有 ∣ f ( x ) − A ∣ < ε \lim_{x \to \infty} f(x)= A\Leftrightarrow \forall \varepsilon>0, \exists X>0,当|x|>X时,有|f(x)-A|<\varepsilon x→∞limf(x)=A⇔∀ε>0,∃X>0,当∣x∣>X时,有∣f(x)−A∣<ε
二、函数极限的性质,跟数列极限类似
1.极限唯一性
2.局部有界性
3.局部保号性
4.函数收敛,其数列也收敛
第四节 无穷小和无穷大
自然智慧即可。
第五节 极限运算法则
自然智慧即可。
第六节 极限存在准则 两个重要极限
极限存在准则:
1.夹逼准则
2.单调有界数列必有极限。单调有界是充分条件。
柯西极限存在准则,也叫柯西申敛原理。
数列 { x n } \{x_n\} {xn}收敛的充分必要条件是:对于任意给定的正数 ε \varepsilon ε,存在正整数 N N N,使得当 m > N m>N m>N, n > N n>N n>N,有 ∣ x n − x m ∣ < ε |x_n-x_m|<\varepsilon ∣xn−xm∣<ε
两个重要极限:
lim x → 0 s i n x x = 1 \lim_{x \to 0} \frac{sin x}{x}=1 x→0limxsinx=1
lim x → ∞ ( 1 + 1 x ) x = e \lim_{x \to \infty}( 1+\frac{1}{x})^x=e x→∞lim(1+x1)x=e
mathmatica求极限:
Limit[(1 + 1/x)^x, x -> Infinity]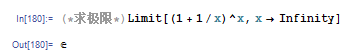
第七章 无穷小的比较
高阶无穷小
低阶无穷小
同阶无穷小、等价无穷小
k阶无穷小
求极限的时候, f ( x ) + g ( x ) f(x)+g(x) f(x)+g(x), f ( x ) f(x) f(x)不能用等价无穷小替换。 f ( x ) ∗ g ( x ) f(x)*g(x) f(x)∗g(x), f ( x ) f(x) f(x)可以用等价无穷小替换。
第八章 函数的连续性与间断点
一、函数的连续性
左右极限相等并且极限等于函数值,那就是连续。
二、函数的间断点
第一类间断点(有极限):可去间断点、跳跃间断点。
第二类间断点(没有极限):无穷间断点(y趋于无穷)、振荡间断点。
第九节 连续函数的运算与初等函数的连续性
第十节 闭区间上连续函数的性质
f ( x ) f(x) f(x)连续,定义域是 [ a , b ] [a,b] [a,b]。两端点的值是 f ( a ) = A f(a)=A f(a)=A和 f ( b ) = B f(b)=B f(b)=B
1.有界性
值域在一个闭区间里。
2.零点定理与介值定理
零点定理: f ( a ) f(a) f(a)和 f ( b ) f(b) f(b)异号,即使 f ( a ) ∗ f ( b ) < 0 f(a)*f(b)<0 f(a)∗f(b)<0,则在开区间 ( a , b ) (a,b) (a,b)内至少有一点 ξ \xi ξ,使 f ( ξ ) = 0 f(\xi)=0 f(ξ)=0。
介值定理: f ( a ) = A f(a)=A f(a)=A, f ( b ) = B f(b)=B f(b)=B,对于 A A A与 B B B之间的任意一个数 C C C,在开区间 ( a , b ) (a,b) (a,b)内至少有一点 ξ \xi ξ,使 f ( ξ ) = C f(\xi)=C f(ξ)=C。
3.一致连续性
定义:设函数 f ( x ) f(x) f(x)在区间I上有定义,如果对于任意给定的正数 ε \varepsilon ε,总存在正数 δ \delta δ,使得对于区间I上的任意两点 x 1 x_1 x1, x 2 x_2 x2,当 ∣ x 1 − x 2 ∣ < δ |x_1-x_2|<\delta ∣x1−x2∣<δ 时,有 ∣ f ( x 1 ) − f ( x 2 ) ∣ < ε |f(x_1)-f(x_2)|<\varepsilon ∣f(x1)−f(x2)∣<ε,那么称函数 f ( x ) f(x) f(x)在区间I上一致连续。
一致连续性定理:如果函数 f ( x ) f(x) f(x)在闭区间 [ a , b ] [a,b] [a,b]上连续,那么它在该区间上一致连续。
第二章 导数与微分
第一节 导数概念
一、引例
瞬时变化率
切线
二、导数的定义
Δ x = x − x 0 \Delta x=x-x_0 Δx=x−x0, Δ y = f ( x ) − f ( x 0 ) = f ( x 0 + Δ x ) − f ( x 0 ) \Delta y=f(x)-f(x_0)=f(x_0+\Delta x)-f(x_0) Δy=f(x)−f(x0)=f(x0+Δx)−f(x0)
f ′ ( x 0 ) = lim Δ x → 0 Δ y Δ x = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f^{'}(x_0)=\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}=\lim_{\Delta x \to 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} f′(x0)=Δx→0limΔxΔy=Δx→0limΔxf(x0+Δx)−f(x0)
f ′ ( x 0 ) = y ′ ∣ x = x 0 = d y d x ∣ x = x 0 = d f ( x ) d x ∣ x = x 0 f^{'}(x_0)=y^{'}|_{x=x_0}=\frac{dy}{dx}|_{x=x_0}=\frac{df(x)}{dx}|_{x=x_0} f′(x0)=y′∣x=x0=dxdy∣x=x0=dxdf(x)∣x=x0
三、导数的切线意义
过点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)切线方程: y − y 0 = f ′ ( x 0 ) ( x − x 0 ) y-y_0=f^{'}(x_0)(x-x_0) y−y0=f′(x0)(x−x0)
过点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)法线方程: y − y 0 = − 1 f ′ ( x 0 ) ( x − x 0 ) y-y_0=-\frac{1}{f^{'}(x_0)}(x-x_0) y−y0=−f′(x0)1(x−x0)
四、函数可导性与连续性的关系
连续不一定可导。可导必连续。
第二节 函数的求导法则
一、函数的和、差、积、商的求导法则
1. ( u ± v ) ′ = u ′ ± v ′ (u\pm v)^{'}=u^{'}\pm v^{'} (u±v)′=u′±v′
2. ( u v ) ′ = u ′ v + u v ′ (uv)^{'}=u^{'}v+uv^{'} (uv)′=u′v+uv′
3. ( u v ) ′ = u ′ v − u v ′ v 2 (\frac{u}{v})^{'}=\frac{u^{'}v-uv^{'}}{v^2} (vu)′=v2u′v−uv′
二、反函数的求导法则
[ f − 1 ( x ) ] ′ = 1 f ′ ( y ) [f^{-1}(x)]^{'}=\frac{1}{f^{'}(y)} [f−1(x)]′=f′(y)1或 d y d x = 1 ( d x d y ) \frac{dy}{dx}=\frac{1}{(\frac{dx}{dy})} dxdy=(dydx)1
三、复合函数的求导法则
y = f ( u ) y=f(u) y=f(u), u = g ( x ) u=g(x) u=g(x),y对x求导:
d y d x = f ′ ( u ) ∗ g ′ ( x ) \frac{dy}{dx}=f^{'}(u)*g^{'}(x) dxdy=f′(u)∗g′(x) 或 d y d x = d y d u ∗ d u d x \frac{dy}{dx}=\frac{dy}{du}*\frac{du}{dx} dxdy=dudy∗dxdu
四、基本求导法则与导数公式
暂无
mathematica求导
ClearAll["Global`*"];f[x_] := x^2 + 3*x + 5;derivative = D[f[x], x]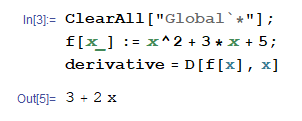
第三节 高阶导数
1. ( u ± v ) ( n ) = u ( n ) ± v ( n ) (u\pm v)^{(n)}=u^{(n)}\pm v^{(n)} (u±v)(n)=u(n)±v(n)
2.莱布尼茨公式:
( u v ) ( n ) = ∑ k = 0 n C n k u ( n − k ) v ( k ) (uv)^{(n)}=\sum_{k=0}^nC_{n}^{k}u^{(n-k)}v^{(k)} (uv)(n)=k=0∑nCnku(n−k)v(k)
mathematica求二阶导
ClearAll["Global`*"];h[x_] := Sin[x];secondDerivative = D[h[x], {x, 2}] (* 二阶导数 *)
第四节 隐函数及由参数方程所确定的函数的导数 相关变化率
一、隐函数的导数
F ( x , y ) = x + y 3 − 1 = 0 F(x,y)=x+y^3-1=0 F(x,y)=x+y3−1=0,对x求导,y是对x的中间函数: 1 + 3 y 2 y ′ = 0 → y ′ = − 1 3 y 2 1+3y^{2} y^{'}=0→y^{'}=-\frac{1}{3y^2} 1+3y2y′=0→y′=−3y21
mathematica对隐函数求导
ClearAll["Global`*"];(*定义隐函数*)F[x_, y_] := x + y^3 - 1(*进行隐式求导*)implicitDerivative = D[F[x, y], x] + D[F[x, y], y]*Derivative[1][y][x] == 0(*解出 y'=dy/dx*)solution = Solve[implicitDerivative, Derivative[1][y][x]](*提取 dy/dx*)dy_dx = Derivative[1][y][x] /. solution // Simplify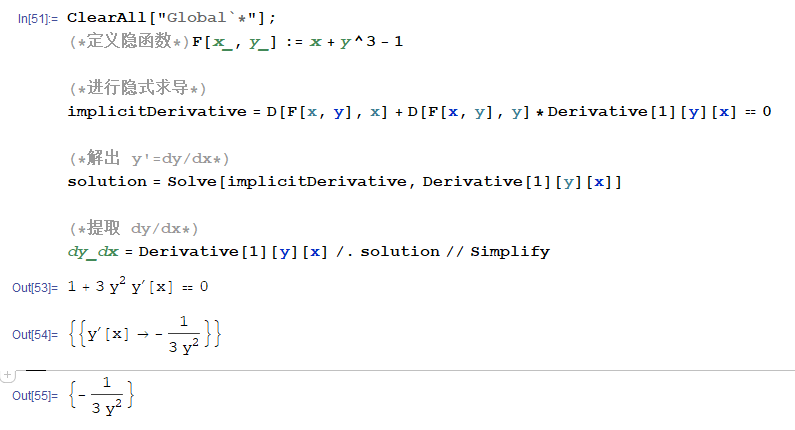
二、由参数方程所确定的函数的导数
参数方程: { x = φ ( t ) y = ψ ( t ) \begin{cases} x = \varphi(t) \\y = \psi(t) \end{cases} {x=φ(t)y=ψ(t)
求导法则: d y d x = ( d y d t ) ( d x d t ) = ψ ′ ( t ) φ ′ ( t ) \frac{dy}{dx}=\frac{(\frac{dy}{dt})}{(\frac{dx}{dt})}=\frac{\psi^{'}(t)}{ \varphi^{'}(t)} dxdy=(dtdx)(dtdy)=φ′(t)ψ′(t)
mathematica对参数方程求导:
ClearAll["Global`*"];x[t_] := t^2;y[t_] := t^3;dxdt = D[x[t], t]; (*对 x(t) 求导*)dydt = D[y[t], t];(*对 y(t) 求导*)slope = dydt/dxdt
三、相关变化率
无
第五节 函数的微分
一、微分的定义
二、微分的几何意义
三、基本初等函数的微分公式与微分运算法则
跟求导一样
四、微分在近似计算中的应用
f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) f(x)\approx f(x_0)+f^{'}(x_0)(x-x_0) f(x)≈f(x0)+f′(x0)(x−x0),其中 f ( x 0 ) f(x_0) f(x0)、 f ′ ( x 0 ) f^{'}(x_0) f′(x0)、 x − x 0 x-x_0 x−x0计算方便
第三章 微分中值定理与导数的应用
第一节 微分中值定理
一、罗尔定理
导数为0的点被称为驻点(稳定点、临界点)。
费马引理:设函数 f ( x ) f(x) f(x)在点 x 0 x_0 x0的某邻域 U ( x 0 ) U(x_0) U(x0)内有定义,并且在 x 0 x_0 x0处可导,如果对任意的 x ∈ U ( x 0 ) x∈U(x_0) x∈U(x0),有
f ( x ) ⩽ f ( x 0 ) f(x)\leqslant f(x_0) f(x)⩽f(x0) (或 f ( x ) ⩾ f ( x 0 ) f(x)\geqslant f(x_0) f(x)⩾f(x0)),
那么 f ′ ( x 0 ) = 0 f^{'}(x_0)=0 f′(x0)=0。
罗尔定理:如果函数 f ( x ) f(x) f(x)满足
1.在闭区间 [ a , b ] [a,b] [a,b]上连续;
2.在开区间 ( a , b ) (a,b) (a,b)内可导;
3.在区间端点处的函数值相等,即 f ( a ) = f ( b ) f(a)=f(b) f(a)=f(b),
那么在 ( a , b ) (a,b) (a,b)内至少有一点 ξ ( a < ξ < b ) ξ(a<ξ<b) ξ(a<ξ<b),使得 f ′ ( ξ ) = 0 f'(ξ)= 0 f′(ξ)=0。
二、拉格朗日中值定理
如果函数 f ( x ) f(x) f(x)满足
1.在闭区间 [ a , b ] [a,b] [a,b]上连续;
2.在开区间 ( a , b ) (a,b) (a,b)内可导;
那么在 ( a , b ) (a,b) (a,b)内至少有一点 ξ ( a < ξ < b ) ξ(a<ξ<b) ξ(a<ξ<b),是等式
f ( b ) − f ( a ) = f ′ ( ξ ) ( b − a ) f(b)-f(a)=f'(ξ)(b-a) f(b)−f(a)=f′(ξ)(b−a)
成立。
这个定理也叫有限增量定理,微分中值定理。
有限增量公式: Δ y = f ′ ( x + θ Δ x ) ∙ Δ x ( 0 < θ < 1 ) \Delta y=f'(x+θ\Delta x)\bullet\Delta x (0<θ<1) Δy=f′(x+θΔx)∙Δx(0<θ<1)
三、柯西中值定理
如果函数 f ( x ) f(x) f(x)及 F ( x ) F(x) F(x)满足
1.在闭区间 [ a , b ] [a,b] [a,b]上连续;
2.在开区间 ( a , b ) (a,b) (a,b)内可导;
3.在任一 x ∈ ( a , b ) x∈(a,b) x∈(a,b), F ′ ( x ) ≠ 0 F'(x)\neq0 F′(x)=0,
f ( b ) − f ( a ) F ( b ) − F ( a ) = f ′ ( ξ ) F ′ ( ξ ) \frac{f(b)-f(a)}{F(b)-F(a)}=\frac{f'(ξ)}{F'(ξ)} F(b)−F(a)f(b)−f(a)=F′(ξ)f′(ξ)
成立。
第二节 洛必达法则
0 0 \frac{0}{0} 00或 ∞ ∞ \frac{∞}{∞} ∞∞
第三节 泰勒公式
泰勒公式: f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + ⋅ ⋅ ⋅ + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + R n ( x ) f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+⋅⋅⋅+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x) f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+⋅⋅⋅+n!f(n)(x0)(x−x0)n+Rn(x)
佩亚诺余项: R n ( x ) = o ( ( x − x 0 ) n ) R_n(x)=o((x-x_0)^n) Rn(x)=o((x−x0)n)
拉格朗日余项: R n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 R_n(x)=\frac{f^{(n+1)}(ξ)}{(n+1)!}(x-x_0)^{n+1} Rn(x)=(n+1)!f(n+1)(ξ)(x−x0)n+1,其中 ξ ξ ξ是 x 0 x_0 x0与 x x x之间的某个值。
麦克劳林公式,当 x = x 0 x=x_0 x=x0时: f ( x ) = f ( 0 ) + f ′ ( 0 ) x + f ′ ′ ( 0 ) 2 ! x 2 + ⋅ ⋅ ⋅ + f ( n ) ( 0 ) n ! x n + o ( x n ) f(x)=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+⋅⋅⋅+\frac{f^{(n)}(0)}{n!}x^n+o(x^n) f(x)=f(0)+f′(0)x+2!f′′(0)x2+⋅⋅⋅+n!f(n)(0)xn+o(xn)
初等函数的麦克劳林公式
暂无
mathematica计算麦克劳林公式:
ClearAll["Global`*"];f[x_] := Sin[x ]; (*定义函数*)maclaurinSeries = Series[f[x], {x, 0, 5}] (*计算麦克劳林级数*)
第四节 函数的单调性与曲线的凹凸性
第五节 函数的极值与最大值最小值
第六节 函数图形的描绘
五个步骤
第七节 曲率
一、弧微分
弧微分公式: d s = 1 + ( y ′ ) 2 d x ds=\sqrt{1+(y')^{2}}dx ds=1+(y′)2 dx
二、曲率及其计算公式
K = ∣ d α d s ∣ K=|\frac{dα}{ds}| K=∣dsdα∣, α α α是倾斜角, s s s是弧段长度。
K = ∣ y ′ ′ ∣ ( 1 + ( y ′ ) 2 ) 3 / 2 K=\frac{|y''|}{(1+(y')^2)^{3/2}} K=(1+(y′)2)3/2∣y′′∣
对于圆: K = 1 r K=\frac{1}{r} K=r1
参数方程: { x = φ ( t ) y = ψ ( t ) \begin{cases} x = \varphi(t) \\y = \psi(t) \end{cases} {x=φ(t)y=ψ(t)
K = ∣ φ ′ ( t ) ψ ′ ′ ( t ) − φ ′ ′ ( t ) ψ ′ ( t ) ∣ [ ( φ ′ ) 2 ( t ) + ψ ′ ) 2 ( t ) ] 3 / 2 K=\frac{|\varphi^{'}(t)\psi^{''}(t)-\varphi^{''}(t)\psi^{'}(t)|}{ [(\varphi^{'})^2(t)+\psi^{'})^2(t)]^{3/2}} K=[(φ′)2(t)+ψ′)2(t)]3/2∣φ′(t)ψ′′(t)−φ′′(t)ψ′(t)∣
三、曲率圆与曲率半径
曲率圆:在曲线上点M做法线,在凹侧 1 K = ρ \frac{1}{K}=\rho K1=ρ 作为圆心,这个元会过 M M M点。圆心是曲率中心,半径 ρ \rho ρ是曲率半径。
四、曲率中心的计算公式 渐曲线和渐伸线
曲线C上的点 ( x , f ( x ) ) (x,f(x)) (x,f(x))
曲率中心 D ( α , β ) D(\alpha,\beta) D(α,β)的坐标: { α = x − y ′ ( 1 + ( y ′ ) 2 ) y ′ ′ β = y + 1 + ( y ′ ) 2 y ′ ′ \begin{cases} \alpha=x-\frac{y'(1+(y')^2)}{y''}\\\beta=y+\frac{1+(y')^2}{y''} \end{cases} {α=x−y′′y′(1+(y′)2)β=y+y′′1+(y′)2
点 ( x , f ( x ) ) (x,f(x)) (x,f(x))在曲线C上移动,这是渐伸线。
曲率中心 D ( α , β ) D(\alpha,\beta) D(α,β)的坐标会根据点 ( x , f ( x ) ) (x,f(x)) (x,f(x))在曲线C上移动,这是渐曲线。
第八节 方程的近似解
一、二分法
二、切线法
x 1 = x 0 − f ( x 0 ) f ′ ( x 0 ) x_1=x_0-\frac{f(x_0)}{f'(x_0)} x1=x0−f′(x0)f(x0)
三、割线法
割线法也叫弦截法。
x n + 1 = x n − x n − x n − 1 f ( x n ) − f ( x n − 1 ) x_{n+1}=x_n-\frac{x_n-x_{n-1}}{f(x_n)-f(x_{n-1})} xn+1=xn−f(xn)−f(xn−1)xn−xn−1
第四章 不定积分
第一节 不定积分的概念
一、原函数与不定积分的概念
原函数存在定理:连续函数一定有原函数。
mathematica求函数的不定积分:
ClearAll["Global`*"];f[x_] := x^2;indefiniteIntegralWithConstant = Integrate[f[x], x] + C (*C是常数,代表积分常数*)
二、基本积分表
表后期补上
三、不定积分的性质
第二节 换元积分法
一、第一类换元积分法
u = φ ( x ) u=\varphi(x) u=φ(x)
∫ f [ φ ( x ) ] ∗ φ ′ ( x ) = ∫ f ( u ) d u \int f[\varphi(x)]*\varphi'(x)=\int f(u)du ∫f[φ(x)]∗φ′(x)=∫f(u)du
二、第二类换元积分法
x = φ ( t ) x=\varphi(t) x=φ(t),需要求反函数 t = φ − 1 ( x ) t=\varphi^{-1}(x) t=φ−1(x)
∫ f ( x ) d x = ∫ f [ φ ( t ) ] φ ′ ( t ) d t \int f(x)dx=\int f[\varphi(t)]\varphi'(t)dt ∫f(x)dx=∫f[φ(t)]φ′(t)dt
第三节 分部积分法
∫ u v ′ d x = u v − ∫ u ′ v d x \int uv'dx=uv-\int u'vdx ∫uv′dx=uv−∫u′vdx
或者
∫ u d v = u v − ∫ v d u \int udv=uv-\int vdu ∫udv=uv−∫vdu
第四节 有理函数的积分
有理函数: P ( x ) Q ( x ) \frac{P(x)}{Q(x)} Q(x)P(x),其中 P ( x ) P(x) P(x)和 Q ( x ) Q(x) Q(x)都是多项式。
Q ( x ) Q(x) Q(x)是二次时,令 Q ( x ) = 0 Q(x)=0 Q(x)=0,求出两个根。
如果两个根不一样,可拆分母。
如果两个根一样,令 u = x − x 0 u=x-x_0 u=x−x0换元。
如果不存在,分母转换成 ( x + a ) 2 + b (x+a)^2+b (x+a)2+b。
二、可化为有理函数的积分举例
第五节 积分表的使用
第五章 定积分
第一节 定积分得概念与性质
一、定积分问题举例
二、定积分的定义
三、定积分的近似计算
四、定积分的性质
定积分中值定理:如果函数 f ( x ) f(x) f(x)在积分区间 [ a , b ] [a,b] [a,b]上连续,那么在 [ a , b ] [a,b] [a,b]上至少存在一个点 ξ ξ ξ,使下式成立:
∫ a b f ( x ) d x = f ( ξ ) ( b − a ) \int_a^b f(x)dx=f(ξ)(b-a) ∫abf(x)dx=f(ξ)(b−a) ,其中 ( a ⩽ ξ ⩽ b ) (a⩽ξ⩽b) (a⩽ξ⩽b)
第二节 微积分基本公式
三、牛顿-莱布尼茨公式
∫ a b f ( x ) d x = F ( b ) − F ( a ) \int_a^b f(x)dx=F(b)-F(a) ∫abf(x)dx=F(b)−F(a)
mathematica求定积分:
ClearAll["Global`*"];f[x_] := x^2;Integrate[f[x], {x, 0, 2}]
第三节 定积分的换元法和分部积分法
一、定积分的换元法
x = φ ( t ) x=φ(t) x=φ(t),注意积分的上限和下限:
∫ a b f ( x ) d x = ∫ α β f [ φ ( t ) ] φ ′ ( t ) d t \int_a^b f(x)dx=\int_α^β f[φ(t)]φ'(t)dt ∫abf(x)dx=∫αβf[φ(t)]φ′(t)dt
二、定积分的分部积分法
∫ a b u d v = [ u v ] a b − ∫ a b v d u \int_a^b udv=[uv]_a^b-\int_a^b vdu ∫abudv=[uv]ab−∫abvdu
第四节 反常积分
一、无穷限的反常积分
定义域包含无穷大
二、无界函数的反常积分
也叫瑕积分。值域无穷大或者震荡。
第五节 反常积分的审敛法 Γ \Gamma Γ函数
一、无穷限反常积分的审敛法
绝对收敛:如果 ∣ f ( x ) ∣ |f(x)| ∣f(x)∣收敛,那么 f ( x ) f(x) f(x)也收敛。
二、无界函数的反常积分的审敛法
三、 Γ \Gamma Γ函数
定义: Γ ( s ) = ∫ 0 + ∞ e − x x s − 1 d x \Gamma(s)=\int_0^{+∞}e^{-x}x^{s-1}dx Γ(s)=∫0+∞e−xxs−1dx,其中 s > 0 s>0 s>0
递推公式: Γ ( s + 1 ) = s Γ ( s ) \Gamma(s+1)=s\Gamma(s) Γ(s+1)=sΓ(s),其中 s > 0 s>0 s>0
余元公式:: Γ ( s ) Γ ( 1 − s ) = π sin π s \Gamma(s)\Gamma(1-s)=\frac{\pi}{\sin\pi s} Γ(s)Γ(1−s)=sinπsπ,其中 0 < s < 1 0<s<1 0<s<1
Γ ( 1 ) = 1 \Gamma(1)=1 Γ(1)=1
第六章 定积分的应用
第一节 定积分的元素法
第二节 定积分在几何学上的应用
一、平面图形的面积
直角坐标
极坐标:扇形面积
二、体积
旋转体
平行截面
三、平面曲线的弧长
暂无
第三节 定积分在物理学上的应用
第七章 微分方程
第一节 微分方程的基本概念
含导数的方程就是微分方程
第二节 可分离变量的微分方程
g ( y ) d y = f ( x ) d x g(y)dy=f(x)dx g(y)dy=f(x)dx,如果一阶方程能写成这个样子,就是可分离变量的微分方程。
第三节 齐次方程
一、齐次方程
d y d x = φ ( y x ) \frac{dy}{dx}=φ(\frac{y}{x}) dxdy=φ(xy),如果一阶微分方程能化成这种形式,就是齐次方程。
二、可化为齐次的方程
d y d x = a x + b y + c a 1 x + b 1 y + c 1 \frac{dy}{dx}=\frac{ax+by+c}{a_1x+b_1y+c_1} dxdy=a1x+b1y+c1ax+by+c,如果 c = c 1 = 0 c=c_1=0 c=c1=0是齐次的。否则不是齐次的,使用待定系数法可以转化成齐次的。
第四节 一阶线性微分方程
一、线性方程
一阶线性微分方程: d y d x + P ( x ) y = Q ( x ) \frac{dy}{dx}+P(x)y=Q(x) dxdy+P(x)y=Q(x)。如果 Q ( x ) ≡ 0 Q(x)≡0 Q(x)≡0,是齐次,否则不是齐次。
如果是齐次时: d y y = − P ( x ) d x \frac{dy}{y}=-P(x)dx ydy=−P(x)dx
二、伯努利方程
伯努利方程: d y d x + P ( x ) y = Q ( x ) y n \frac{dy}{dx}+P(x)y=Q(x)y^n dxdy+P(x)y=Q(x)yn,其中 n ≠ 0 , 1 n\neq0,1 n=0,1
通过变量代换,转成线性的。
第五节 可降阶的高阶微分方程
一、 y ( n ) = f ( x ) y^{(n)}=f(x) y(n)=f(x)型的微分方程
二、 y ′ ′ = f ( x , y ′ ) y''=f(x,y') y′′=f(x,y′)型的微分方程
三、 y ′ ′ = f ( y , y ′ ) y''=f(y,y') y′′=f(y,y′)型的微分方程
第六节 高阶线性微分方程
二、线性微分方程的解的结构
二阶齐次线性方程: y ′ ′ + P ( x ) y ′ + Q ( x ) y = 0 y''+P(x)y'+Q(x)y=0 y′′+P(x)y′+Q(x)y=0
线性相关、线性无关
第七节 常系数齐次线性微分方程
第八节 常系数非齐次线性微分方程
第九节 欧拉方程
欧拉方程: x n y ( n ) + p 1 x n − 1 y ( n − 1 ) + … + p n − 1 x y ′ + p n y = f ( x ) x^ny^{(n)}+p_1x^{n-1}y^{(n-1)}+…+p_{n-1}xy'+p_ny=f(x) xny(n)+p1xn−1y(n−1)+…+pn−1xy′+pny=f(x),其中 p 1 p_1 p1到 p n p_n pn为常数
第十节 常系数线性微分方程组解法举例
latex公式1
latex公式2