
文章目录
1.青蛙跳台阶专题2.汉诺塔专题希望读者们多多三连支持小编会继续更新你们的鼓励就是我前进的动力!书说上回,讲到了函数递归,迭代,这章 vlog 将针对递归迭代解决十分经典的两个问题
上一篇文章:https://blog.csdn.net/Zero_VPN/article/details/143168763?spm=1001.2014.3001.5502
1.青蛙跳台阶专题
题目介绍: 一共有 n 阶台阶,有一只青蛙能向上跳一阶台阶或两阶台阶
问:当青蛙跳到第n阶台阶时,有多少种跳法?
这个问题乍一看有些摸不着头脑,我们可以通过举例的方式来找到问题的规律
这里我们设青蛙跳上第 n 阶台阶有 Fib(n) 种方法
n = 1 时,青蛙跳上第 1 阶台阶的方法:1 种
n = 2 时,青蛙跳上第 2 阶台阶的方法:2 种
n = 3 时,青蛙跳上第 3 阶台阶的方法:3 种
n = 4 时,青蛙跳上第 4 阶台阶的方法:5 种
…
n = n-1 时,青蛙跳上第 n-1 阶台阶的方法:Fib(n-2)+Fib(n-3) 种
n = n 时,青蛙跳上第 n 阶台阶的方法:Fib(n-1)+Fib(n-2) 种
观察可得,本质上青蛙跳台阶问题实质上就是一个斐波那契数列
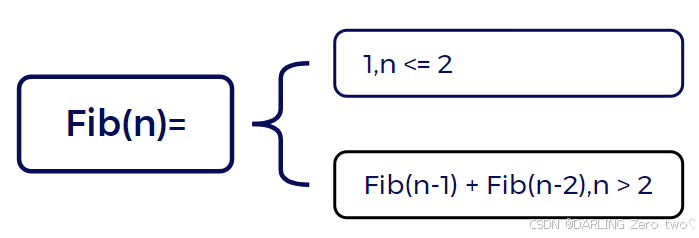
那么根据 vlog.8 中的斐波那契数列求和代码可以很容易写出解决方法:
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h> int Fib(int n){if (n == 1)return 1;else if (n == 2)return 2;elsereturn Fib(n - 1) + Fib(n - 2);} int main(){int x = 0; scanf("%d", &x);int ret = Fib(x);printf("Fib(%d)=%d\n", x, ret); return 0;}该代码在源代码的基础上只进行了略微修改,用的是递归的方法,同样的也可以用迭代的方法简化代码,减少内存占用,防止栈溢出的风险,详细请看上一篇vlog
2.汉诺塔专题
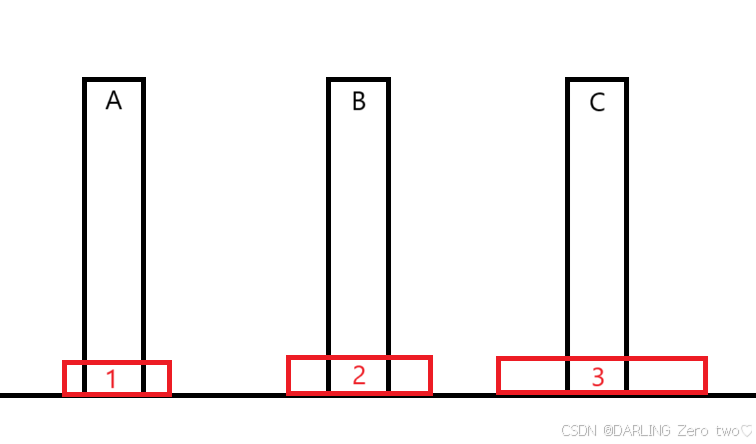
题目介绍:从左到右有A、B、C三个柱子,刚开始在A柱上从上到下套有1、2、3盘,其大小逐渐变大,盘子只能一个一个挪,借助于B柱,将A柱上的盘全部转移到C柱上,挪的过程中,盘子一定是上小下大
问:转移3个盘子需要多少步?
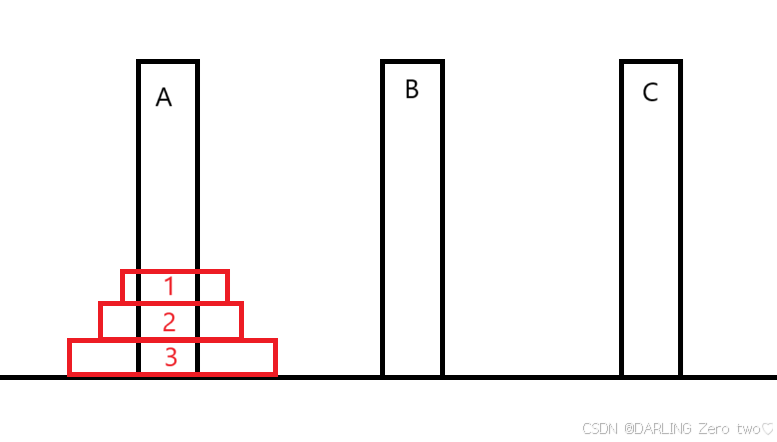
还是通过举例的方法,从三个盘子开始入手会更加简单的发现规律:
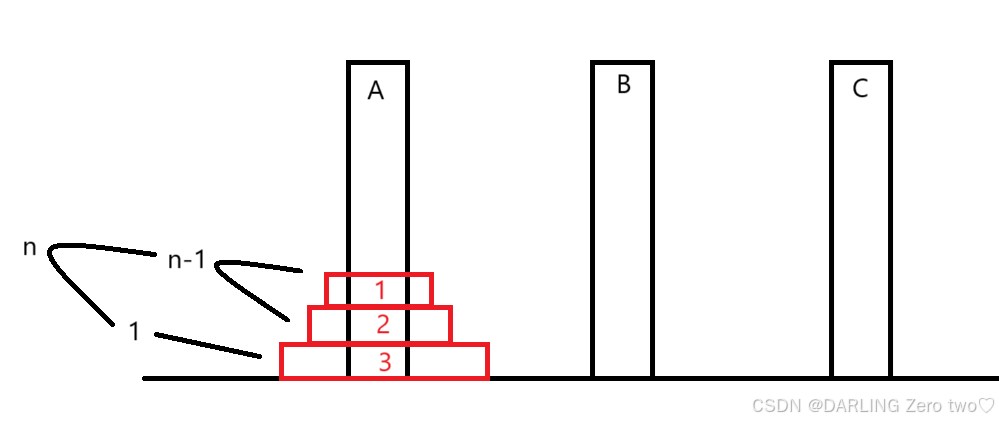
先把1盘挪到C柱,2盘挪到B柱,再把1盘挪回B柱,然后把3盘挪到C柱
即1、2盘为n-1个盘子
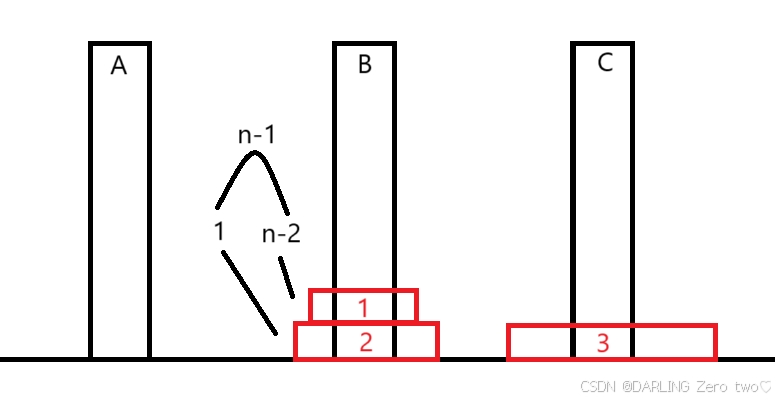
再接着把1盘挪到A柱
即1盘为n-2个盘子
最后把2盘放到C柱上,再把1盘放到C柱上
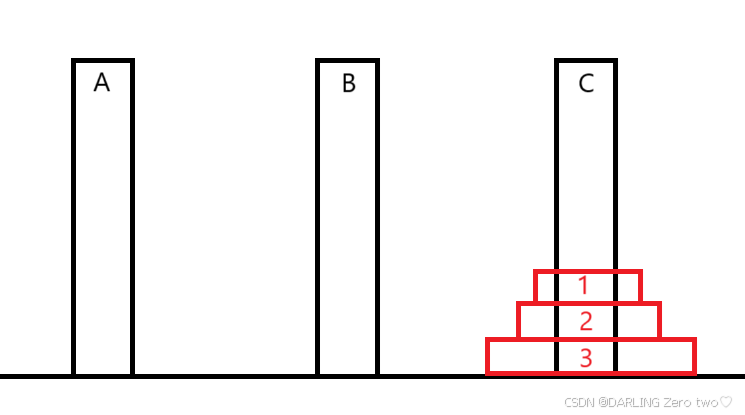
显而易见,这里移动了7次
我们定义移动的次数为F(n)
1 个盘子时,需要移动 1 次
2 个盘子时,需要移动 3 次
3 个盘子时,需要移动 7 次
4 个盘子时,需要移动 15 次
…
n-1 个盘子时,需要移动 2F(n-2) + 1 次
n 个盘子时,需要移动 2F(n-1) + 1 次
观察可得公式为 F(n) = 2F(n-1) + 1
那我们梳理一下过程可知
1、首先把n-1个盘子移动到第二根中转柱B上
2、再把最后一个也就是最大的那一个盘子移动到第三根目标柱C上
3、最后再把剩下的n-1个盘子移动到第三根目标柱C上
函数自己调用自己,那么可以知道这本质上也是个递归问题,写出以下移动过程代码:
#include<stdio.h>void move(char pos1, char pos2){printf(" %c->%c ", pos1, pos2);}void hanoi(int n, char pos1, char pos2, char pos3){if (n == 1) {move(pos1, pos3);}else{hanoi(n - 1, pos1, pos3, pos2);move(pos1, pos3);hanoi(n - 1, pos2, pos1, pos3);}}int main(){int n;scanf("%d", &n);hanoi(n, 'A', 'B', 'C');return 0;}可能看到这里会有些迷糊,其实只要理解了递归的思想,该问题也就迎刃而解了
有意思的是,在汉诺塔传说中,僧侣想要把64个金片同样从A柱转移到B柱
根据公式需要2^64-1次,在古印度那个时代这显然是不可能依靠人一个一个搬运完成的
如果还有不理解的可以点击文章开头的链接看我的上一篇 vlog 进行辅助知识理解 OwO
希望读者们多多三连支持
小编会继续更新
你们的鼓励就是我前进的动力!
