?博客主页:https://blog.csdn.net/2301_779549673
?欢迎点赞 ? 收藏 ⭐留言 ? 如有错误敬请指正!
?本文由 JohnKi 原创,首发于 CSDN?
?未来很长,值得我们全力奔赴更美好的生活✨


文章目录
?前言?️?二分查找的实现方式?️?1. 朴素的二分模板?️?2. 查找左端点的二分模板?️?3. 查找右端点的二分模板?总结
?前言
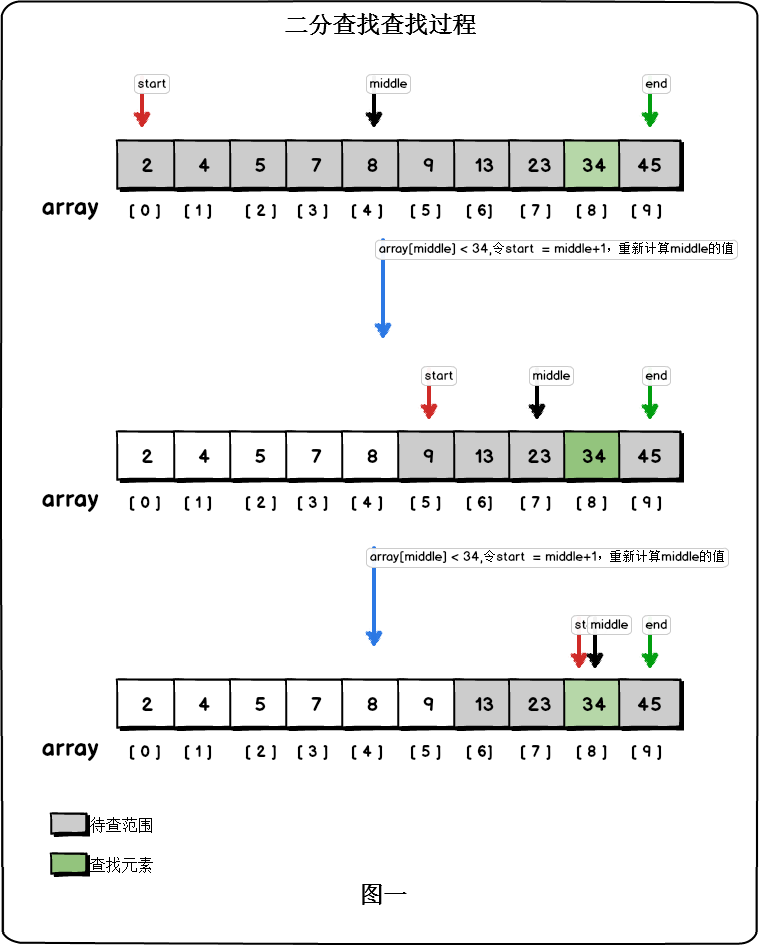
二分查找,也被称为折半查找,是一种在有序数组中高效查找目标元素的算法。它的基本思想是将待查找的区间不断地折半,通过比较中间元素与目标元素的大小关系,逐步缩小查找范围,直到找到目标元素或者确定目标元素不存在于数组中。
二分查找的优点在于其查找速度较快。在有序数组中,对于长度为 n 的数组,二分查找的时间复杂度为 O (log n)。相比之下,线性查找的时间复杂度为 O (n)。例如,在一个包含 1024 个元素的有序数组中,线性查找最坏情况下可能需要进行 1024 次比较,而二分查找最多只需要进行 10 次比较(log₂1024 = 10)。
?️?二分查找的实现方式
在二分查找中,二段性是一个非常重要的概念。
二段性指的是对于一个有序数组,存在一种性质,使得数组可以被划分为两个区间,满足在其中一个区间中性质成立,在另一个区间中性质不成立。
例如,对于一个升序排列的整数数组,要查找某个特定的整数 target。如果当前数组中的某个元素大于等于 target,那么可以认为这个元素以及它右边的部分处于一个区间,这个区间中的元素都大于等于 target;而这个元素左边的部分处于另一个区间,这个区间中的元素都小于 target。这就体现了二段性。
根据数学演算,每次取最中值的二分查找算法是时间复杂度最均匀和最好的,这在算法导论中有证明,但是太复杂了,就不在这说了
1. 确定查找方向
在二分查找过程中,通过判断当前中间元素与目标元素的大小关系,可以确定目标元素位于哪一个区间。如果中间元素小于目标元素,说明目标元素在中间元素右侧的区间;如果中间元素大于目标元素,说明目标元素在中间元素左侧的区间。2. 缩小查找范围
利用二段性,可以不断地将查找范围缩小一半。每次判断都能排除掉一半的区间,从而大大提高查找效率。例如,在一个有 100 个元素的有序数组中,使用二分查找最多只需要进行 7 次比较就可以找到目标元素,而如果采用顺序查找可能需要最多 100 次比较。?️?1. 朴素的二分模板
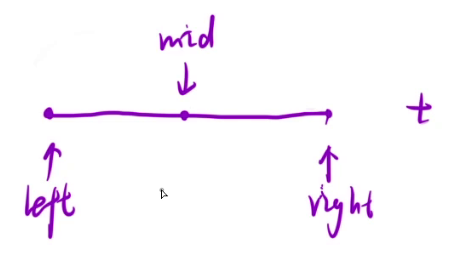
朴素的二分查找模板的查找效率其实可以说是最高的,因为它一旦遇到准确的值就会直接退出,但是这也为其添加了局限性,如果数组不存在指定值,或者需要查找的是一个区间的左值 or 右值,那么就很难实现
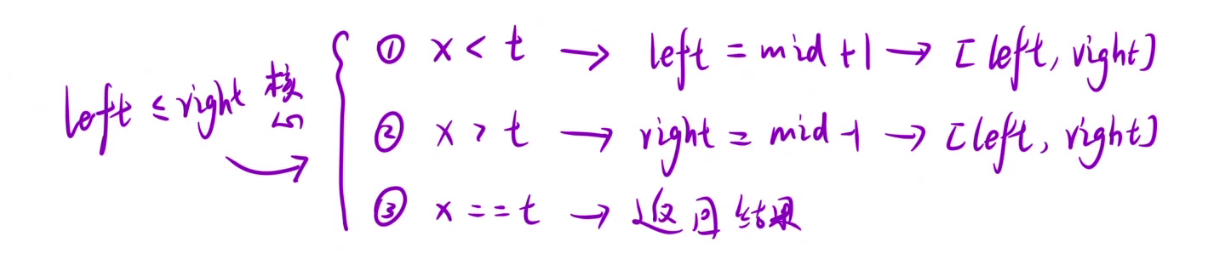
以题为例 链接: 704. 二分查找

这道题就可以用朴素二分查找来做,
设置循环条件:left <= rightmid = left + ((right - left) >> 1) : 查中间值(偶数时取左值),并设置防溢出设置 大于 小于 等于 的情况一旦 等于 返回值循环结束未找到,返回 -1class Solution {public: int search(vector<int>& nums, int target) { int left = 0, right = nums.size() - 1; while (left <= right) { int mid = left + ((right - left) >> 2); // 防止溢出 if(nums[mid] < target) left = mid + 1; else if(nums[mid] > target) right = mid -1; else return mid; } return -1; }};朴素二分模板总结

?️?2. 查找左端点的二分模板
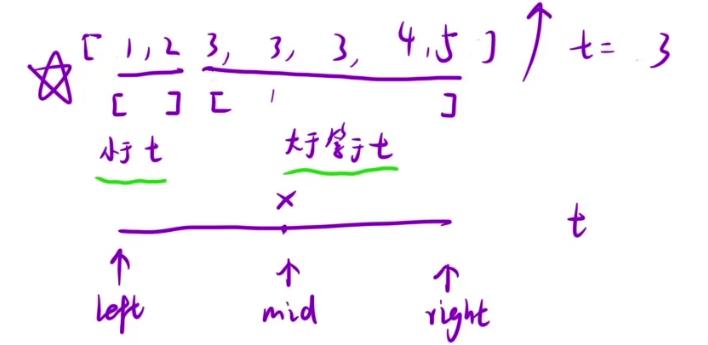
查找最左值时可以参考上图,我们需要找到一个值使其左边都是小于要查找的值的,右边包括其本身都是要大于等于要查找的值的,因此我们假设 [0, left) [right, end]为两个分区,那么我们就可以认为
1. 退出循环的值为 left < right
再然后我们因为要查找的值 如果 t >= nums[right] 那么代表他必然属于右边这个区间,因此,我们在设置 right 更新时,不能使其 right = mid - 1,而是
2. if(… >= …) right = mid
同理我们推导left,left 的最终所处位置其实应该和 right 一样,因为它往左的所有元素都是小于 t 的,因而 left 更新时
3. else left = mid + 1
最后我们需要确保循环不会一直下去,这就我们需要确保,当 left + 1 == right 时我们所查找的 mid 值。如果查右边,那么将一直进行 if(… >= …) right = mid 导致陷入死循环,所以
4. mid = left + ((right - left) >> 1))
最左值二分模板总结

?️?3. 查找右端点的二分模板
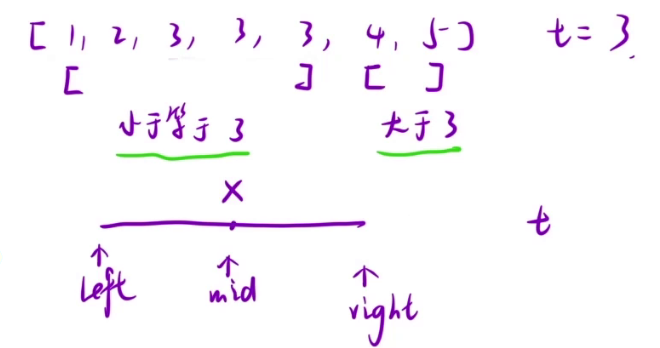
最右值其实和最左值的理解差不多,就是有 等于 的时候,left 不用超过mid,right 变成 mid - 1。
还有一个重要的点是,mid 的确定,因为 当 left + 1 == right 时我们所查找的 mid 值 为左值时,就会一直 if(… <= …) left = mid 陷入死循环,所以 mid = left + ((right - left + 1) >> 1))
最右值二分模板总结

以题为例 链接: 34. 在排序数组中查找元素的第一个和最后一个位置 - 同时解决左端点右端点问题
具体流程完完全全就是左右端点的模板,就不逐条解释了
vector<int> searchRange(vector<int>& nums, int target) { int left = 0, right = nums.size() - 1; vector<int> ret{-1, -1}; // 防止传入vector为空 if (nums.empty()) return ret; // 找左端点 while (left < right) { int mid = left + ((right - left) >> 1); if (nums[mid] < target) left = mid + 1; else right = mid; } if (nums[right] == target) ret[0] = right; right = nums.size() - 1; // 找右端点 while (left < right) { int mid = left + ((right - left + 1) >> 1); if (nums[mid] > target) right = mid - 1; else left = mid; } if (nums[left] == target) ret[1] = left; return ret; }?总结
本篇博文对 【算法】C++中的二分查找 做了一个较为详细的介绍,不知道对你有没有帮助呢
觉得博主写得还不错的三连支持下吧!会继续努力的~
