在数学建模中,我们拿到的数据经常会有缺失值,在缺失值不是很多的情况下,我们在数据预处理阶段会采用插值方法来将数据补齐,之后再开始我们的建模。
目录
1.Matlab 实现分段线性插值
2.拉格朗日插值多项式
3.牛顿(Newton)插值
编辑 4.埃尔米特(Hermite)插值
1.Matlab 实现分段线性插值
Matlab 中有现成的一维插值函数 interp1。
y=interp1(x0,y0,x,'method')
method 指定插值的方法,默认为线性插值。其值可为: 'nearest' 最近项插值, 'linear' 线性插值 'spline' 逐段 3 次样条插值, 'cubic' 保凹凸性 3 次插值。
所有的插值方法要求 x0 是单调的。
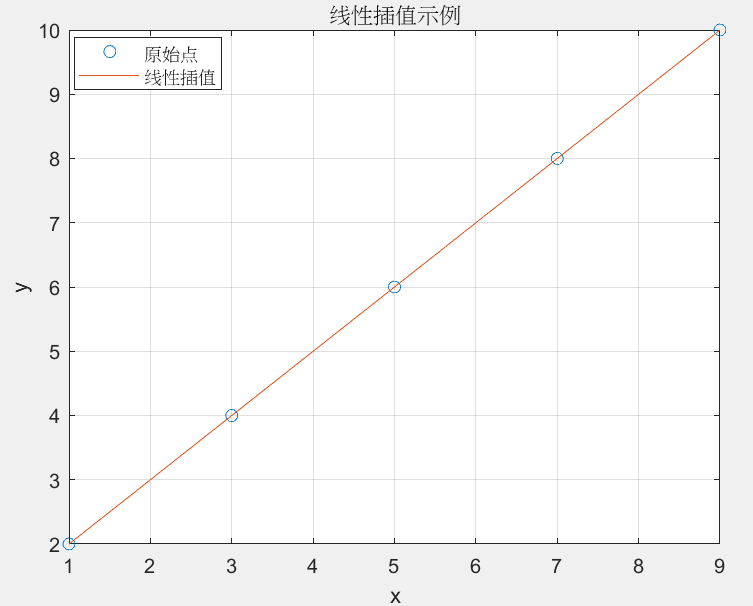
示例:
% 已知的点(x坐标和对应的y坐标) x = [1, 3, 5, 7, 9]; y = [2, 4, 6, 8, 10]; xi = 1:0.5:9; % 从1到9,步长为0.5 % 使用interp1函数进行线性插值 yi = interp1(x, y, xi, 'linear'); plot(x, y, 'o', xi, yi, '-'); legend('原始点', '线性插值'); xlabel('x'); ylabel('y'); title('线性插值示例'); grid on;disp('原始点y:'); disp(y); disp('插值后yi:'); disp(yi);
2.拉格朗日插值多项式
首先构造一组基函数:
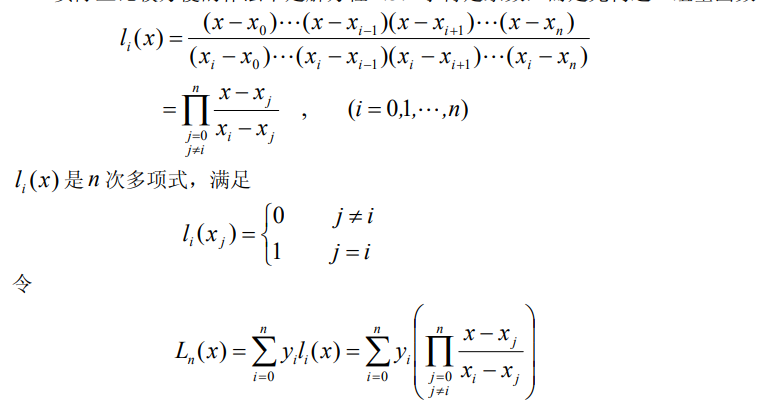
上式称为n 次 Lagrange 插值多项式。
Matlab 中没有现成的 Lagrange 插值函数,必须编写一个 M 文件实现 Lagrange 插值。 设n 个节点数据以数组 x0, y0输入(注意 Matlat 的数组下标从 1 开始),m 个插值 点以数组 x 输入,输出数组 y 为m 个插值。编写一个名为 lagrange.m 的 M 文件:
function y=lagrange(x0,y0,x); n=length(x0);m=length(x); for i=1:m z=x(i); s=0.0; for k=1:n p=1.0; for j=1:n if j~=k p=p*(z-x0(j))/(x0(k)-x0(j)); end end s=p*y0(k)+s; end y(i)=s; end 代入数据:
x0 = [1, 3, 5, 7, 9]; y0 = [2, 4, 6, 8, 10]; x = 1:0.5:9;y=lagrange(x0,y0,x); disp('原始点y0:'); disp(y0); disp('插值后y:'); disp(y);输出结果:

3.牛顿(Newton)插值

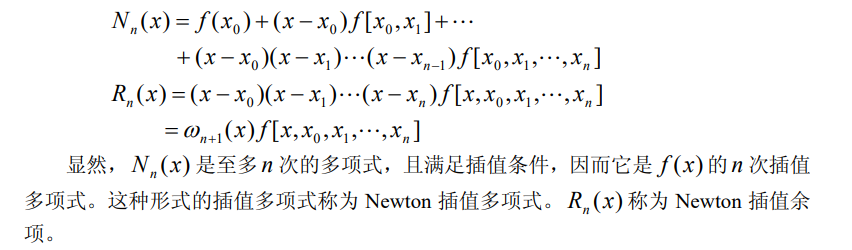
运行程序:
function yi = newtonInterpolation(x, y, xi) n = length(x); % 已知数据点的数量 if n ~= length(y) error('x和y的长度必须相等'); end % 构建差分表 diffTable = zeros(n, n); diffTable(:, 1) = y(:); % 第一列是y值 for j = 2:n for i = 1:n-j+1 diffTable(i, j) = (diffTable(i+1, j-1) - diffTable(i, j-1)) / (x(i+j-1) - x(i)); end end if ~isvector(xi) yi = diffTable(1, 1); % 插值多项式的常数项 for k = 2:n p = 1; for j = 1:k-1 p = p * (xi - x(j)); end yi = yi + diffTable(1, k) * p; end else yi = zeros(size(xi)); for i = 1:length(xi) yi_temp = diffTable(1, 1); % 插值多项式的常数项 for k = 2:n p = 1; for j = 1:k-1 p = p * (xi(i) - x(j)); end yi_temp = yi_temp + diffTable(1, k) * p; end yi(i) = yi_temp; end end end代入数据:
x = [0, 1, 2, 3, 4]; y = [1, 0.8, 0.9, 0.1, -0.8]; xi =0:0.5:5; yi = newtonInterpolation(x, y, xi); % 绘图 plot(x, y, 'o', xi, yi, '-'); legend('原始数据点', '牛顿插值'); xlabel('x'); ylabel('y'); title('牛顿插值示例'); grid on;disp('原始点y:'); disp(y); disp('插值后yi:'); disp(yi);运行结果:
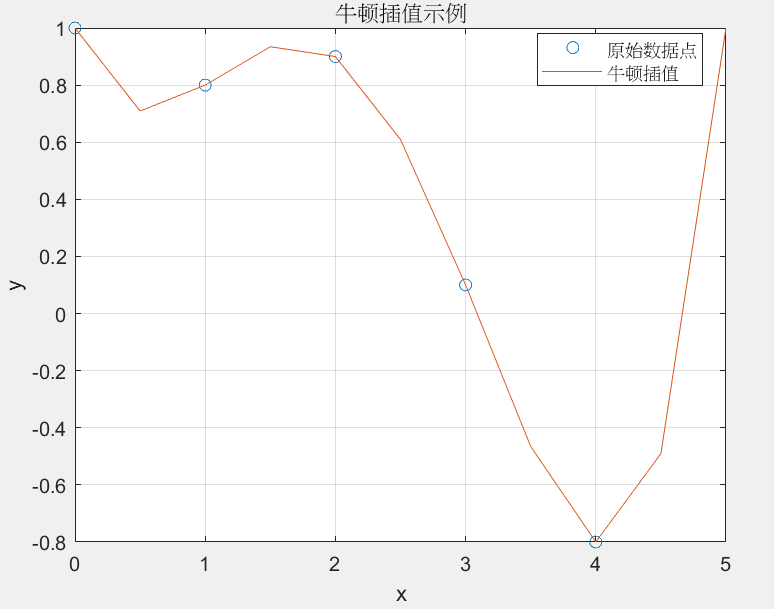
 4.埃尔米特(Hermite)插值
4.埃尔米特(Hermite)插值
如果对插值函数,不仅要求它在节点处与函数同值,而且要求它与函数有相同的一 阶、二阶甚至更高阶的导数值,这就是 Hermite 插值问题。

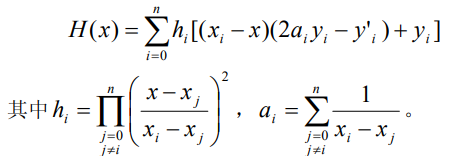
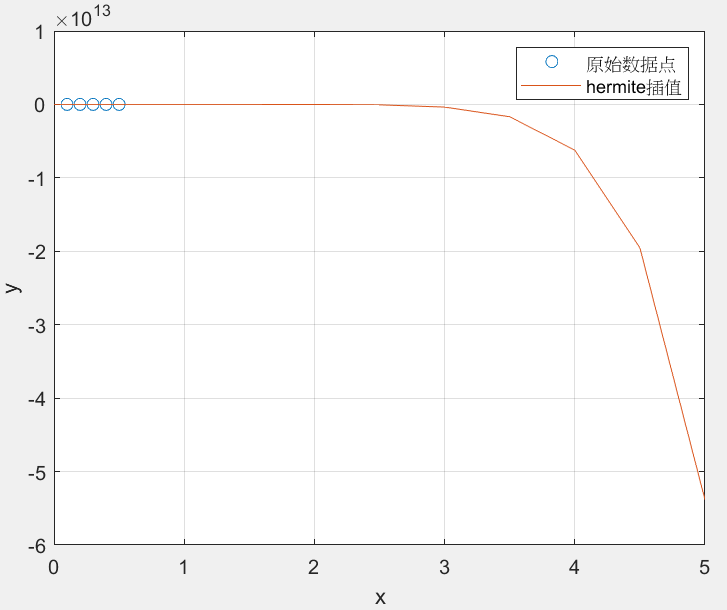
运行程序:
function y=hermite(x0,y0,y1,x); n=length(x0);m=length(x); for k=1:m yy=0.0; for i=1:n h=1.0; a=0.0; for j=1:n if j~=i h=h*((x(k)-x0(j))/(x0(i)-x0(j)))^2; a=1/(x0(i)-x0(j))+a; end end yy=yy+h*((x0(i)-x(k))*(2*a*y0(i)-y1(i))+y0(i)); end y(k)=yy; end 代入数据:
x0=[0.1, 0.2,0.3,0.4,0.5]; y0=[1,2,3,4,5]; y1=[2,4,6,8,10];xi =0:0.5:5; yi = hermite(x0, y0,y1, xi); % 绘图 plot(x0, y0, 'o', xi, yi, '-'); legend('原始数据点', 'hermite插值'); xlabel('x'); ylabel('y'); grid on;disp('原始点y0:'); disp(y0); disp('插值后yi:'); disp(yi);运行结果: