前言:并查集(Union-Find)是一种常用的数据结构,主要用于解决动态连通性问题。它维护了一组不相交的集合,并提供了两种核心操作:合并(Union)和查找(Find),这些操作可以高效地用于解决一系列的图论问题,如连通分量、最小生成树等。

✨✨✨这里是秋刀鱼不做梦的BLOG
✨✨✨想要了解更多内容可以访问我的主页秋刀鱼不做梦-CSDN博客
在开始讲解并查集之前,先让我们看一下本文大致的讲解内容:
目录
1.并查集的简介
2.并查集的自我实现
3.并查集的优化
(1)路径压缩
(2)按秩合并
4.并查集的应用
应用一:图的连通分量
应用二:判断是否存在环
应用三:Kruskal算法求最小生成树
1.并查集的简介
在开始学习使用并查集之前,先让我们了解一下什么是并查集:
——并查集是一种数据结构,用于管理一些不相交的集合。其支持两种主要操作:
查找(Find):确定某个元素属于哪个集合。
合并(Union):将两个不同的集合合并为一个集合。
我们可以从这个数据结构的名字中就可以了解这个数据结构的使用场景,合并两个集合以及查找两个元素是否属于同一个集合。
了解完了并查集的使用场景之后,在让我们看一下并查集底层的原理:
并查集底层是通过数组来实现。数组的下标表示元素,数组的值表示该元素所在集合的父节点,如果一个元素是集合的代表(根节点),则值为负数,负数的绝对值表示集合中元素的数量(可以将并查集的每一个集合看作一棵树,但是其值的存储却是使用数组来进行存储的)。
如图:
最开始的并查集
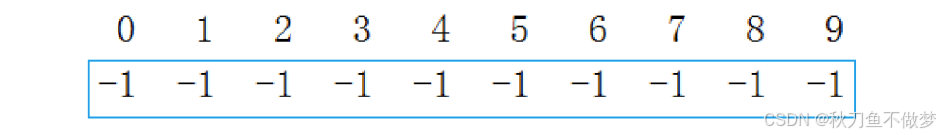
将并查集的元素进行分组(类似于设置树的根节点和分支):
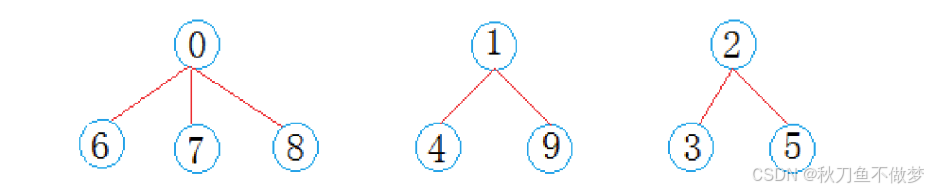
最终的并查集:
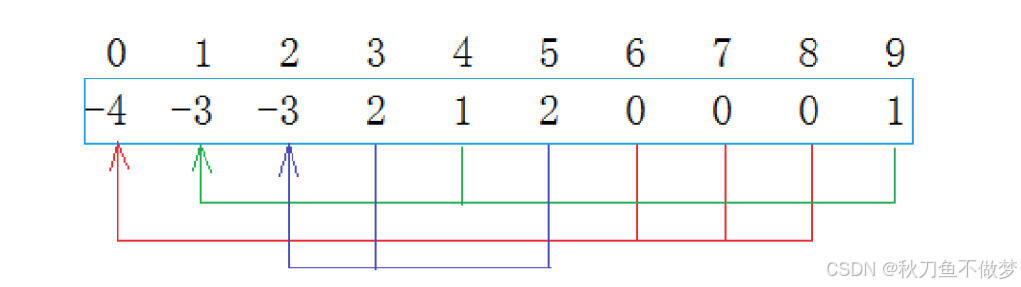
从上图中我们可以了解到:0、1、2为每个集合的根节点,0集合中包含4个元素,1集合中包含3个元素,2集合中包含3个元素,其中每种不同颜色的线连接起来的节点为一个组。
这样我们就大致的了解了并查集的基本原理了。
2.并查集的自我实现
在了解了并查集的基本原理之后,我们就可以自我实现并查集了,以下为自我实现并查集的代码:
import java.util.Arrays;public class UnionFindSet { // 并查集的底层为一个数组 private int[] element; // 构造函数,初始化并查集 public UnionFindSet(int initial) { element = new int[initial]; Arrays.fill(element, -1); // 初始化数组,表示每个元素自成一个集合 } // 查找两个元素是否在同一个集合内 public boolean isSameSet(int val1, int val2) { return findRoot(val1) == findRoot(val2); // 比较两个元素的根节点 } // 查找元素的根节点 private int findRoot(int val) { if (val < 0) { throw new ArrayIndexOutOfBoundsException("索引越界!!!"); // 检查索引是否合法 } // 查找根节点 while (element[val] >= 0) { val = element[val]; // 沿着父节点向上查找 } return val; // 返回根节点 } // 合并两个集合 public void unionSet(int val1, int val2) { int index1 = findRoot(val1); // 找到val1的根节点 int index2 = findRoot(val2); // 找到val2的根节点 if (!(index1 == index2)) { // 如果两个元素不在同一集合 element[index1] = element[index1] + element[index2]; // 更新集合大小 element[index2] = index1; // 将index2的根节点指向index1 } } // 返回当前集合的个数 public int SetNumber() { int count = 0; // 计数器 for (int i = 0; i < element.length; i++) { if (element[i] < 0) { count++; // 每找到一个根节点,计数器加一 } } return count; // 返回集合的个数 }}希望读者可以跟随上述代码中的注释对自我实现并查集进行理解,这里我们在对上述代码进行总结梳理一下:
查找方法
boolean isSameSet(int val1, int val2):判断两个元素是否在同一集合,通过比较它们的根节点实现。
private int findRoot(int val):递归查找元素的根节点,若索引越界则抛出异常。
合并方法
void unionSet(int val1, int val2):合并两个元素所属的集合。若它们的根节点不同,则更新父节点关系,并合并集合的大小。
集合计数
int SetNumber():遍历数组,统计当前集合的个数,通过计数负值(根节点)来实现。
这样我们就自我实现了一个并查集了!!!
3.并查集的优化
从上述对并查集的自我实现中,我们可以发现两个问题:
(1)当我们查找某个节点的时候,当树的高度与集合元素的数量相同,会导致查找操作的时间复杂度最坏情况下为O(n),在这种情况下,每次查找都需要遍历整棵树;
(2)合并两个集合时,如果不考虑树的结构,可能会将较小的树合并到较大的树上,从而导致树的高度增加,从而增加后续操作的时间复杂度;
——为了解决上述的两个问题,我们就需要进行路径压缩和按秩合并
(1)路径压缩
目的:在查找根节点的过程中,通过将查找路径上的所有节点直接连接到根节点,来降低树的高度。
效果:每次查找操作后,树的深度减少,从而使后续的查找操作更加高效。路径压缩将树转变为较扁平的结构,降低了查找的时间复杂度,平均情况下接近O(1)。
了解为什么要进行路径压缩之后,那么我们如何去实现路径压缩呢?以下为实现路径压缩的代码:
// 路径压缩 - 查找根节点 - 使每个节点的值直接为根节点public int findRoot2(int val) { // 检查索引是否越界 if (val < 0 || val >= element.length) { throw new ArrayIndexOutOfBoundsException("索引越界!!!"); } // 如果当前元素是根节点,直接返回 if (element[val] < 0) { return val; } else { // 递归查找根节点,并在此过程中进行路径压缩 element[val] = findRoot2(element[val]); // 将当前节点的父节点直接指向根节点 return element[val]; // 返回根节点 }}注释说明:
方法首先检查传入的索引val是否在合法范围内。
如果val是根节点(即数组值为负数),则直接返回该节点。
否则,递归查找其父节点,并将当前节点直接连接到找到的根节点,实现路径压缩,最终返回根节点。
——这样我们就了解了如何去进行路劲压缩了。
(2)按秩合并
目的:在合并两个集合时,始终将较小的树合并到较大的树上,以保持树的平衡。
效果:通过控制树的高度,避免形成过于深的结构,从而进一步降低查找操作的时间复杂度。按秩合并使得树的高度保持在一个较小的范围内,通常不超过O(log n)。
了解为什么要进行按秩合并之后,那么我们如何去实现按秩合并呢?以下为实现路径压缩的代码:
// 按秩合并 - 合并两个集合,将树高度低的接在树高度高的上public void unionSet2(int val1, int val2) { // 找到val1和val2的根节点 int index1 = findRoot(val1); int index2 = findRoot(val2); // 如果两个元素的根节点不同,进行合并 if (index1 != index2) { // 判断树的高度(通过数组中的值判断)进行合并 if (element[index1] < element[index2]) { // 将index1的集合合并到index2的集合上 element[index1] += element[index2]; // 更新index1集合的大小 element[index2] = index1; // 将index2的根指向index1 } else { // 将index2的集合合并到index1的集合上 element[index2] += element[index1]; // 更新index2集合的大小 element[index1] = index2; // 将index1的根指向index2 } }}注释说明:
方法首先找到两个元素val1和val2的根节点。
如果两个根节点不同,说明它们属于不同的集合,接着进行合并操作。
通过比较两个根节点对应的数组值(表示集合大小)来判断树的高度,将较低的树合并到较高的树上,从而保持树的平衡。
这样我们就大致的了解了如何去对并查集进行路径压缩和按秩合并优化了。
4.并查集的应用
了解完了并查集的基本使用之后,在让我们看看并查集的应用场景,并查集在解决动态连通性问题时非常高效,尤其在处理以下问题时有显著的表现:
连通分量:判断图中的连通性。
最小生成树:Kruskal算法的实现。
动态连接问题:快速判断两点是否在同一个集合中。
应用一:图的连通分量
一个常见的应用场景是计算图中的连通分量。我们可以将每个节点看作一个独立的集合,使用union操作来合并连通的节点,最后统计连通分量的数量。
// 计算图中的连通分量数量public int countComponents(int n, int[][] edges) { // 初始化并查集,包含n个节点 UnionFind uf = new UnionFind(n); // 遍历每条边,将连接的节点合并到同一个集合 for (int[] edge : edges) { uf.union(edge[0], edge[1]); } int components = 0; // 计数器,用于统计连通分量的数量 // 遍历每个节点,查找根节点 for (int i = 0; i < n; i++) { // 如果当前节点是根节点,说明找到一个新的连通分量 if (uf.find(i) == i) { components++; // 计数器加一 } } // 返回连通分量的数量 return components;}应用二:判断是否存在环
在无向图中,我们可以使用并查集来判断图中是否存在环。当我们遍历图中的每一条边时,如果该边的两个顶点已经属于同一个集合,则说明该边形成了一个环。
// 检查图中是否存在环public boolean hasCycle(int n, int[][] edges) { // 初始化并查集,包含n个节点 UnionFind uf = new UnionFind(n); // 遍历每条边 for (int[] edge : edges) { // 检查当前边的两个节点是否已经连接 if (uf.isConnected(edge[0], edge[1])) { return true; // 如果已连接,说明存在环 } // 如果未连接,则合并这两个节点 uf.union(edge[0], edge[1]); } // 遍历完所有边后,未发现环 return false;}应用三:Kruskal算法求最小生成树
Kruskal算法是求解最小生成树的一种常用方法。该算法的核心思想是:每次选择权重最小的边,若该边不会形成环,则将其加入生成树中,直到树中包含所有节点为止。
class Edge { int u, v, weight; // 边的两个端点和权重 // 构造函数,初始化边的端点和权重 public Edge(int u, int v, int weight) { this.u = u; // 端点u this.v = v; // 端点v this.weight = weight; // 边的权重 }}public int kruskal(int n, List<Edge> edges) { // 按边的权重进行排序 edges.sort((a, b) -> a.weight - b.weight); // 初始化并查集,包含n个节点 UnionFind uf = new UnionFind(n); int mstWeight = 0; // 最小生成树的总权重 int edgeCount = 0; // 已加入最小生成树的边的数量 // 遍历所有边 for (Edge edge : edges) { // 如果这条边的两个端点不在同一集合中 if (!uf.isConnected(edge.u, edge.v)) { uf.union(edge.u, edge.v); // 合并集合 mstWeight += edge.weight; // 加入当前边的权重 edgeCount++; // 已加入的边数加一 // 如果已经加入n-1条边,停止遍历 if (edgeCount == n - 1) { break; } } } // 返回最小生成树的总权重 return mstWeight;}至此,通过上述的简单介绍之后,我们就可以了解并查集的应用了!
以上就是本篇文章的全部内容了~~~