你在泰坦尼克号上你能活下来吗?
泰坦尼克号的沉没是历史上最具影响力的海难之一,在1912年4月15日,泰坦尼克号的处女航中,与冰山相撞后沉没。在当时,船上没有足够的救生艇供所有人使用,导致2224名乘客和机组人员中的1502人死亡。虽然幸存有一些运气成分,但似乎有些人比其他人更有可能生存。
泰坦尼克号预测项目从kaggle建站开始,已经经历了很多大佬的分析建模,有2万多的团队参与过该项目,是你加入kaggle最好的项目之一。
- 数据来源:https://www.kaggle.com/c/titanic/overview
- 本文主要是根据解决《泰坦尼克号》竞赛和Manav Sehgal分享和一些其他来源的出色分享创建的,主要目的是为了对机器学习的各位提供一些项目实践,原文地址如下:
- https://www.kaggle.com/startupsci/titanic-data-science-solutions
- A journey through Titanic
- Getting Started with Pandas: Kaggle’s Titanic Competition
- Titanic Best Working Classifier
先想明白我们怎么去做
参考《数据科学解决方案》一书,建模的7个流程:
- 定义问题,确定问题知道我们要做什么
- 获取数据,一般是指训练和测试数据。
- 数据清洗,得到一份干净好用的数据
- 数据分析,探索数据,为后续建模做准备。
- 建模,预测和解决问题。
- 可视化报告,呈现问题的解决步骤和最终解决方案。
- 得到结果。
建模流程
确定问题
每个数据集提出的同时也会伴随着问题,kaggle会给与数据说明(https://www.kaggle.com/c/titanic/overview/description ),我们的问题很简单: “什么样的人更有可能生存呢?”
在泰坦尼克竞赛中,我们可以访问两个类似的数据集,训练集和测试集,字段包括乘客信息,例如姓名、年龄、性别、社会经济舱等。训练集为“ train.csv”,测试集为“ test.csv”。Train.csv将包含一部分乘客的详细信息(准确地说是891位乘客),并且重要的是,它会告诉我们他们是否幸存下来。“ test.csv”数据集包含类似的信息,但没有透露每位乘客的是否存活,我们的工作就是利用train.csv的数据训练出模型,去预测机上其他418名乘客(在test.csv中找到)是否幸免于难。
获取数据
kaggle 提供了很方便的下载方式,可以在数据界面中找到并下载数据:https://www.kaggle.com/c/titanic/overview/description
导包
# 导入数据分析一些常用库
import pandas as pd
import numpy as np
import random as rnd
# pd.options.display.max_columns = None
# 可视化包
import seaborn as sns
import matplotlib.pyplot as plt
plt.style.use("seaborn")
%matplotlib inline
sns.set(font="simhei")
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置加载的字体名
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
# 机器学习包
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.tree import DecisionTreeClassifier
导入数据
train_df = pd.read_csv('train.csv')
test_df = pd.read_csv('test.csv')
combine = [train_df, test_df]
预览数据
# 看一下我们有那些字段
print(train_df.columns.values)
['PassengerId' 'Survived' 'Pclass' 'Name' 'Sex' 'Age' 'SibSp' 'Parch'
'Ticket' 'Fare' 'Cabin' 'Embarked']
# 简单看一下我们的数据
train_df.head(3)
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
train_df.tail(3)
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 888 | 889 | 0 | 3 | Johnston, Miss. Catherine Helen "Carrie" | female | NaN | 1 | 2 | W./C. 6607 | 23.45 | NaN | S |
| 889 | 890 | 1 | 1 | Behr, Mr. Karl Howell | male | 26.0 | 0 | 0 | 111369 | 30.00 | C148 | C |
| 890 | 891 | 0 | 3 | Dooley, Mr. Patrick | male | 32.0 | 0 | 0 | 370376 | 7.75 | NaN | Q |
数据清洗
字段整理
- PassengerId 用户编号:目前作为用户唯一标识,此处无特别意义(有些编号是具有价值的,比如身份证)
- Survived 是否幸存:目标字段,是我们要预测的数据
- Pclass 用户阶级:分类字段,1为最高级,3为最低级
- Name 姓名:可以看出家族关系
- Sex 性别
- Age 年龄
- SibSp:泰坦尼克号上与乘客同行的兄弟姐妹(Siblings)和配偶(Spouse)数目
- Parch:描述了泰坦尼克号上与乘客同行的家长(Parents)和孩子(Children)数目
- Ticket 船票号
- Fare 票价
- Cabin 船舱号
- Embarked 乘客上船时的港口
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-L2En3s3d-1614530159408)(attachment:image.png)]
识别特征类型
特征主要类型有:时间型、数值型、类别型、文本型
哪些特征是分类型特征?
类别型特征将相似属性归为一类,但是大多数模型都不能直接处理文本型数据,必须要转换为数值型才能使用。
类别型特征可以分为定类变量、定序变量、定距变量和定比变量。
- 定类变量:如性别(男、女、其他),三种取值之间是相互独立的,彼此之间完全没有关系,这种变量称之为名义变量。
- 定序变量:如学历(小学、初中、高中),三种取值不是完全独立的,我们可以明显看出,在性质上可以有高中>初中>小学这样 的联系,学历有高低,但是学历的取值之间却不是可以计算的,我们不能说小学 + 某个取值 = 初中。这是有序变 量。
- 定距变量:如温度(>25摄氏度、>30摄氏度 、>35摄氏度),各个取值之间有联系,且是可以互相计算的,而且两者的差值有 意义。比如35摄氏度 - 25摄氏度 = 10摄氏度,分类之间可以通过数学计算互相转换。这是有距变量。
- 定比变量:如质量(>10kg、>50kg、>100kg),各个取值之间有联系,不仅可以计算差值,还可以计算其商值。
定序变量:Pclass 用户阶级:分类字段,1为最高级,3为最低级
定类变量:Sex 性别,Embarked 乘客上船时的港口,Survived 是否幸存
哪些特征是数值型特征?
数值型随样本的不同而进行变化,一般分为连续型,离散型,经常使用归一化,离散化等方法进行处理
连续型:Age 年龄,fare 票价。
离散型:SibSp,Parch。
哪些特征是文本型特征?
文本型:Name,姓名中有很多符号,也存在一些错别字的问题
还有一些混合型特征
混合型数据特征:Ticket 船票号,Cabin 船舱号
- 还有1个特征: PassengerId 用户编号(无意义,后续会删除)
数据清洗
空值,数据类型
空值:
训练数据集空值排序:Cabin > Age > Embarked。
测试数据集空值排序:Cabin > Age 。
各特征的数据类型是什么?
训练集:7个特征是整数或浮点数,字符串对象5个。
测试集:6个特征是整数或浮点数,字符串对象5个。
print(train_df.info())
print("--"*20)
print(test_df.info())
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 PassengerId 891 non-null int64
1 Survived 891 non-null int64
2 Pclass 891 non-null int64
3 Name 891 non-null object
4 Sex 891 non-null object
5 Age 714 non-null float64
6 SibSp 891 non-null int64
7 Parch 891 non-null int64
8 Ticket 891 non-null object
9 Fare 891 non-null float64
10 Cabin 204 non-null object
11 Embarked 889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.7+ KB
None
----------------------------------------
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 418 entries, 0 to 417
Data columns (total 11 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 PassengerId 418 non-null int64
1 Pclass 418 non-null int64
2 Name 418 non-null object
3 Sex 418 non-null object
4 Age 332 non-null float64
5 SibSp 418 non-null int64
6 Parch 418 non-null int64
7 Ticket 418 non-null object
8 Fare 417 non-null float64
9 Cabin 91 non-null object
10 Embarked 418 non-null object
dtypes: float64(2), int64(4), object(5)
memory usage: 36.0+ KB
None
- 通过训练集各个特征的分布情况,我们可以得到一些很有用的信息:
- 训练集中有891条数据,泰塔尼克号实际有2224个客户,占旅客实际数量的40%
- 是否幸存是只有0或1的分类特征
- 约有38%的样本存活下来,但泰坦尼克号实际存活率为32%
- 大多数乘客(> 75%)没有和父母或孩子一起旅行
- 近30%的乘客有兄弟姐妹和/或配偶
- 票价差异很大,只有极少的乘客(<1%)支付的费用高达512美元
- 65-80岁年龄段的老年乘客很少(<1%)。
下面会有具体的数据展示
数值型分布
train_df.describe()
| PassengerId | Survived | Pclass | Age | SibSp | Parch | Fare | |
|---|---|---|---|---|---|---|---|
| count | 891.000000 | 891.000000 | 891.000000 | 714.000000 | 891.000000 | 891.000000 | 891.000000 |
| mean | 446.000000 | 0.383838 | 2.308642 | 29.699118 | 0.523008 | 0.381594 | 32.204208 |
| std | 257.353842 | 0.486592 | 0.836071 | 14.526497 | 1.102743 | 0.806057 | 49.693429 |
| min | 1.000000 | 0.000000 | 1.000000 | 0.420000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 223.500000 | 0.000000 | 2.000000 | 20.125000 | 0.000000 | 0.000000 | 7.910400 |
| 50% | 446.000000 | 0.000000 | 3.000000 | 28.000000 | 0.000000 | 0.000000 | 14.454200 |
| 75% | 668.500000 | 1.000000 | 3.000000 | 38.000000 | 1.000000 | 0.000000 | 31.000000 |
| max | 891.000000 | 1.000000 | 3.000000 | 80.000000 | 8.000000 | 6.000000 | 512.329200 |
类别型特征的分布
姓名在数据集中是唯一的(count = unique = 891)
性别变量有2个值,其中男性占65%(top=男性,freq = 577 / count = 891)。
船舱号在样本中具有多个重复项。也可以看出,有几个乘客共用一个船舱。
港口有3个可能的值。大多数乘客使用的S端口(top= S)
船票号具有很高的重复率(unique = 681),为22%。
# 类别型分布
train_df.describe(include=['O'])
| Name | Sex | Ticket | Cabin | Embarked | |
|---|---|---|---|---|---|
| count | 891 | 891 | 891 | 204 | 889 |
| unique | 891 | 2 | 681 | 147 | 3 |
| top | Slabenoff, Mr. Petco | male | 1601 | G6 | S |
| freq | 1 | 577 | 7 | 4 | 644 |
数据探索及猜想
数据分析猜想
基于到目前为止完成的数据分析,我们得出以下假设,在采取适当措施之前,我们可能会进一步验证这些假设。
1. Correlating.相关性
我们想知道每个特征与生存率的关联程度。找到他们的相关关系,尽可能在早期就去做它,并将相关性与项目后期的建模相关性进行匹配。
2. Completing.完成
我们可能要完成“年龄”特征,因为它肯定与生存相关。
我们可能要完成“港口”特征,因为它也可能与生存或其他重要功能相关。
3. Correcting.纠正
船票号特征可能会从我们的分析中删除,因为它包含很高的重复率(22%),并且船票号与生存率之间可能没有关联。
船舱号特征可能由于高度不完整或在训练和测试数据集中包含许多空值而被删除。
游客ID可能会从训练数据集中删除,因为它对生存没有帮助,没什么意义。
姓名特征是相对非标准的,可能不会直接有助于生存分析,因此可能会被放弃。
4. Creating.创建
我们可能想基于Parch和SibSp创建一个称为“家庭”的新特征,以获取船上家庭成员的总数。
我们可能要设计名称特征,以将姓提取为新特征。
我们可能要为年龄段创建新功能。这会将连续的数字特征转换为序数分类特征。
如果它有助于我们的分析,我们可能还想创建一个票价范围特征。
5. Classifying.分类
我们也可以根据前面提到的问题描述增加假设。
女性(性别=女性)更有可能存活下来。
儿童(年龄<?)存活的可能性更高。
上等乘客(Pclass = 1)更有可能幸存下来。
透视表分析
透视表分析,类似Excel中的数据透视表,可以看到数据的分布趋势
为了确认我们的一些观察和假设,我们可以通过使特征独立来快速分析特征的相关性。在此阶段,我们只能对没有任何空值的特征执行此操作。对分类型(Sex),有序型(Pclass)或离散型的(SibSp,Parch)的特征这样做也是有意义的。
1. Pclass我们发现Pclass = 1和Survived之间存在显着相关性(> 0.5)。我们决定在模型中包括此功能。
2. 性别,我们观察问题可以发现,即性别=女性具有很高的生存率,为74%。
3. SibSp和Parch这些特征对于某些值零相关。最好是从这些单个特征中派生一个特征或一组特征,做一个更好的特征出来。
# 上等乘客更容易存活
train_df[['Pclass', 'Survived'
]].groupby(['Pclass'],
as_index=False).mean().sort_values(by='Survived',
ascending=False)
| Pclass | Survived | |
|---|---|---|
| 0 | 1 | 0.629630 |
| 1 | 2 | 0.472826 |
| 2 | 3 | 0.242363 |
# 女性更容易存活
train_df[['Sex', 'Survived']].groupby(['Sex'],as_index=False).mean().sort_values(by='Survived',
ascending=False)
| Sex | Survived | |
|---|---|---|
| 0 | female | 0.742038 |
| 1 | male | 0.188908 |
# 与乘客同行的兄弟姐妹和配偶数量
train_df[["SibSp", "Survived"
]].groupby(['SibSp'],
as_index=False).mean().sort_values(by='Survived',
ascending=False)
| SibSp | Survived | |
|---|---|---|
| 1 | 1 | 0.535885 |
| 2 | 2 | 0.464286 |
| 0 | 0 | 0.345395 |
| 3 | 3 | 0.250000 |
| 4 | 4 | 0.166667 |
| 5 | 5 | 0.000000 |
| 6 | 8 | 0.000000 |
# 与乘客同行的家长和孩子的数目
train_df[["Parch", "Survived"
]].groupby(['Parch'],
as_index=False).mean().sort_values(by='Survived',
ascending=False)
| Parch | Survived | |
|---|---|---|
| 3 | 3 | 0.600000 |
| 1 | 1 | 0.550847 |
| 2 | 2 | 0.500000 |
| 0 | 0 | 0.343658 |
| 5 | 5 | 0.200000 |
| 4 | 4 | 0.000000 |
| 6 | 6 | 0.000000 |
可视化分析
可视化分析,通过图表来形象的刻画数据,确认一些假设,为后续建模做准备
1. 关联数字特征
首先要了解数值特征与我们的求解目标之间的相关性。
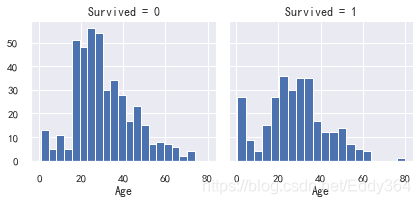
一般使用直方图分析连续数字变量(例如Age),直方图可以使用自动定义的bin或等距范围的带指示样本的分布。这有助于我们回答与特定频段有关的问题(比如:婴儿的存活率更高吗?)
2. 观察可视化
婴儿(年龄<= 4)具有较高的存活率。
年龄最大的乘客(年龄= 80)幸存下来。
15至25岁的大批人无法生存。
大多数乘客年龄在15-35岁之间。
3. 决定
通过简单的可视化分析证实了我们的假设,为后面的建模做铺垫。
在模型训练中要考虑年龄。
补充年龄特征(空值)。
分组年龄。
g = sns.FacetGrid(train_df, col='Survived')
g.map(plt.hist, 'Age', bins=20)
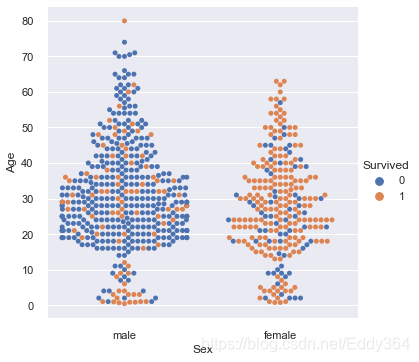
sns.set()
sns.catplot(data=train_df, kind="swarm", x="Sex",y="Age", hue="Survived")
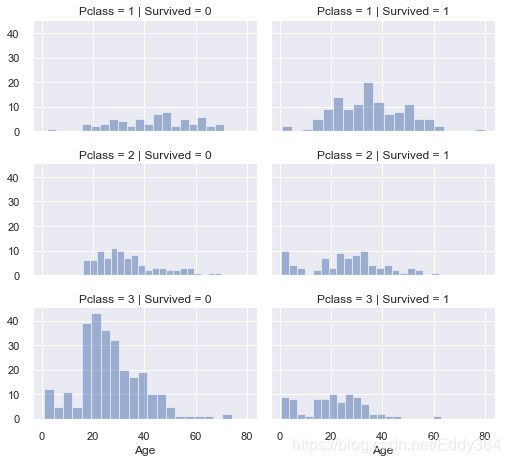
# grid = sns.FacetGrid(train_df, col='Pclass', hue='Survived')
grid = sns.FacetGrid(train_df, col='Survived', row='Pclass', size=2.2, aspect=1.6)
grid.map(plt.hist, 'Age', alpha=.5, bins=20)
grid.add_legend();
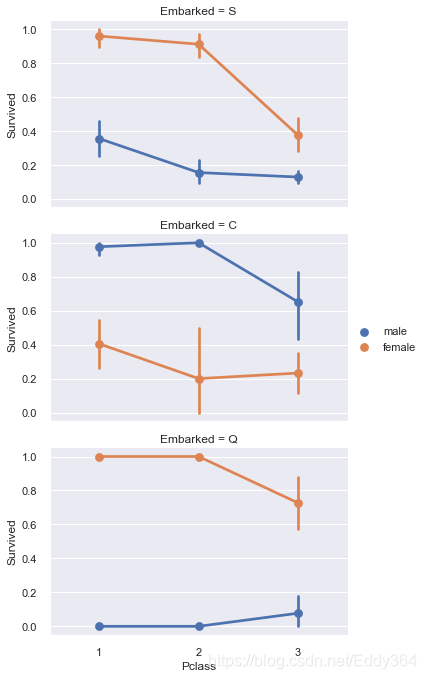
# grid = sns.FacetGrid(train_df, col='Embarked')
grid = sns.FacetGrid(train_df, row='Embarked', size=3.2, aspect=1.6)
grid.map(sns.pointplot, 'Pclass', 'Survived', 'Sex', palette='deep')
grid.add_legend()
make数据
数据分析猜想
基于到目前为止完成的数据分析,我们已经得到了许多有用的信息,现在我们要利用之前得到的信息对我们的数据,进行选择,纠正,创造,选择我们需要的数据,化繁为简,以点透面。
删除特征
通过删除特性,我们可以处理更少的数据,加速数据处理,简化分析。
基于前面我们的分析和假设:
- 删除Cabin(船舱号),它的缺失率很高(只有204条数据),空值太多且对于是否生存来说可能没啥效果
- 删除Ticket(船票号),因为它包含很高的重复率(22%),并且船票号与生存率之间可能没有关联
通常我们可以同时对训练和测试数据集删除无意义的字段。
print("Before", train_df.shape, test_df.shape, combine[0].shape, combine[1].shape)
train_df = train_df.drop(['Ticket', 'Cabin'], axis=1)
test_df = test_df.drop(['Ticket', 'Cabin'], axis=1)
combine = [train_df, test_df]
"After", train_df.shape, test_df.shape, combine[0].shape, combine[1].shape
Before (891, 12) (418, 11) (891, 12) (418, 11)
('After', (891, 10), (418, 9), (891, 10), (418, 9))
从现有特征中提取新特征,创造一个合适新特征可以让模型更加准确。
在去掉名字和乘客id特征之前,我们想分析一下是否可以通过名字这个特征来提取到一些有用的信息,仔细去看姓名这个特征会发现在姓前面是有记载着一些头衔的,Miss,Mr,Sir等等,这些会不会和生存有关系呢,提取出这些称呼看一下:
观察数据
某些头衔大多活了下来(夫人、女士、先生)
我们决定保留新的title特征用于模型训练。
#使用正则表达式提取标题
for dataset in combine:
dataset['Title'] = dataset.Name.str.extract(' ([A-Za-z]+)\.', expand=False)
pd.crosstab(train_df['Title'], train_df['Sex'])
| Sex | female | male |
|---|---|---|
| Title | ||
| Capt | 0 | 1 |
| Col | 0 | 2 |
| Countess | 1 | 0 |
| Don | 0 | 1 |
| Dr | 1 | 6 |
| Jonkheer | 0 | 1 |
| Lady | 1 | 0 |
| Major | 0 | 2 |
| Master | 0 | 40 |
| Miss | 182 | 0 |
| Mlle | 2 | 0 |
| Mme | 1 | 0 |
| Mr | 0 | 517 |
| Mrs | 125 | 0 |
| Ms | 1 | 0 |
| Rev | 0 | 6 |
| Sir | 0 | 1 |
for dataset in combine:
dataset['Title'] = dataset['Title'].replace([
'Lady', 'Countess', 'Capt', 'Col', 'Don', 'Dr', 'Major', 'Rev', 'Sir',
'Jonkheer', 'Dona'
], 'Rare')
dataset['Title'] = dataset['Title'].replace('Mlle', 'Miss')
dataset['Title'] = dataset['Title'].replace('Ms', 'Miss')
dataset['Title'] = dataset['Title'].replace('Mme', 'Mrs')
train_df[['Title', 'Survived']].groupby(['Title'], as_index=False).mean()
| Title | Survived | |
|---|---|---|
| 0 | Master | 0.575000 |
| 1 | Miss | 0.702703 |
| 2 | Mr | 0.156673 |
| 3 | Mrs | 0.793651 |
| 4 | Rare | 0.347826 |
dataset
| PassengerId | Pclass | Name | Sex | Age | SibSp | Parch | Fare | Embarked | Title | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 892 | 3 | Kelly, Mr. James | male | 34.5 | 0 | 0 | 7.8292 | Q | Mr |
| 1 | 893 | 3 | Wilkes, Mrs. James (Ellen Needs) | female | 47.0 | 1 | 0 | 7.0000 | S | Mrs |
| 2 | 894 | 2 | Myles, Mr. Thomas Francis | male | 62.0 | 0 | 0 | 9.6875 | Q | Mr |
| 3 | 895 | 3 | Wirz, Mr. Albert | male | 27.0 | 0 | 0 | 8.6625 | S | Mr |
| 4 | 896 | 3 | Hirvonen, Mrs. Alexander (Helga E Lindqvist) | female | 22.0 | 1 | 1 | 12.2875 | S | Mrs |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 413 | 1305 | 3 | Spector, Mr. Woolf | male | NaN | 0 | 0 | 8.0500 | S | Mr |
| 414 | 1306 | 1 | Oliva y Ocana, Dona. Fermina | female | 39.0 | 0 | 0 | 108.9000 | C | Rare |
| 415 | 1307 | 3 | Saether, Mr. Simon Sivertsen | male | 38.5 | 0 | 0 | 7.2500 | S | Mr |
| 416 | 1308 | 3 | Ware, Mr. Frederick | male | NaN | 0 | 0 | 8.0500 | S | Mr |
| 417 | 1309 | 3 | Peter, Master. Michael J | male | NaN | 1 | 1 | 22.3583 | C | Master |
418 rows × 10 columns
#将分类特征转换成数值型
title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Rare": 5}
for dataset in combine:
dataset['Title'] = dataset['Title'].map(title_mapping)
dataset['Title'] = dataset['Title'].fillna(0)
train_df.head()
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Fare | Embarked | Title | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | 7.2500 | S | 1 |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | 71.2833 | C | 3 |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | 7.9250 | S | 2 |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 53.1000 | S | 3 |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 8.0500 | S | 1 |
#现在把姓名和PassengerId删除
print("Before", train_df.shape, test_df.shape, combine[0].shape, combine[1].shape)
train_df = train_df.drop(['Name', 'PassengerId'], axis=1)
test_df = test_df.drop(['Name', 'PassengerId'], axis=1)
combine = [train_df, test_df]
"After", train_df.shape, test_df.shape, combine[0].shape, combine[1].shape
Before (891, 11) (418, 10) (891, 11) (418, 10)
('After', (891, 9), (418, 8), (891, 9), (418, 8))
转换分类特性
大部分的模型都不能直接处理文本数据,需要将分类型数据转换成数值型,目前我们还有Sex性别变量需要进行转换
for dataset in combine:
dataset['Sex'] = dataset['Sex'].map( {'female': 1, 'male': 0} ).astype(int)
train_df.head()
| Survived | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | Title | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 0 | 22.0 | 1 | 0 | 7.2500 | S | 1 |
| 1 | 1 | 1 | 1 | 38.0 | 1 | 0 | 71.2833 | C | 3 |
| 2 | 1 | 3 | 1 | 26.0 | 0 | 0 | 7.9250 | S | 2 |
| 3 | 1 | 1 | 1 | 35.0 | 1 | 0 | 53.1000 | S | 3 |
| 4 | 0 | 3 | 0 | 35.0 | 0 | 0 | 8.0500 | S | 1 |
现在我们已经得到了一份看起来很不错的数据,有我们需要的字段,但一些字段仍有很多的空值,会影响模型的准确度,接下来我们要使用一些方法进行空值填充,缺失值填充有许多方法,一般的有,特殊值填充,均值/众数/中位数填充,人工补充(利用数据间的联系进行补充或者重新采集等),机器学习方法填充等(回归,最大似然估计、聚类等)。值得一说的是实际情况如果对模型的精度的要求不高或者特征的作用有限的情况下,考虑到运行效率的问题可以删除一些缺失度较高的特征。
补充连续数值型特征
现在,我们应该开始评估和填充缺失值或空值,我们对于目前模型来说可以考虑三种方法来完成数值连续特征。
- 一个简单的方法是在均值和标准偏差之间生成随机数。
- 更准确的猜测缺失值的方法是使用其他相关特征。在我们的案例中,我们注意到年龄、性别和Pclass之间的相关性。我们可以使用Pclass和性别特征组合的年龄中位数猜测年龄值。因此,Pclass=1, Gender=0, Pclass=1, Gender=1,依此类推…
- 结合方法1和2。因此,不要根据中位数猜测年龄值,而是根据Pclass和性别组合,在平均值和标准偏差之间使用随机数字。方法1和3将在我们的模型中引入随机噪声。多次执行的结果可能不同。我们更喜欢方法二。
# grid = sns.FacetGrid(train_df, col='Pclass', hue='Gender')
grid = sns.FacetGrid(train_df, row='Pclass', col='Sex', size=2.2, aspect=1.6)
grid.map(plt.hist, 'Age', alpha=.5, bins=20)
grid.add_legend()
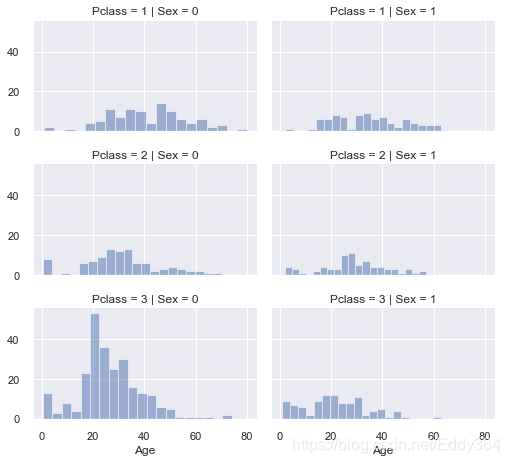
#现在开始用性别和Pclass 预测年龄,用数组储存
guess_ages = np.zeros((2,3))
guess_ages
array([[0., 0., 0.],
[0., 0., 0.]])
#遍历 Sex和Pclass 进行预测
for dataset in combine:
for i in range(0, 2):
for j in range(0, 3):
guess_df = dataset[(dataset['Sex'] == i)
& (dataset['Pclass'] == j + 1)]['Age'].dropna()
# age_mean = guess_df.mean()
# age_std = guess_df.std()
# age_guess = rnd.uniform(age_mean - age_std, age_mean + age_std)
age_guess = guess_df.median()
guess_ages[i, j] = int(age_guess / 0.5 + 0.5) * 0.5
for i in range(0, 2):
for j in range(0, 3):
dataset.loc[(dataset.Age.isnull()) & (dataset.Sex == i) &
(dataset.Pclass == j + 1), 'Age'] = guess_ages[i, j]
dataset['Age'] = dataset['Age'].astype(int)
train_df.head()
| Survived | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | Title | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 0 | 22 | 1 | 0 | 7.2500 | S | 1 |
| 1 | 1 | 1 | 1 | 38 | 1 | 0 | 71.2833 | C | 3 |
| 2 | 1 | 3 | 1 | 26 | 0 | 0 | 7.9250 | S | 2 |
| 3 | 1 | 1 | 1 | 35 | 1 | 0 | 53.1000 | S | 3 |
| 4 | 0 | 3 | 0 | 35 | 0 | 0 | 8.0500 | S | 1 |
#切分年龄,将年龄分段看看和存活之间的关系
train_df['AgeBand'] = pd.cut(train_df['Age'], 5)
train_df[['AgeBand', 'Survived'
]].groupby(['AgeBand'],
as_index=False).mean().sort_values(by='AgeBand',
ascending=True)
| AgeBand | Survived | |
|---|---|---|
| 0 | (-0.08, 16.0] | 0.550000 |
| 1 | (16.0, 32.0] | 0.337374 |
| 2 | (32.0, 48.0] | 0.412037 |
| 3 | (48.0, 64.0] | 0.434783 |
| 4 | (64.0, 80.0] | 0.090909 |
for dataset in combine:
dataset.loc[ dataset['Age'] <= 16, 'Age'] = 0
dataset.loc[(dataset['Age'] > 16) & (dataset['Age'] <= 32), 'Age'] = 1
dataset.loc[(dataset['Age'] > 32) & (dataset['Age'] <= 48), 'Age'] = 2
dataset.loc[(dataset['Age'] > 48) & (dataset['Age'] <= 64), 'Age'] = 3
dataset.loc[ dataset['Age'] > 64, 'Age']
train_df.head()
| Survived | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | Title | AgeBand | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 0 | 1 | 1 | 0 | 7.2500 | S | 1 | (16.0, 32.0] |
| 1 | 1 | 1 | 1 | 2 | 1 | 0 | 71.2833 | C | 3 | (32.0, 48.0] |
| 2 | 1 | 3 | 1 | 1 | 0 | 0 | 7.9250 | S | 2 | (16.0, 32.0] |
| 3 | 1 | 1 | 1 | 2 | 1 | 0 | 53.1000 | S | 3 | (32.0, 48.0] |
| 4 | 0 | 3 | 0 | 2 | 0 | 0 | 8.0500 | S | 1 | (32.0, 48.0] |
#这样年龄段就做好了
train_df = train_df.drop(['AgeBand'], axis=1)
combine = [train_df, test_df]
train_df.head()
| Survived | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | Title | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 0 | 1 | 1 | 0 | 7.2500 | S | 1 |
| 1 | 1 | 1 | 1 | 2 | 1 | 0 | 71.2833 | C | 3 |
| 2 | 1 | 3 | 1 | 1 | 0 | 0 | 7.9250 | S | 2 |
| 3 | 1 | 1 | 1 | 2 | 1 | 0 | 53.1000 | S | 3 |
| 4 | 0 | 3 | 0 | 2 | 0 | 0 | 8.0500 | S | 1 |
继续精简数据,利用SibSp和Parch创建一个新特征
#FamilySize
for dataset in combine:
dataset['FamilySize'] = dataset['SibSp'] + dataset['Parch'] + 1
train_df[['FamilySize', 'Survived'
]].groupby(['FamilySize'],
as_index=False).mean().sort_values(by='Survived',
ascending=False)
| FamilySize | Survived | |
|---|---|---|
| 3 | 4 | 0.724138 |
| 2 | 3 | 0.578431 |
| 1 | 2 | 0.552795 |
| 6 | 7 | 0.333333 |
| 0 | 1 | 0.303538 |
| 4 | 5 | 0.200000 |
| 5 | 6 | 0.136364 |
| 7 | 8 | 0.000000 |
| 8 | 11 | 0.000000 |
#IsAlone 单独一人来的
for dataset in combine:
dataset['IsAlone'] = 0
dataset.loc[dataset['FamilySize'] == 1, 'IsAlone'] = 1
train_df[['IsAlone', 'Survived']].groupby(['IsAlone'], as_index=False).mean()
| IsAlone | Survived | |
|---|---|---|
| 0 | 0 | 0.505650 |
| 1 | 1 | 0.303538 |
#使用IsAlone 代替'Parch', 'SibSp', 'FamilySize'
train_df = train_df.drop(['Parch', 'SibSp', 'FamilySize'], axis=1)
test_df = test_df.drop(['Parch', 'SibSp', 'FamilySize'], axis=1)
combine = [train_df, test_df]
train_df.head()
| Survived | Pclass | Sex | Age | Fare | Embarked | Title | IsAlone | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 0 | 1 | 7.2500 | S | 1 | 0 |
| 1 | 1 | 1 | 1 | 2 | 71.2833 | C | 3 | 0 |
| 2 | 1 | 3 | 1 | 1 | 7.9250 | S | 2 | 1 |
| 3 | 1 | 1 | 1 | 2 | 53.1000 | S | 3 | 0 |
| 4 | 0 | 3 | 0 | 2 | 8.0500 | S | 1 | 1 |
同样的 年龄和Pclass 我门也可以放到一起,做一个人工特征
for dataset in combine:
dataset['Age*Class'] = dataset.Age * dataset.Pclass
train_df.loc[:, ['Age*Class', 'Age', 'Pclass']].head(10)
| Age*Class | Age | Pclass | |
|---|---|---|---|
| 0 | 3 | 1 | 3 |
| 1 | 2 | 2 | 1 |
| 2 | 3 | 1 | 3 |
| 3 | 2 | 2 | 1 |
| 4 | 6 | 2 | 3 |
| 5 | 3 | 1 | 3 |
| 6 | 3 | 3 | 1 |
| 7 | 0 | 0 | 3 |
| 8 | 3 | 1 | 3 |
| 9 | 0 | 0 | 2 |
现在让我们把分类特征也补充完整
#使用港口的众数填充缺失值
freq_port = train_df.Embarked.dropna().mode()[0]
for dataset in combine:
dataset['Embarked'] = dataset['Embarked'].fillna(freq_port)
train_df[['Embarked', 'Survived'
]].groupby(['Embarked'],
as_index=False).mean().sort_values(by='Survived', ascending=False)
| Embarked | Survived | |
|---|---|---|
| 0 | C | 0.553571 |
| 1 | Q | 0.389610 |
| 2 | S | 0.339009 |
#转换成数值型
for dataset in combine:
dataset['Embarked'] = dataset['Embarked'].map( {'S': 0, 'C': 1, 'Q': 2} ).astype(int)
train_df.head()
| Survived | Pclass | Sex | Age | Fare | Embarked | Title | IsAlone | Age*Class | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 0 | 1 | 7.2500 | 0 | 1 | 0 | 3 |
| 1 | 1 | 1 | 1 | 2 | 71.2833 | 1 | 3 | 0 | 2 |
| 2 | 1 | 3 | 1 | 1 | 7.9250 | 0 | 2 | 1 | 3 |
| 3 | 1 | 1 | 1 | 2 | 53.1000 | 0 | 3 | 0 | 2 |
| 4 | 0 | 3 | 0 | 2 | 8.0500 | 0 | 1 | 1 | 6 |
快速完成和转换的数字功能
现在,我们可以使用mode来完成测试数据集中单个缺失值的Fare特征,以获得该特征最频繁出现的值。我们只需要一行代码就可以完成。请注意,我们并没有创建一个中间的新特性,也没有做任何进一步的相关性分析来猜测丢失的特性,因为我们只替换了一个值。完成目标实现了模型算法对非空值操作的预期要求。我们可能还想把票价四舍五入到两个小数,因为它代表货币。
test_df['Fare'].fillna(test_df['Fare'].dropna().median(), inplace=True)
test_df.head()
| Pclass | Sex | Age | Fare | Embarked | Title | IsAlone | Age*Class | |
|---|---|---|---|---|---|---|---|---|
| 0 | 3 | 0 | 2 | 7.8292 | 2 | 1 | 1 | 6 |
| 1 | 3 | 1 | 2 | 7.0000 | 0 | 3 | 0 | 6 |
| 2 | 2 | 0 | 3 | 9.6875 | 2 | 1 | 1 | 6 |
| 3 | 3 | 0 | 1 | 8.6625 | 0 | 1 | 1 | 3 |
| 4 | 3 | 1 | 1 | 12.2875 | 0 | 3 | 0 | 3 |
#票价分组
train_df['FareBand'] = pd.qcut(train_df['Fare'], 4)
train_df[['FareBand', 'Survived'
]].groupby(['FareBand'],
as_index=False).mean().sort_values(by='FareBand',
ascending=True)
| FareBand | Survived | |
|---|---|---|
| 0 | (-0.001, 7.91] | 0.197309 |
| 1 | (7.91, 14.454] | 0.303571 |
| 2 | (14.454, 31.0] | 0.454955 |
| 3 | (31.0, 512.329] | 0.581081 |
#将票价特征转换为基于票价带的序数值
for dataset in combine:
dataset.loc[ dataset['Fare'] <= 7.91, 'Fare'] = 0
dataset.loc[(dataset['Fare'] > 7.91) & (dataset['Fare'] <= 14.454), 'Fare'] = 1
dataset.loc[(dataset['Fare'] > 14.454) & (dataset['Fare'] <= 31), 'Fare'] = 2
dataset.loc[ dataset['Fare'] > 31, 'Fare'] = 3
dataset['Fare'] = dataset['Fare'].astype(int)
train_df = train_df.drop(['FareBand'], axis=1)
combine = [train_df, test_df]
train_df.head(10)
| Survived | Pclass | Sex | Age | Fare | Embarked | Title | IsAlone | Age*Class | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 0 | 1 | 0 | 0 | 1 | 0 | 3 |
| 1 | 1 | 1 | 1 | 2 | 3 | 1 | 3 | 0 | 2 |
| 2 | 1 | 3 | 1 | 1 | 1 | 0 | 2 | 1 | 3 |
| 3 | 1 | 1 | 1 | 2 | 3 | 0 | 3 | 0 | 2 |
| 4 | 0 | 3 | 0 | 2 | 1 | 0 | 1 | 1 | 6 |
| 5 | 0 | 3 | 0 | 1 | 1 | 2 | 1 | 1 | 3 |
| 6 | 0 | 1 | 0 | 3 | 3 | 0 | 1 | 1 | 3 |
| 7 | 0 | 3 | 0 | 0 | 2 | 0 | 4 | 0 | 0 |
| 8 | 1 | 3 | 1 | 1 | 1 | 0 | 3 | 0 | 3 |
| 9 | 1 | 2 | 1 | 0 | 2 | 1 | 3 | 0 | 0 |
test_df.head(10)
| Pclass | Sex | Age | Fare | Embarked | Title | IsAlone | Age*Class | |
|---|---|---|---|---|---|---|---|---|
| 0 | 3 | 0 | 2 | 0 | 2 | 1 | 1 | 6 |
| 1 | 3 | 1 | 2 | 0 | 0 | 3 | 0 | 6 |
| 2 | 2 | 0 | 3 | 1 | 2 | 1 | 1 | 6 |
| 3 | 3 | 0 | 1 | 1 | 0 | 1 | 1 | 3 |
| 4 | 3 | 1 | 1 | 1 | 0 | 3 | 0 | 3 |
| 5 | 3 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 6 | 3 | 1 | 1 | 0 | 2 | 2 | 1 | 3 |
| 7 | 2 | 0 | 1 | 2 | 0 | 1 | 0 | 2 |
| 8 | 3 | 1 | 1 | 0 | 1 | 3 | 1 | 3 |
| 9 | 3 | 0 | 1 | 2 | 0 | 1 | 0 | 3 |
到此,我们完成了一份数据的制作,为接下来的建模做好了数据准备
建模、预测和解决问题
现在我们已经准备好训练模型并预测所需的解决方案了。
有60多种预测建模算法可供选择。我们必须了解问题的类型和解决方案的需求,将范围缩小到我们可以评估的少数几个模型。我们的问题是一个分类和回归的类问题,我们想要确定输出(是否存活)与其他变量或特征(性别、年龄、港口等)之间的关系。当我们用给定的数据集训练我们的模型时,我们也在进行一类被称为监督学习的机器学习。有了这两个标准-监督学习加上分类和回归,我们可以缩小我们的模型选择,包括:
- 逻辑回归
- SVM 支持向量机
- K近邻
- 朴素贝叶斯分类器
- 决策树
- 随机森林
- 感知机
- 人工神经网络
X_train = train_df.drop("Survived", axis=1)
Y_train = train_df["Survived"]
X_test = test_df.copy()
X_train.shape, Y_train.shape, X_test.shape
((891, 8), (891,), (418, 8))
#看下我们的数据
X_train
| Pclass | Sex | Age | Fare | Embarked | Title | IsAlone | Age*Class | |
|---|---|---|---|---|---|---|---|---|
| 0 | 3 | 0 | 1 | 0 | 0 | 1 | 0 | 3 |
| 1 | 1 | 1 | 2 | 3 | 1 | 3 | 0 | 2 |
| 2 | 3 | 1 | 1 | 1 | 0 | 2 | 1 | 3 |
| 3 | 1 | 1 | 2 | 3 | 0 | 3 | 0 | 2 |
| 4 | 3 | 0 | 2 | 1 | 0 | 1 | 1 | 6 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 886 | 2 | 0 | 1 | 1 | 0 | 5 | 1 | 2 |
| 887 | 1 | 1 | 1 | 2 | 0 | 2 | 1 | 1 |
| 888 | 3 | 1 | 1 | 2 | 0 | 2 | 0 | 3 |
| 889 | 1 | 0 | 1 | 2 | 1 | 1 | 1 | 1 |
| 890 | 3 | 0 | 1 | 0 | 2 | 1 | 1 | 3 |
891 rows × 8 columns
逻辑回归
逻辑回归是一个非常经典的算法,虽然被称为回归,但其实际上是一个分类模型,并常用于二分类。
优点:就是简单、可并行化、可解释强。
缺点:对于多重共线性很敏感,如果出现高相关的特征,需要使用因子分析、聚类分析等方法进行拆解降维。
log = LogisticRegression()
log.fit(X_train,Y_train)
Y_pre = log.predict(X_test)
acc_log = round(log.score(X_train, Y_train) * 100, 2)
acc_log
80.36
我们可以使用逻辑回归来验证我们之前创建的一些特征,这可以通过计算决策函数中特征的系数来实现。正系数增加响应的对数概率(从而增加概率),负系数降低响应的对数概率(从而降低概率)。
- 性别是最高的正相关系数,随着性别值的增加(男性:O到女性:1),存活的概率增加最多;
- 随着Pclass(1为最高级,3为最低级)的增加,存活的概率降低最大;
- 因此年龄*等级是一个很好的人工特征来建模,因为它与存活的负相关系数是第二高;
- 头衔是第二高的正相关系数。
pd.DataFrame(log.coef_)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0 | -0.7507 | 2.201619 | 0.287011 | -0.086655 | 0.261473 | 0.397888 | 0.126553 | -0.311069 |
coeff_df = pd.DataFrame(train_df.columns.delete(0))
coeff_df.columns = ['Feature']
coeff_df["Correlation"] = pd.Series(log.coef_[0])
coeff_df.sort_values(by='Correlation', ascending=False)
| Feature | Correlation | |
|---|---|---|
| 1 | Sex | 2.201619 |
| 5 | Title | 0.397888 |
| 2 | Age | 0.287011 |
| 4 | Embarked | 0.261473 |
| 6 | IsAlone | 0.126553 |
| 3 | Fare | -0.086655 |
| 7 | Age*Class | -0.311069 |
| 0 | Pclass | -0.750700 |
SVM支持向量机
已监督学习方式对数据进行二元分类的广义线性分类器,简单来说就是进行一个二分类,求解最优的那个分类面,然后用这个最优解进行分类
优点:鲁棒性强,对样本要求不高。
缺点:SVM的超参数需要通过交叉验证得到,非常耗费时间,而且SVM的核函数必须是正定的,计算量大,多分类很难使用。
#此处效果不是很好
svm = SVC()
svm.fit(X_train,Y_train)
Y_pred = svm.predict(X_test)
acc_svm = round(svm.score(X_train, Y_train) * 100, 2)
acc_svm
78.23
#线性SVM
linear_svc = LinearSVC()
linear_svc.fit(X_train, Y_train)
Y_pred = linear_svc.predict(X_test)
acc_linear_svc = round(linear_svc.score(X_train, Y_train) * 100, 2)
acc_linear_svc
79.12
KNN最近邻
knn是测量不同特征值之间的距离来进行分类,类似于近朱者赤近墨者黑,往往通过轮廓系数、交叉检验来找最优解
优点:简单易懂。
缺点:计算量大,对于不平衡样本处理起来较困难。
# 一般使用knn 是需要将数据进行标准化,消除量纲的影响(SVM等 需要计算距离的模型一般都要进行去量纲的操作)
Knn = KNeighborsClassifier()
Knn.fit(X_train,Y_train)
Y_pred = Knn.predict(X_test)
acc_Knn = round(Knn.score(X_train, Y_train) * 100, 2)
acc_Knn
83.95
朴素贝叶斯分类器
贝叶斯模型非常特殊,是一个概率模型,通过事件属性相关事件发生的概率(先验概率)去推测该事件发生的概率。
优点:对缺失数据不太敏感,算法也比较简单,常用于文本分类、邮件分类等。
缺点:贝叶斯是一个理论上的模型,主要是因为贝叶斯首先是假设各特征之间是相互独立,通常很难保证,还有先验概率通常是假设出来,并不一定准确。
值得一提的是贝叶斯网络,也称信念网络目前是最火热的模型之一,毕竟“信贝爷, 得永生”
# Gaussian Naive Bayes
bys = GaussianNB()
bys.fit(X_train, Y_train)
Y_pred = bys.predict(X_test)
acc_gaussian = round(bys.score(X_train, Y_train) * 100, 2)
acc_gaussian
72.28
决策树
决策树(分类树)是一种十分常用的分类方法,使用信息熵增益、信息熵增益率、Gini系数等进行剪枝寻求最优解
优点:可解释性强、对样本要求较低。
缺点:容易过拟合,寻求最优解往往会形成一个NP难(能在多项式时间内验证得出一个正确解)问题。
decision_tree = DecisionTreeClassifier()
decision_tree.fit(X_train, Y_train)
Y_pred = decision_tree.predict(X_test)
acc_decision_tree = round(decision_tree.score(X_train, Y_train) * 100, 2)
acc_decision_tree
86.76
Random forest 随机森林
随机森林是一个包含多个决策树的分类器, 并且其输出的类别是由个别树输出的类别的众数而定
优点:鲁棒性好,既可以分类又可以回归,准确度高。
缺点:黑盒模型、计算量大。
random_forest = RandomForestClassifier(n_estimators=100)
random_forest.fit(X_train, Y_train)
Y_pred = random_forest.predict(X_test)
random_forest.score(X_train, Y_train)
acc_random_forest = round(random_forest.score(X_train, Y_train) * 100, 2)
acc_random_forest
86.76
感知机
找一个超平面来分类
优点:简单。
缺点:通常只能用来二分类问题,对于非线性问题效果差。
perceptron = Perceptron()
perceptron.fit(X_train, Y_train)
Y_pred = perceptron.predict(X_test)
acc_perceptron = round(perceptron.score(X_train, Y_train) * 100, 2)
acc_perceptron
78.34
人工神经网络
人工神经网络就是模拟人思维的第二种方式。这是一个非线性动力学系统,其特色在于信息的分布式存储和并行协同处理。
优点:准。
缺点:黑盒模型、计算要求高,有时候可能比挖比特币更复杂,有时间跑神经网络我为什么不用来挖比特币呢。
ann = MLPClassifier()
ann.fit(X_train, Y_train)
Y_pred = lf.predict(X_test)
acc_ann = round(ann.score(X_train, Y_train) * 100, 2)
acc_ann
83.5
模型对比
对所有模型进行对比,选出最好的模型
# Random Forest和Decision Tree 评分相同 但是随机森林没有过拟合的问题,所以选择随机森林
models = pd.DataFrame({
'Model': ['Support Vector Machines', 'KNN', 'Logistic Regression',
'Random Forest', 'Naive Bayes', 'Perceptron',
'Artificial Neural Networks', 'Linear SVC',
'Decision Tree'],
'Score': [acc_svm, acc_Knn, acc_log,
acc_random_forest, acc_gaussian, acc_perceptron,
acc_ann, acc_linear_svc, acc_decision_tree]})
models.sort_values(by='Score', ascending=False)
| Model | Score | |
|---|---|---|
| 3 | Random Forest | 86.76 |
| 8 | Decision Tree | 86.76 |
| 1 | KNN | 83.95 |
| 6 | Artificial Neural Networks | 83.50 |
| 2 | Logistic Regression | 80.36 |
| 7 | Linear SVC | 79.12 |
| 5 | Perceptron | 78.34 |
| 0 | Support Vector Machines | 78.23 |
| 4 | Naive Bayes | 72.28 |
random_forest = RandomForestClassifier(n_estimators=100)
random_forest.fit(X_train, Y_train)
Y_pred = random_forest.predict(X_test)
X_test['Survived']=Y_pred
如果你懂了 你应该知道你能不能活下来(老凡尔赛了)
X_test[X_test['Survived']==1]
| Pclass | Sex | Age | Fare | Embarked | Title | IsAlone | Age*Class | Survived | |
|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 1 | 1 | 1 | 0 | 3 | 0 | 3 | 1 |
| 6 | 3 | 1 | 1 | 0 | 2 | 2 | 1 | 3 | 1 |
| 8 | 3 | 1 | 1 | 0 | 1 | 3 | 1 | 3 | 1 |
| 11 | 1 | 0 | 2 | 2 | 0 | 1 | 1 | 2 | 1 |
| 12 | 1 | 1 | 1 | 3 | 0 | 3 | 0 | 1 | 1 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 410 | 3 | 1 | 1 | 0 | 2 | 2 | 1 | 3 | 1 |
| 411 | 1 | 1 | 2 | 3 | 2 | 3 | 0 | 2 | 1 |
| 412 | 3 | 1 | 1 | 0 | 0 | 2 | 1 | 3 | 1 |
| 414 | 1 | 1 | 2 | 3 | 1 | 5 | 1 | 2 | 1 |
| 417 | 3 | 0 | 1 | 2 | 1 | 4 | 0 | 3 | 1 |
152 rows × 9 columns