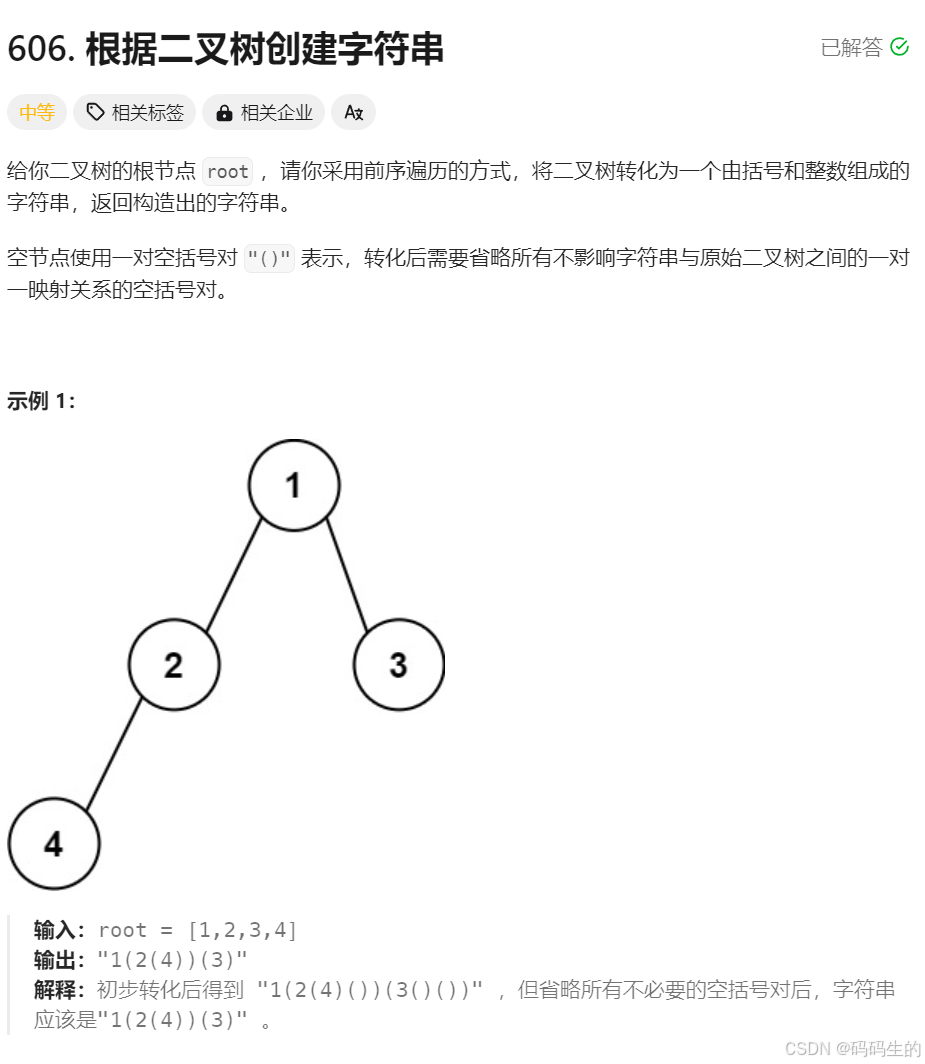
1.根据二叉树创建字符串
. - 力扣(LeetCode)
我的思路:
1. 根节点单独讨论,因为,根节点之后才会开始有括号
2.根节点的左孩子和右孩子分别进入operation函数
operation函数:
1.如果root不为空,先加(,再加root->val
2.分类讨论:
1.if(root->left==NULL&&root->right==NULL)
如果为叶子节点:直接加)
2.if(root->left==NULL&&root->right!=NULL)
如果左为空,右不为空;
无法省略括号,需要加()
3.如果左右都不为空
递归
operation(root->left,arr);
operation(root->right,arr);
最后加)
函数介绍:to_string,可将整形转换为string;
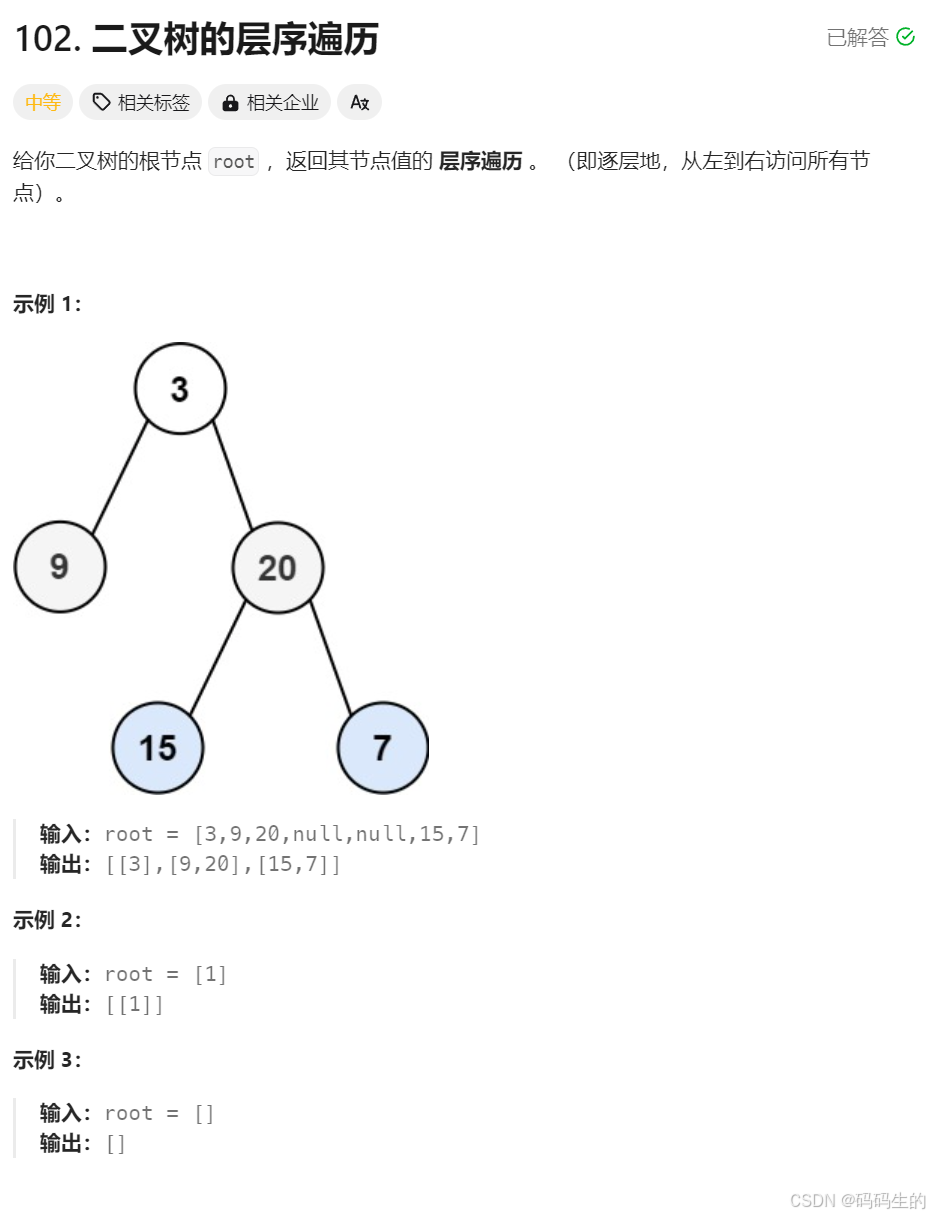
class Solution {public: void operation(TreeNode* root,string& arr) { if(root) { arr.push_back('('); arr+=to_string(root->val); if(root->left==NULL&&root->right==NULL) { arr.push_back(')'); } else { if(root->left==NULL&&root->right!=NULL) { arr.push_back('('); arr.push_back(')'); } operation(root->left,arr); operation(root->right,arr); arr.push_back(')'); } } } string tree2str(TreeNode* root) { string arr; if(root) { arr+=to_string(root->val); if(root->left==NULL&&root->right!=NULL) { arr.push_back('('); arr.push_back(')'); } operation(root->left,arr); operation(root->right,arr); } return arr; }};2.二叉树的分层遍历1
. - 力扣(LeetCode)
我的思路:
1. 建一个队列,并把根节点入队列,记录队列的大小;
2.while(size)
出队列,size--,并将左右节点入队列
3.size=队列的size;
4.若队列为空,则已经遍历完毕;
class Solution {public: vector<vector<int>> levelOrder(TreeNode* root) { TreeNode* tmp; vector<int> brr; vector<vector<int>> arr; queue<TreeNode*> it; int size=0; if(root!=NULL) { it.push(root); size++; } while(it.size()) { while(size) { tmp=it.front(); brr.push_back(tmp->val); it.pop(); size--; if(tmp->left) { it.push(tmp->left); } if(tmp->right) { it.push(tmp->right); } } arr.push_back(brr); brr.clear(); size=it.size(); } return arr; }};3.二叉树的分层遍历2
. - 力扣(LeetCode)
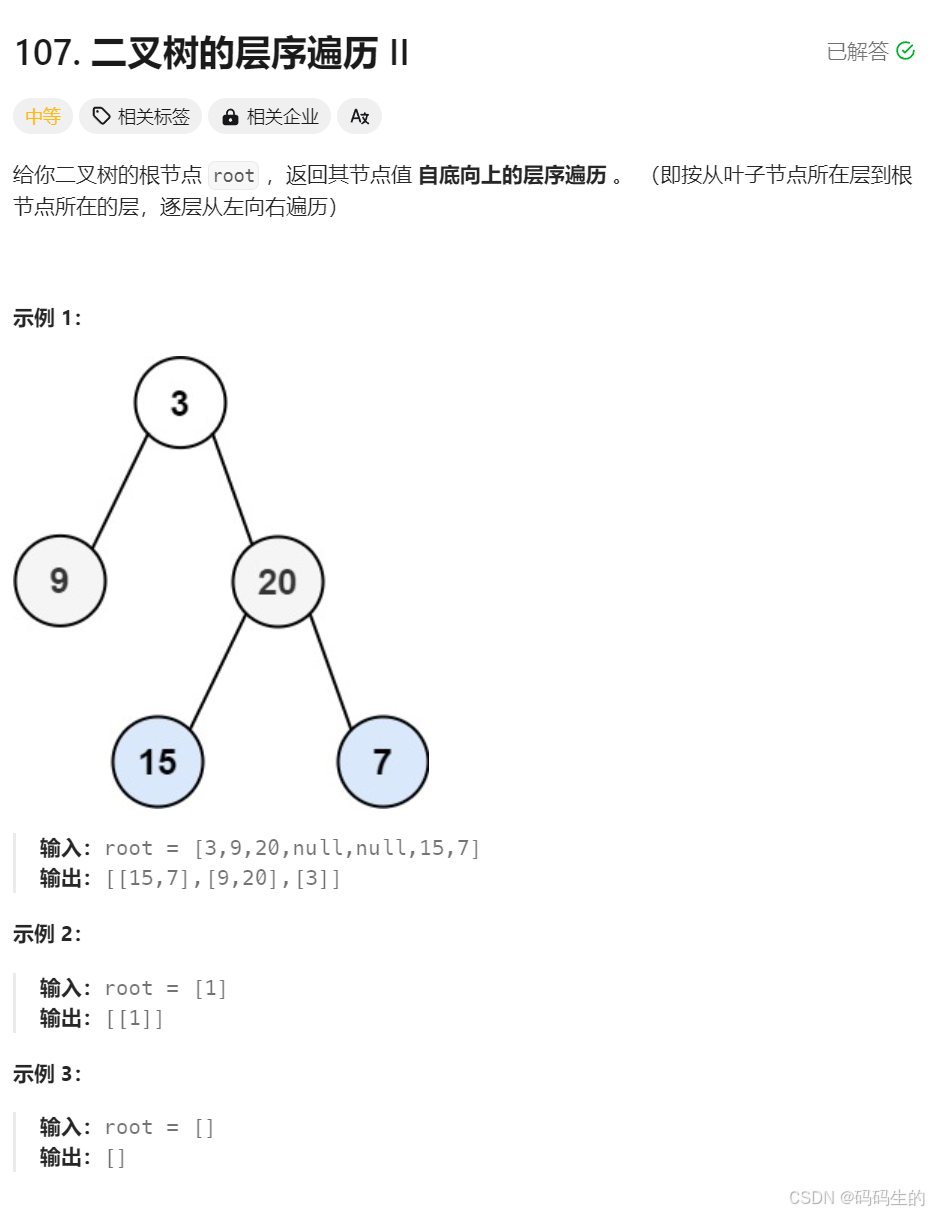
和前一题一样,只需在最后reverse(arr.begin(),arr.end());
class Solution {public: vector<vector<int>> levelOrderBottom(TreeNode* root) { TreeNode* tmp; vector<int> brr; vector<vector<int>> arr; queue<TreeNode*> it; int size=0; if(root!=NULL) { it.push(root); size++; } while(it.size()) { while(size) { tmp=it.front(); brr.push_back(tmp->val); it.pop(); size--; if(tmp->left) { it.push(tmp->left); } if(tmp->right) { it.push(tmp->right); } } arr.push_back(brr); brr.clear(); size=it.size(); } reverse(arr.begin(),arr.end()); return arr; }};4.最近公共祖先
. - 力扣(LeetCode)
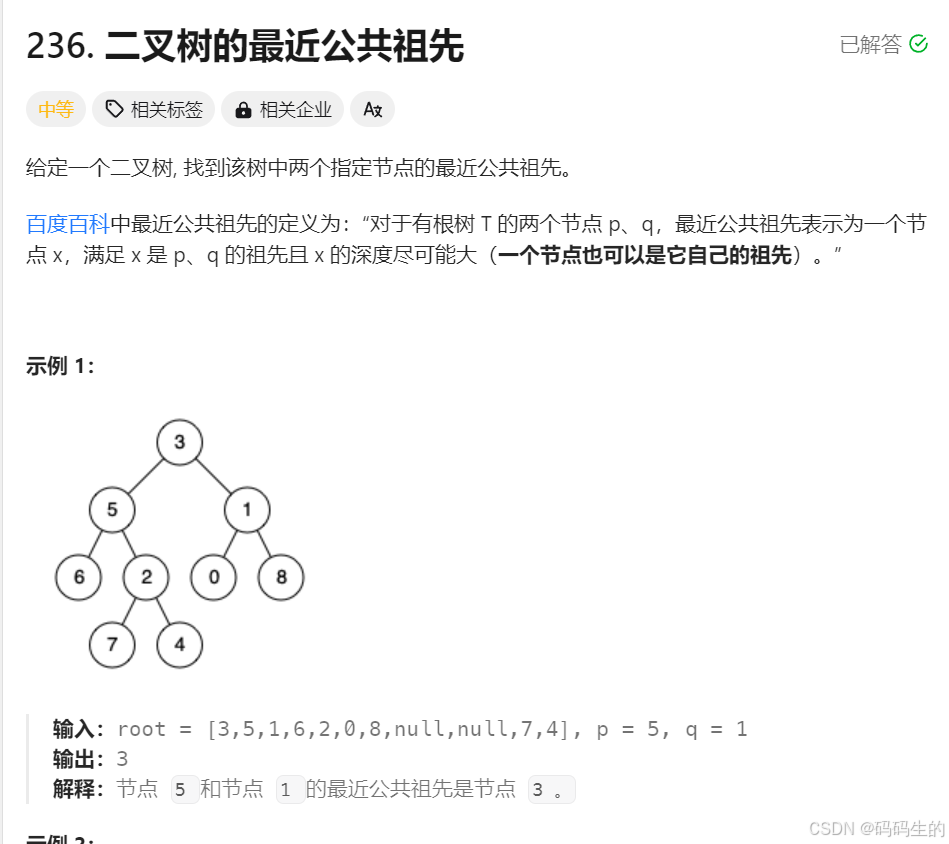
我的思路:
1.先写一个查找函数
2.从根节点开始查找p
3. 再从p开始查找q
如果找到了,返回p
如果没找到,那么p就变成p的父节点,再继续查找,直至从p可以找到q,返回p
class Solution {public: bool qfirstfind(TreeNode* p, TreeNode* q) { if(p==nullptr) return false; else if(p!=q) { if(qfirstfind(p->left, q)) return true; else return qfirstfind(p->right, q); } else if(p==q) return true; return 1; } //这个函数用来查找p之下是否有q void firstfind(TreeNode* p, TreeNode* q,TreeNode*&parent) { if(p!=nullptr) { if(p->left!=q&&p->right!=q) { firstfind(p->left, q,parent); firstfind(p->right, q,parent); } else { parent=p; //这里用来保存q的父节点 } } } void secondfind(TreeNode* root, TreeNode*&p, TreeNode*&q) { TreeNode* it; while((p->left!=q)&&(p->right!=q)&&(p!=root)) { firstfind(root,p,it); p=it; //p赋值为其父节点 if(qfirstfind(p,q)) { break; } } } TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { { if(qfirstfind(p,q)) return p; if(qfirstfind(q,p)) return q; //如果p,q有一个是公共祖先,则直接返回 secondfind(root, p, q); return p; } }};更好的的思路 !!!!!!!!:
用两个栈分别存放从根找到p,q的路径
1.若两个栈大小不一致
则用pop函数,保证二者大小一致
2.若两栈的top不一致,则二者都pop
直至两者的top相同,返回二者的top,即为最近的公共祖先
class Solution {public: bool findpath(TreeNode* root, TreeNode* x,stack<TreeNode*>&path) { if(root==nullptr) return false; path.push(root); if(root==x) return true; if(findpath(root->left,x,path)) return true; if(findpath(root->right,x,path)) return true; path.pop(); //走到这一步,证明root的左右子树都没有x,所以要把root删除 return false; } TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { stack<TreeNode*> ppath,qpath; findpath(root,p,ppath); findpath(root,q,qpath); while(ppath.size()!=qpath.size()) { if(ppath.size()>qpath.size()) ppath.pop(); else qpath.pop(); } while(ppath.top()!=qpath.top()) { ppath.pop(); qpath.pop(); } return ppath.top(); }};5.二叉树搜索树转换成排序双向链表
二叉搜索树与双向链表_牛客题霸_牛客网
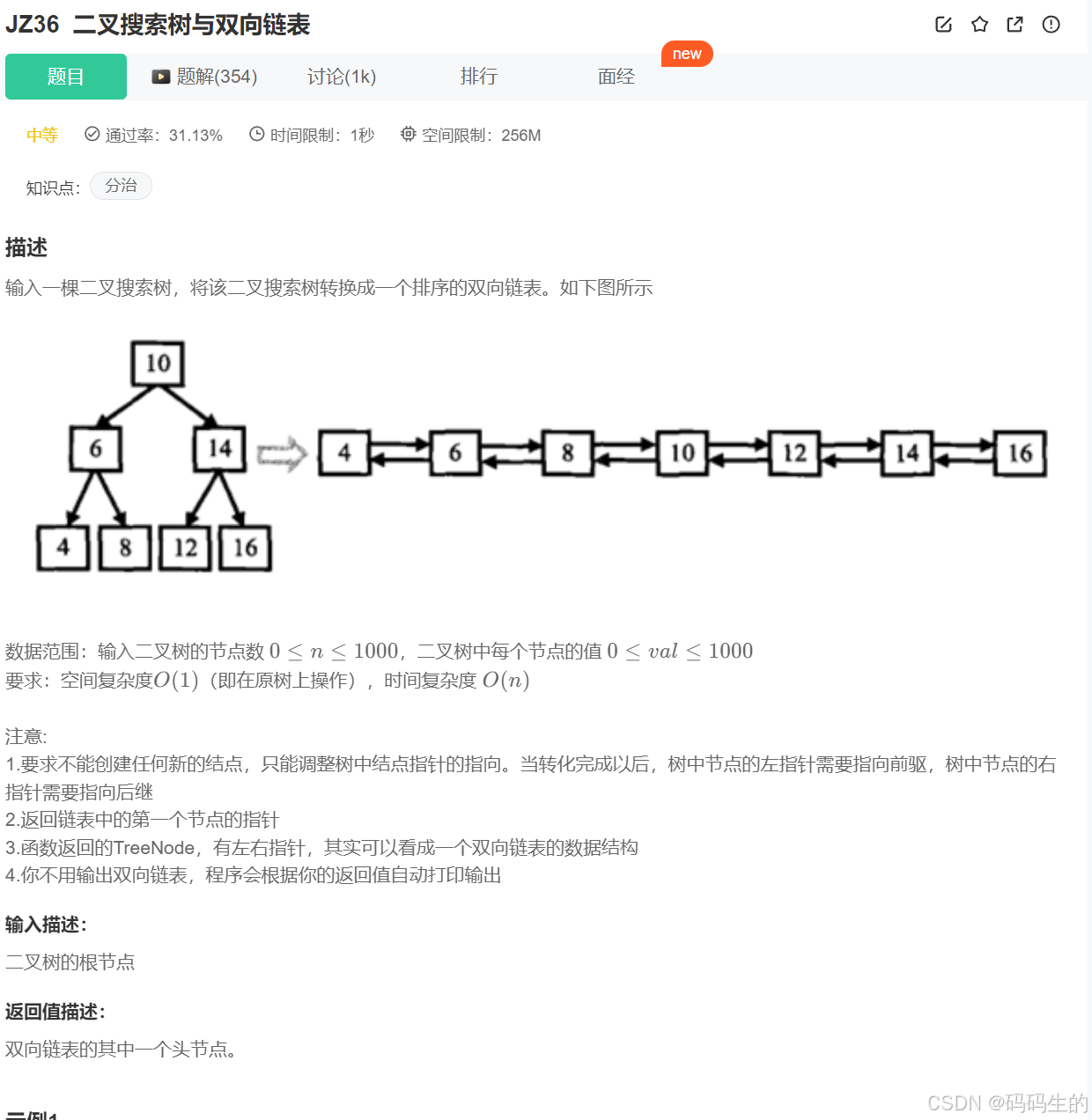
我的思路:
1.find1函数:寻找左子树中的最大值
2.find2函数:寻找右子树中的最小值
3.find3函数:寻找头节点,即二叉树中的最小值
从叶子节点开始连接
class Solution {public: void creat(TreeNode*root){if(root!=nullptr) {if(root->left==nullptr&&root->right==nullptr) {return; } else{ TreeNode*qleft=root->left; TreeNode*qright=root->right; creat(qleft);creat(qright); TreeNode*nleft=find1(root); TreeNode*nright=find2(root); if(nleft) nleft->right=root; if(nright) nright->left=root; root->left=nleft; root->right=nright; } }} TreeNode*find1(TreeNode*root) { TreeNode*it = root->left; if(it) //左右都不为空,找左子树最大的 {while (it->right) { it = it->right; } return it;}else {return nullptr;} }TreeNode*find2(TreeNode*root) { TreeNode*it = root->right; //左右都不为空,找右子树最小的 if(it) {while (it->left) { it = it->left; }return it; } else { return nullptr; } }TreeNode*find3(TreeNode*root) { //找根 TreeNode* it=root; while (it->left) { it = it->left; }return it; } TreeNode* Convert(TreeNode* pRootOfTree) { if(pRootOfTree==nullptr)return pRootOfTree;TreeNode*head=find3(pRootOfTree); creat(pRootOfTree); return head; }};6.前序中序还原二叉树
. - 力扣(LeetCode)
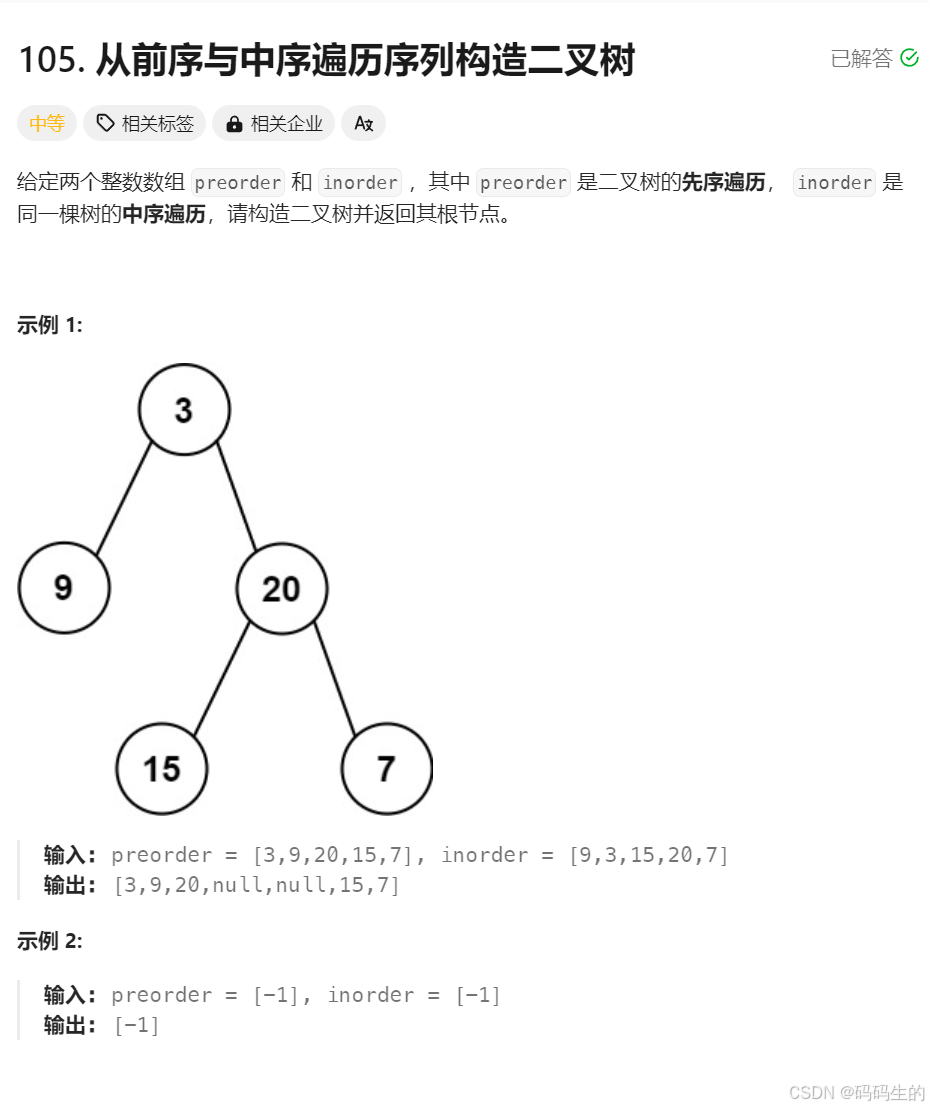
思路:
1.preorder 确定根
2.确定根了之后,将inorder分成两部分,左边为左子树,右边为右子树
3.分别递归左边和右边
class Solution {public: TreeNode* creat(vector<int>& preorder, vector<int>& inorder,int &prev,int begin,int end) { TreeNode* root; if(begin>end) return nullptr; int flag=preorder[prev]; int i=0; while(flag!=inorder[i]) { i++; } root=new TreeNode(flag); prev++; root->left=creat(preorder,inorder,prev,begin,i-1); //前序遍历,根左右,根后是左子树,所以先构建左子树 root->right=creat(preorder,inorder,prev,i+1,end); //有点类似并归排序 return root; } TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) { TreeNode* root; int prev=0; //前序遍历,从头开始找根 root=creat(preorder,inorder,prev,0,preorder.size()-1); return root; }};7.中序和后序还原二叉树
. - 力扣(LeetCode)
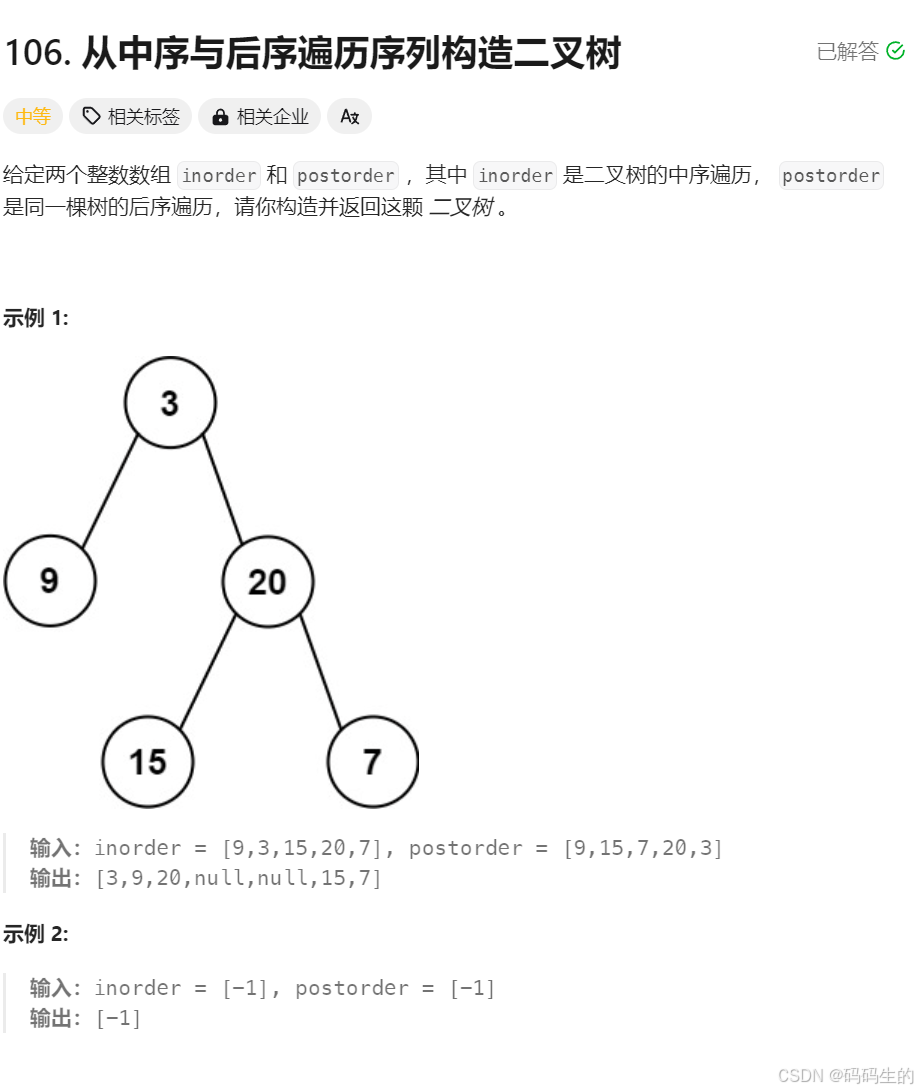
和上一题一样,中序确定左右子树
但不同的是得从后序遍历的尾开始找根,且根前是右子树
class Solution {public: TreeNode* creat(vector<int>& postorder, vector<int>& inorder,int &prev,int begin,int end) { TreeNode* root; if(begin>end) return nullptr; int flag=postorder[prev]; int i=0; while(flag!=inorder[i]) { i++; } root=new TreeNode(flag); prev--; root->right=creat(postorder,inorder,prev,i+1,end); //后序遍历左右根,倒着找的话,根的前面是右子树,所以右子树先建立 root->left=creat(postorder,inorder,prev,begin,i-1); return root; } TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) { TreeNode* root; int prev=inorder.size()-1; //从尾开始找根 root=creat(postorder,inorder,prev,0,inorder.size()-1); return root; }};