遗传算法的简单学习记录。
目录
一·优化问题
二·群体智能优化算法思想
三·遗传算法的产生
(一)简介
(二)基本概念和术语
(三)遗传算法与生物进化对比
四·遗传算法的组成
(一)编码
(二)适应度函数
(三)遗传算子
1.选择算子
2.交叉算子
3.变异算子
(四)运行参数
(五)遗传算法流程
五·应用实例
MATLAB遗传算法的工具箱使用
1.打开最优化工具箱optimization
2.配置
3.结果
一·优化问题
遗传算法实际上运用到了数学上优化问题的思想。
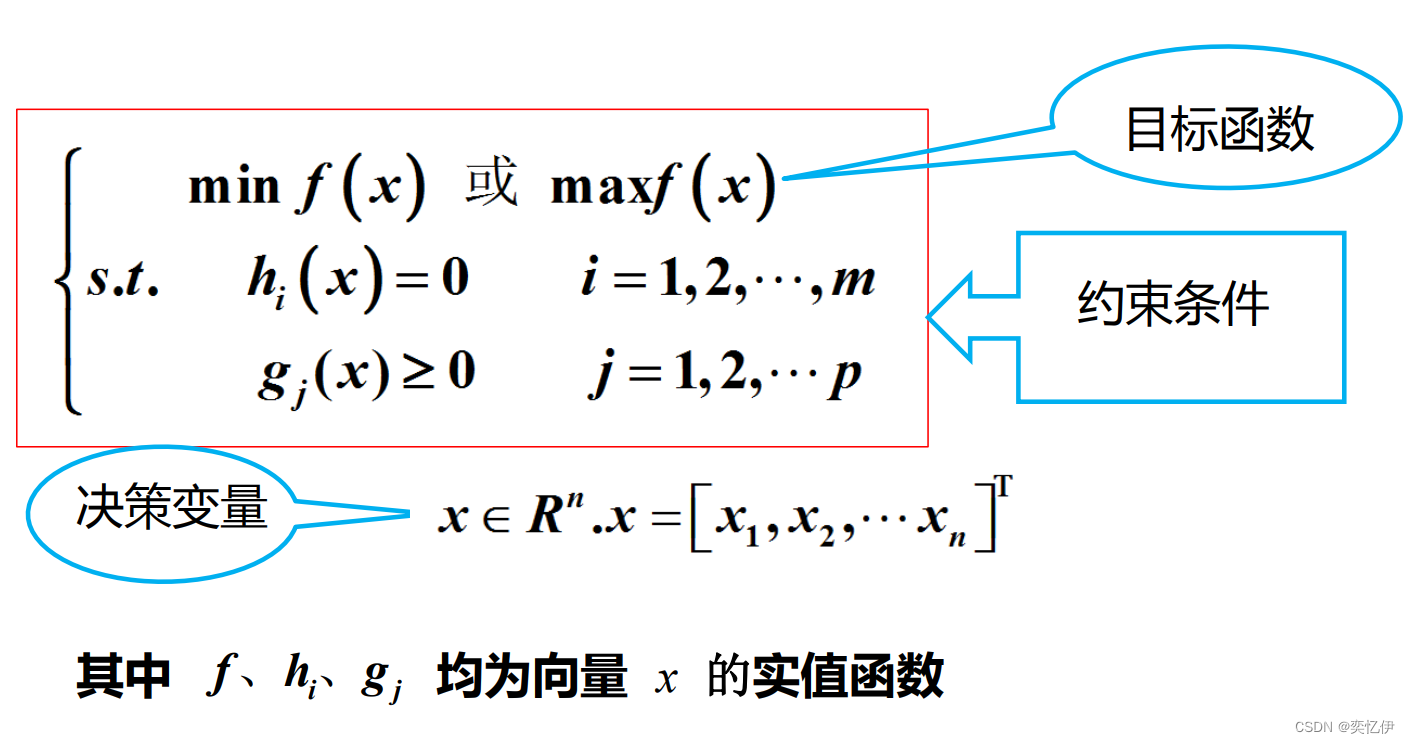
优化问题的三要素:目标函数、决策变量、约束条件。
二·群体智能优化算法思想
群体智能(Swarm Intelligence)优化算法是依靠模拟自然界中生物或非生物的群体行为对给定目标进行寻优(进化)的启发式搜索算法。
运用:遗传算法 , 模拟退火算法,粒子群算法,蜂群算法,蚁群算法,鱼群算法......
函数存在着很多的极大值和极小值。而最大值则是指定区间的极大值中的最大的那一个,把函数曲线理解成一个一个山峰和山谷组成的山脉。极大值像是一座座山峰,极小值则是像一座座山谷。这些山峰对应着局部最优解,其中有一个山峰是海拔最高的,这个山峰则对应的是全局最优解。
关于遗传算法,举个例子,有很多袋鼠,它们降落到喜玛拉雅山脉的任意地方。 这些袋鼠并不知道它们的任务是寻找珠穆朗玛峰。但每过几年,就在 一些海拔高度较低的地方射杀一些袋鼠。于是,不断有袋鼠死于海拔较低的地方,而在海拔越高的地方,袋鼠活得越久,也越有机会繁衍。就这样经过许多年,这些袋鼠们竟然都不自觉地聚拢到了一 个个的山峰上,可是在所有的袋鼠中,只有聚拢到珠穆朗玛峰的袋鼠 被带回了美丽的澳洲。
三·遗传算法的产生
(一)简介
• 遗传算法(Genetic Algorithm, GA)是由美国J. Holland教授于1975年在专著《自然界和人工系统的适应性》中首先提出。
• 借鉴生物界自然选择和自然遗传机制的随机化搜索算法。
• 其基本思想是模拟自然界遗传机制和生物进化论而形成的一种过程搜索全局最优解的算法。
(二)基本概念和术语
•遗传(heredity): 子代和父代具有相同或相似的性状,保证物种的稳定性
•变异(variation): 子代与父代,子代不同个体之间总有差异,是生命多样性的根源
•生存斗争和适者生存: 具有适应性变异的个体被保留,不具适应性变异的个体被淘汰
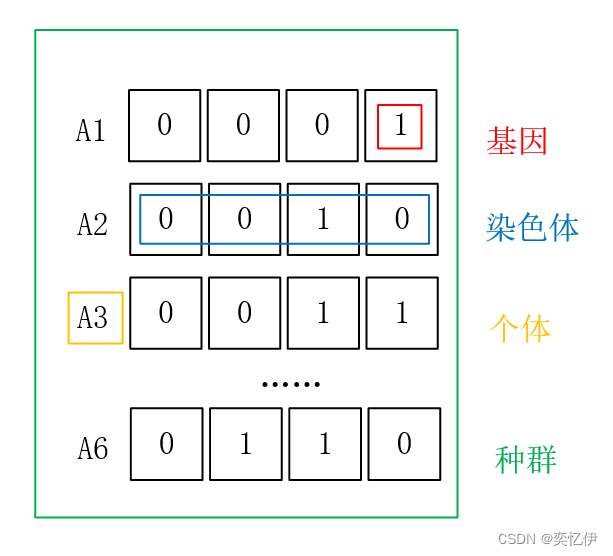
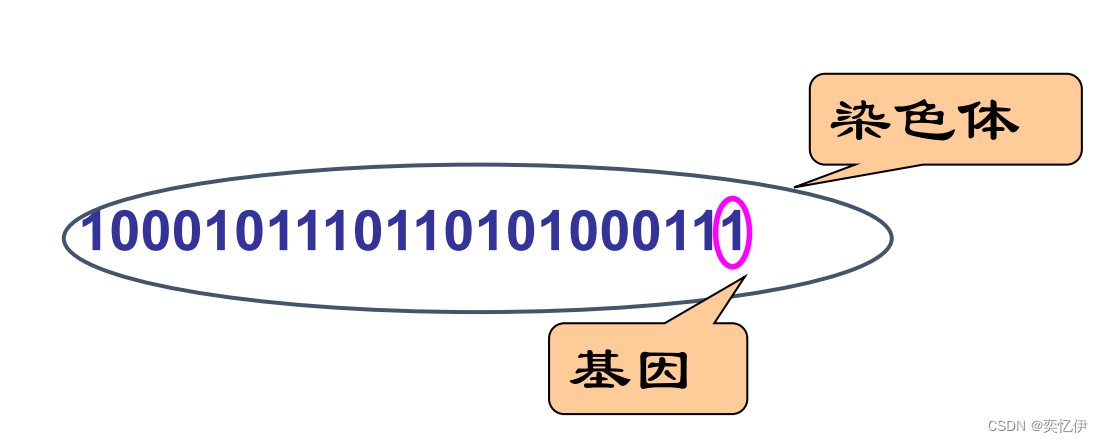
•基因(gene):染色体的一个片段
•染色体(Chromosome):由若干基因组成的位串 (问题中个体的某种字符串形式的编码表示)
•个体(individual):指染色体带有特征的实体 (问题的一个解,搜索空间中的一个点)
•种群(Population):个体的集合,该集合内的个体数称为种群的大小
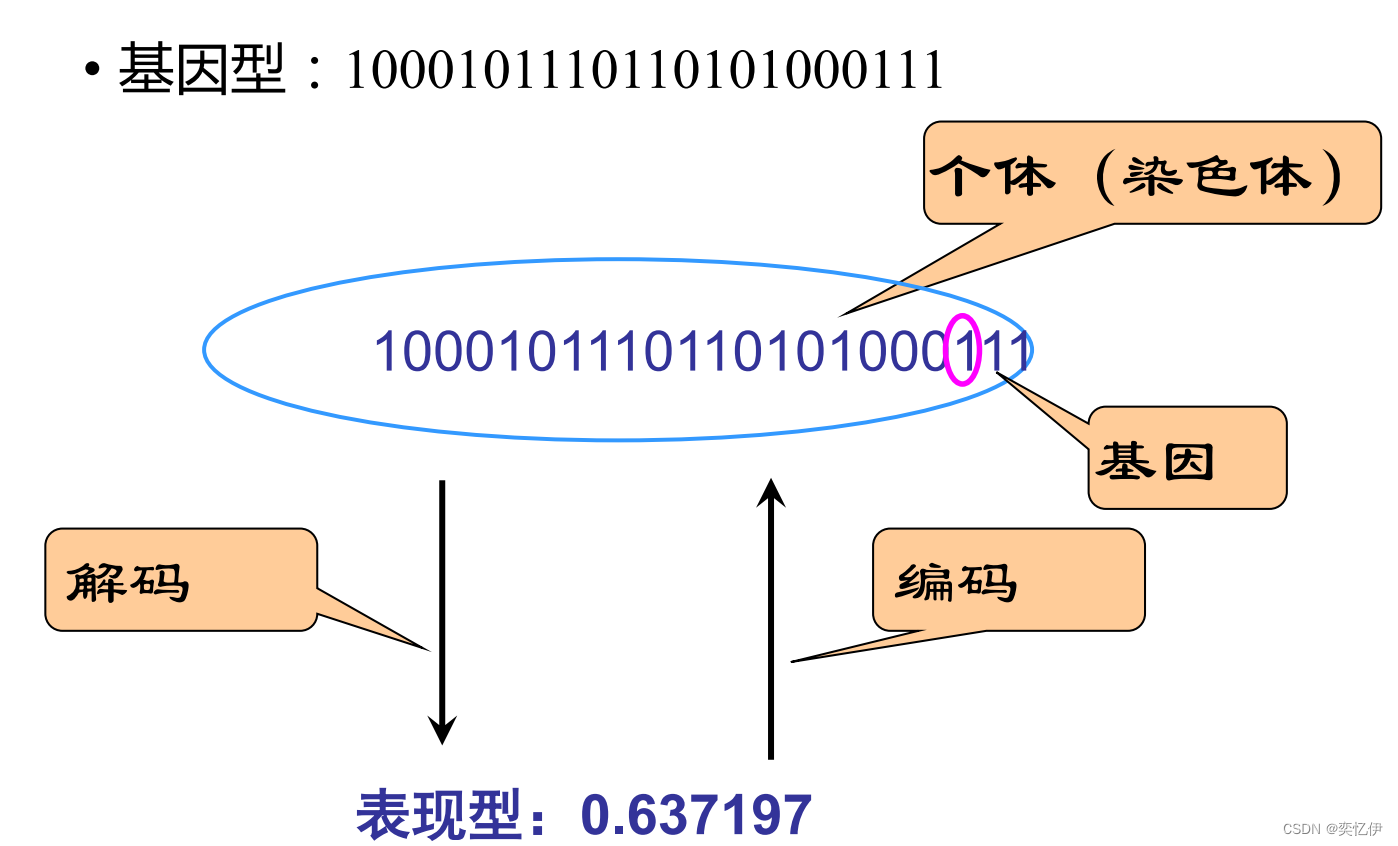
•基因型(genetype):基因组合的模型,染色体的内部表现
•表现型(phenotype):染色体决定性状的外部表现,根据基因型形成 的个体的外部表现
•编码(coding):从表现型到基因型的映射
•解码(decoding):从基因型到表现型的映射
•进化(evolution):个体逐渐适应生存环境,不断改良品质的过程。 生物的进化以种群的形式进行
•适应度(fitness):度量某个物种对于生存环境的适应程度
(三)遗传算法与生物进化对比

四·遗传算法的组成
(一)编码
• 遗传算法编码的目的是将已知对象转化为初始种群。
• 遗传算法以某种编码形式把对象转化为一串代码。
• 基本遗传算法(SGA)使用二进制串进行编码。
下面通过一个例子学习:

1.二进制编码要求取多少位?
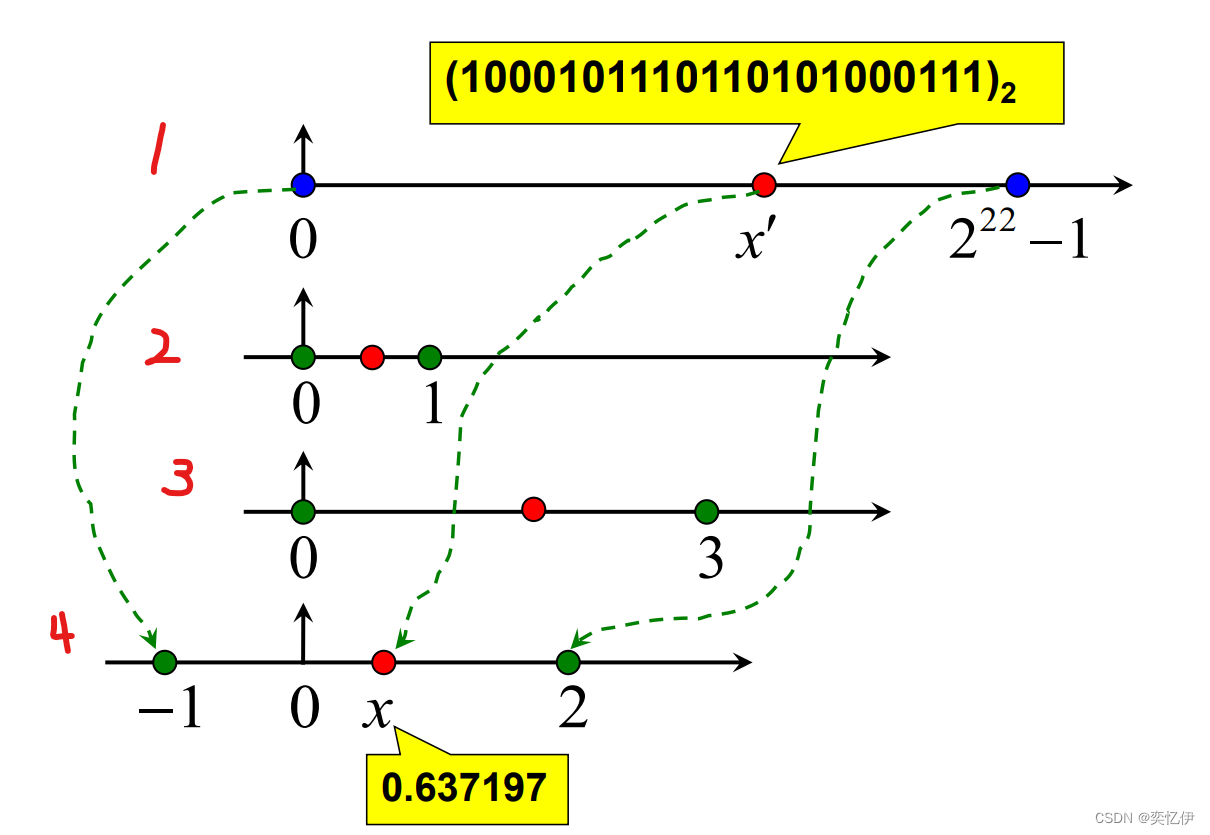
(1)区间长度为3,求解结果精确到6位小数,因此可将自变量 定义区间划分为3×10^6等份
(2)又因为2 ^21 < 3×10^6 < 2^22 ,所以二进制编码长度至少需要22位
(3)编码过程实质是将区间[-1,2]内对应的实数值转化为一个二进制串(b21b20b19b18…b1b0)
![]()
2.十进制实数与二进制编码之间应满足怎样的数学关系?

• 基本遗传算法(SGA)采用随机方法生成若干个个体的集合,该集合称为初始种群
• 初始种群的个体数量称为种群规模
(二)适应度函数
• 遗传算法中,个体的好坏由适应度函数来判断。个体带入适应度函数,函数值大,适应度高。
• 一般适应度函数的设计要求:单值、连续、非负
• 如果目标函数满足要求,可直接利用目标函数作为适应度函数
(最小化目标函数需要转化为最大化的适应度函数)
(三)遗传算子
遗传算子有三种:选择算子,交叉算子,变异算子。
1.选择算子
任务:对个体进行优胜劣汰操作,从父代群体中选取一些个体,遗传到 下一代群体。
结果:适应度高的个体被遗传到下一代群体中的概率大;适应度低的个体,被遗传到下一代群体中的概率小。
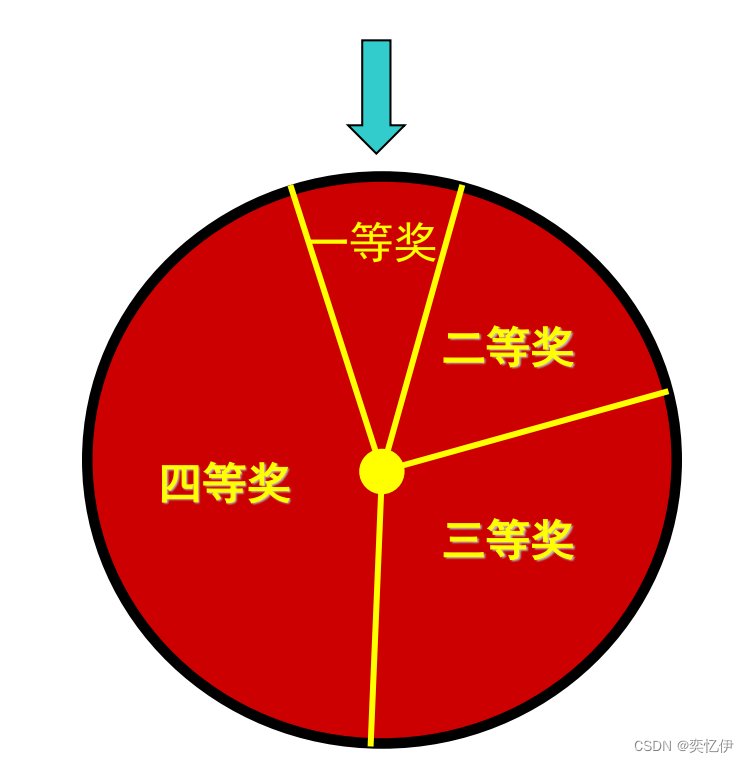
基本遗传算法(SGA)中选择算子采用轮盘赌(又称比例选择算子)选择方法。
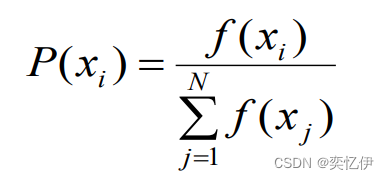
P是第i个个体的选择概率,f是第i个个体的适应度值。个体的选择概率与适应度函数成正比。上式相当于对适应度进行归一化处理。
要把这些个体放在圆盘上,并且所占面积需符合选中的概率P,也可以看成所占的弧长符合P。
假设圆盘的周长等于1,把个体按(选择概率*1)放在长度为1的线段上。
然后需要模拟选择的这个过程。先依次累加前面的概率,算出积累概率,然后从[0,1]的区间内,随机产生一组数a(n),计算机将这组数与积累概率依次比较,直到这个数a(j)大于积累概率,说明该个体被选中,换下一个数a(j+1)重复操作。
例如:
现有4个个体x1,x2,x3,x4,它们适应度分别为169,576,64,361
计算选择概率分别为0.14,0.49,0.06,0.31
放在线段上:
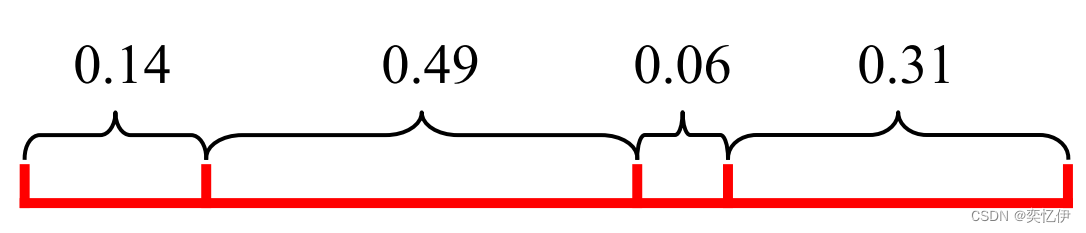
积累概率:
q1=0.14,q2=0.14+0.49=0.63,q3=0.14+0.49+0.06=0.69,q4=0.14+0.49+0.06+0.31=1
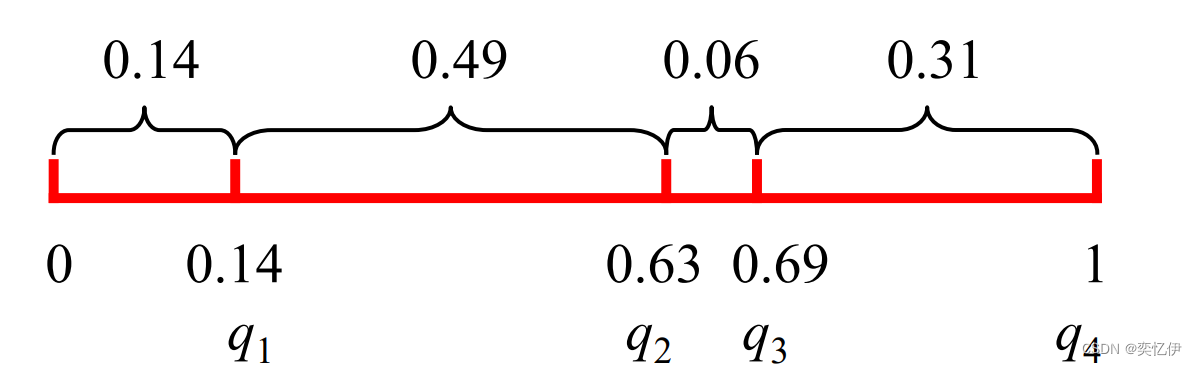
从区间[0, 1]中产生4个随机数:
r1 = 0.450126,r2 = 0.110347,r3 = 0.572496,r4 = 0.98503
r1大于q1小于q2,个体x2被选中1次;r2大于0小于q1,个体x1被选中1次;
r3大于q1小于q2,个体又x2被选中1次;r4大于q3小于q4,个体x4被选中1次。
综上结果如下:
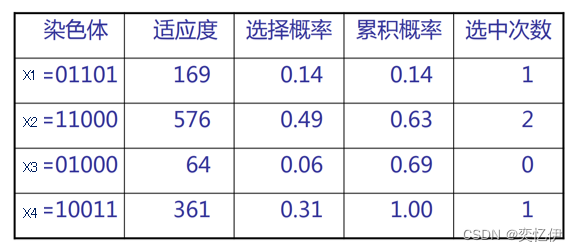
2.交叉算子
任务:对两个相互配对的染色体依据交叉概率按某种方式相互交换其部分基因,从而形成两个新的个体。
结果:产生新个体。
意义:交叉运算是遗传算法区别于其他进化算法的重要特征,它 在遗传算法中起关键作用,是产生新个体的主要方法。
交叉概率:用于判断两两个体是否需要交叉,如果随机数小于交叉概率,则两个个体进行交叉操作
基本遗传算法(SGA)中交叉算子采用单点交叉算子
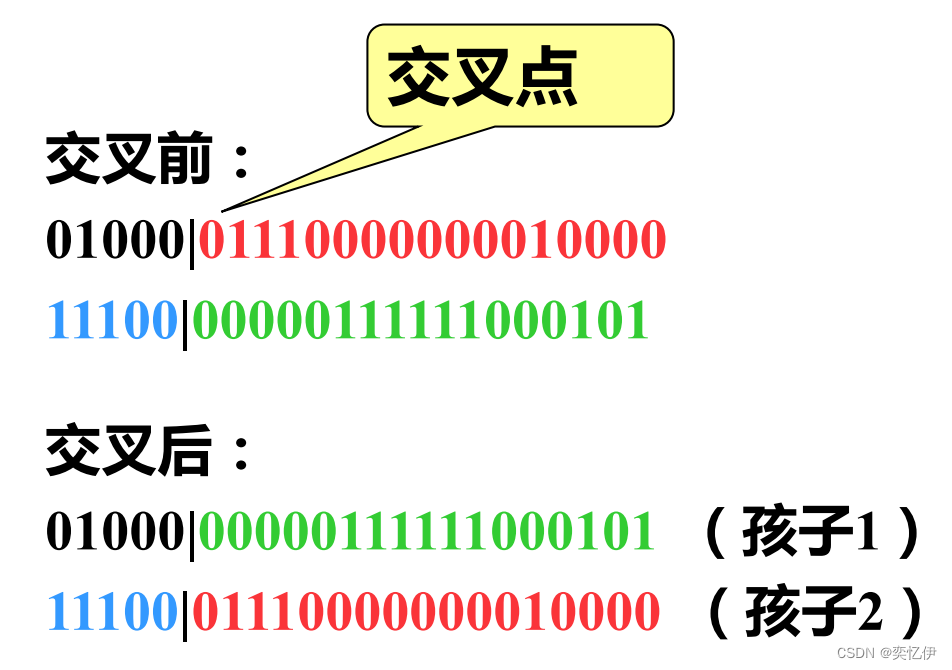
3.变异算子
任务:对个体编码串随机指定的某一位或某几位基因作变异运算。
结果:对于二进制编码符号串所表示的个体,若某一基因座上的原有基因值为0,则将其变为1;反之 ,若原有基因值为1,则将其变为0 。(基本位变异)
变异概率用于判断任一个体是否需要变异 。

(四)运行参数
1.M :种群规模
2.T :遗传运算的终止进化代数
3.Pc :交叉概率
4.Pm :变异概率
(五)遗传算法流程
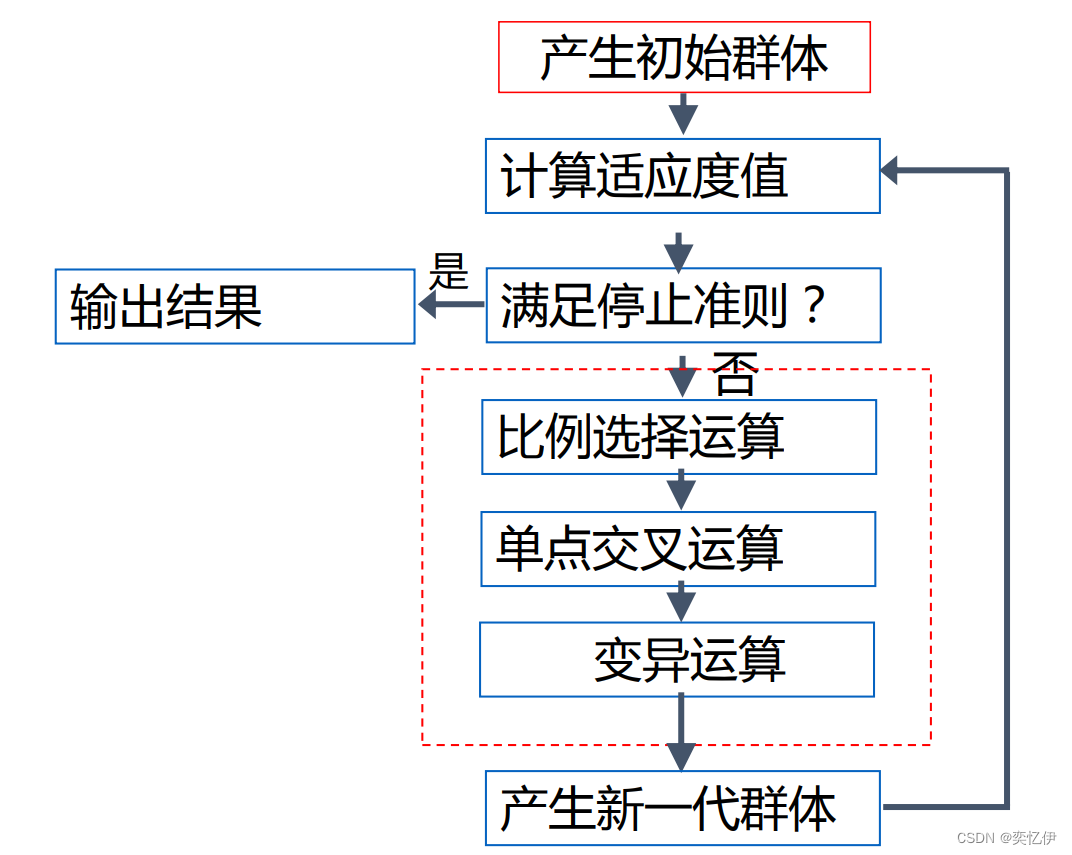
五·应用实例
MATLAB遗传算法的工具箱使用
用遗传算法求解 Ackley 函数的最小值问题
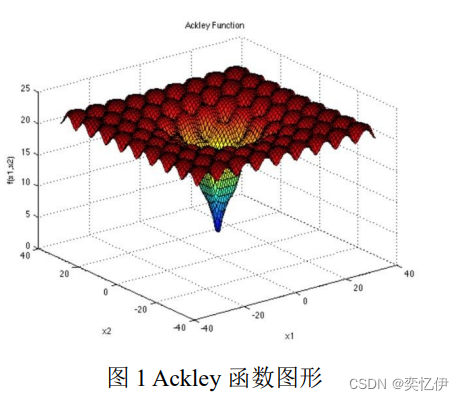
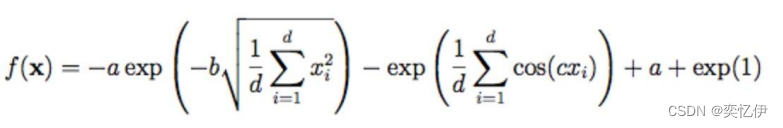
其中,a=20,b=0.2,c=2π,d=2。

1.打开最优化工具箱optimization
会弹出窗口说该工具箱已经搬家了,使用Optimize Live Editor代替,那就代替吧。
随后到了这个界面
往下滑到这里
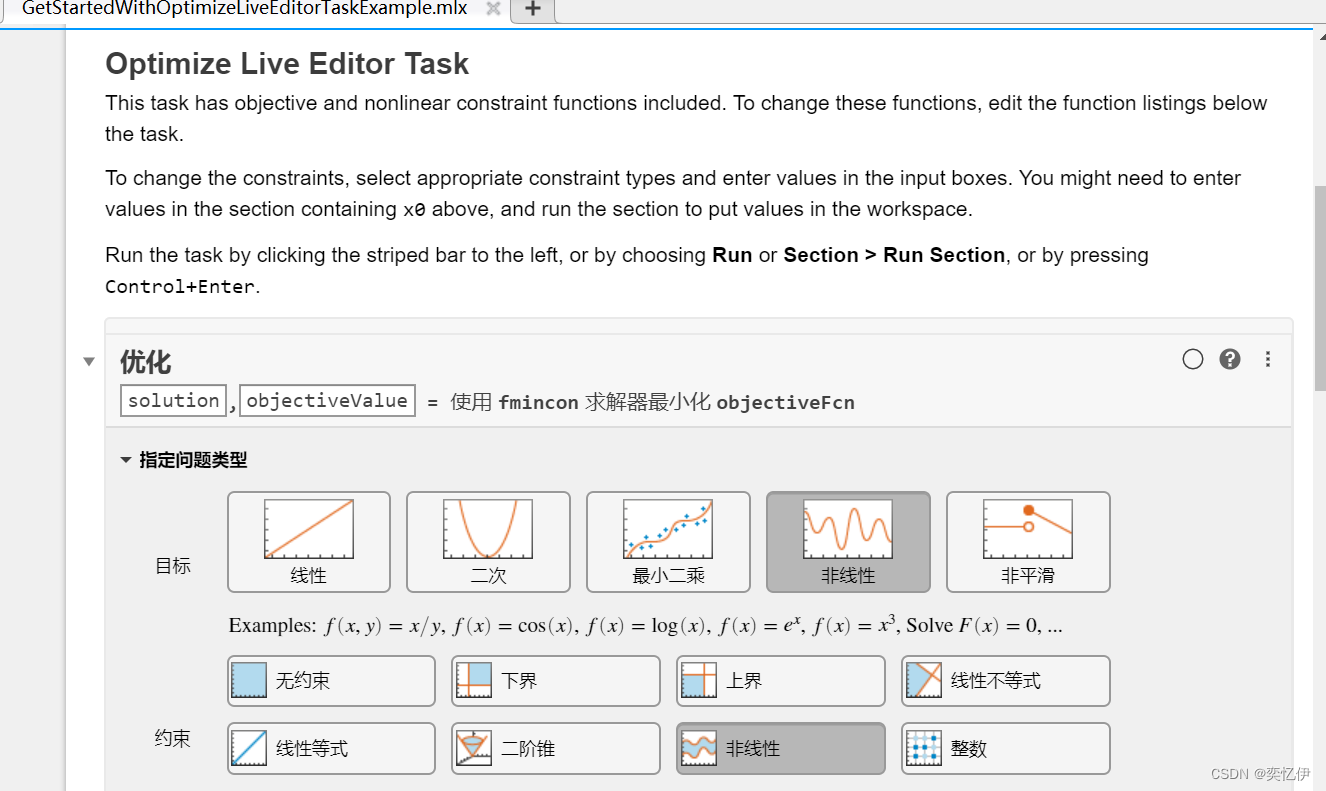
开始我们的编辑吧
2.配置
首先带入已知参数,简化我们的目标函数
f(x)=-20*exp(-0.2*sqrt(0.5*(x(1)^2+x(2)^2)))-exp(0.5*(cos(2*pi*x(1))+cos(2*pi*x(2))))+20+exp(1);我们的优化工具箱只能求最大值的优化问题,所以书写的时候要取反
写成函数文件objectiveFcn.m
function f= objectiveFcn(x)f1 = -20*exp(-0.2*sqrt(0.5*(x(1)^2+x(2)^2)))-exp(0.5*(cos(2*pi*x(1))+cos(2*pi*x(2))))+20+exp(1);%取反求最大值f=-f1;end我们还要在工作区准备几个变量:
①代表变量数目的变量:a=2 (可以从目标函数中知道有两个变量x1和x2)
②代表种群范围的变量:x=[-40;40] (系统要求为列向量)
回到编辑器
如图选择
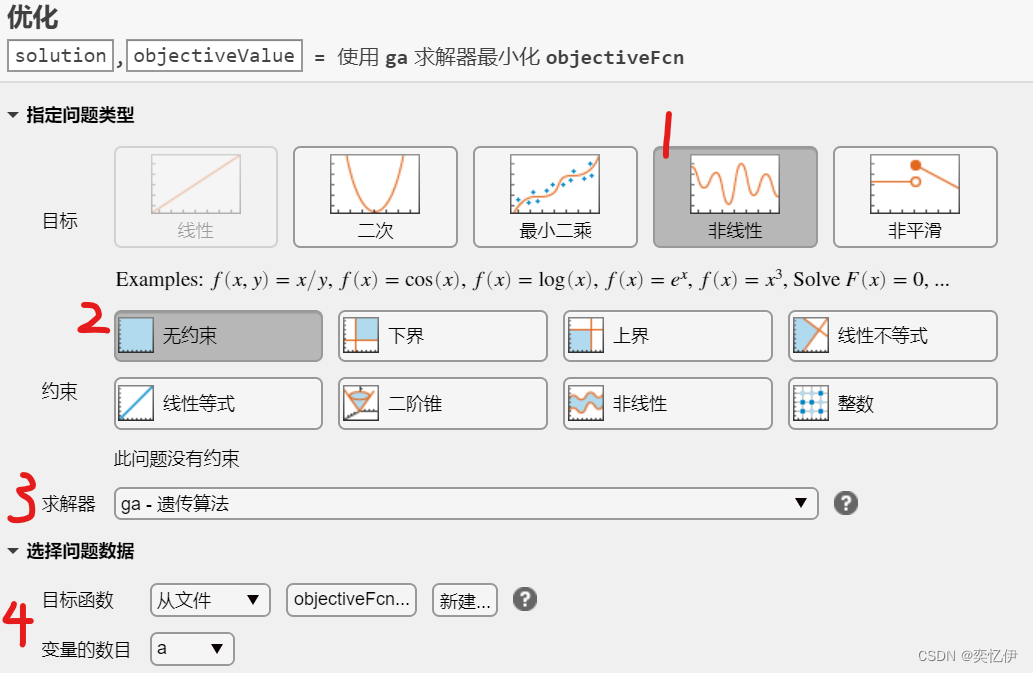
打开指定求解器选项

依次添加选项
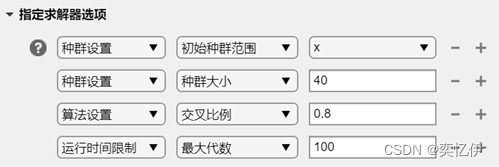
选择绘制最佳适应度
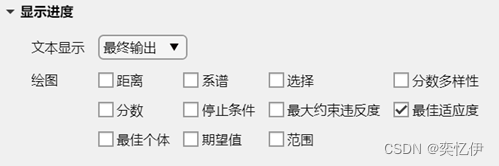
最后运行
3.结果
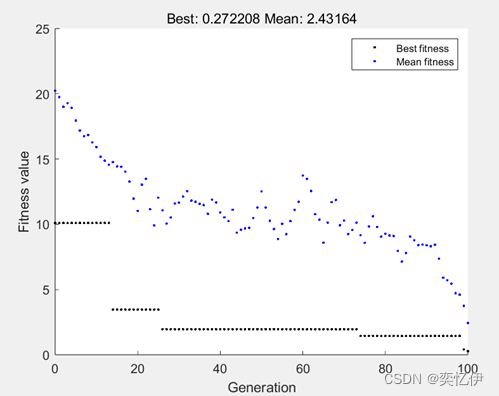
工作区出现如下结果,objectiveValue是最佳适应度,solution是最佳适应度对应的两个变量值。
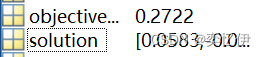
最佳适应度值和进化代数之间的关系图