选择题
?eg1
一棵有15个节点的完全二叉树和一棵同样有15个节点的普通二叉树,叶子节点的个数最多会差多少个()?
正确答案: C
A. 3 B. 5 C. 7 D. 9
解析:普通二叉树的叶子节点数最少为1 所以,而一棵完全二叉树最下面一层都是叶子节点,对于15个节点的完全二叉树,有 8 个叶子节点,因此最多会相差7个。
?eg2
一棵有 n 个结点的二叉树,按层次从上到下、同一层从左到右顺序存储在一维数组 A[1…n] 中,则二叉树中第 i 个结点(i从1开始用上述方法编号)的右孩子在数组 A 中的位置是( )
正确答案:D
A. A[2i](2i <= n)
B. A[2i + 1](2i + 1 <= n)
C. A[i - 2]
D. 条件不充分,无法确定
解析:
必须是完全二叉树才能确定,若是,选择B选项。图解如下:
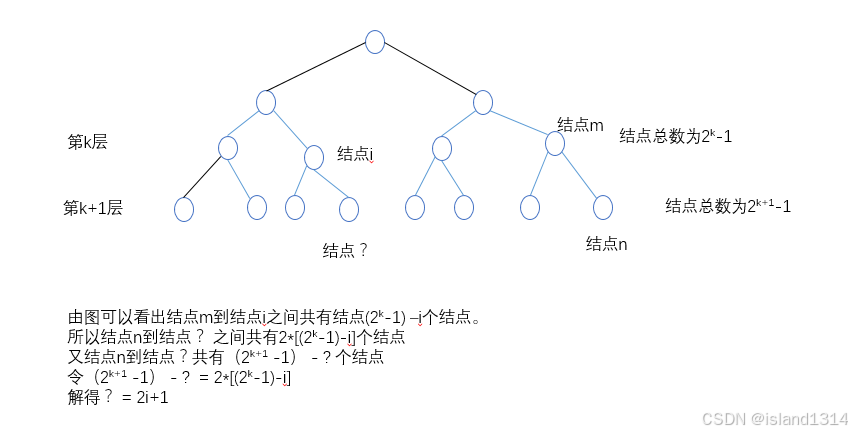
根据二叉树的性质5:
1.对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
1.1 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
1.2 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
1.3 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
上述的性质的节点从0开始编号, 而题目当中是从1开始编号, 所有右孩子的序号为 2i+1
?eg3
已知-算术表达式的中缀表达式为 a-(b+c/d)*e , 其后缀形式为( )
正确答案:D
A. -a+b*c/d
B. -a+b*cd/e
C. -+*abc/de
D. abcd/+e*-
解析:使用中缀表达式构建二叉树
第一个 “-”则将表达式分为左右子树, 左子树为“a”, 右子树为“(b+c/d)e”在1.1中的右子树“(b+c/d)e”, 通过“”将再次分为左右子树, 左子树为“(b+c/d)”, 右子树为“e”在1.2中的左子树“(b+c/d)”, 通过“+”将再次分为左右子树, 左子树为“b”, 右子树为“c/d”在1.3中的右子树“c/d”, 通过“/”将再次分为左右子树, 左子树为“c”, 右子树为“d”所以构建出来的二叉树如下图所示, 后缀表达式也就不难求解, 先左, 再右, 再根, 即“abcd/+e-”
?eg4
将一棵有100个结点的完全二叉树从根这一层开始,开始进行层次遍历编号,那么编号最小的叶节点的编号为(),则编号为 98 的节点的父节点编号为()。 (根节点为1)
正确答案:51, 49
解析:
由题意可知最小编号的叶子一定是最后一个节点的父节点的右兄弟节点,最后节点编号100,父节点编号为50,所以答案是51。
根节点是i,那么子节点是2i,2i+1,那么98,99的父节点就是49,
?eg5
设二叉树的先序遍历序列和后序遍历序列正好相反,则该二叉树满足的条件是()。
正确答案:B
A. 空或只有一个结点 B. 高度等于其结点数
C. 任一结点无左孩子 D. 任一结点无右孩子
解析:
A.如果是空,或者是只有一个结点那么先序遍历和后序遍历得到的序列是一样的。
C.在任何一个结点没有左孩子的时候
D.与C同理
B.满足每一层只有一个结点,即树高等于结点的数目时题目条件成立
先序遍历:根左右;后续遍历:左右根
要满足题意,则只有,根左<----->左根,根右<--------->右根
所以高度一定等于节点数
?eg6
某二叉树共有 399 个结点,其中 有199个为 度为2的 结点 ,则该二叉树中的叶子节点数为()
正确答案:C
A. 198 B. 199 C. 200 D. 201
解析:
由二叉树的性质可知:n2 = n0 + 1
故度为0 及叶子节点 比 度为2 (199) 多一个 ,答案为 200个
?eg7
在一颗度为3的树中,度为3的结点有2个,度为2的结点有1个,度为1的结点有2个,则叶子结点有( )个
正确答案:D
A. 7 B. 0 C. 7 D. 6
解析:
设度为i的节点个数为ni,则该树总共有n个节点
n = n0+n1+n2+n3.
有n个节点的树的总边数为 n-1条,根据度的定义,总边数与度之间的关系为
n-1 = 0n0+1n1+2n2+3n3
联立两个方程可得,n0 = n2 +2 n3+1, n0 =6.
?eg8
设一棵完全二叉树具有1000个结点,则此完全二叉树有()个度为2的结点。
正确答案:C
A. 497 B. 498 C. 499 D. 500
解析:
1、叶子结点:度为0的结点。
2、以n0代表度为0的结点,n2代表度为2的结点。
3、则根据二叉树的性质有 n0 = n2 +1。
1000个结点的完全二叉树有10层(2^9 - 1 < 1000 < 2 ^10 -1)
其中前9层为满二叉树,共有512-1=511个结点。因此有1000-511=489,说明第10层有489个结点,且第10层的结点均为叶子结点(度为0的结点)
而489/2 = 244…1,说明第9层有244+1(245)个结点有子结点,而根据满二叉树第9层共有 2^8 = 256个结点,则第9层度为0的结点(叶子结点)个数为 256-245 = 11。再由第一步所得叶子结点个数,可得二叉树中度为2的结点数为:n2=n0-1=500-1=499
即:度为2的结点数有499个
编程题
?eg1
从根到叶的二进制数之和
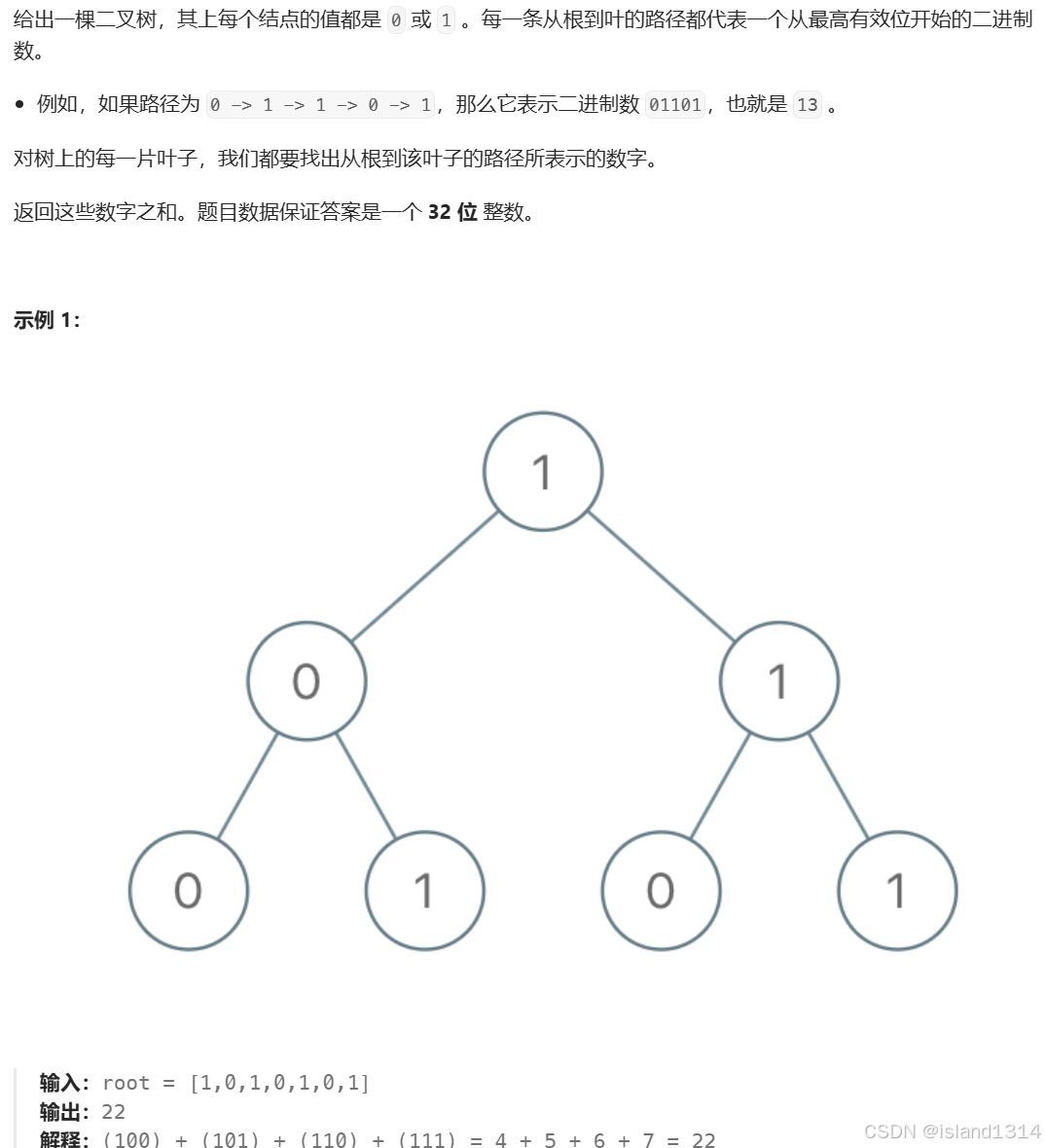
解析:
后序遍历的访问顺序为:左子树——右子树——根节点。我们对根节点 root 进行后序遍历:
如果节点是叶子节点,返回它对应的数字 val。
如果节点是非叶子节点,返回它的左子树和右子树对应的结果之和。class Solution {public: int dfs(TreeNode * root, int val){ if(root == nullptr) return 0; val = (val << 1) | root->val; //二进制转10进制 if(root->left == nullptr && root->right == nullptr) { //求叶子节点 return val; } return dfs(root->left, val) + dfs(root->right, val); } int sumRootToLeaf(TreeNode* root) { return dfs(root, 0); }};?eg2
二叉树的坡度
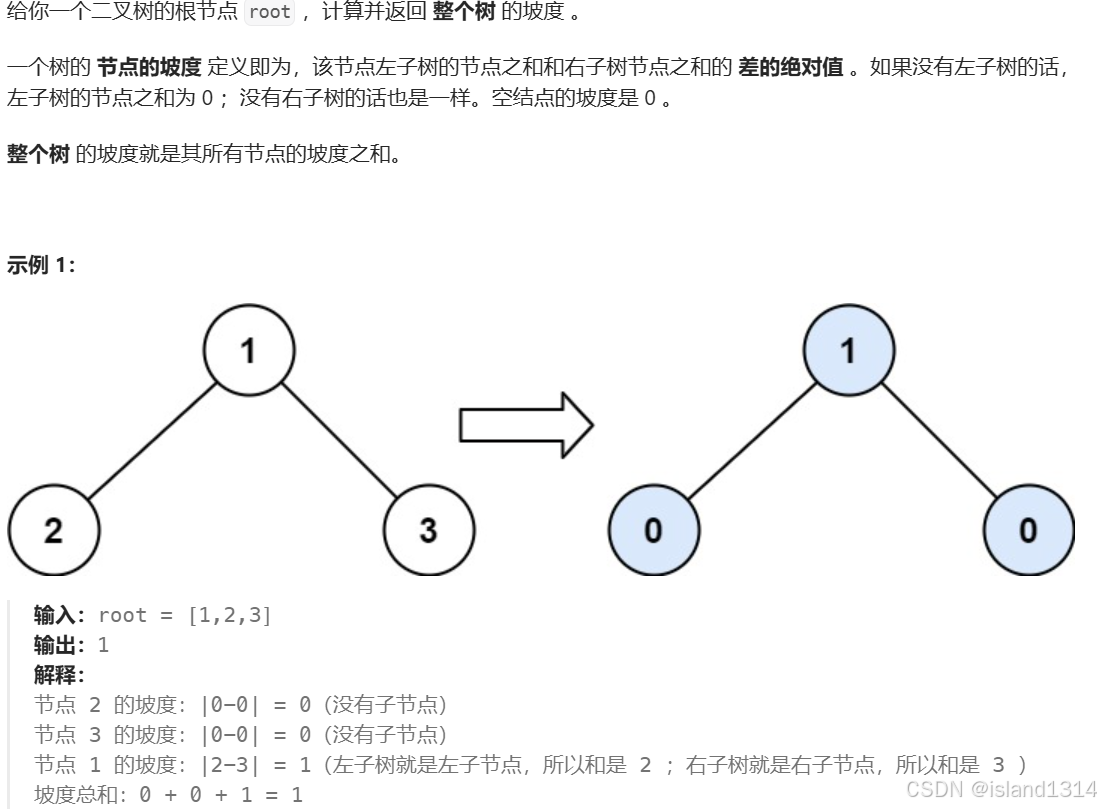
解析:dfs,在遍历每个结点时,累加其左子树结点之和与右子树结点之和的差的绝对值,并返回以其为根结点的树的结点之和。
从根结点开始遍历
遍历 root 的左子结点,得到左子树结点之和 sl;遍历 root 的右子结点,得到右子树结点之和 sr;
将左子树结点之和与右子树结点之和的差的绝对值累加到结果变量 ans;返回以 root 作为根结点的树的结点之和 sl + sr + node.valclass Solution {public: int ans = 0; int dfs(TreeNode* root){ if(root == nullptr) return 0; int sl = dfs(root->left); int sr = dfs(root->right); ans += abs(sl - sr); return sl + sr + root->val; } int findTilt(TreeNode* root) { dfs(root); return ans; }};?eg3
奇偶树
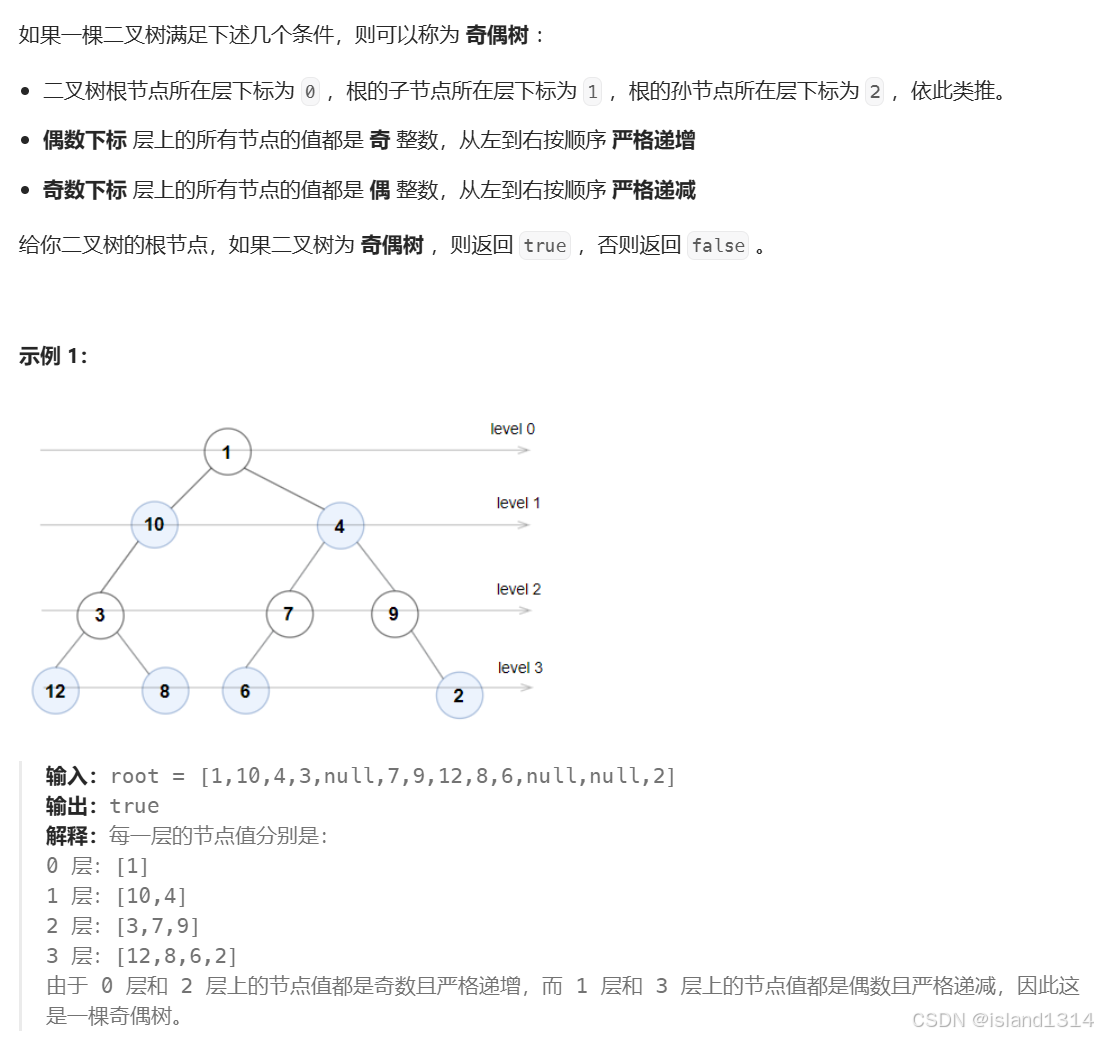
解析:
根据题意可知,我们需要根据 层 遍历这棵树,因此使用宽度优先搜索BFS遍历二叉树。
首先可以将root放入队列中,由于root的level=0,所以从其出发的可以直接到达点的level=1,将root从队列中弹出,然后将level=1的点放入队列中,因此现在队列的所有节点的level=1。
每次将下一层节点放入队列的时候,优先将左边先放入队列,这样就可以保证每一层是从左往右顺序的。
重复上面过程,所以从level=1出发的点,可以直接到达level=2。
在遍历每一层的时候,根据规则判断是否满足奇偶树的性质。
如果当前 层是偶数,首先判断数字的奇偶性,设prev的默认值为0,根据数字大小判断是否满足严格递增,并修改pre
prev的默认值为106+1,根据数字大小判断是否满足严格递减,并修改pre。 class Solution {public: bool isEvenOddTree(TreeNode* root) { queue<TreeNode*> q; q.push(root); int level = 0; while(!q.empty()){ int sz = q.size(); int pre = level == 0 ? 0 : 1e6 + 1; for(int i = 0; i < sz; i++){ TreeNode* next = q.front(); q.pop(); // 偶数递减 奇数递增 if((level == 0 && next->val <= pre) || (level == 1 && next->val >= pre)) return false; //奇偶 if((level == 0 && next->val % 2 == 0) || (level == 1 && next->val % 2 == 1)) return false; pre = next->val; if(next->left) q.push(next->left); if(next->right) q.push(next->right); } level ^= 1; } return true; }};