ARCH和GARCH简介
之前介绍过的ARIMA模型是假定随机扰动的方差是恒定的,这有时候难以适应现实中的金融时间序列模型,如下图所示:

我们发现大的波动往往会聚集在一起,这不符合同方差的假设。
所以我们通过引入条件异方差代替恒定方差的假定,构建了自回归条件异方差模型(ARCH),为了能应用ARCH或GARCH模型,我们须检验时间序列是否存在条件异方差。
H0:不存在ARCH效应; H1:存在ARCH效应
ARCH(1)模型是最简单的GARCH模型
ARCH(1):
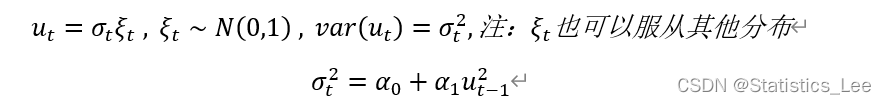
在ARCH1模型下,条件方差是自回归的,即ut的方差由ut滞后一期的平方值决定,在此我们以股票收益率去理解这个模型,假若ut为股票收益率,若昨天风平浪静,没有任何重大的干扰股市的新闻,那么ut-1理应波动不大,既然ut-1不大,那么ut当天的方差波动也不大,今天跟昨天差不多是小波动,若发生重大时间,严重影响股市收益率,则ut-1应较大,那么ut当天的方差波动也会变大,这种大波动跟着大波动,小波动跟着小波动的现象称为波动聚集
ARCH(q):
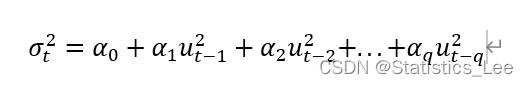
GARCH(p,q)(广义自回归条件异方差模型),GARCH模型相较与ARCH模型进一步引入了方差的滞后项:
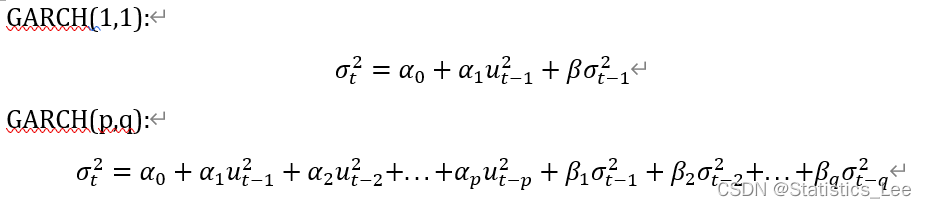
注:GARCH(1,1)模型足以捕捉大多数情况下的波动聚集
这里我们以微软的股价为例,构建ARCH及GARCH模型
基于ARCH和GARCH模型的微软股价收益率的R语言建模
加载包
list.packages<-c("fGarch", "PerformanceAnalytics","rugarch","tseries","xts","FinTS")invisible(lapply(list.packages, require, character.only = TRUE))new_data <- read.csv("C:\\Users\\X-BUNLEE\\Desktop\\Microsoft(1).csv")head(new_data) 
new_data$Dates <- as.Date(new_data$Dates,"%d/%m/%Y")#转换为时间序列数据new_data.z <- zoo(x=new_data$Close,order.by = new_data$Dates)#计算对数收益率并去除第一个值return_new_data <- Return.calculate(new_data.z,method = "log")[-1]ADF检验
library(urca)ADF_Returns <- ur.df(return_new_data, type = "drift",selectlags = "AIC" )summary(ADF_Returns)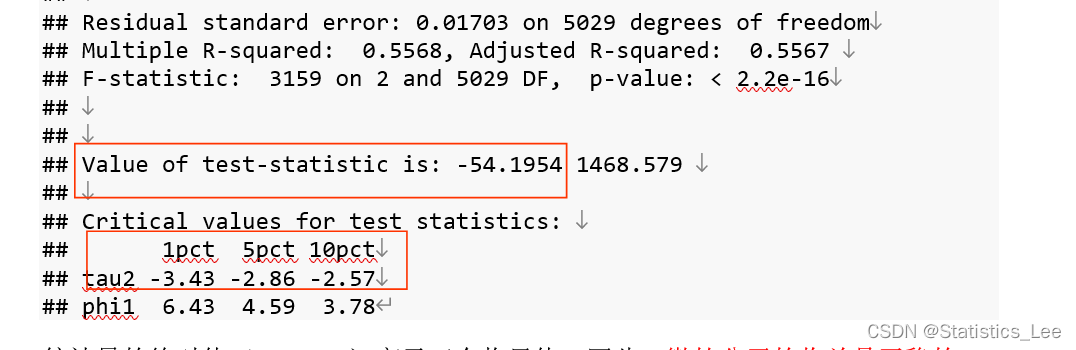
统计量的绝对值(54.1954)高于三个临界值。因此,微软公司的收益是平稳的
检查波动聚集
我们通过对数收益率,平方收益率,绝对收益率来观察波动的聚集性
dataplot <- cbind(return_new_data,return_new_data^2,abs(return_new_data))colnames(dataplot) <- c("对数收益率","平方收益率","绝对收益率")plot.zoo(dataplot,main = "微软的每日收益率",col = "blue") 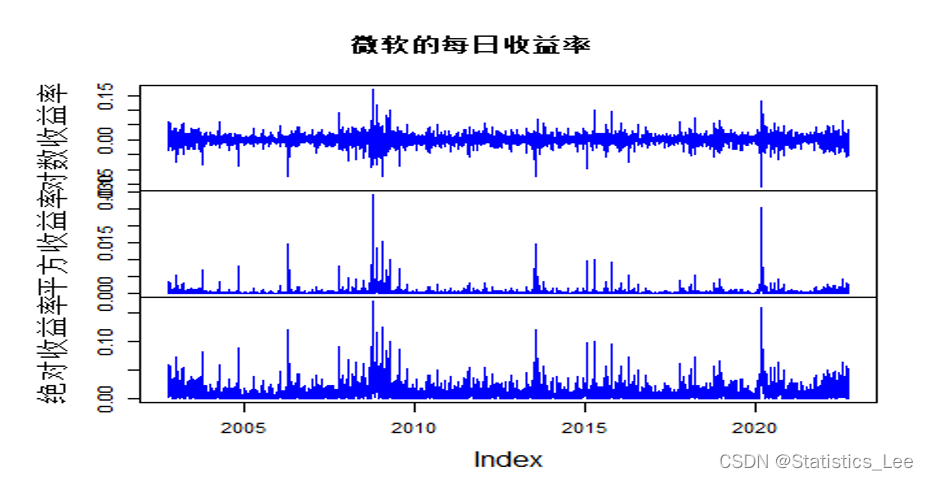
从上图我们可以看到明显的波动聚集情况(即大波动跟着大波动,小波动跟着小波动)
检查正态性
qqnorm(return_new_data,main = "微软每日收益率-QQ图",col = "blue")qqline(return_new_data) 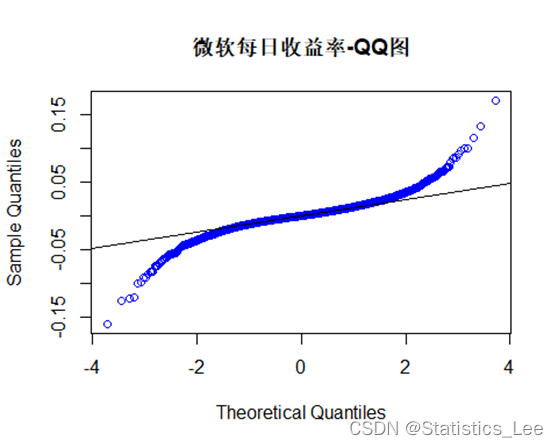
收益率似乎不服从正态分布,进一步给出数据常用的描述性统计,并进行Jarque-Bera检验检验数据正态性如下:
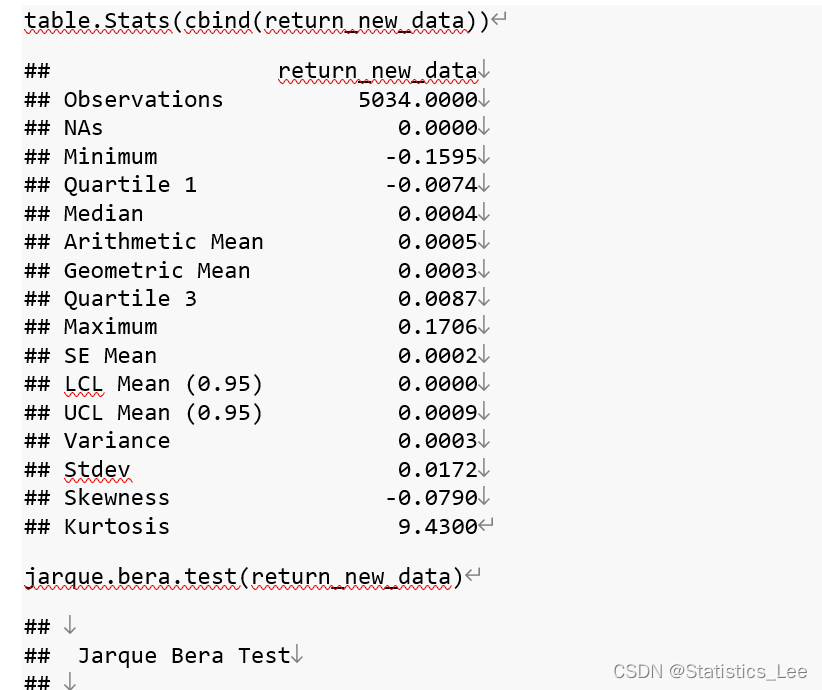

由于jarque.bera检验的p-value<2.2e-16,我们拒绝原假设,认为在0.01的显著性水平下,数据不服从正态分布
arch效应的检验
#将数据转换为xts类型return_new_data<- as.xts(return_new_data)#绘制对数回报率,平方回报率,绝对回报率的自相关系数图options(repr.plot.width=15, repr.plot.height=5)#指定图形宽度及高度par(mfrow=c(1,3))acf(return_new_data,main = "对数收益率")acf(return_new_data^2,main = "平方收益率")acf(abs(return_new_data),main = "绝对收益率") 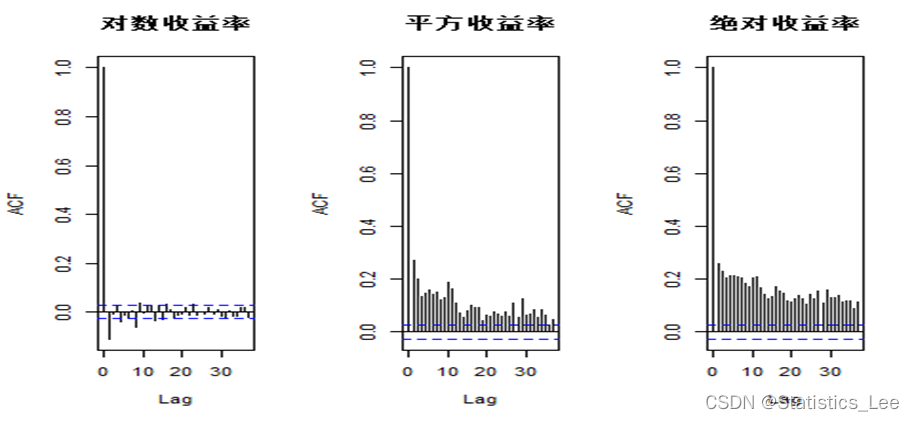
平方收益率和绝对收益率均展现出较高水平的自相关系数,接着对平方收益率进行Ljung-Box 检验以检验自相关性是否显著

由于p-value小于0.01,所以我们认为平方收益率存在着显著的自相关性,接着我们对对数收益率进行ARCH效应的检验如下:
ArchTest(return_new_data) 
由于p-value远小于0.01,认为对数收益率可以进行arch建模
估计正态扰动下的ARCH和GARCH模型
#mean.model意味拟合均值模型,arch模型也可以视作在均值模型的基础上对方差进行修正
# distribution.model="norm"意味ξt服从正态分布
spec <- ugarchspec(variance.model = list(garchOrder = c(1,0)), mean.model = list(armaOrder=c(0,0)),distribution.model="norm")#mean.model意味拟合均值模型,arch模型也可以视作在均值模型的基础上对方差进行修正 # distribution.model="norm"意味ξ_t 服从正态分布#拟合ARCH模型arch_model <- ugarchfit(data=return_new_data,spec = spec)arch_model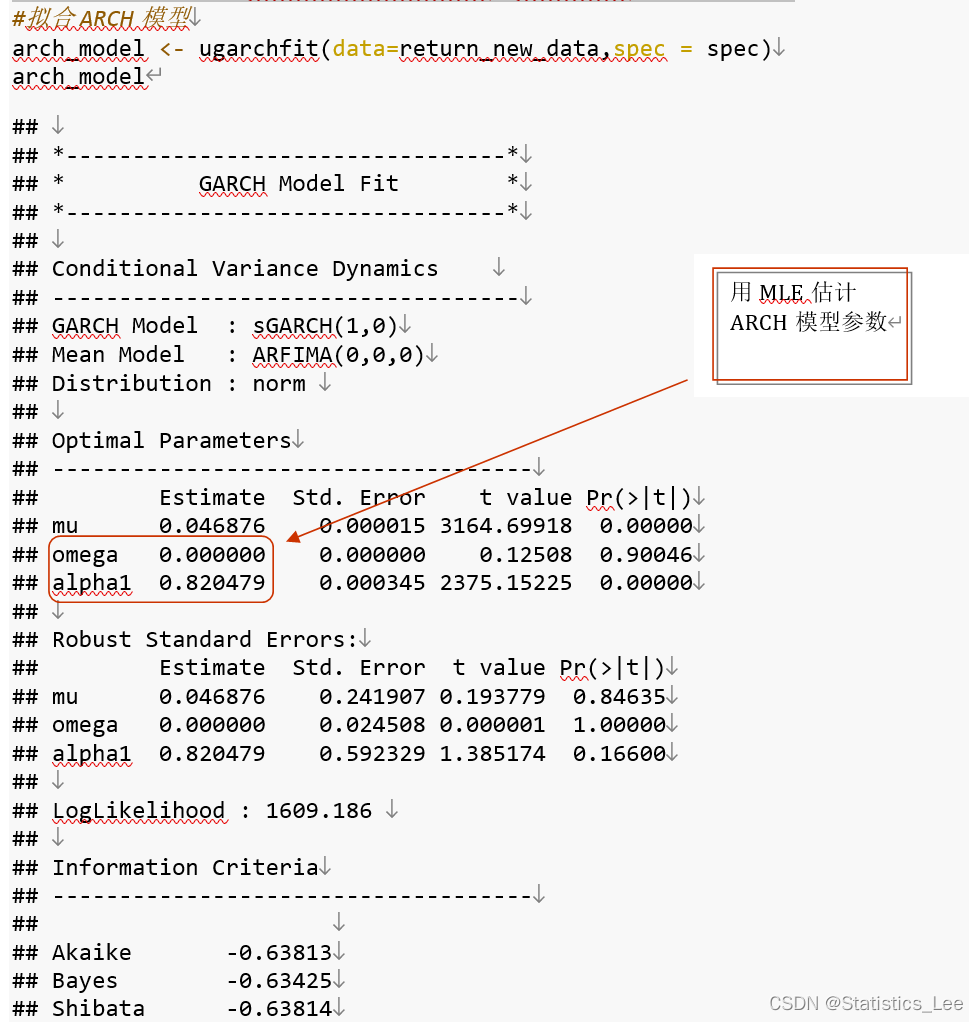
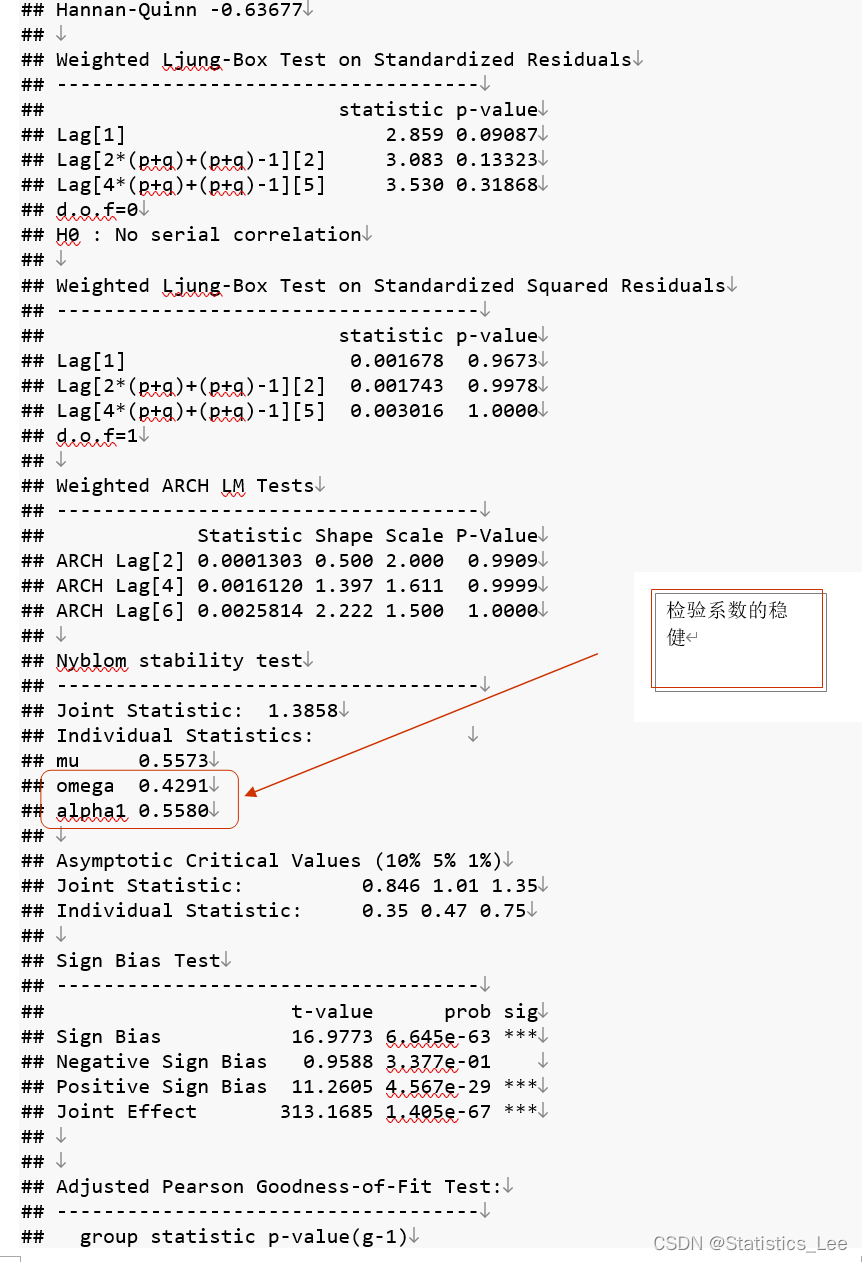

#绘制条件方差options(repr.plot.width=10, repr.plot.height=5)plot.ts(sigma(arch_model),col="blue", main = "ARCH模型的条件方差", cex.main=1) 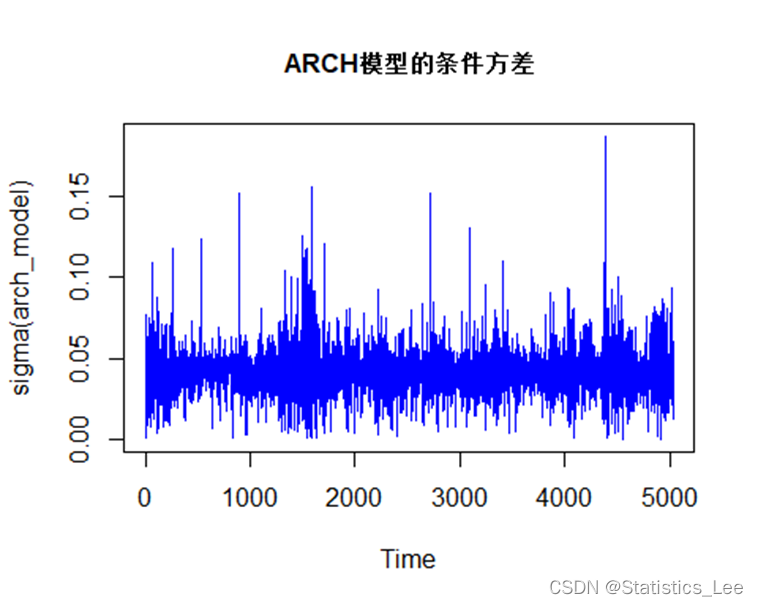
正态信息下的GARCH(1,1)
spec <- ugarchspec(variance.model=list(garchOrder=c(1,1)),mean.model=list(armaOrder=c(0,0)),distribution.model="norm")#拟合garch模型garch_model <- ugarchfit(data=return_new_data,spec=spec)garch_model
##
## *---------------------------------*
## * GARCH Model Fit *
## *---------------------------------*
##
## Conditional Variance Dynamics
## -----------------------------------
## GARCH Model : sGARCH(1,1)
## Mean Model : ARFIMA(0,0,0)
## Distribution : norm
##
## Optimal Parameters
## ------------------------------------
## Estimate Std. Error t value Pr(>|t|)
## mu 0.000647 0.000197 3.2898 0.001003
## omega 0.000011 0.000000 39.0663 0.000000
## alpha1 0.088950 0.004620 19.2528 0.000000
## beta1 0.871741 0.005908 147.5633 0.000000
##
## Robust Standard Errors:
## Estimate Std. Error t value Pr(>|t|)
## mu 0.000647 0.000200 3.2316 0.001231
## omega 0.000011 0.000001 15.2615 0.000000
## alpha1 0.088950 0.010589 8.3999 0.000000
## beta1 0.871741 0.016866 51.6873 0.000000
##
## LogLikelihood : 13901.66
##
## Information Criteria
## ------------------------------------
##
## Akaike -5.5215
## Bayes -5.5163
## Shibata -5.5215
## Hannan-Quinn -5.5197
##
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 8.041 0.004572
## Lag[2*(p+q)+(p+q)-1][2] 8.078 0.006169
## Lag[4*(p+q)+(p+q)-1][5] 9.512 0.012268
## d.o.f=0
## H0 : No serial correlation
##
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 0.09563 0.7571
## Lag[2*(p+q)+(p+q)-1][5] 0.55692 0.9486
## Lag[4*(p+q)+(p+q)-1][9] 1.04788 0.9842
## d.o.f=2
##
## Weighted ARCH LM Tests
## ------------------------------------
## Statistic Shape Scale P-Value
## ARCH Lag[3] 0.5175 0.500 2.000 0.4719
## ARCH Lag[5] 0.8480 1.440 1.667 0.7785
## ARCH Lag[7] 0.9534 2.315 1.543 0.9210
##
## Nyblom stability test
## ------------------------------------
## Joint Statistic: 25.9482
## Individual Statistics:
## mu 0.67691
## omega 3.16116
## alpha1 0.07481
## beta1 0.05598
##
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic: 1.07 1.24 1.6
## Individual Statistic: 0.35 0.47 0.75
##
## Sign Bias Test
## ------------------------------------
## t-value prob sig
## Sign Bias 0.9079 0.3640
## Negative Sign Bias 1.4981 0.1342
## Positive Sign Bias 0.1469 0.8832
## Joint Effect 2.4158 0.4907
##
##
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 237.6 9.746e-40
## 2 30 274.1 1.008e-41
## 3 40 284.6 4.477e-39
## 4 50 290.6 4.866e-36
##
##
## Elapsed time : 0.4496911
options(repr.plot.width=10, repr.plot.height=5)plot.ts(sigma(garch_model), , col="blue", main = "GARCH模型的条件方差", cex.main=1)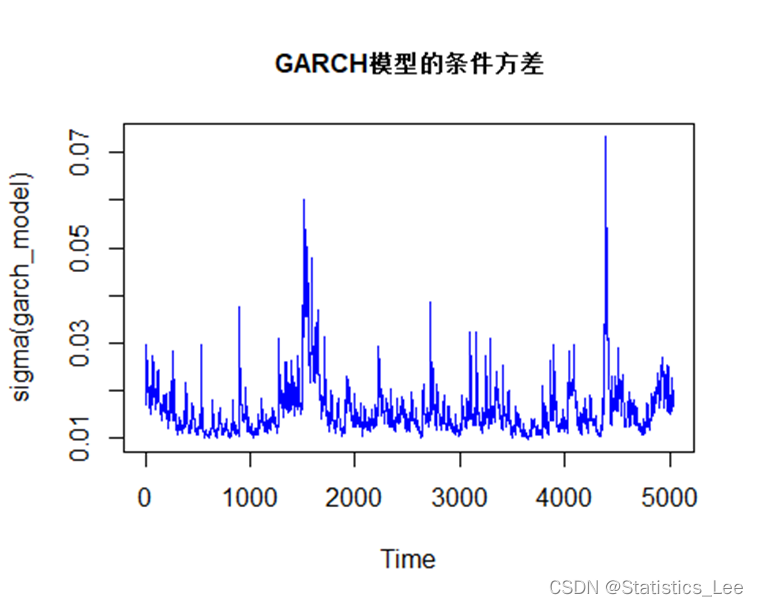
plot(garch_model,which = 9) 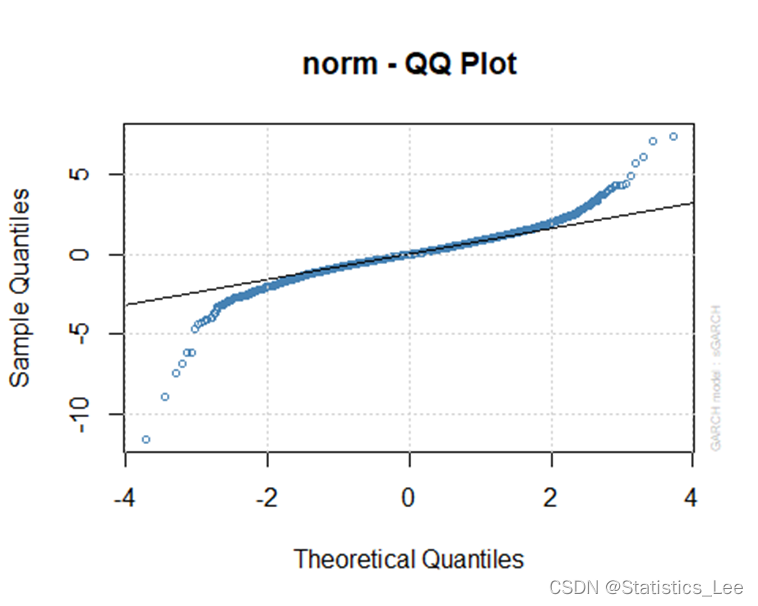
从QQ可看出,用正态信息下的ARCH(1),GARCH(1,1)估计此模型也许不大合适,接下来我们考虑非正态情况下的ARCH与GARCH估计
t分布下的ARCH和GARCH估计
spec <- ugarchspec(variance.model = list(garchOrder = c(1,0)), mean.model = list(armaOrder=c(0,0)),distribution.model="std")#拟合ARCH模型arch_model_t <- ugarchfit(data=return_new_data,spec = spec)arch_model_t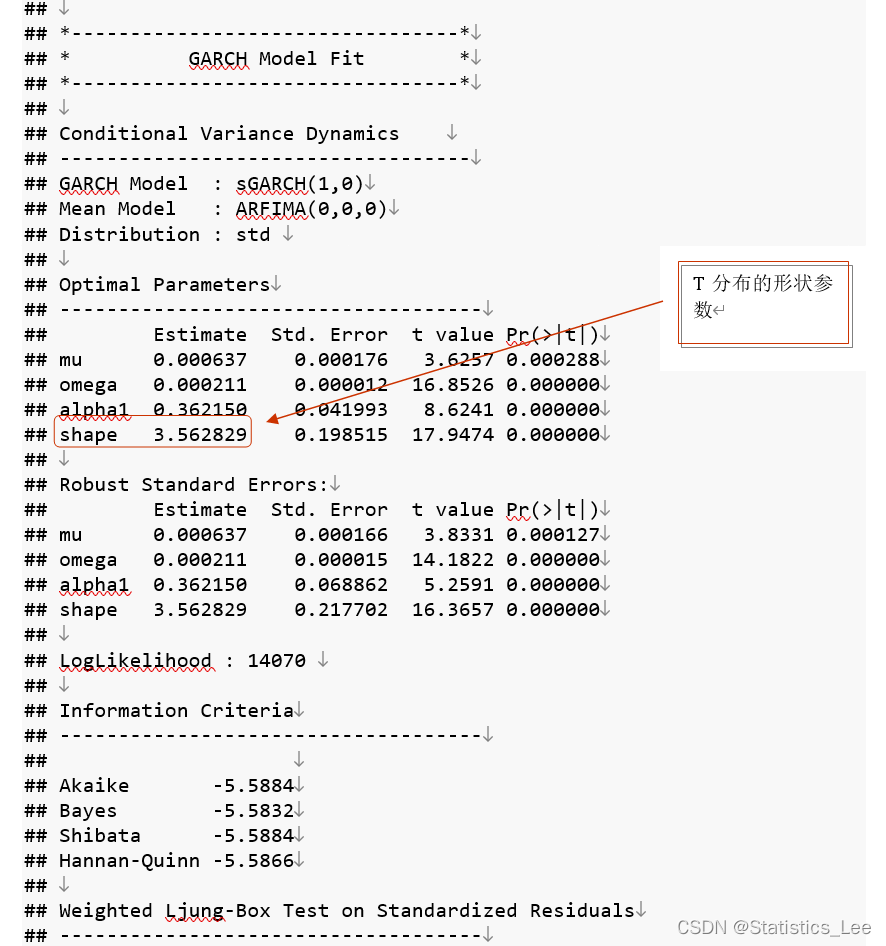
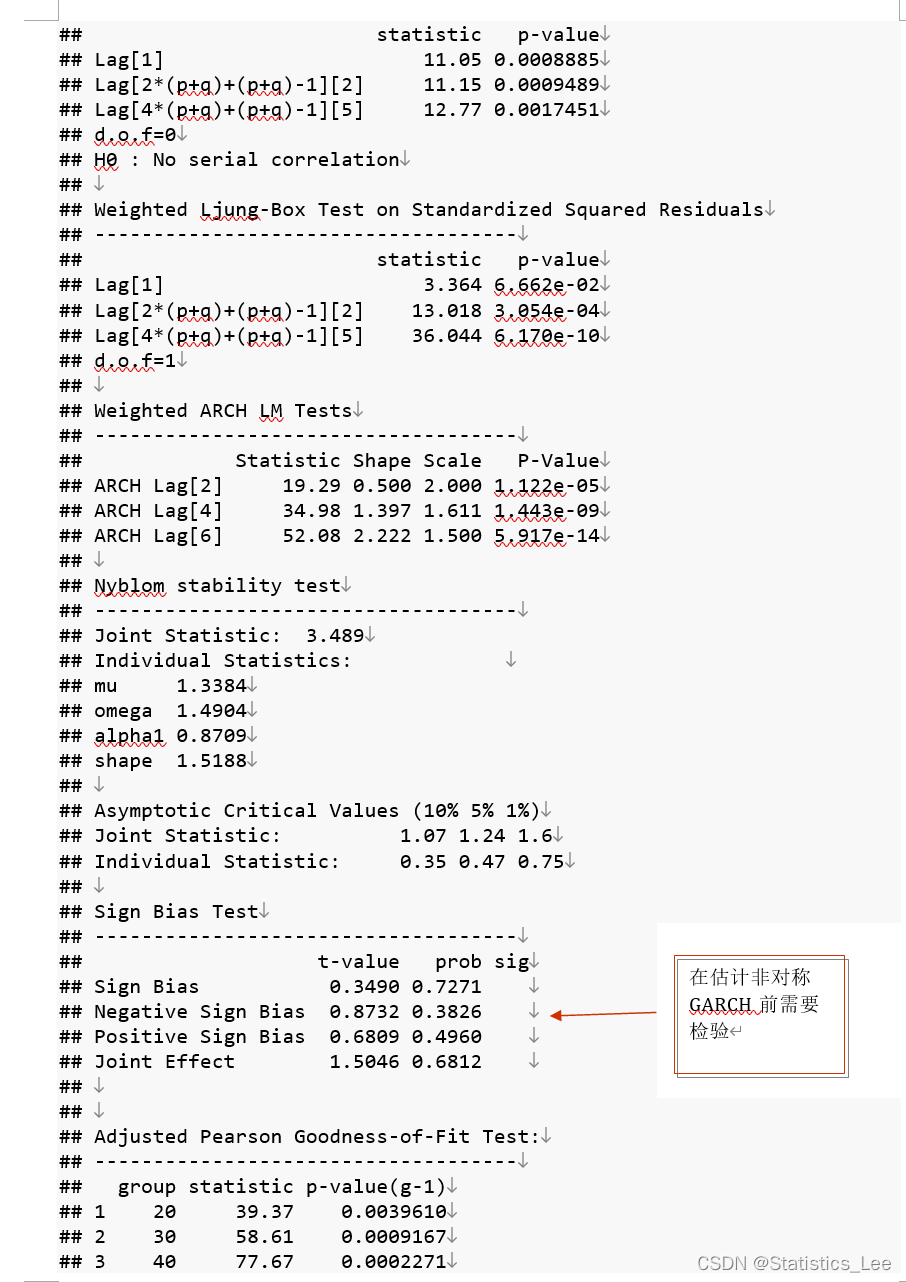
plot(garch_model_t, which=9) 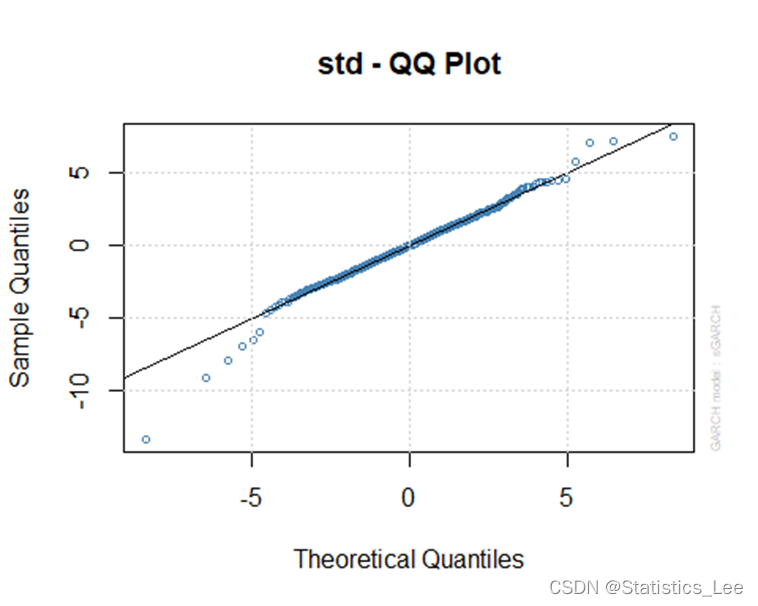
t分布情况下的Garch(1,1)的QQ图表现更好
接下来展示t分布情况下GARCH(1,1)的各个图
options(repr.plot.width=15, repr.plot.height=15)plot(garch_model_t, which= "all")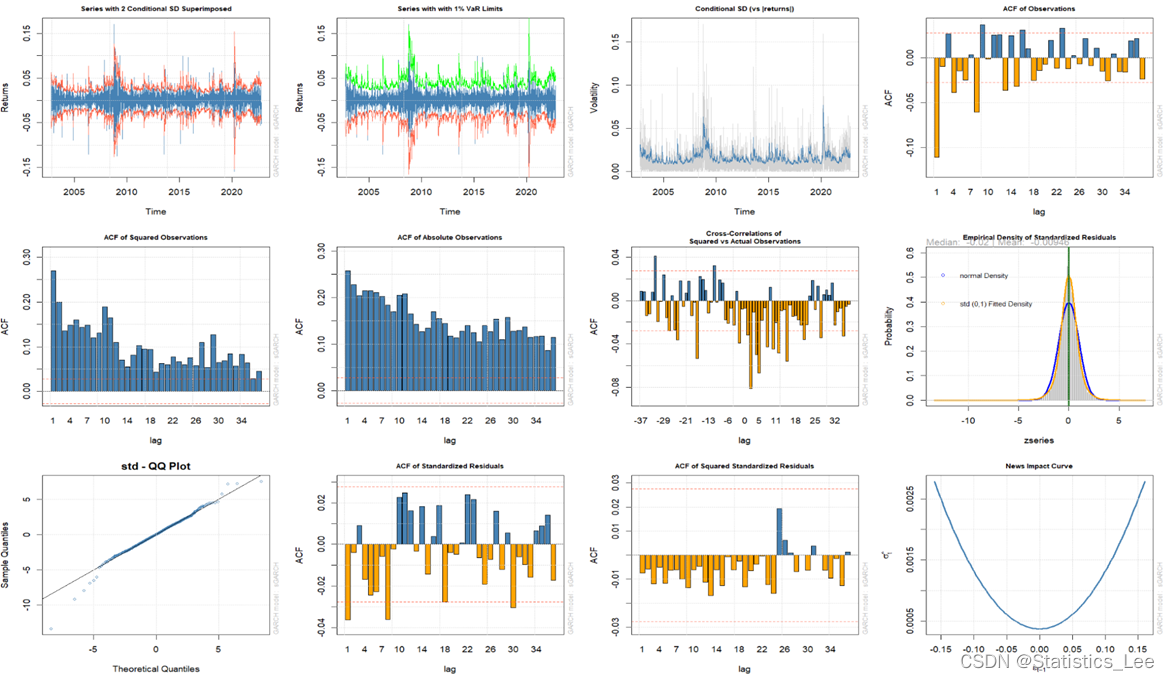
使用信息准则进行模型的选择
model.list <- list("arch(1,1)" = arch_model, "arch(1,1)-t" = arch_model_t, "garch(1,1)" = garch_model, "garch(1,1)-t" = garch_model_t)info.mat = sapply(model.list, infocriteria)rownames(info.mat) = rownames(infocriteria(garch_model))info.mat## arch(1,1) arch(1,1)-t garch(1,1) garch(1,1)-t## Akaike -0.6381349 -5.588399 -5.521518 -5.674072## Bayes -0.6342470 -5.583215 -5.516334 -5.667592## Shibata -0.6381357 -5.588401 -5.521519 -5.674074## Hannan-Quinn -0.6367727 -5.586583 -5.519702 -5.671802garch(1,1)-t在信息准则下表现最佳