数学建模系列文章:
以下是个人在准备数模国赛时候的一些模型算法和代码整理,有空会不断更新内容:
评价模型(一)层次分析法(AHP),熵权法,TOPSIS分析 及其对应 PYTHON 实现代码和例题解释
评价模型(二)主成分分析、因子分析、二者对比及其对应 PYTHON 实现代码和例题解释
优化模型(零)总述,分类,解析各类优化模型及普适做题步骤
优化模型(一)线性规划详解,以及例题,用python的Pulp库函数求解线性规划
优化模型(二)非线性规划详解,以及例题,Scipy.optimize 求解非线性规划
文章
1.1 层次分析法
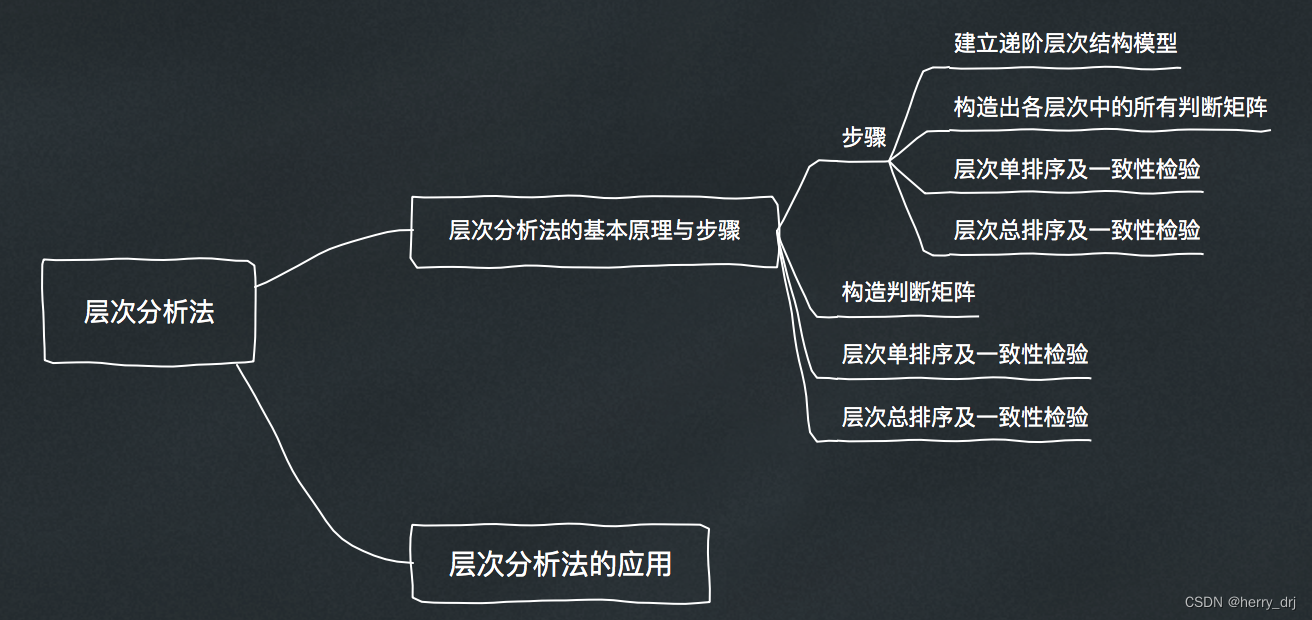
层次分析法介绍:
问题引入:
评价类模型是最基础的模型之一,往往对应着生活中一些很实际的问题。例如,高考结束了,你是选择南大还是武大呢?已知今天空气中几种污染气体的浓度,如何确定空气质量等级呢?放假想要出去旅游,有好几个备选目的地,如果只能选一个,该去哪里呢?
基本思想:
是定性与定量相结合的多准则决策、评价方法。将决策的有关元素分解成目标层、准则层和方案层(层次的来源),并通过人们的判断对决策方案的优劣进行排序,在此基础上进行定性和定量分析。它把人的思维过程层次化、数量化,并用数学为分析、决策、评价、预报和控制提供定量的依据。
基本步骤:
1. 构建层次结构模型;
2. 构建成对比较判断矩阵;
这n个指标的重要程度肯定是不一样的,我们需要定出这n个指标的权重。由于指标比较多,直接定权重难度较大,且主观因素太强,故我们采用的方法是对这些指标两两进行比较,从而在一定程度上削弱主观因素
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yVe5pTQI-1691547591221)(D:\S\typora文件夹\img\image-20230804162021988.png)]](http://zhangshiyu.com/zb_users/upload/2024/05/20240502173955171464279526940.png)
3. 一致性检验(即判断主观构建的成对比较矩阵在整体上是否有较好的一致性);
一致性检验结果要求CR值(CR=CI/RI)小于0.1,用于判断人们在构建判断矩阵时,是否存在逻辑错误,例如有ABC三个指标,我们判断A比B重要,B比C重要,因此逻辑上A肯定比C重要,但是如果在构建判断A比C时,认为C比A重要,那么就犯了逻辑错误,无法通过一致性检验。
具体方法如下:

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3VfVYavl-1691547591221)(D:\S\typora文件夹\img\image-20230804165156798.png)]](http://zhangshiyu.com/zb_users/upload/2024/05/20240502173955171464279528464.png)
求权重有三种方法,一般用第三种方法会多一些,但在实际应用中,也可以把三种方法得到的结果取平均值,得到最终的权重。
算数平均法求权重

几何平均法求权重

特征值法求权重

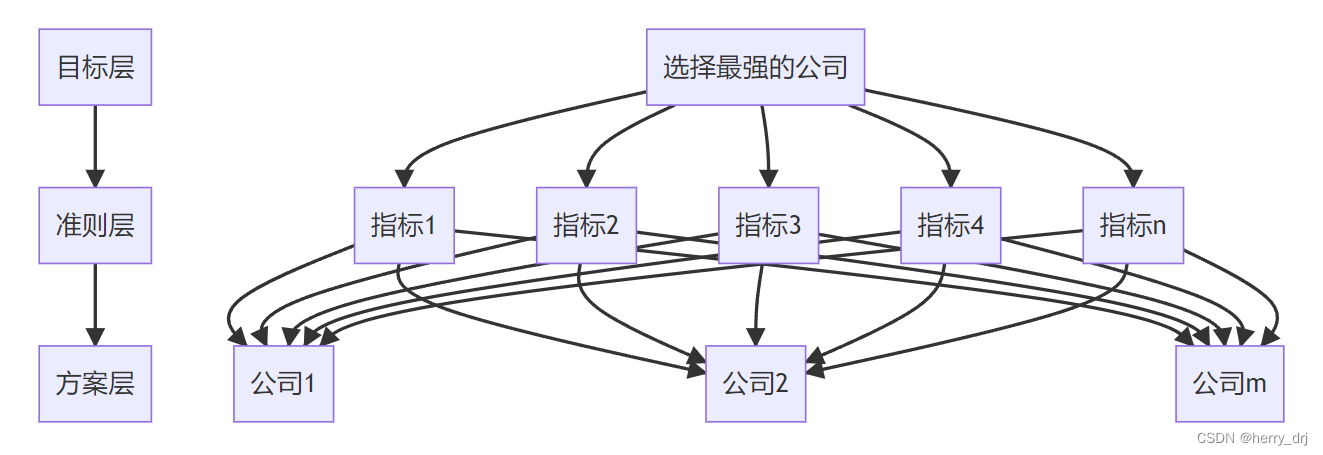
举例:高考后选择南大还是武大呢?评价的目标就是选择学校,达成目标的方案就是选择南大或者选择武大,相关的指标有 学科实力,校园景色,男女比例(指标) 等等
假设指标权重已经通过一致性检验并且计算得知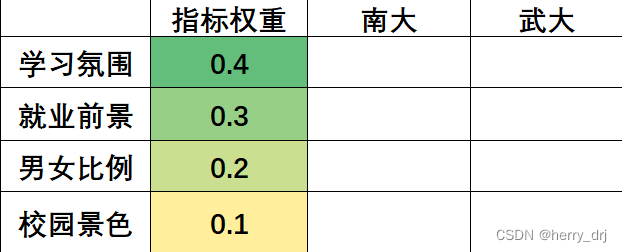
按照每个指标给南大和武大打分(打分可以是百分制的,也可以是针对每一个目标比如学习氛围、就业前景再按照层次分析法确定南大和武大的权重得分),最后再加权求和,便可以给出两个学校比较合理的得分。
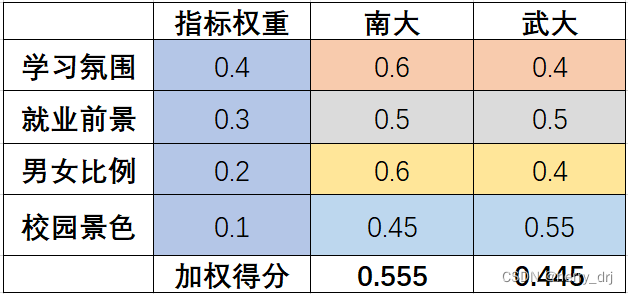
考虑到对于不同的评价问题存在不同的指标,其量纲往往是不同的,不一定都是以分数都是衡量标准。因此对于某个指标,给不同的方案进行打分时,我们依然以“权重”作为其衡量的标准,其权重之和为1即可。如上图所示,相同颜色的单元格和为1,指标权重比较好理解,给予指标以不同的权重以加权。打分也是以“权重”来衡量,南大在学习氛围方面是0.6,武大便是0.4。如果再加一个东南,那学习氛围方面可能就是0.3,0.25,0.45,其加和依然是1。当然,我们也可以将正常打分作为衡量标准,例如学习氛围分数分别为95,90。但是为了整体更方便计算,这里选择“权重”作为衡量的标准,特此说明。
优缺点:
优点:
它完全依靠主观评价做出方案的优劣排序,所需数据量少,决策花费的时间很短。从整体上看,AHP在复杂决策过程中引入定量分析,并充分利用决策者在两两比较中给出的偏好信息进行分析与决策支持,既有效地吸收了定性分析的结果,又发挥了定量分析的优势,从而使决策过程具有很强的条理性和科学性,特别适合在社会经济系统的决策分析中使用。
缺点:
用AHP进行决策主观成分很大。当决策者的判断过多地受其主观偏好影响,而产生某种对客观规律的歪曲时,AHP的结果显然就靠不住了。
适用范围:
尤其适合于人的定性判断起重要作用的、对决策结果难于直接准确计量的场合。要使AHP的决策结论尽可能符合客观规律,决策者必须对所面临的问题有比较深入和全面的认识。另外,当遇到因素众多,规模较大的评价问题时,该模型容易出现问题,它要求评价者对问题的本质、包含的要素及其相互之间的逻辑关系能掌握得十分透彻,否则评价结果就不可靠和准确。
改进方法:
(1) 成对比较矩阵可以采用德尔菲法获得。
(2) 如果评价指标个数过多(一般超过9个),利用层次分析法所得到的权重就有一定的偏差,继而组合评价模型的结果就不再可靠。可以根据评价对象的实际情况和特点,利用一定的方法,将各原始指标分层和归类,使得每层各类中的指标数少于9个。
补充:
德尔菲法,也称专家调查法,1946年由美国兰德公司创始实行,其本质是一种反馈匿名函询法,其大致流程是在对所要预测的问题征得专家的意见之后,进行整理、归纳、统计,在匿名反馈给各专家,再次征求意见,再集中,再反馈,直至得到一致的意见。在评价中目的:确立评价指标。
对评价类问题建模,往往需要考虑三个方面:
评价的目标是什么?达成目标的方案有哪些?评价的指标/准则是什么?PYTHON代码:
import numpy as np # 导入所需包并将其命名为npA = [[1,1,4,1/3,3], [1,1,4,1/3,3], [1/2,1/4,1,1/3,1/2], [3,3,3,1,3], [1/3,1/3,2,1/3,1]]def ConsisTest(X): # 函数接收一个如上述A似的矩阵 # 计算权重 # 方法一:算术平均法 ## 第一步:将判断矩阵按照列归一化(每个元素除以其所在列的和) X = np.array(X) # 将X转换为np.array对象 sum_X = X.sum(axis=0) # 计算X每列的和 (n, n) = X.shape # X为方阵,行和列相同,所以用一个n来接收 sum_X = np.tile(sum_X, (n, 1)) # 将和向量重复n行组成新的矩阵 stand_X = X / sum_X # 标准化X(X中每个元素除以其所在列的和) ## 第二步:将归一化矩阵每一行求和 sum_row = stand_X.sum(axis=1) ## 第三步:将相加后得到的向量中每个元素除以n即可得到权重向量 print("算数平均法求权重的结果为:") print(sum_row / n) # 方法二:特征值法 ## 第一步:找出矩阵X的最大特征值以及其对应的特征向量 V, E = np.linalg.eig(X) # V是特征值,E是特征值对应的特征向量 max_value = np.max(V) # 最大特征值 # print("最大特征值是:",max_value) max_v_index = np.argmax(V) # 返回最大特征值所在位置 max_eiv = E[:, max_v_index] # 最大特征值对应的特征向量 ## 第二步:对求出的特征向量进行归一化处理即可得到权重 stand_eiv = max_eiv / max_eiv.sum() print("特征值法求权重的结果为:") print(stand_eiv) print("———————————————————————————————") # 一致性检验 ## 第一步:计算一致性指标CI CI = (max_value - n) / (n - 1) ## 第二步:查找对应的平均随机一致性指标RI RI = np.array([15, 0, 0, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41, 1.46, 1.49, 1.52, 1.54, 1.56, 1.58, 1.59]) ## 第三步:计算一致性比例CR CR = CI / RI[n] if CR < 0.1: print("CR=", CR, ",小于0.1,通过一致性检验") else: print("CR=", CR, ",大于等于0.1,没有通过一致性检验,请修改判断矩阵") return NoneConsisTest(A)论文解读:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-t81i1naI-1691547591222)(D:\S\typora文件夹\img\image-20230806224641292.png)]](http://zhangshiyu.com/zb_users/upload/2024/05/20240502173956171464279637174.png)
1.2 熵权法
熵权法介绍:
层次分析法的权重带有很重的主观色彩,而为了使权重更加客观,我们利用原始数据中的某些特性来确定权重。一列数据方差越小,指标的变异程度越小,所反映的信息量也越少,那么此时其权重就应该越低。而一列数据所反映的信息量越少,其信息熵就越大。所以指标的信息熵就是这样一个具有优良性质的特性。而且信息熵越大,权重就越低。(客观 = 数据本身就可以告诉我们权重)
熵权法只是一个确定权重的方法,一般和别的方法(如TOPSIS法)一起使用。
基本步骤:
数据标准化由于每一列数据可能代表不同类别,不同单位的信息,所以为了方便比较,我们需要对数据进行标准化处理。

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zkAjRf5L-1691547591223)(D:\S\typora文件夹\img\image-20230806193409827.png)]](http://zhangshiyu.com/zb_users/upload/2024/05/20240502173956171464279664447.png)

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RhnrEhgp-1691547591223)(D:\S\typora文件夹\img\image-20230806193912914.png)]](http://zhangshiyu.com/zb_users/upload/2024/05/20240502173956171464279656612.png)
PYTHON代码:
import pandas as pdimport numpy as npimport re#定义文件读取方法def read_data(file): file_path=file raw_data = pd.read_excel(file_path, header=0) #print(raw_data) return raw_data #定义数据正向化、标准化方法def data_normalization(data): data_nor=data.copy() columns_name=data_nor.columns.values for i in range((len(columns_name)-1)): name=columns_name[i+1] #print(name) #正向指标直接标准化 if ('Positive' in name)==True: max=data_nor[columns_name[i+1]].max() min=data_nor[columns_name[i+1]].min() data_nor[columns_name[i+1]]=(data_nor[columns_name[i+1]]-min)/(max-min) #print(data_nor[columns_name[i+1]]) #负向指标先正向化、在标准化 if ('Negative' in name)==True: max0=data_nor[columns_name[i+1]].max() data_nor[columns_name[i+1]]=(max0-data_nor[columns_name[i+1]])#正向化 max=data_nor[columns_name[i+1]].max() min=data_nor[columns_name[i+1]].min() data_nor[columns_name[i+1]]=(data_nor[columns_name[i+1]]-min)/(max-min)#标准化 #print(data_nor[columns_name[i+1]]) #适度指标先正向化、在标准化 if ('Moderate' in name)==True: try: val_range= re.search(r'.*[\((](.*),(.*)[\))]',name) val_down= float(val_range.group(1)) val_up= float(val_range.group(2)) val_op=(val_up+val_down)/2 except: val_range= re.search(r'.*[\((](.*)[\))]',name) val_op= float(val_range.group(1)) #print(val_op) data_nor[columns_name[i + 1]] = 1-(abs(data_nor[columns_name[i + 1]]-val_op)/(abs(data_nor[columns_name[i + 1]]-val_op).max())) #正向化 max=data_nor[columns_name[i+1]].max() min=data_nor[columns_name[i+1]].min() data_nor[columns_name[i+1]]=(data_nor[columns_name[i+1]]-min)/(max-min)#标准化 #print(data_nor[columns_name[i+1]]) #print(data_nor) return data_nor #定义计算熵权方法def entropy_weight(data_nor): columns_name=data_nor.columns.values n=data_nor.shape[0] E=[] for i in columns_name[1:]: #计算信息熵 #print(i) data_nor[i]=data_nor[i]/sum(data_nor[i]) data_nor[i]=data_nor[i]*np.log(data_nor[i]) data_nor[i]=data_nor[i].where(data_nor[i].notnull(),0) #print(data_nor[i]) Ei=(-1)/(np.log(n))*sum(data_nor[i]) E.append(Ei) #print(E) #计算权重 W=[] for i in E: wi=(1-i)/((len(columns_name)-1)-sum(E)) W.append(wi) #print(W) return W #计算得分def entropy_score(data,w): data_s=data.copy() columns_name=data_s.columns.values for i in range((len(columns_name)-1)): name=columns_name[i+1] data_s[name]=data_s[name]*w[i] return data_s file='data.xls'#声明数据文件地址data=read_data(file)#读取数据文件data_nor=data_normalization(data)#数据标准化、正向化,生成标准化后的数据data_norW=entropy_weight(data_nor)#计算熵权权重data_s=entropy_score(data,W)#计算赋权后的得分,使用原数据计算data_nor_s=entropy_score(data_nor,W) W.insert(0,'熵权法权重')#将结果保存为csvW0=pd.DataFrame(W).Tdata_s.to_csv('熵权法得分结果(原始数据).csv',index=0)W0.to_csv('熵权法得分结果(原始数据).csv', mode='a', header=False,index=0)data_nor_s.to_csv('熵权法得分结果(标准化数据).csv',index=0)W0.to_csv('熵权法得分结果(标准化数据).csv', mode='a', header=False,index=0)1.3 TOPSIS优劣解距离法
TOPSIS介绍:
TOPSIS 法(Technique for Order Preference by Similarity to Ideal Solution)
可翻译为逼近理想解排序法,国内常简称为优劣解距离法
层次分析法和熵权法都是得到权重的方法,而得到权重之后直接通过加权平均来计算每一家公司的得分,对于数据没有充分地利用。而TOPSIS法则充分利用原始数据的信息,其结果能精确地反映各评价方案之间的差距。
直观理解,就是在所有指标中选出最大值(最小值),组成一个最优方案(最劣方案)。距离最优方案越近、离最劣方案越远的那个方案就是最优方案。
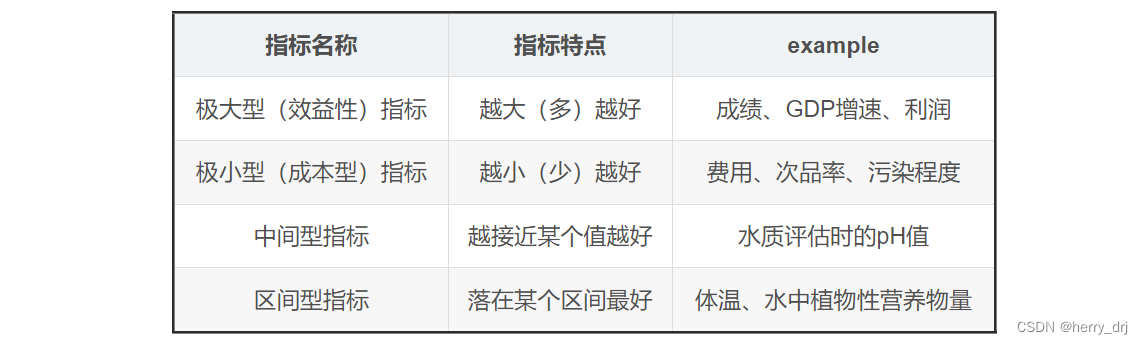
极大型指标: 越大越高越好,又称效益型指标,一般是好的
极小型指标: 越小越少越好,又称成本型指标,一般是不好的
基本步骤:
前期数据处理: 指标正向化:极小型指标转化为极大型指标 max{Xi}-Xi为了消去不同指标量纲的影响,需要对已经正向化的矩阵进行标准化处理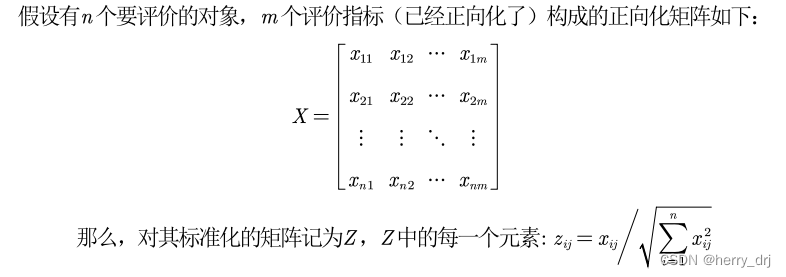
定义最大值和最小值:
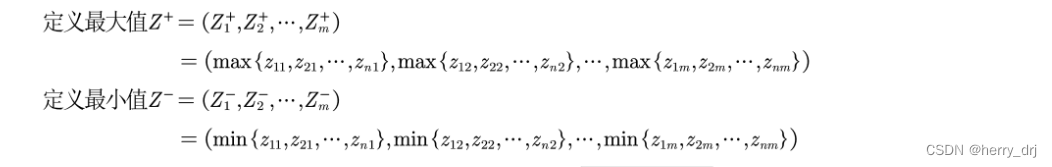
定义距离:
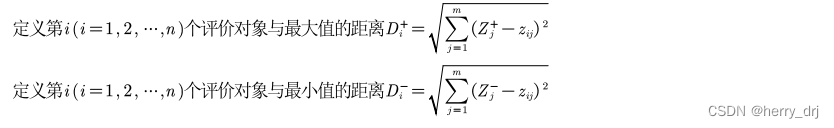
计算得分并归一化:

补充几点说明:
权值:
首先注意公式里面的权值Wi,这个是十分重要的权值的来源可以由层次分析法求得。不过一般是熵权法,因为层次分析法主观性太强归一化和标准化的区别
先说是什么,再说为什么,再说应用。
归一化:就是将训练集中某一列数值特征(假设是第i列)的值缩放到0和1 或者 -1和1 之间。方法如下所示:
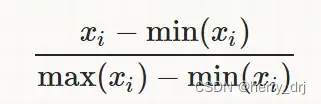
标准化:就是将训练集中某一列数值特征(假设是第i列)的值缩放成均值为0,方差为1的状态。(也有矩阵的标准化,每个向量的值除以总长度,比如TOPSIS的标准化方法)如下所示:
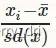
进一步明确含义: 归一化和标准化的相同点都是对某个特征(column 纵向)进行缩放(scaling)而不是对某个样本的特征向量(row 横向)进行缩放。在机器学习中对特征向量进行横向缩放是毫无意义的,但是在NLP中,是会进行横向缩放的,因为句子的长度不确定,特征数量不一定对齐,这也就是自然语言处理中常用的LayerNormalization(层标准化)
联系和作用
本质上都是进行特征提取,数据都通过先平移(分子相减)后缩放(分母)进行进行提取;都是为了缩小范围.便于后续的数据处理.
加快梯度下降,损失函数收敛;—速度上
提升模型精度–也就是分类准确率.(消除不同量纲,便于综合指标评价,提高分类准确率)—质量上
防止梯度爆炸(消除因为数据输入差距(1和2000)过大,而带来的输出差距过大(0.8,999),进而在 反向传播的过程当中,导致梯度过大(因为反向传播的过程当中进行梯度计算,会使用的之前对应层的输入x),从而形成梯度爆炸)—稳定性上
标准化和归一化的对比分析:
归一化: 主要应用与没有距离计算的地方(丢失分布与距离,保留权值信息)— 奇异数据,小数据场景
标准化:主要应用于不关乎权重的地方(保留分布与距离,丢失权值信息,用在开始)—-需要距离来度量相似性,有异常值和噪声
eg:
比如三个样本,某个特征的值为1,2,10000,假设10000这个值是异常值,用归一化的方法后,正常的1,2就会被“挤”到一起去。如果不幸的是1和2的分类标签还是相反的,那么,当我们用梯度下降来做分类模型训练时,模型会需要更长的时间收敛,因为将样本分开需要更大的努力!而标准化在这方面就做得很好,至少它不会将样本“挤到一起”。
哪些算法需要归一化/标准化:
有时候,我们必须要特征在0到1之间,此时就只能用归一化 (熵权法第一步骤) 。涉及或隐含距离计算的算法分类、聚类,比如K-means(标准化)、KNN(标准化)、PCA(标准化)、SVM(归一化)等,一般需要进行归一化/标准化。
梯度下降算法,梯度下降的收敛速度取决于:参数的初始位置到local minima的距离,以及学习率η的大小,其实还是距离的计算。
采用sigmoid等有饱和区的激活函数,如果输入分布范围很广,参数初始化时没有适配好,很容易直接陷入饱和区,导致梯度消失,所以才会出现各种BN,LN等算法。
如果数据不为稳定,存在极端的最大最小值,不要用归一化。可以使用标准化。如上例。
哪些算法不需要归一化/标准化:
0/1取值的特征,如果归一化会破坏稀疏性;与距离计算无关的概率模型不需要,比如Naive Bayes;与距离计算无关的基于树的模型,比如决策树、随机森林等,树中节点的选择只关注当前特征在哪里切分对分类更好,即只在意特征内部的相对大小,而与特征间的相对大小无关。树模型并不关心特征的具体取值,只关心特征取值的分布最常见的四种指标&&转换为极大型的方法:


总结TOPSIS:
TOPSIS可以用以下几个式子总结:
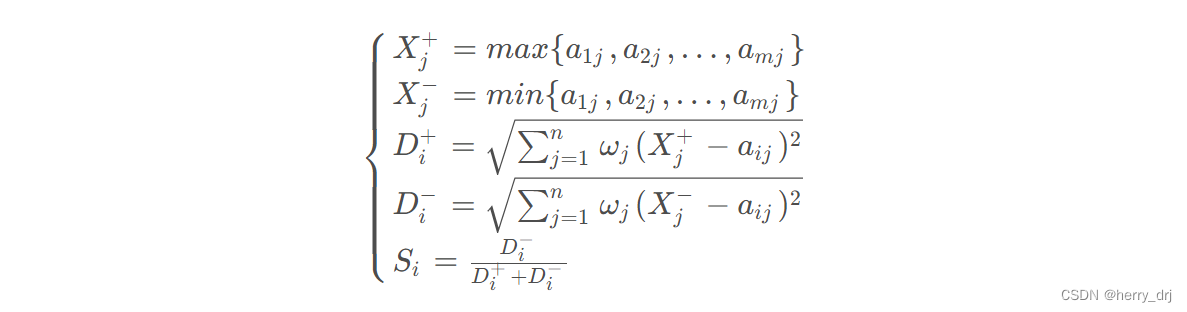
TOPSIS法的基本过程为先将原始数据矩阵统一指标类型(一般正向化处理) 得到正向化的矩阵,再对正向化矩阵进行标准化处理以消除各指标量纲的影响,并找到有限方案中的最优方案和最劣方案,然后分别计算各评价对象与最优方案和最劣方案间的距离,获得各评价对象与最优方案的相对接近程度,以此作为评价优劣的依据。该方法对数据分布及样本含量没有严格限制,数据计算简单易行。
个人理解:找到所有因子的最优值和最劣值组成一个多维最优向量和最劣向量,然后计算每一个样本举例最优值的距离和最劣值的向量,越远离最差向量的样本 排名(分数)越高。
论文解读:

例题:
这条比较典型,里面有极大型,极小型,中间型,区间型指标。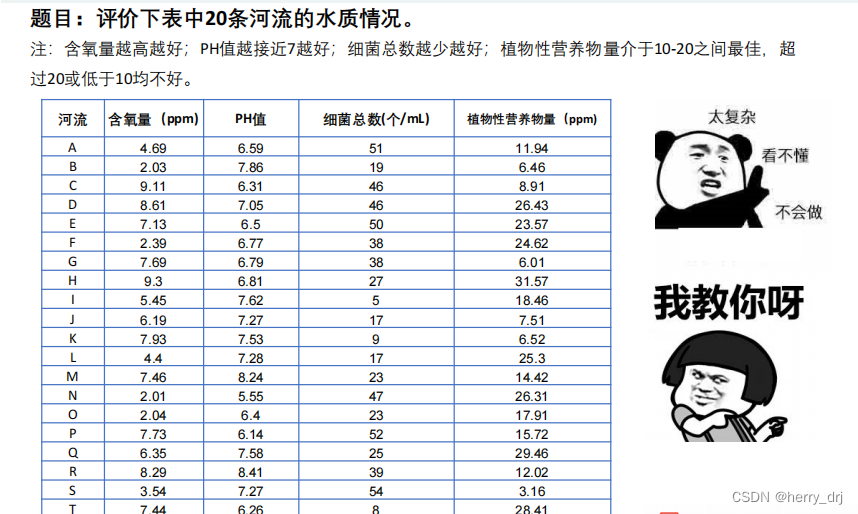
PYTHON代码:
# 导入分析库import pandas as pdimport numpy as np##导入数据df = pd.read_excel(r'D:\S\20条河流的水质情况数据.xls')print(df.head(5)) # 查看头5条数据# 极小型指标 -> 极大型指标def Mintomax(datas): return np.max(datas) - datasdf['细菌总数(个/mL)'] = Mintomax(df['细菌总数(个/mL)']) # 极小型指标 -> 极大型指标df.head() # 查看# 中间型指标 -> 极大型指标def Midtomax(datas, x_best): temp_datas = datas - x_best M = np.max(abs(temp_datas)) answer_datas = 1 - abs(datas - x_best) / M return answer_datasdf['PH值'] = Midtomax(df['PH值'], 7) # 中间型指标 -> 极大型指标 7为最佳值# 区间型指标 -> 极大型指标def Intertomax(datas, x_min, x_max): M = max(x_min - np.min(datas), np.max(datas) - x_max) answer_list = [] for i in datas: if (i < x_min): answer_list.append(1 - (x_min - i) / M) elif (i > x_max): answer_list.append(1 - (i - x_max) / M) else: answer_list.append(1) return np.array(answer_list)df['植物性营养物量(ppm)'] = Intertomax(df['植物性营养物量(ppm)'], 10, 20) # 区间型指标 -> 极大型指标# 正向化矩阵标准化(去除量纲影响)def Standard(datas): k = np.power(np.sum(pow(datas, 2), axis=0), 0.5) for i in range(len(k)): datas[:, i] = datas[:, i] / k[i] return dataslabel_need = df.keys()[1:]data = df[label_need].values # 刨除变量名后的数据值sta_data = Standard(data) # 正向化矩阵标准化(去除量纲影响)# 正向化和标准化print(sta_data)# 10为下界,20为上界# 计算得分并归一化def Score(sta_data): z_max = np.amax(sta_data, axis=0) z_min = np.amin(sta_data, axis=0) # 计算每一个样本点与最大值的距离 tmpmaxdist = np.power(np.sum(np.power((z_max - sta_data), 2), axis=1), 0.5) tmpmindist = np.power(np.sum(np.power((z_min - sta_data), 2), axis=1), 0.5) score = tmpmindist / (tmpmindist + tmpmaxdist) score = score / np.sum(score) # 归一化处理 return scoresco = Score(sta_data) # 计算得分print(sco)1.4 参考资料:
数学建模笔记——评价类模型(一)
数学建模之评价类问题
AHP代码
层次分析法,实例例子
PYthon实现熵权
TOPSIS法——利用原始数据进行综合评价
归一化和标准化
机器学习面试之归一化与标准化
机器学习 数据特征 标准化和归一化
标准化和归一化,请勿混为一谈,透彻理解数据变换
数学建模之评价类问题