这是hnu人工智能的第三次实验,本人在做这次实验时看网上尽管有零零散散的相关帖子,但却没有一个系统的整合分析,因此头脑一热写了这篇文章,当然是借鉴了网上的诸多大佬帖。由于本人的实验当时是使用word完成的,因此相关代码分析都是图片展示,完整的代码在最后附上,需要的同学自取,此帖仅为本人学习总结,如有侵权,联系速删.
参考:
程子的小段_机器学习 --- 朴素贝叶斯分类器
A橙_人工智能-实验三
实验三:分类算法实验
一.实验目的
掌握分类算法的算法思想:朴素贝叶斯算法,决策树算法,人工神经网络,支持向量机;编写朴素贝叶斯算法进行分类操作。二、实验内容
第1关:条件概率
实验原理条件概率:设A,B是两个事件,且P(A)>0,称P(B|A)=P(AB)/P(A)为在事件A发生的条件下,事件B发生的条件概率。(其中P(AB)表示事件A和事件B同时发生的概率)
2、实验内容
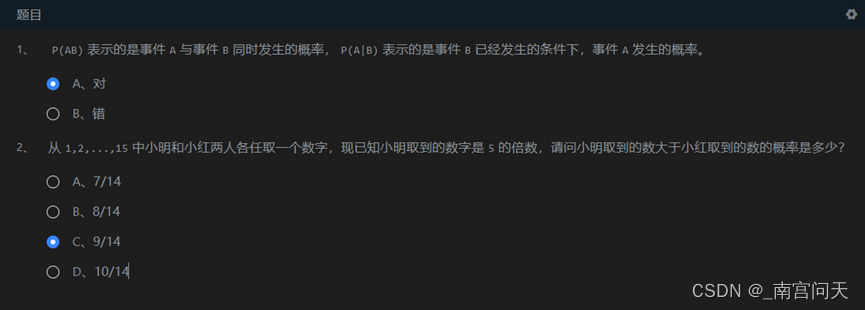
第一题由概念易知其正确。
第二题答案为1/3 *(4/14+9/14+14/14)=9/14,因为小明已知取到的数字为5的倍数,可能的情况为5,10,15三种情况,对于每种情况其取到的数字大于小红的概率分别为4/14,9/14,1,因此把每种情况的获胜概率✖对于情况发生的概率1/3,在进行累加即可。
评测结果
第2关:贝叶斯公式
1、实验原理
全概率公式
当为了达到某种目的,但是达到目的有很多种方式,如果想知道通过所有方式能够达到目的的概率是多少的话,就需要用到全概率公式。全概率公式的定义如下:
若事件B1,B2,...,Bn两两互不相容,并且其概率和为1。那么对于任意一个事件C都满足:

贝叶斯公式
当已知引发事件发生的各种原因的概率,想要算该事件发生的概率时,我们可以用全概率公式。但如果现在反过来,已知事件已经发生了,但想要计算引发该事件的各种原因的概率时,我们就需要用到贝叶斯公式了。
贝叶斯公式定义如下,其中A表示已经发生的事件,Bi为导致事件A发生的第i个原因:
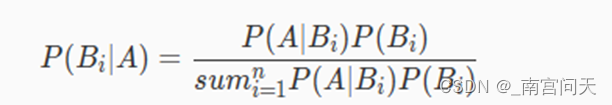
贝叶斯公式看起来比较复杂,其实非常简单,分子部分是乘法定理,分母部分是全概率公式(分母等于P(A))。
如果我们对贝叶斯公式进行一个简单的数学变换(两边同时乘以分母,再两边同时除以P(Bi))。就能够得到如下公式:
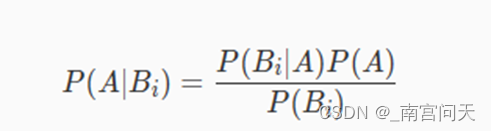
这个公式是朴素贝叶斯分类算法的核心数学公式
2、实验内容

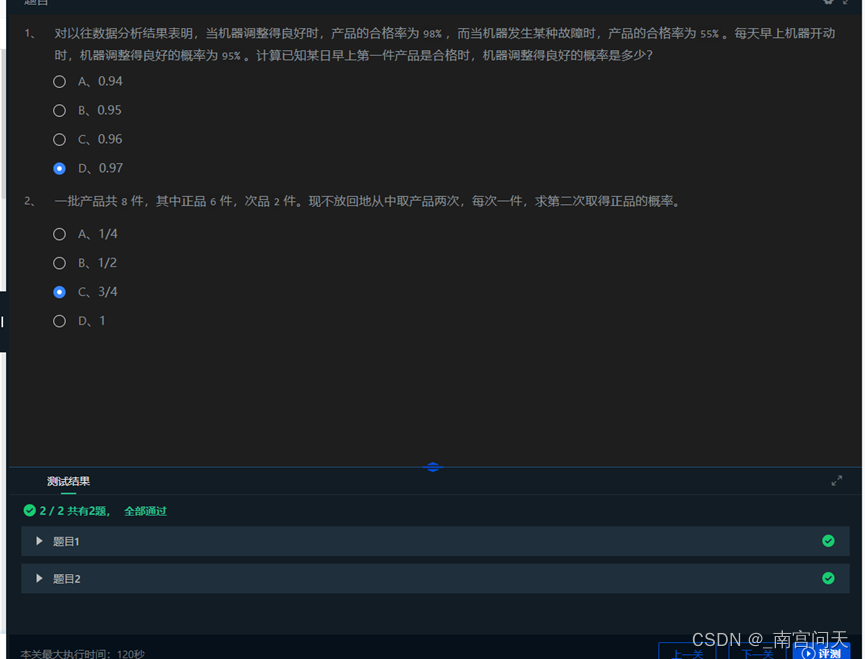
第一题:
将事件机器调整得良好定义为A1,机器发生某种故障为A2,产品是合格为B。
则已知P(A1), P(B|A1), P(B|A2),求P(A1|B)。
由贝叶斯公式易得:P(A1|B)= (P(A1)* P(B|A1))/ P(B)
P(B)= P(B|A1)* P(A1)+ P(A2)*P(B|A2)
解得P(A1|B)=0.97
第二题:
该题第一次取出的产品会影响第二次为正品的概率,因此需要分情况讨论:
第一次取出的是正品则P1=6/8*5/7=30/56第一次取出的是次品则P2=2/8*6/7=12/56∴P=P1+P2=42/56=3/4
评测结果
第3关:朴素贝叶斯分类算法流程
实验原理 朴素贝叶斯分类算法的预测思想会根据以往的经验计算出待预测数据分别为所有类别的概率,然后挑选其中概率最高的类别作为分类结果。
相关知识
为了完成本关任务,你需要掌握:
朴素贝叶斯分类算法的训练流程;朴素贝叶斯分类算法的预测流程。
模型训练的过程相当于学习P(Ai|B),其中B是特定的类别,Ai是特征。计算该概率时,假设各个特征之间互不影响,每个特征都是条件独立的。这个假设就是条件独立性假设,可以简化朴素贝叶斯方法,但可能牺牲一定的分类准确性。
模型预测的过程就是根据贝叶斯公式求P(B|Ai)的概率,即在有各个特征的条件下,预测输入属于哪一个分类的概率,属于哪一个分类的概率最大,就预测输入样本的类别是哪一类。根据贝叶斯公式,P(B|Ai)被转换为:
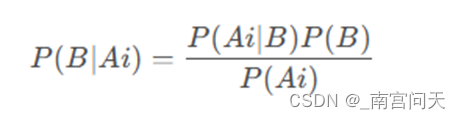
由于对于每个类别,计算公式都有分母P(Ai),因此只需要计算分子并比较大小就可以了,按照条件独立性假设,转换为:
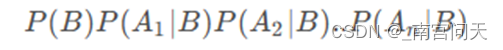
而P(Ai|B)就是模型训练时计算得到的条件概率。
2、实验内容
任务描述
本关任务:填写python代码,完成fit与predict函数,分别实现模型的训练与预测。
编程要求
根据提示,完成fit与predict函数,分别实现模型的训练与预测。(PS:在fit函数中需要将预测时需要的概率保存到self.label_prob和self.condition_prob这两个变量中)
其中fit函数参数解释如下:
feature:训练集数据,类型为ndarray;label:训练集标签,类型为ndarray;return:无返回。predict函数参数解释如下:
feature:测试数据集所有特征组成的ndarray。(PS:feature中有多条数据);return:模型预测的结果。(**PS:feature中有多少条数据,就需要返回长度为多少的list或者ndarry**)。测试说明
部分训练数据如下**(PS:数据以ndarray的方式存储,不包含表头。其中颜色这一列用1表示绿色,2表示黄色;声音这一列用1表示清脆,2表示浑厚。纹理这一列用1表示清晰,2表示模糊,3表示一般)**:
| 颜色 | 声音 | 纹理 | 是否为好瓜 |
| 2 | 1 | 1 | 1 |
| 1 | 2 | 2 | 0 |
| 2 | 2 | 2 | 1 |
| 2 | 1 | 2 | 1 |
| 1 | 2 | 3 | 1 |
| 2 | 1 | 1 | 0 |
只需完成fit与predict函数即可,程序内部会调用您所完成的fit函数构建模型并调用predict函数来对数据进行预测。预测的准确率高于0.8视为过关。
1、fit函数
朴素贝叶斯算法
假设A表示类别,B,C,D表示三个特征。根据朴素贝叶斯算法的原理,所求概率为:
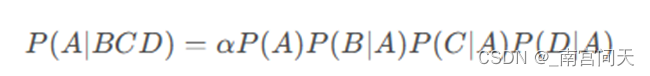
代码补全
首先了解一下朴素贝叶斯算法使用的条件概率计算结果存储结构

计算各个类别在训练样本中出现了多少个
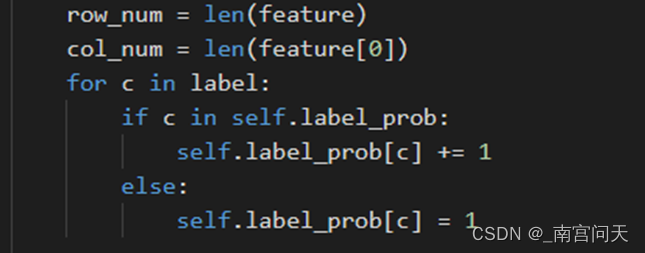
计算各个类别出现的概率及初始化两个类别下,保存特征取值概率的字典

遍历所有样本的特征,并进行每个特征取值的计数:

最后对每个样本特征除以每个类别的样本数量,得到条件概率:
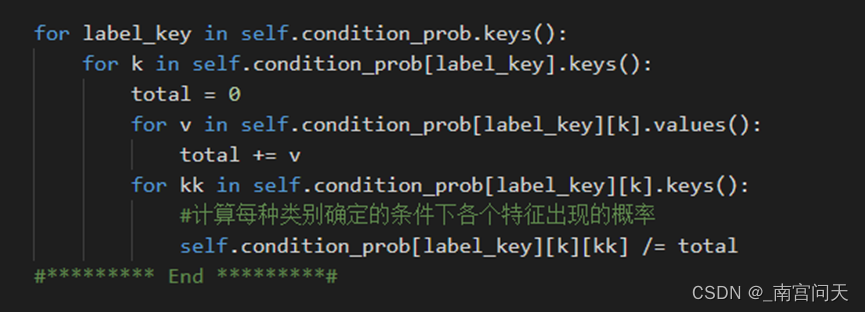
预测的过程只需要按照贝叶斯公式进行计算,由于分类只有两种(好/坏),只需要分别计算:
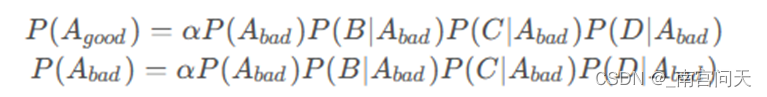
代码补全
取出每条测试数据,对每条测试数据判断其类别,首先把两个类别概率和相应特征概率进行相乘,求出相应特征产生两种类别的概率分别是多少,最后调用argmax函数求概率最大的类别,并返回对应的类别key,存储到列表result中,最后return result即可。
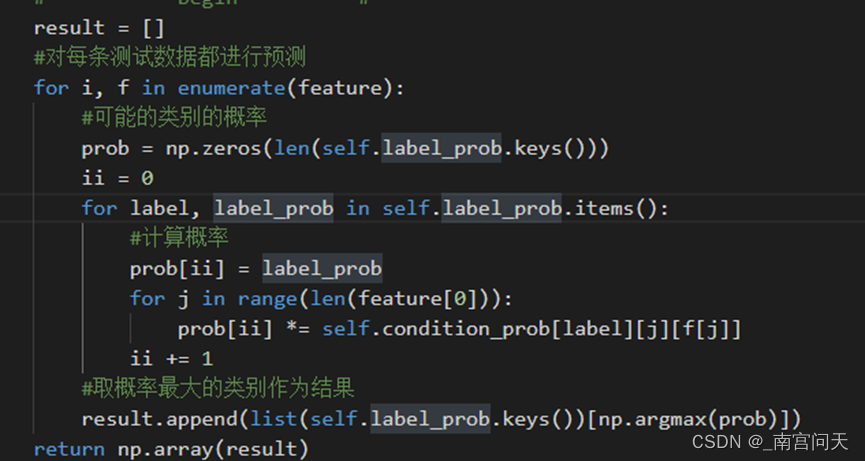
评测结果
第4关:拉普拉斯平滑
如果样本不够多,可能存在某些分类不存在特定特征,这样在利用朴素贝叶斯算法进行分类时,如果出现了这个特征,预测就不合理了。如下例:
| 编号 | 颜色 | 声音 | 纹理 | 是否为好瓜 |
| 1 | 绿 | 清脆 | 清晰 | 是 |
| 2 | 黄 | 浑厚 | 清晰 | 否 |
| 3 | 绿 | 浑厚 | 模糊 | 是 |
| 4 | 绿 | 清脆 | 清晰 | 是 |
| 5 | 黄 | 浑厚 | 模糊 | 是 |
| 6 | 绿 | 清脆 | 清晰 | 否 |
坏瓜类别中,没有纹理特征为模糊的样本,则P(模糊|坏瓜)的概率为0,如果预测的样本中出现了纹理特征为模糊,计算出的概率中,是坏瓜的概率就是0。为此要进行平滑处理,最常用的方法是拉普拉斯平滑。
拉普拉斯平滑指的是,假设N表示训练数据集总共有多少种类别,Ni表示训练数据集中第i列总共有多少种取值。则训练过程中在算类别的概率时分子加1,分母加N,算条件概率时分子加1,分母加Ni。
即P(Ai)修正为:

而P(Bj|Ai)修正为:

修正后的概率和条件概率不会为0,避免了上述不合理的情况。
根据拉普拉斯平滑原理,计算类别概率的过程修改为:
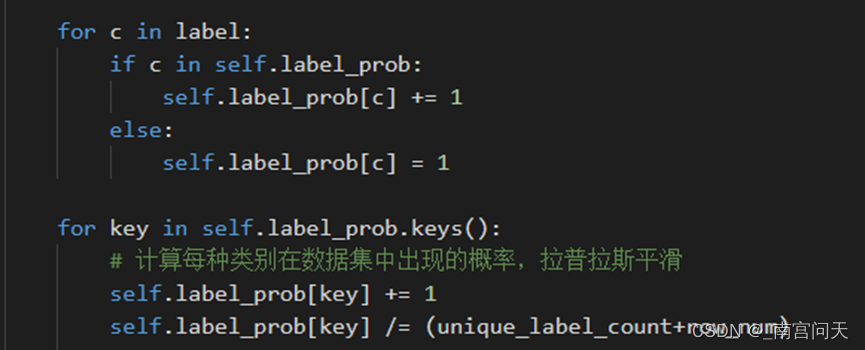
存储条件概率的字典初始化不需要修改,仍为:

计算条件概率时,调整分子和分母,实现拉普拉斯平滑:
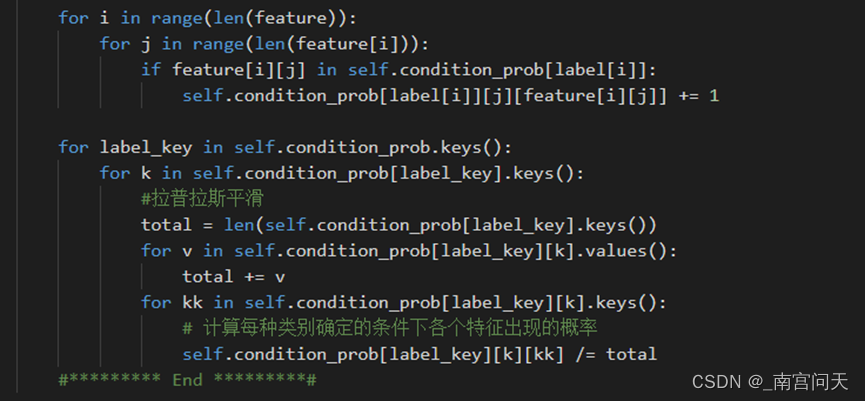
2、predict函数
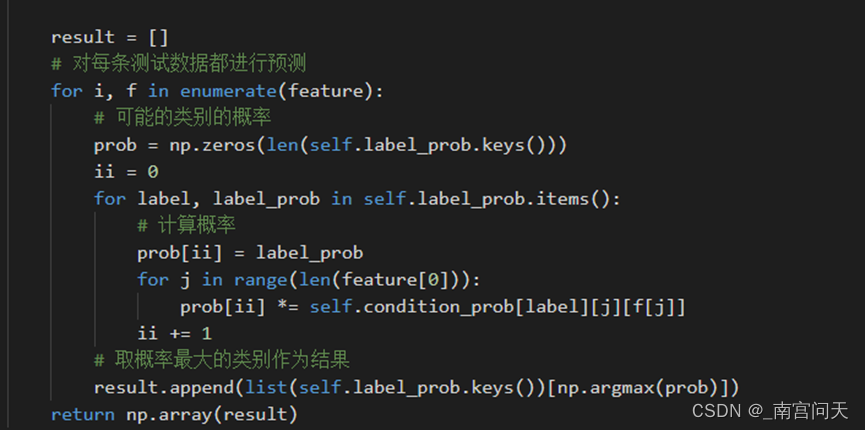
和第三关一样,预测的过程不变,仍按照贝叶斯公式计算,取在给定特征下,属于特定类别的概率最大的类别作为分类结果。
评测结果

第5关:新闻文本主题分类
、实验原理本关主要涉及到三个知识点。
1、文本的向量化——词频向量化
由于数据集中每一条数据都是很长的一个字符串,所以我们需要对数据进行向量化的处理。例如,I have a apple! I have a pen!可能需要将该字符串转换成向量如[10, 7, 0, 1, 2, 6, 22, 100, 8, 0, 1, 0]。
sklearn提供了实现词频向量化功能的CountVectorizer类。
即通过统计每个单词出现的频数,再把每个单词的频数进行向量化。
2、tf-idf构建文本向量
TF-IDF其实就是TF、IDF两部分组成。
TF(term frequency)表示词频。即一个文档中,词频越高的词权重越大。

IDF(Inverse Document Frequency)表示逆文档频率。即一个词出现的文档数越多,这个词的权重越低,一般会对IDF取对数。(如果不加log的话,IDF的结果相对会比较分散)

通过tf-idf计算出每个单词的权重,将单词权重进行向量化即可。
3、利用MultinomialNB对文本向量进行文本分类
MultinomialNB是sklearn中多项分布数据的朴素贝叶斯算法的实现,并且是用于文本分类的经典朴素贝叶斯算法。
在MultinomialNB实例化时alpha参数表示是否平滑处理。
alpha: 平滑因子。当等于1时,做的是拉普拉斯平滑;当小于1时做的是Lidstone平滑;当等于0时,不做任何平滑处理。MultinomialNB类中的fit函数实现了朴素贝叶斯分类算法训练模型的功能,predict函数实现了法模型预测的功能。
其中fit函数的参数如下:
X:大小为[样本数量,特征数量]的ndarry,存放训练样本Y:值为整型,大小为[样本数量]的ndarray,存放训练样本的分类标签而predict函数有一个向量输入:
X:大小为[样本数量,特征数量]的ndarry,存放预测样本2、实验内容
任务描述
本关任务:使用sklearn完成新闻文本主题分类任务。
重点:掌握如何使用sklearn提供的MultinomialNB类与文本向量化。
代码实现
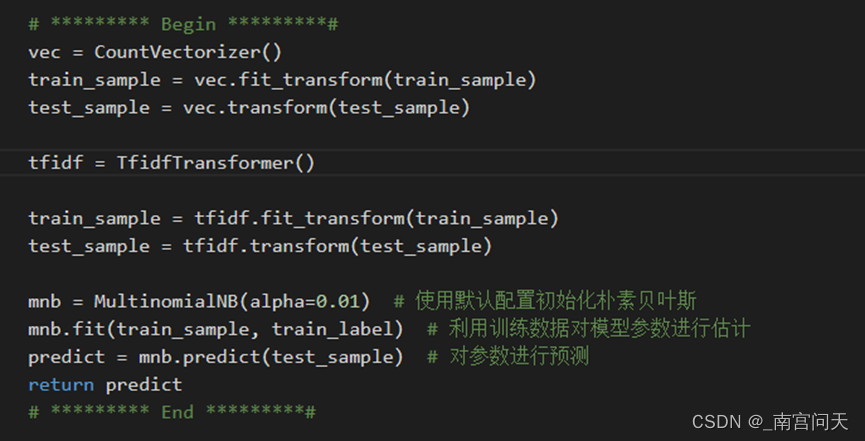
首先,采用CountVectorizer类对初始文本进行词频向量统计,再通过tfidf方法对词频向量转化为合理的文本向量,最后调用已经封装好的MultionomialNB类函数对数据集进行朴素贝叶斯训练和预测即可。这里alpha参数我采取的是0.01,即Lidstone平滑,采用默认的拉普拉斯平滑对数据的平滑处理不够,alpha要足够小,平滑效果强,预测成功率才高。
平滑的小知识
平滑的过程实际上是在每个特征的出现次数上加上一个小的常数 alpha,以确保即使某个特征在训练集中没有出现过,它的概率也不会变为零。
当 alpha 的值很小时,平滑效果较强,模型更倾向于学习训练数据中的细节,容易过拟合。而当 alpha 的值较大时,平滑效果较弱,模型更倾向于学习数据中的整体规律,有助于泛化到新的数据上。
评测结果

思考题
如何在参数学习或者其他方面提高算法的分类性能?
第三四关朴素贝叶斯算法实现比较简单,没有参数,但是条件独立性假设可能牺牲预测的准确性。
第五关的新闻文本分类中MultionomialNB的alpha参数的取值可能会对性能(预测准确率)产生影响,应该尽可能的让alpha参数小,这样平滑效果好,准确率高,但是可能产生更大的时空消耗。
实验总结
通过这次实验,我对贝叶斯公式有了更深刻的理解,学习了如何对数据集进行训练和分类预测,也学习了如何对数据集进行平滑处理,包括拉普拉斯平滑和Lidstone平滑等等,除此之外,我对文本数据向量化也有了进一步的了解,掌握了词频向量化和tf-idf向量化,同时,可以运用MultionomialNB类对数据集进行朴素贝叶斯训练和预测,总的来说,这是一次收获满满的实验。
附完整代码
第3关:朴素贝叶斯分类算法流程
import numpy as npclass NaiveBayesClassifier(object): def __init__(self): ''' self.label_prob表示每种类别在数据中出现的概率 例如,{0:0.333, 1:0.667}表示数据中类别0出现的概率为0.333,类别1的概率为0.667 ''' self.label_prob = {} ''' self.condition_prob表示每种类别确定的条件下各个特征出现的概率 例如训练数据集中的特征为 [[2, 1, 1], [1, 2, 2], [2, 2, 2], [2, 1, 2], [1, 2, 3]] 标签为[1, 0, 1, 0, 1] 那么当标签为0时第0列的值为1的概率为0.5,值为2的概率为0.5; 当标签为0时第1列的值为1的概率为0.5,值为2的概率为0.5; 当标签为0时第2列的值为1的概率为0,值为2的概率为1,值为3的概率为0; 当标签为1时第0列的值为1的概率为0.333,值为2的概率为0.666; 当标签为1时第1列的值为1的概率为0.333,值为2的概率为0.666; 当标签为1时第2列的值为1的概率为0.333,值为2的概率为0.333,值为3的概率为0.333; 因此self.label_prob的值如下: { 0:{ 0:{ 1:0.5 2:0.5 } 1:{ 1:0.5 2:0.5 } 2:{ 1:0 2:1 3:0 } } 1: { 0:{ 1:0.333 2:0.666 } 1:{ 1:0.333 2:0.666 } 2:{ 1:0.333 2:0.333 3:0.333 } } } ''' self.condition_prob = {} def fit(self, feature, label): ''' 对模型进行训练,需要将各种概率分别保存在self.label_prob和self.condition_prob中 :param feature: 训练数据集所有特征组成的ndarray :param label:训练数据集中所有标签组成的ndarray :return: 无返回 ''' #********* Begin *********# row_num = len(feature) col_num = len(feature[0]) for c in label: if c in self.label_prob: self.label_prob[c] += 1 else: self.label_prob[c] = 1 for key in self.label_prob.keys(): # 计算每种类别在数据集中出现的概率 self.label_prob[key] /= row_num # 构建self.condition_prob中的key self.condition_prob[key] = {} for i in range(col_num): self.condition_prob[key][i] = {} for k in np.unique(feature[:, i], axis=0): self.condition_prob[key][i][k] = 0 for i in range(len(feature)): for j in range(len(feature[i])): if feature[i][j] in self.condition_prob[label[i]]: self.condition_prob[label[i]][j][feature[i][j]] += 1 else: self.condition_prob[label[i]][j][feature[i][j]] = 1 for label_key in self.condition_prob.keys(): for k in self.condition_prob[label_key].keys(): total = 0 for v in self.condition_prob[label_key][k].values(): total += v for kk in self.condition_prob[label_key][k].keys(): #计算每种类别确定的条件下各个特征出现的概率 self.condition_prob[label_key][k][kk] /= total #********* End *********# def predict(self, feature): ''' 对数据进行预测,返回预测结果 :param feature:测试数据集所有特征组成的ndarray :return: ''' # ********* Begin *********# result = [] #对每条测试数据都进行预测 for i, f in enumerate(feature): #可能的类别的概率 prob = np.zeros(len(self.label_prob.keys())) ii = 0 for label, label_prob in self.label_prob.items(): #计算概率 prob[ii] = label_prob for j in range(len(feature[0])): prob[ii] *= self.condition_prob[label][j][f[j]] ii += 1 #取概率最大的类别作为结果 result.append(list(self.label_prob.keys())[np.argmax(prob)]) return np.array(result) #********* End *********#第4关:拉普拉斯平滑
import numpy as npclass NaiveBayesClassifier(object): def __init__(self): ''' self.label_prob表示每种类别在数据中出现的概率 例如,{0:0.333, 1:0.667}表示数据中类别0出现的概率为0.333,类别1的概率为0.667 ''' self.label_prob = {} ''' self.condition_prob表示每种类别确定的条件下各个特征出现的概率 例如训练数据集中的特征为 [[2, 1, 1], [1, 2, 2], [2, 2, 2], [2, 1, 2], [1, 2, 3]] 标签为[1, 0, 1, 0, 1] 那么当标签为0时第0列的值为1的概率为0.5,值为2的概率为0.5; 当标签为0时第1列的值为1的概率为0.5,值为2的概率为0.5; 当标签为0时第2列的值为1的概率为0,值为2的概率为1,值为3的概率为0; 当标签为1时第0列的值为1的概率为0.333,值为2的概率为0.666; 当标签为1时第1列的值为1的概率为0.333,值为2的概率为0.666; 当标签为1时第2列的值为1的概率为0.333,值为2的概率为0.333,值为3的概率为0.333; 因此self.label_prob的值如下: { 0:{ 0:{ 1:0.5 2:0.5 } 1:{ 1:0.5 2:0.5 } 2:{ 1:0 2:1 3:0 } } 1: { 0:{ 1:0.333 2:0.666 } 1:{ 1:0.333 2:0.666 } 2:{ 1:0.333 2:0.333 3:0.333 } } } ''' self.condition_prob = {} def fit(self, feature, label): ''' 对模型进行训练,需要将各种概率分别保存在self.label_prob和self.condition_prob中 :param feature: 训练数据集所有特征组成的ndarray :param label:训练数据集中所有标签组成的ndarray :return: 无返回 ''' #********* Begin *********# row_num = len(feature) col_num = len(feature[0]) unique_label_count = len(set(label)) for c in label: if c in self.label_prob: self.label_prob[c] += 1 else: self.label_prob[c] = 1 for key in self.label_prob.keys(): # 计算每种类别在数据集中出现的概率,拉普拉斯平滑 self.label_prob[key] += 1 self.label_prob[key] /= (unique_label_count+row_num) # 构建self.condition_prob中的key self.condition_prob[key] = {} for i in range(col_num): self.condition_prob[key][i] = {} for k in np.unique(feature[:, i], axis=0): self.condition_prob[key][i][k] = 1 for i in range(len(feature)): for j in range(len(feature[i])): if feature[i][j] in self.condition_prob[label[i]]: self.condition_prob[label[i]][j][feature[i][j]] += 1 for label_key in self.condition_prob.keys(): for k in self.condition_prob[label_key].keys(): #拉普拉斯平滑 total = len(self.condition_prob[label_key].keys()) for v in self.condition_prob[label_key][k].values(): total += v for kk in self.condition_prob[label_key][k].keys(): # 计算每种类别确定的条件下各个特征出现的概率 self.condition_prob[label_key][k][kk] /= total #********* End *********# def predict(self, feature): ''' 对数据进行预测,返回预测结果 :param feature:测试数据集所有特征组成的ndarray :return: ''' result = [] # 对每条测试数据都进行预测 for i, f in enumerate(feature): # 可能的类别的概率 prob = np.zeros(len(self.label_prob.keys())) ii = 0 for label, label_prob in self.label_prob.items(): # 计算概率 prob[ii] = label_prob for j in range(len(feature[0])): prob[ii] *= self.condition_prob[label][j][f[j]] ii += 1 # 取概率最大的类别作为结果 result.append(list(self.label_prob.keys())[np.argmax(prob)]) return np.array(result)第5关:新闻文本主题分类
from sklearn.feature_extraction.text import CountVectorizer # 从sklearn.feature_extraction.text里导入文本特征向量化模块from sklearn.naive_bayes import MultinomialNBfrom sklearn.feature_extraction.text import TfidfTransformerdef news_predict(train_sample, train_label, test_sample): ''' 训练模型并进行预测,返回预测结果 :param train_sample:原始训练集中的新闻文本,类型为ndarray :param train_label:训练集中新闻文本对应的主题标签,类型为ndarray :test_sample:原始测试集中的新闻文本,类型为ndarray ''' # ********* Begin *********# vec = CountVectorizer() train_sample = vec.fit_transform(train_sample) test_sample = vec.transform(test_sample) tfidf = TfidfTransformer() train_sample = tfidf.fit_transform(train_sample) test_sample = tfidf.transform(test_sample) mnb = MultinomialNB(alpha=0.01) # 使用默认配置初始化朴素贝叶斯 mnb.fit(train_sample, train_label) # 利用训练数据对模型参数进行估计 predict = mnb.predict(test_sample) # 对参数进行预测 return predict # ********* End *********#