指数平滑法简介
指数平滑法(Exponential Smoothing)是一种时间序列分析方法,用于处理时间序列数据的平滑和预测。
它的核心思想是基于过去的观测值来预测未来的值,同时对过去的数据赋予不同的权重,最近的观测值被赋予更大的权重,从而捕捉到时间序列的趋势和季节性模式。
指数平滑法的参数有3个——alpha、beta、gamma,分别对应数据、趋势、季节性。注意:参数值可以手动设定,参数值越大则模型越看重近期数据。若不设定参数,则软件会根据最大似然法计算得出参数值。
一次指数平滑法不考虑趋势与季节性,因此参数仅有alpha。
二次指数平滑法在一次的基础上进一步考虑了趋势,因此参数为alpha和beta。
三次指数平滑法在二次的基础上进一步考虑了季节性,因此参数为alpha、beta、gamma。此处需要注意的是季节性可以是加性(additive)或者乘性(multiplicative)的,这部分后续会详细解释。
一次指数平滑法(Simple Exponential Smoothing)
这是最简单的指数平滑方法,适用于没有趋势和季节性的时间序列。它使用单一平滑参数 alpha,将过去观测值的加权平均用于预测未来值。
模型公式
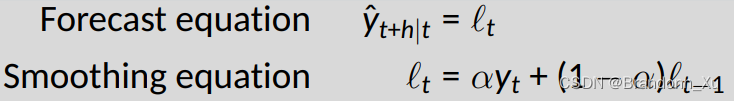
其中lt代表时间t时,数据的平滑值,yˆt+h为t+h时间的预测值。
即,一次指数平滑法的预测值始终等于t时刻的平滑值。
R代码实现
# 读取文件fc = read.table('AirPassengers.csv',sep=",",header=1)# 把数据转化为时间序列格式fc_ts = ts(fc$X,frequency=12,start=1949)# 导入forecast库library(forecast)# 拟合并预测未来20个样本点及其置信区间(默认为80% - 95%)pred = ses(fc_ts,h=20)# 绘制autoplot(pred)+autolayer(fitted(pred),series="Fitted")# 查看模型参数> pred$modelSimple exponential smoothing Call: ses(y = fc_ts, h = 20) Smoothing parameters: alpha = 0.9999 Initial states: l = 111.9892 sigma: 33.8299 AIC AICc BIC 1733.787 1733.958 1742.696 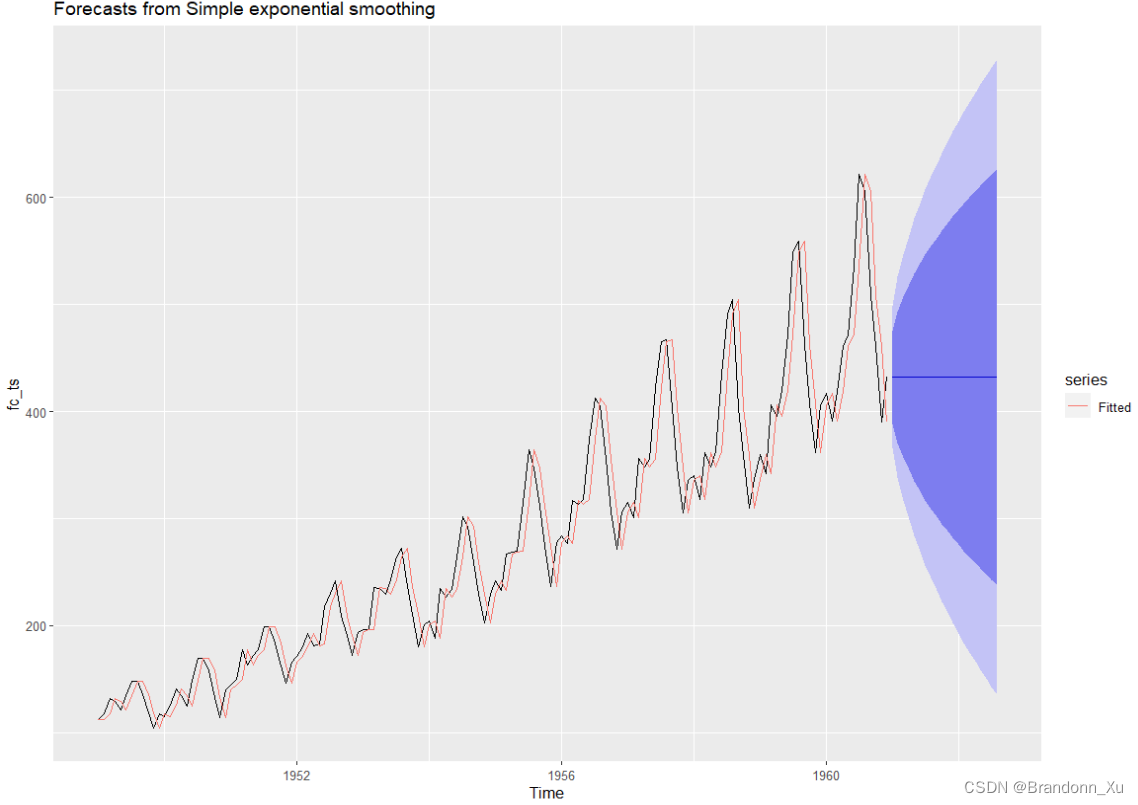
二次指数平滑法 —— 霍尔特线性指数平滑法(Holt's Exponential Smoothing)
适用于具有趋势但没有季节性的时间序列。它引入了两个平滑参数,alpha 和 beta,用于平滑观测值和趋势。
模型公式
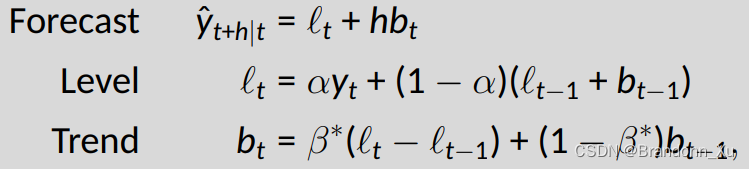
其中lt代表时间t时,数据的平滑值,yˆt+h为t+h时间的预测值。
相比一次指数平滑法,这里进一步考虑了过往数据的趋势,并引入beta参数进行拟合。
第一个公式中,lt及bt均为常数,h代表预测的步数(h=1,2,3...),因此得出结论:二次指数平滑法的预测值为一元一次线性函数。
R代码实现
# 拟合并预测pred = holt(fc$X,h=20)# 绘制autoplot(pred)+autolayer(fitted(pred),series="Fitted")# 查看模型参数与结果> pred$modelHolt's method Call: holt(y = fc$X, h = 20) Smoothing parameters: alpha = 0.9999 beta = 1e-04 Initial states: l = 119.7517 b = 1.5963 sigma: 34.0125 AIC AICc BIC 1737.295 1737.729 1752.144 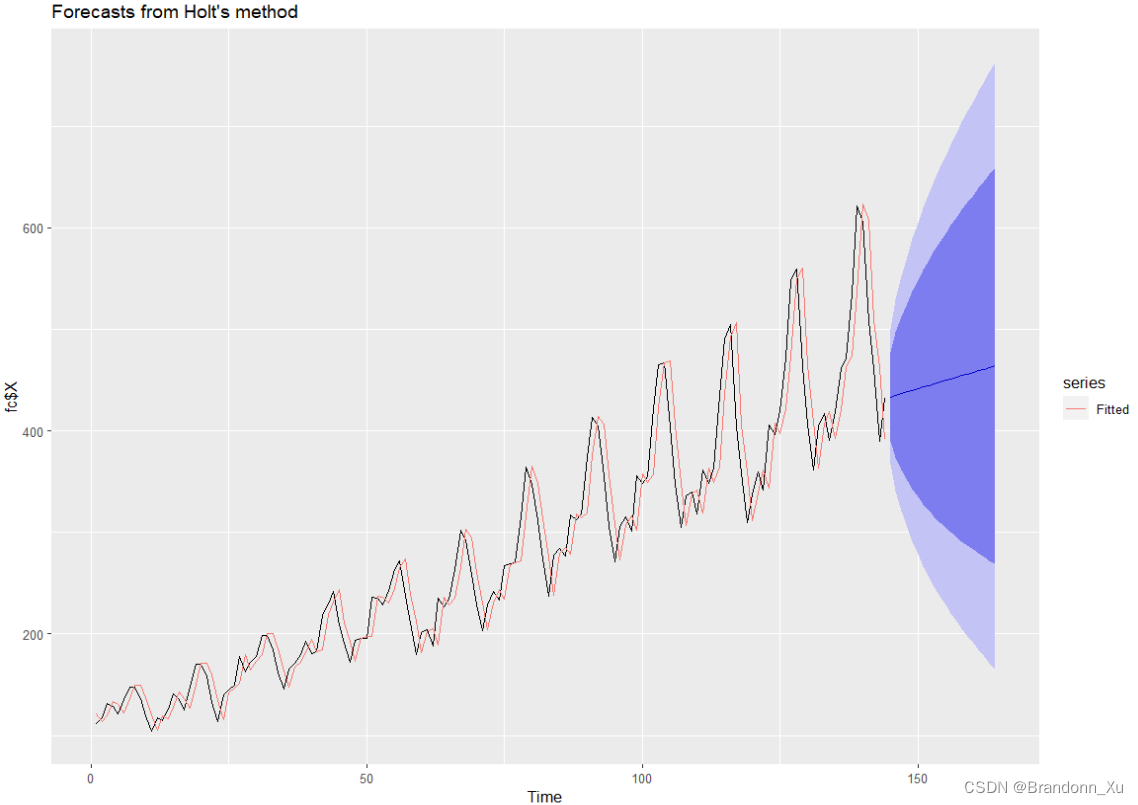
三次指数平滑法——霍尔特-温特斯季节性指数平滑法(Holt-Winters Exponential Smoothing)
适用于具有趋势和季节性的时间序列。它引入了三个平滑参数,alpha、beta 和 gamma,用于平滑观测值、趋势和季节性成分。
模型所考虑的季节性因素可以为加性(additive),也可以为乘性(multiplicative)。这两者之间的主要区别是季节性对整个时间序列的影响方式不同。
加性季节性:这是一种模型,其中季节性效应被视为与时间序列的整体趋势和大小无关的部分。换句话说,季节性波动是一种在时间序列上的额外的、相对固定的波动。例如,如果你在夏季卖出的冰淇淋数量通常是每月总销售量的固定增量,那么你可能会使用加性季节性。
举例:总销售 = 基本销售 + 季节性增量(夏季增加的销售)乘性季节性:这是一种模型,其中季节性效应被视为与时间序列的整体趋势和大小相关的部分。季节性波动与总体趋势成比例变化。例如,如果总销售量逐渐增加,那么季节性波动也会相应增加。
举例:总销售 = 基本销售 * 季节性比率(夏季销售与总销售的比率)选择加性还是乘性季节性通常取决于你的数据和季节性模式的性质。如果季节性波动与总体趋势无关,那么加性季节性可能更适合。如果季节性波动与总体趋势相关,那么乘性季节性可能更适合。
模型公式 - 加性
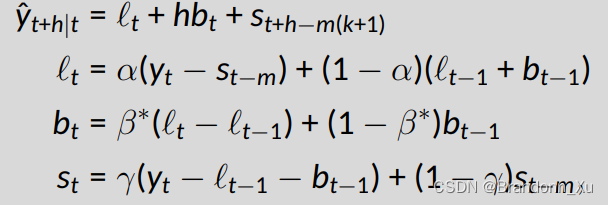
st即季节性因素。
R代码实现
# 拟合模型并预测pred = hw(ts(fc$X,frequency=12,start=1949),frequency=12,h=20,seasonal=c("additive"))# 绘制autoplot(pred)+autolayer(fitted(pred),series="Fitted")> pred$modelHolt-Winters' additive method Call: hw(y = ts(fc$X, frequency = 12, start = 1949), h = 20, frequency = 12) Smoothing parameters: alpha = 0.9935 beta = 2e-04 gamma = 6e-04 Initial states: l = 120.9608 b = 1.3934 s = -29.1816 -54.3842 -20.7169 15.0727 65.1554 66.1846 33.5822 -4.232 -8.0946 -3.8205 -34.3364 -25.2288 sigma: 18.0471 AIC AICc BIC 1565.872 1570.729 1616.359
模型公式 - 乘性
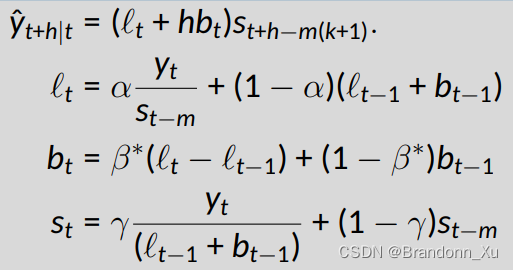
R代码实现
# 拟合并预测(设定参数seasonal=c("multiplicative"))pred = hw(ts(fc$X,frequency=12,start=1949),frequency=12,h=20,seasonal=c("multiplicative"))# 绘制autoplot(pred)+autolayer(fitted(pred),series="Fitted")# 查看模型结果> pred$modelHolt-Winters' multiplicative method Call: hw(y = ts(fc$X, frequency = 12, start = 1949), h = 20, seasonal = c("multiplicative"), Call: frequency = 12) Smoothing parameters: alpha = 0.3146 beta = 0.0071 gamma = 0.5977 Initial states: l = 120.3796 b = 1.7757 s = 0.9298 0.7946 0.9024 1.0451 1.1338 1.1388 1.0529 0.9638 1.0349 1.0807 0.9854 0.9378 sigma: 0.0407 AIC AICc BIC 1405.654 1410.511 1456.141 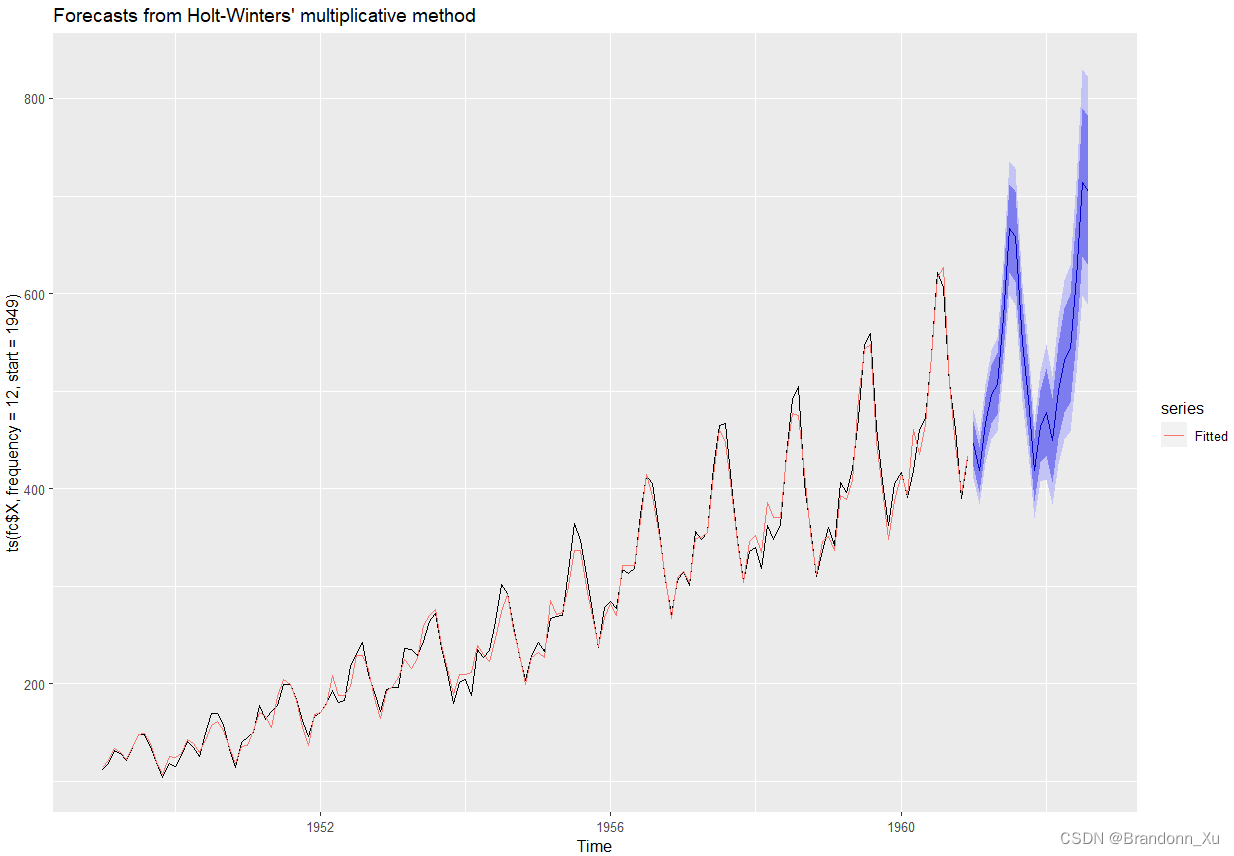
如何选择预测能力最准确的模型?
如何从上述4个模型中挑选出一个最适合当前数据的模型呢?
我们拟合模型的目的是预测时间序列数据,因此我们应该评估模型的预测能力。
一种可行的方法是:把一部分数据拿出来拟合模型,并得到一系列预测值,再把这些预测值与刚刚没有用于拟合模型的数据(真实值)做比较,测试其误差水平。这两个数据集也分别被称为训练集与验证集。
最后选择误差水平最低的一个模型即可。
选择训练集与验证集
# 选取训练集train = 1:120training = fc$X[train] # 选取训练集以外的作为交叉验证集test = fc$X[-train] 误差水平——RMSE最小均方根
library(Metrics)# 检验ses模型ses_pred_test = ses(training,h=length(test))rmse_1 = rmse(test,ses_pred_test$mean)# 检验holt模型holt_pred_test = holt(training,h=length(test))rmse_2 = rmse(test,holt_pred_test$mean)# 检验hw模型 加法hw_add_pred_test = hw(ts(training,frequency=12),h=length(test),seasonal=c("additive"))rmse_3 = rmse(test,hw_add_pred_test$mean)# 检验hw模型 乘法hw_mul_pred_test = hw(ts(training,frequency=12),h=length(test),seasonal=c("multiplicative"))rmse_4 = rmse(test,hw_mul_pred_test$mean)RMSE = c(rmse_1,rmse_2,rmse_3,rmse_4)print("模型与均方根误差:")data.frame(Methods,RMSE)[1] "模型与均方根误差:" Methods RMSE1 SES 137.331252 HOLT 117.112503 HW_ADD 91.223284 HW_MUL 37.18140显然,乘性三次指数平滑法具有最小误差水平,表明其预测能力在4个模型中最佳。