引言:
单调队列和单调栈都是一种数据结构,应用十分广泛,在蓝桥杯、ICPC、CCPC等著名编程赛事都是重点的算法,今天博主将自己对单调栈与单调队列的理解以及刷题的经验,用一篇博客分享给大家,希望对大家有所帮助,它们用于解决类似“寻找最大值与最小值”这样的问题。它们的区别在于如何维护数据的单调性。、
单调栈(Monotonic Stack):
单调栈是一种栈数据结构,只能在栈顶进行插入和删除操作。单调栈的特点是栈中的元素按照一定的单调性排列,常用的有单调递增和单调递减。在插入新元素时,如果新元素破坏了当前的单调性,则从栈顶删除一部分元素,直到满足单调性要求。这样可以保证栈中的元素保持单调性。单调栈的典型应用是在寻找下一个更大/更小元素的问题。单调队列(Monotonic Queue):
单调队列是一个双端队列,支持在队列两端进行插入和删除操作。单调队列的特点是队列中的元素按照一定的单调性排列,常用的有单调递增和单调递减。在插入新元素时,如果新元素破坏了当前的单调性,则在队尾删除一部分元素,直到满足单调性要求。这样可以保证队列中的元素保持单调性。单调队列的典型应用是在滑动窗口中寻找最大/最小值的问题。单调队列和单调栈都是用于维护数据的单调性,但单调队列是双端队列,用于在滑动窗口中寻找最大/最小值,而单调栈是栈数据结构,用于寻找下一个更大/更小元素。
下面我们对单调栈进行深度解析
单调栈:
单调栈是一种数据结构,通常用于解决一些与序列相关的问题,特别是在需要找到元素在序列中的「下一个更大元素」或「下一个更小元素」的情况下。单调栈可以用于在线性时间复杂度内解决这些问题。

单调栈分为单调递增栈和单调递减栈两种类型:
1.单调递增栈:
栈中元素从栈底到栈顶递增。在处理序列时,当遇到一个元素时,如果该元素比栈顶元素大,就可以将栈顶元素出栈,直到栈为空或者栈顶元素大于等于当前元素。这样,栈中的元素就是在当前元素之前且比当前元素小的元素。
2.单调递减栈:
栈中元素从栈底到栈顶递减。在处理序列时,当遇到一个元素时,如果该元素比栈顶元素小,就可以将栈顶元素出栈,直到栈为空或者栈顶元素小于等于当前元素。这样,栈中的元素就是在当前元素之前且比当前元素大的元素。
使用单调栈的一般步骤如下:
1.创建一个空栈。
2.遍历待处理的序列,对于每个元素执行以下操作:
1.如果当前元素比栈顶元素大(或小,取决于是递增栈还是递减栈),则持续将栈顶元素出栈,直到栈为空或者栈顶元素满足某种条件(例如比当前元素大或小)。
2.记录弹出的元素,说明他是单调递减栈或单调递增栈第一个不满足的元素,可以在此元素根据题意进行操作
3.如果栈不为空,比较当前元素与栈顶元素的大小:
4..将当前元素入栈。
单调栈常用于解决一些数组或序列相关的问题,如找到下一个更大元素、下一个更小元素。
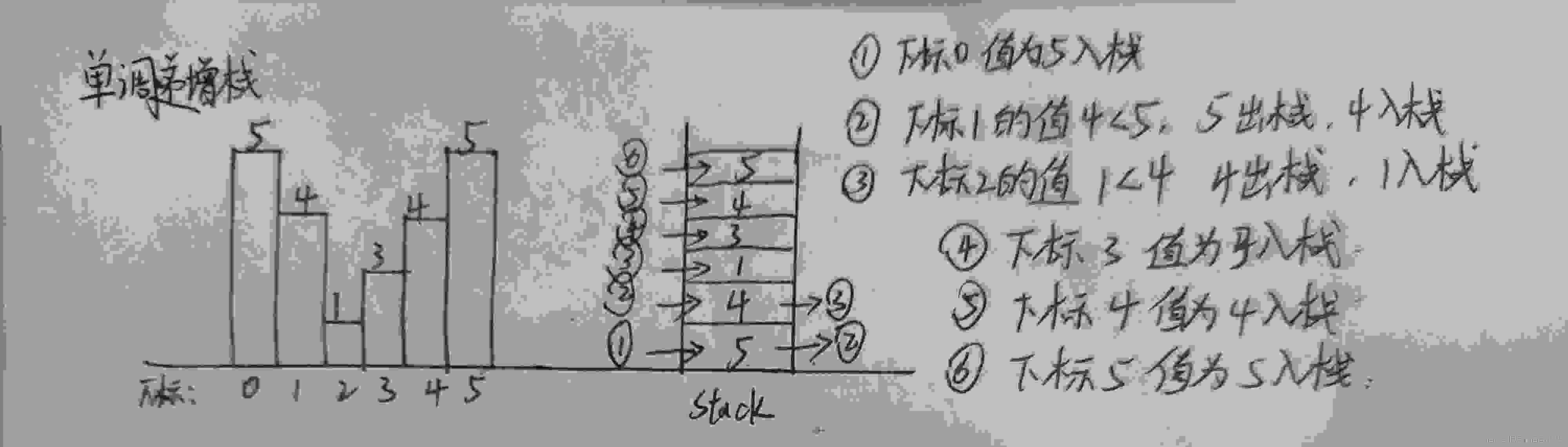
模板奉上:
第一种使用stack
stack<int> st; // 单调栈,存储元素的下标nums[n]=-1; //多加一个-1元素,防止到最后栈中还是单调递增栈,未能更新最大值//单调递减栈就是nums[n]=0x3f3f3f; for (int i = 0; i < n; i++) { while (!st.empty() && nums[i] <= nums[st.top()]) {//不满足单调递增栈,就开始更新 res[st.top()] = i; // 弹出元素直到满足单调递增 st.pop(); } st.push(i);//下标入队} 第二种手写一个单调栈
int work3(int h[]) { // stk 从下标 1 开始存储 int top = 0, res = 0; // 遍历到 m + 1 的位置 // 因为是在出栈时统计,为保证遍历结束时所有下标都会被统计,默认 m + 1 位置存储 0 for (int i = 1; i <= m + 1; ++ i ) { while (top && h[stk[top]] >= h[i]) { int l = stk[top -- ]; //此处添加代码根据题意进行操作 } stk[ ++ top] = i; } return res;}实战演练——单调栈练习题
【模板】单调栈 - 洛谷
#include<iostream>#include<stack>using namespace std;int n;const int N=3e6+5;int a[N],res[N];stack<int> stk;int main(){ cin>>n; for(int i=1;i<=n;i++){ cin>>a[i]; } for(int i=n;i>=1;i--){ while(!stk.empty()&&a[stk.top()]<=a[i]){ stk.pop(); } res[i]=stk.empty()?0:stk.top(); stk.push(i); } for(int i=1;i<=n;i++){ cout<<res[i]<<" "; } return 0;}131. 直方图中最大的矩形 - AcWing题库
#include<iostream>#include<stack>using namespace std;typedef long long ll;const int N=1e5+5;int n;ll a[N];ll res;int main(){while(cin>>n&&n){for(int i=0;i<n;i++){cin>>a[i];}a[n]=-1;//单调递增栈,不要忘记最后一个赋值为-1,不然跟上图里面的数据不会更新res=0;stack<int> st;//使用STL的stackfor(int i=0;i<=n;i++){while(!st.empty()&&a[st.top()]>=a[i]){//每当不符合说明要开始更新最大面积了int index=st.top();//每次弹出来跟当前不满足的值进行计算最大面积st.pop();int l=st.empty()?-1:st.top();res=max(res,(i-l-1)*a[index]);//i-l-1为宽,a[index]为高}st.push(i);//下标入栈}cout<<res<<endl;}return 0;}1574. 接雨水 - AcWing题库
#include<iostream>#include<stack>using namespace std;const int N=1e5+5;int n;int a[N];int ans;stack<int> st;int main(){cin>>n;for(int i=0;i<n;i++){cin>>a[i];} //由于寻找第一个右边比他大的元素,为单调递减栈,不需要再加一个-1,此题边界不可以接雨水,所以不用赋值最后一位for(int i=0;i<n;i++){while(!st.empty()&&a[st.top()]<a[i]){//当前值大于栈顶元素,开始更新雨水面积int dex=st.top();st.pop();int left=st.empty()?i-1:st.top();//i-1与上题不同具体问题具体分析,此题若栈中没有元素,自己自成一个,不可能接住水与下面(i-left-1),left带入为计算0int h=min(a[left],a[i])-a[dex];//高度ans+=h*(i-left-1);}st.push(i);}cout<<ans<<endl;return 0;}1413. 矩形牛棚 - AcWing题库
这一题之前蓝桥杯每日一题写过题解,可以看过来:AcWing 1413. 矩形牛棚(每日一题)-CSDN博客
总结:
单调栈在题目中应用很广泛,是一名算法选手所必须掌握的基础算法,在题目中遇到寻找最大最小的元素,或者对元素进行找最大最小的问题可以考虑单调栈,单调栈主要适用于一些需要找到“下一个更大(或更小)元素”的问题。通过维护一个单调递增(或递减)的栈,可以高效地找到下一个更大(或更小)元素。在实际应用中,需要注意栈的边界条件及特殊情况的处理。单调栈的时间复杂度通常为O(n),其中n为元素的个数。利用单调栈可以在题目规定的时间可以解决问题。博主在学习单调栈的过程中将自己由开始学习到逐渐理解,期间的一些疑问以及自己所收获的凝结成此篇文章,望对大家有所帮助,文章尚有不足之处,恳请各位大佬指出,感激不尽。
下一篇更新:优先队列
