一、什么是机器学习
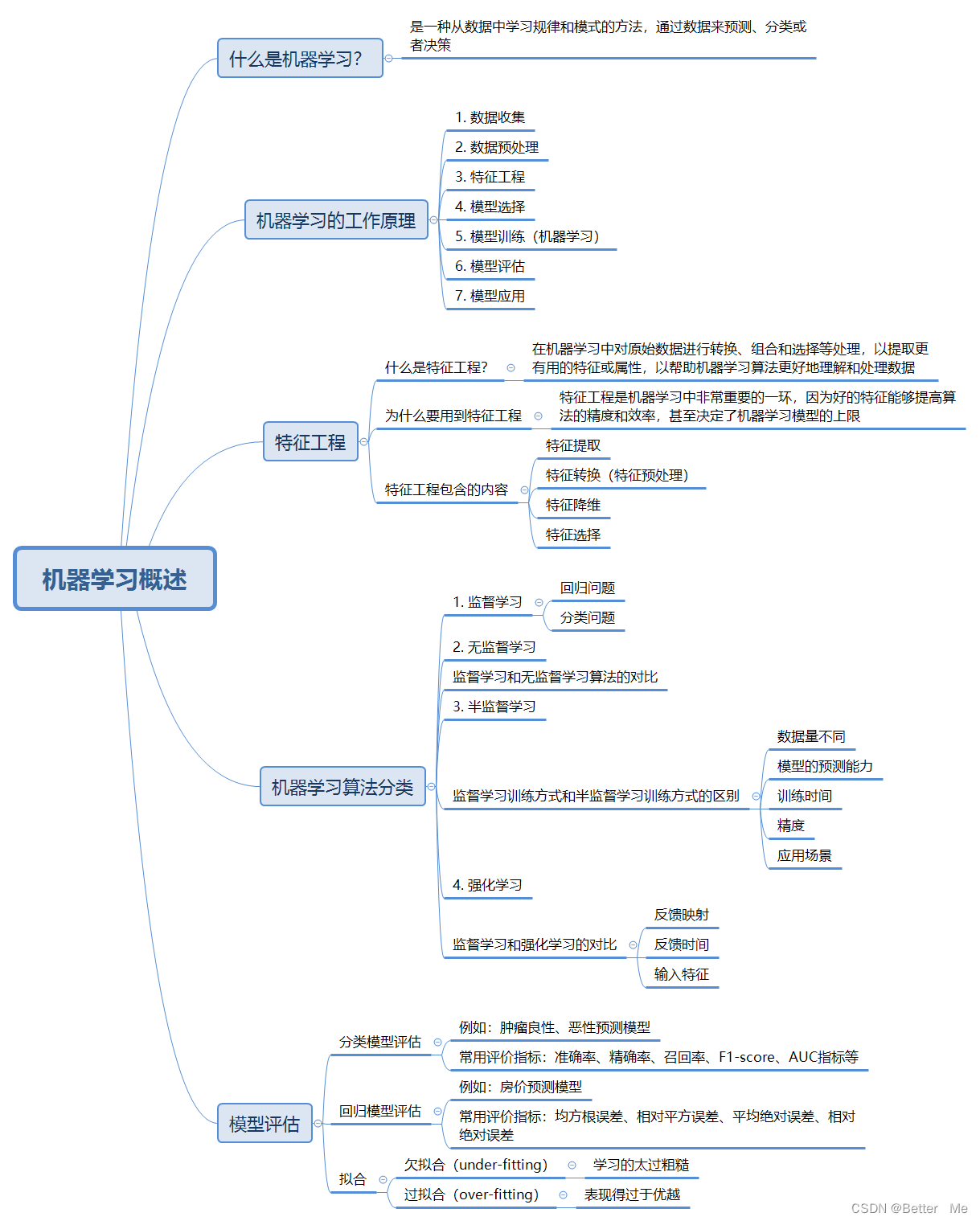
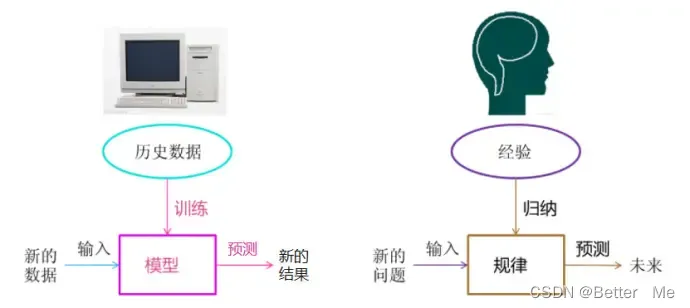
机器学习是一种人工智能技术,通过对数据的学习和分析,让计算机系统自动提高其性能。简而言之,机器学习是一种从数据中学习规律和模式的方法,通过数据来预测、分类或者决策。
二、机器学习的工作原理
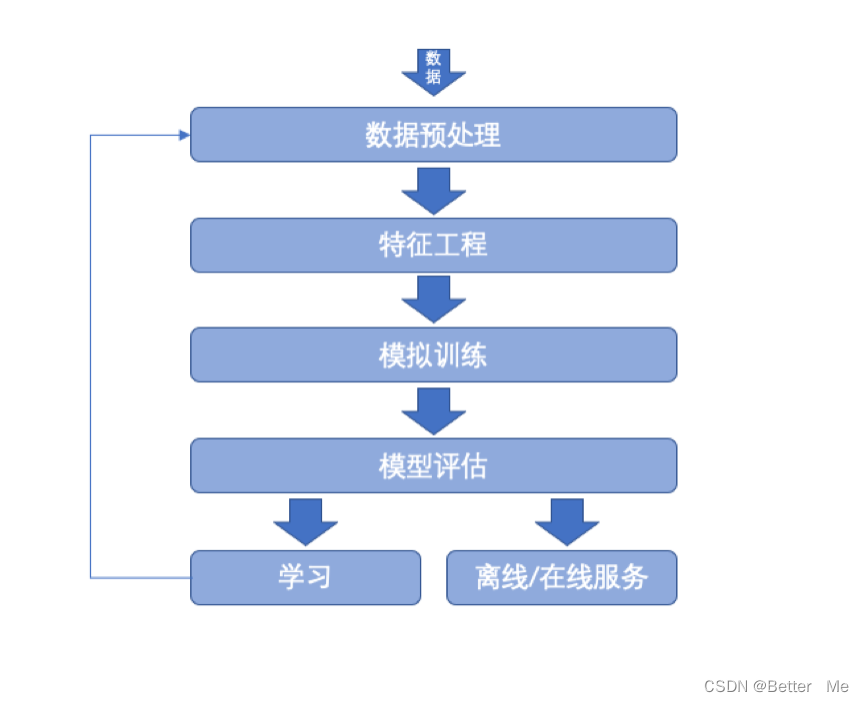
机器学习的工作原理主要包括以下几个步骤:
数据收集:首先需要收集数据并将其转化为可以计算的形式,例如数值、文本或图像等。
数据预处理:数据收集后,需要对数据进行清洗、去除异常值、缺失值处理、特征选择等预处理步骤。
特征工程: 是指在机器学习中对原始数据进行转换、组合和选择等处理,以提取更有用的特征或属性,以帮助机器学习算法更好地理解和处理数据。简而言之,特征工程就是对原始数据进行预处理,以提取有用信息来辅助机器学习。
模型选择:根据问题的特点和数据的特征选择适合的机器学习算法和模型。
模型训练(机器学习):利用已有数据对所选的机器学习模型进行训练,从而使模型能够学习数据中的规律和模式。
模型评估:训练完成后,需要对模型进行评估和调整,以检查其性能和精度,并进行优化。
模型应用:经过训练和优化后,机器学习模型可以用于新数据的预测、分类、聚类等任务。
三、数据简介
数据简介
在数据集中一般:
一行数据我们称为一个样本一列数据我们称为一个特征有些数据有目标值(标签值),有些数据没有标签值数据类型构成
数据类型一:特征值+目标值(目标值是连续的和离散的)数据类型二:只有特征值,没有目标值数据分割
机器学习一般的数据集会划分为两个部分: 训练数据:用于训练,构建模型测试数据:在模型检验时使用,用于评估模型是否有效 划分比例: 训练集:70% 80% 75%测试集:30% 20% 25%四、特征工程
什么是特征工程
是指在机器学习中对原始数据进行转换、组合和选择等处理,以提取更有用的特征或属性,以帮助机器学习算法更好地理解和处理数据。简而言之,特征工程就是对原始数据进行预处理,以提取有用信息来辅助机器学习。
为什么要用到特征工程
特征工程是机器学习中非常重要的一环,因为好的特征能够提高算法的精度和效率,甚至决定了机器学习模型的上限。因此,进行特征工程需要根据具体问题和数据特点进行灵活选择和处理,以达到最佳效果。
特征工程包含的内容
特征提取:从原始数据中提取特征,通常是利用数学和统计方法对数据进行转换和降维,例如主成分分析(PCA)、奇异值分解(SVD)等。特征转换(特征预处理):将提取的特征进行转换,以符合算法的需求,例如将类别特征转换为数值特征,或者对数值特征进行标准化。特征降维:指在某些限定条件下,降低随机变量(特征)个数,得到一组“不相关”主变量的过程特征选择:根据特征的重要性和相关性等指标,选择最具有代表性的特征,以减少计算复杂度和提高算法性能。五、机器学习算法分类
监督学习
输入数据是由输入特征值和目标值所组成。函数的输出可以是一个连续的值(称为回归),或是输出有限个离散值(称为分类)
回归问题
例如:预测房价,根据集拟合出一条连续曲线
分类问题
例如:根据肿瘤特征判断良性还是恶性,得到的是结果是“良性”或者“恶性”,是离散的
无监督学习
输入数据是由输入特征值组成,没有目标值。输入数据没有被标记,也没有确定的结果,样本数据类别未知;需要根据样本间的相似性对样本集进行类别划分。
有监督,无监督算法对比: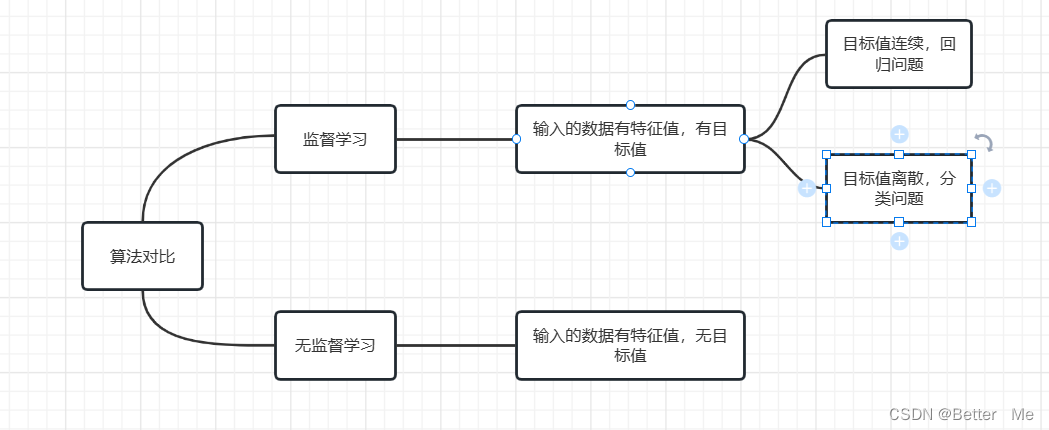
半监督学习
训练集同时包含有标记样本数据和未标记样本数据
监督学习训练方式和半监督学习训练方式的区别: 数据量不同:监督学习需要大量有标签的数据来进行训练,而半监督学习则可以利用部分有标签数据和大量无标签数据进行训练。模型的预测能力:监督学习的模型在处理未知数据时需要有标签的数据作为参考,而半监督学习的模型可以更好地利用未标记数据来提高预测能力。训练时间:由于半监督学习使用了更多的数据进行训练,因此需要更长的时间来完成模型的训练。精度:半监督学习的模型在某些情况下可以比监督学习的模型具有更好的精度,尤其是当标记数据很少的时候。应用场景:监督学习适用于已经有标签数据的问题,例如分类和回归等问题,而半监督学习适用于数据集标签数量较少或标签数据难以获得的问题。强化学习
实质就是make decisions问题,即自动进行决策,并且可以做连续决策。强化学习的的目标就是获得最多的累计奖励。
强化学习的五个元素:
agent、action、reward、environment、observation
监督学习的强化学习的对比:
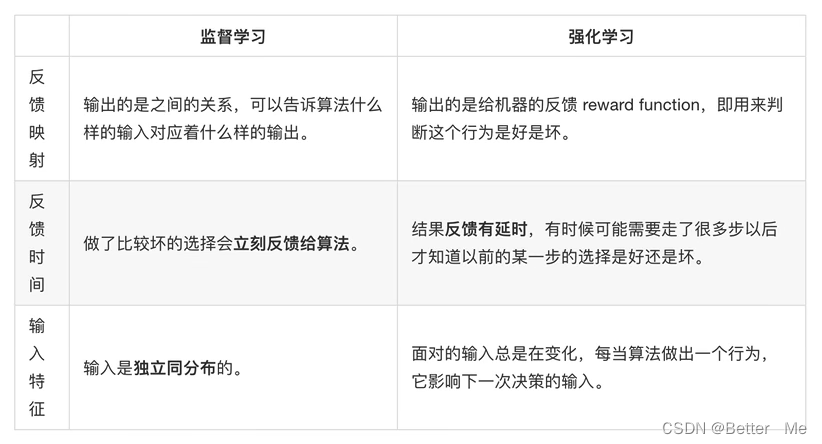
四种学习算法的小结
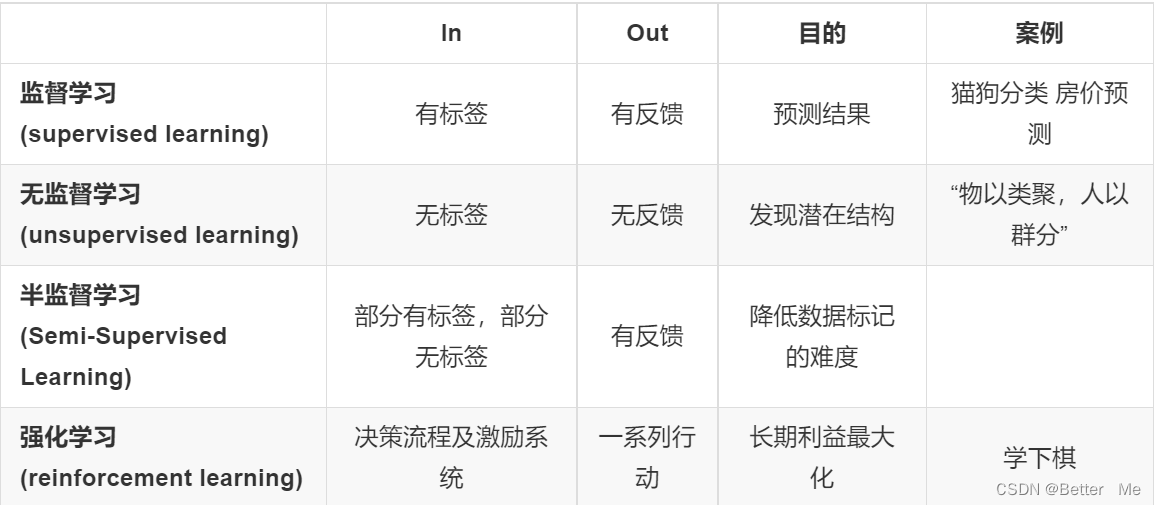
六、模型评估
模型评估是模型开发过程不可或缺的一部分。它有助于发现表达数据的最佳模型和所选模型将来工作的性能如何。
按照数据集的目标值不同,可以把模型评估分为分类模型评估和回归模型评估。
分类模型评估
例如:肿瘤良性、恶性预测模型
准确率:
预测正确的数占样本总数的比例。
其他评价指标:
精确率、召回率、F1-score、AUC指标等。
回归模型评估
例如:房价预测模型
均方根误差(Root Mean Squared Error,RMSE)
RMSE是一个衡量回归模型误差率的常用公式。不过,它仅能比较误差是相同单位的模型。
均方根误差公式

举例:
假设有一个房价预测模型,只有五个样本,对应的
真实值为:100,120,125,230,400
预测值为:105,119,120,230,410
则均方根误差求解得:
R M S E = [ ( 105 − 100 ) 2 + ( 119 − 120 ) 2 + ( 120 − 125 ) 2 + ( 230 − 230 ) 2 + ( 410 − 400 ) 2 ] 5 2 = 5.495 RMSE=\sqrt[2]{\frac{[(105-100)^2+(119-120)^2+(120-125)^2+(230-230)^2+(410-400)^2]}{5}}=5.495 RMSE=25[(105−100)2+(119−120)2+(120−125)2+(230−230)2+(410−400)2] =5.495
拟合
模型评估用于评价训练好的模型的表现效果,其表现效果大致可以分为两类:过拟合、欠拟合。
欠拟合(under-fitting):模型学习的太过粗糙,在训练集中的样本数据特征关系都没有学出来。过拟合(over-fitting):所建的机器学习模型或者是深度学习模型在训练样本中表现得过于优越,导致在测试数据集中表现不佳。