目录
一 、实验目的
二 、实验内容
三 、实验原理
四 、实验过程
数据处理
1.1数据读入
1.2缺失值处理
1.3数据归一化
1.4数据集乱序
1.6数据集分批次
模型设计与配置
2.1 构建前向网络结构,定义假设空间
2.2初始化参数w和b,使用标准正态分布随机生成
训练网络
3.1外层循环 epoch
3.2内层循环
3.2.1前向计算
3.2.2 损失函数值
3.2.3反向传播更新参数值
3.5打印一个epoch的训练集测试集损失函数值
封装各函数
4.1归一化两个函数
4.1.1最大最小归一化
4.1.2均值归一化
4.2封装数据集加载
4.3封装网络架构
4.4封装训练函数
4.5训练只需要简单几步
尝试不同归一化方式
遍历学习率寻找最优
改变数据划分比例
五、实验总结与心得体会
一 、实验目的
熟悉 python 的语法使用掌握深度学习的全过程深刻理解并且掌握全连接神经网络的工作原理二 、实验内容
用最简单的线性回归模型解决这个问题,并用 python 的 numpy 库搭建一个单层的全连接神经网络,用于拟合这个线性回归函数,来预测 Boston 的房价。
三 、实验原理
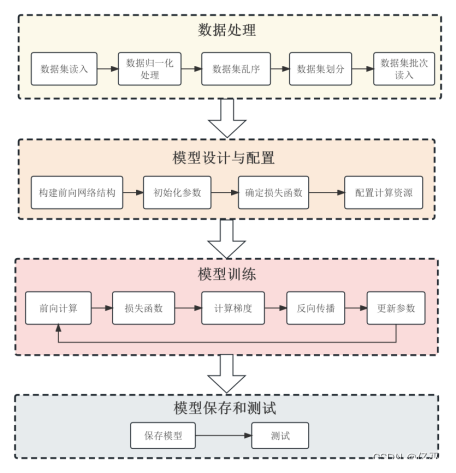
构建模型和完成训练的程序图
本实验使用单层全连接网络结构,如下图所示
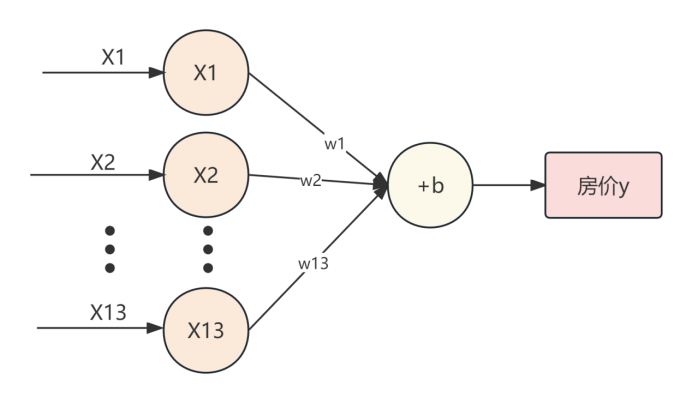
房价模型单层全连接网络结构图
四 、实验过程
数据处理
1.1数据读入
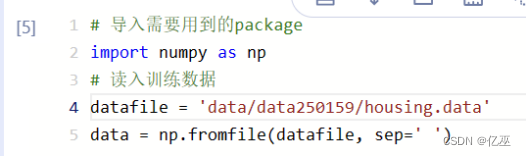
使用numpy的fromfile()函数读入训练数据
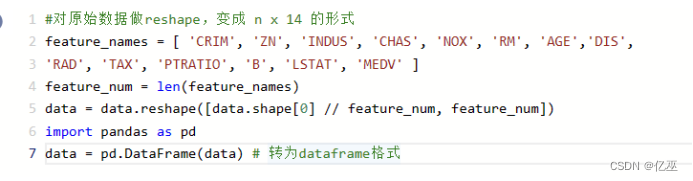
由于数据刚读入都是没有确定行和列的,所以需要对原始数据做reshape,变成 n x 14 的形式
查看数
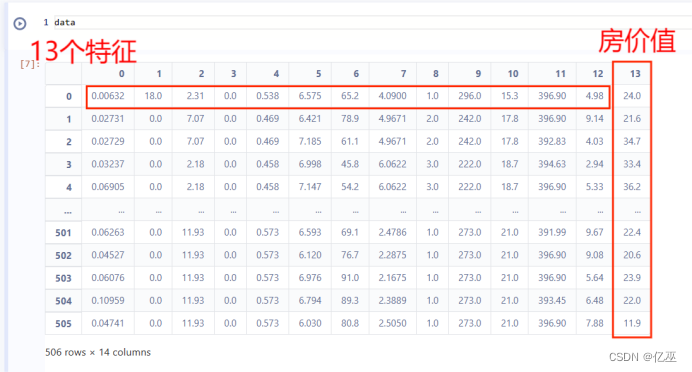
1.2缺失值处理
缺失值个数为0,无缺失值,不做其他处理
1.3数据归一化
使用最大最小归一化,归一化函数如下图所示
# 定义最大最小归一化函数def min_max_scaling(column): min_val = column.min() max_val = column.max() scaled_column = (column - min_val) / (max_val - min_val) return scaled_column# 对DataFrame的进行最大最小归一化normalized_df = data.apply(min_max_scaling, axis=0)
查看归一化后的数据
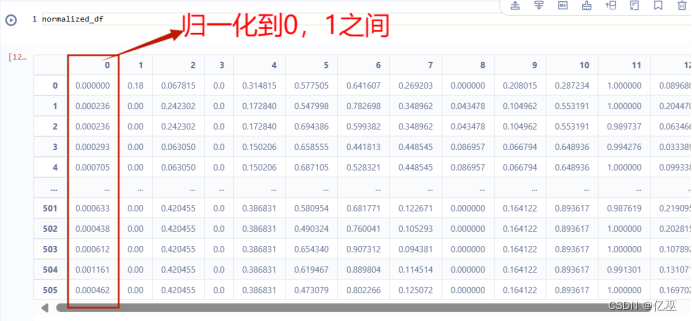
1.4数据集乱序
对DataFrame的索引进行随机重排,然后使用新的索引重新排序数据列
# 对DataFrame的索引进行随机重排shuffled_index = np.random.permutation(normalized_df.index)# 使用新的索引重新排序DataFrame的行shuffled_df = normalized_df.loc[shuffled_index]
1.5划分数据集
数据集划分比例为训练集:测试集=8:2
# 数据集划分ratio = 0.8offset = int(shuffled_df.shape[0] * ratio)training_data = shuffled_df[:offset]test_data=shuffled_df[offset:]training_data
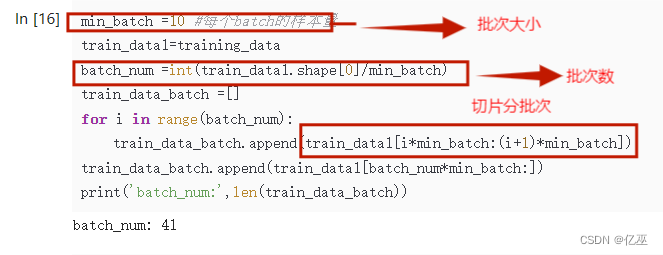
1.6数据集分批次
设定每个批次大小为10
batch_num为数据大小除以批次大小后取整,得到一个批次数,由次批次数来对数据集切片分批次
min_batch =10 #每个batch的样本量train_data1=training_databatch_num =int(train_data1.shape[0]/min_batch)train_data_batch =[]for i in range(batch_num): train_data_batch.append(train_data1[i*min_batch:(i+1)*min_batch])train_data_batch.append(train_data1[batch_num*min_batch:]) print('batch_num:',len(train_data_batch))
训练集批次数为41
测试集采用同样的方式,批次数为11

min_batch =10 #每个batch的样本量test_data1=test_databatch_num =int(test_data1.shape[0]/min_batch)test_data_batch =[]for i in range(batch_num): test_data_batch.append(test_data1[i*min_batch:(i+1)*min_batch])test_data_batch.append(test_data1[batch_num*min_batch:]) print('batch_num:',len(test_data_batch))模型设计 与配置
2.1 构建前向网络结构,定义假设空间
假设空间y=xw+b

2.2初始化参数w和b,使用标准正态分布随机生成

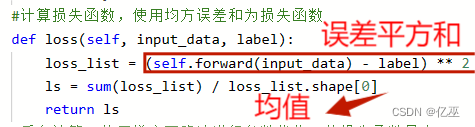
2.3计算损失函数
采用均方误差和为损失函数
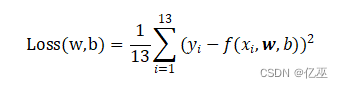
2.4后向计算,采用梯度下降法更新模型参数
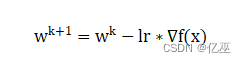

训练网络
3.1外层循环 epoch
![]()
![]()
3.2内层循环
设置学习率lr=0.001
3.2.1前向计算
初始化网络,特征数为13
![]()
3.2.2 损失函数值

3.2.3反向传播更新参数值
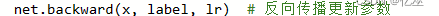
3.3计算测试集损失函数值

3.4计算一个epoch的损失函数值

3.5打印一个epoch的训练集测试集损失函数值
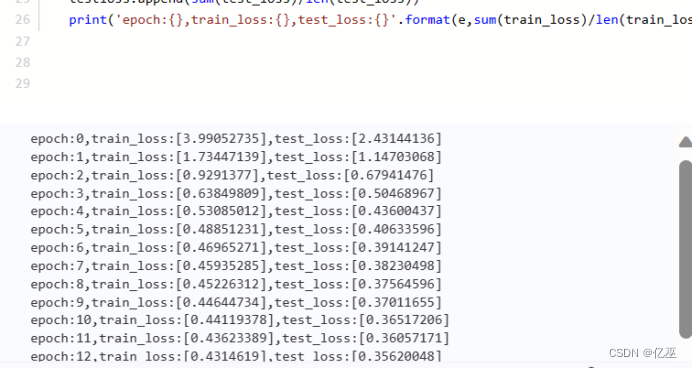
3.6可视化随epoch变化的损失函数值loss
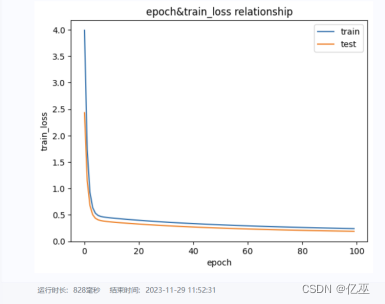
封装各函数
4.1归一化两个函数
4.1.1最大最小归一化
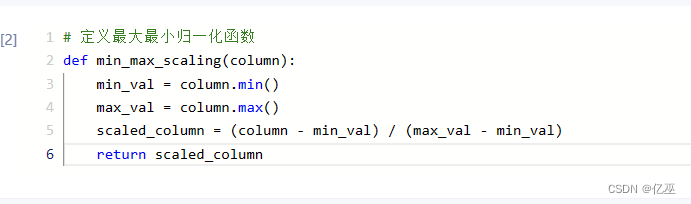
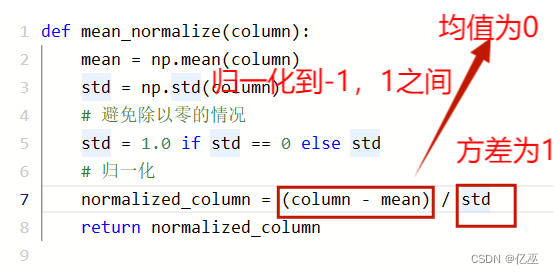
4.1.2均值归一化
即z-score归一化,将特征归一化到均值为0,方差为1
4.2封装数据集加载
def load_data(data_path,nomalize,ratio): data = np.fromfile(data_path, sep=' ') #对原始数据做reshape,变成 n x 14 的形式 feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ] feature_num = len(feature_names) data = data.reshape([data.shape[0] // feature_num, feature_num]) data = pd.DataFrame(data) # 转为dataframe格式 #归一化 normalized_df = data.apply(nomalize, axis=0) #数据集乱序 # 对DataFrame的索引进行随机重排 shuffled_index = np.random.permutation(normalized_df.index) # 使用新的索引重新排序DataFrame的行 shuffled_df = normalized_df.loc[shuffled_index] # 数据集划分 offset = int(shuffled_df.shape[0] * ratio) training_data = shuffled_df[:offset] test_data=shuffled_df[offset:] #数据集分批次 min_batch =10 #每个batch的样本量 train_data1=training_data batch_num =int(train_data1.shape[0]/min_batch) train_data_batch =[] for i in range(batch_num): train_data_batch.append(train_data1[i*min_batch:(i+1)*min_batch]) train_data_batch.append(train_data1[batch_num*min_batch:]) print('batch_num:',len(train_data_batch)) test_data1=test_data batch_num =int(test_data1.shape[0]/min_batch) test_data_batch =[] for i in range(batch_num): test_data_batch.append(test_data1[i*min_batch:(i+1)*min_batch]) test_data_batch.append(test_data1[batch_num*min_batch:]) print('batch_num:',len(test_data_batch)) return train_data_batch,test_data_batch
4.3封装网络架构
class Network(object): def __init__(self, input_num): # 初始化参数w和b,使用标准正态分布随机生成 self.w = np.random.normal(0, 1, (input_num, 1)) # 将 self.w 设为列向量 self.b = np.random.normal(0, 1) #前向计算y值 def forward(self, input_data): y = input_data @ self.w + self.b # 不再进行转置操作 return y #计算损失函数,使用均方误差和为损失函数 def loss(self, input_data, label): loss_list = (self.forward(input_data) - label) ** 2 ls = sum(loss_list) / loss_list.shape[0] return ls #后向计算,使用梯度下降法进行参数优化,使损失函数最小 def backward(self, input_data, label, lr): y = self.forward(input_data) error = y - label.reshape(1, -1) # 不再使用to_numpy() reshape gradient_w = (error.T @ input_data) / input_data.shape[0] gradient_w = gradient_w[0] gradient_b = np.sum(error) / input_data.shape[0] self.w -= lr * gradient_w.reshape(-1, 1) # 注意这里的 reshape 操作 self.b -= lr
4.4封装训练函数
def train(epoch,lr,data_path,normalize,ratio): trainloss = [] testloss = [] net=Network(13) train_data_batch,test_data_batch=load_data(data_path,normalize,ratio) # 超参数设置 for e in range(epoch): # 训练 train_loss=[] test_loss=[] for data in train_data_batch: x = data.iloc[:, :13].to_numpy() # 前13个值是特征值 label = data.iloc[:, -1].to_numpy().reshape(-1, 1) # 转换为NumPy数组再reshape loss = net.loss(x, label) # 得到训练的loss值 train_loss.append(loss) net.backward(x, label, lr) # 反向传播更新参数 #测试 for data in test_data_batch: x = data.iloc[:, :13].to_numpy() # 将DataFrame转换为NumPy数组 label = data.iloc[:, -1].to_numpy().reshape(-1, 1) # 转换为NumPy数组再reshape loss=net.loss(x, label) test_loss.append(loss) # 得到测试的Loss值 trainloss.append(sum(train_loss)/len(train_loss)) testloss.append(sum(test_loss)/len(test_loss)) #print('epoch:{},train_loss:{},test_loss:{}'.format(e,sum(train_loss)/len(train_loss),sum(test_loss)/len(test_loss))) print('best_train_loss:{},best_test_loss:{}'.format(min(trainloss),min(testloss))) import matplotlib.pyplot as plt # 绘制折线图 plt.plot(trainloss, label='train') plt.plot(testloss, label='test') # 添加标题和标签 plt.title('epoch&train_loss relationship') plt.xlabel('epoch') plt.ylabel('train_loss') # 显示图例 plt.legend() # 显示图表 plt.show()
4.5训练只需要简单几步
epoch = 100lr = 0.001 # 学习率data_path='data/data250159/housing.data'ratio=0.8train(epoch,lr,data_path,min_max_scaling,ratio)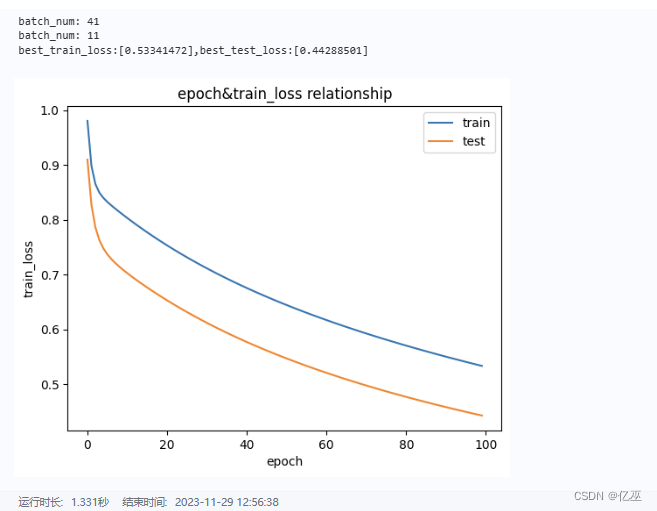
尝试不同归一化方式
使用均值归一化

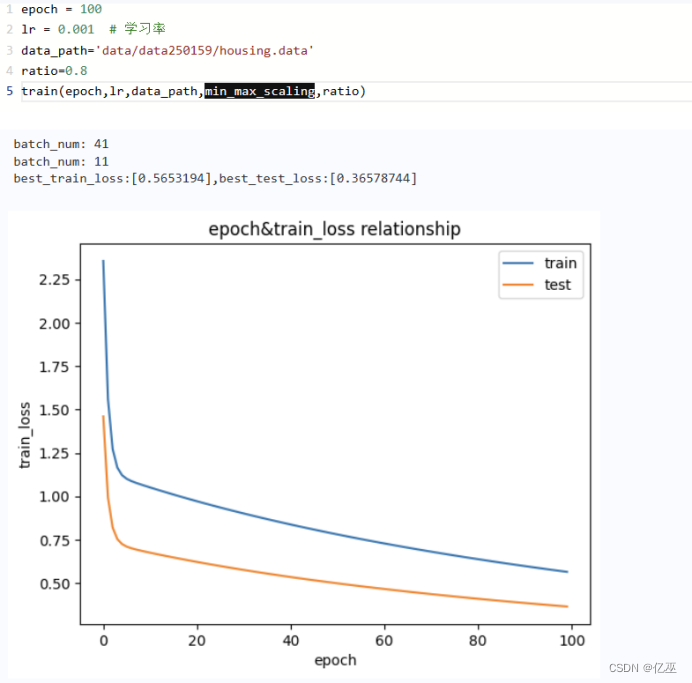
比较发现此数据集用均值归一化在0-10之间比用最大最小归一化收敛更快,迅速下降,下降幅度大
遍历学习率寻找最优
epoch = 100lr = 0.001 # 学习率data_path='data/data250159/housing.data'ratio=0.8t=[]testloss=[]while lr<0.11: a,b=train(epoch,lr,data_path,min_max_scaling,ratio) t.append(a) testloss.append(b) lr=lr+0.002# 找到最小值min_value = min(testloss)# 找到最小值所在的位置min_index = testloss.index(min_value)best_lr=t[min_index]plt.plot(t,testloss, label='lr_loss')# 添加标题和标签plt.title('lr&test_loss relationship')plt.xlabel('lr')plt.ylabel('test_loss')# 显示图例plt.legend()# 显示图表plt.show()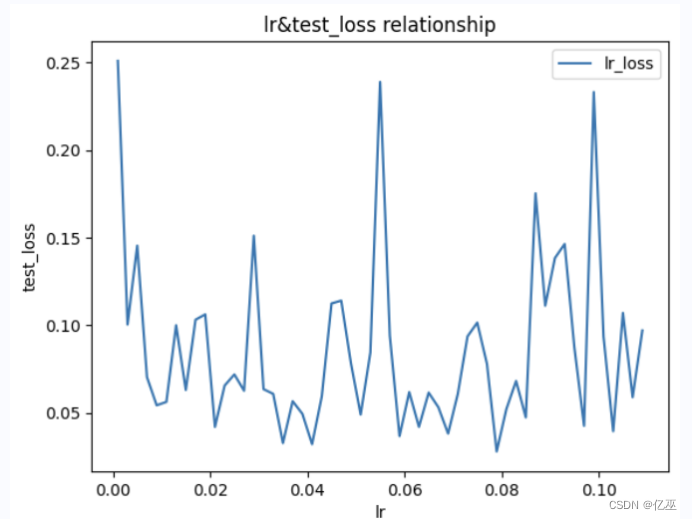
发现随着lr的增大,最佳test_loss可能增大可能减小
得到最佳学习率和最佳test_loss为
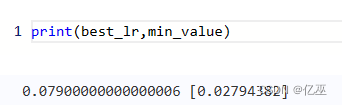
改变数据划分比例
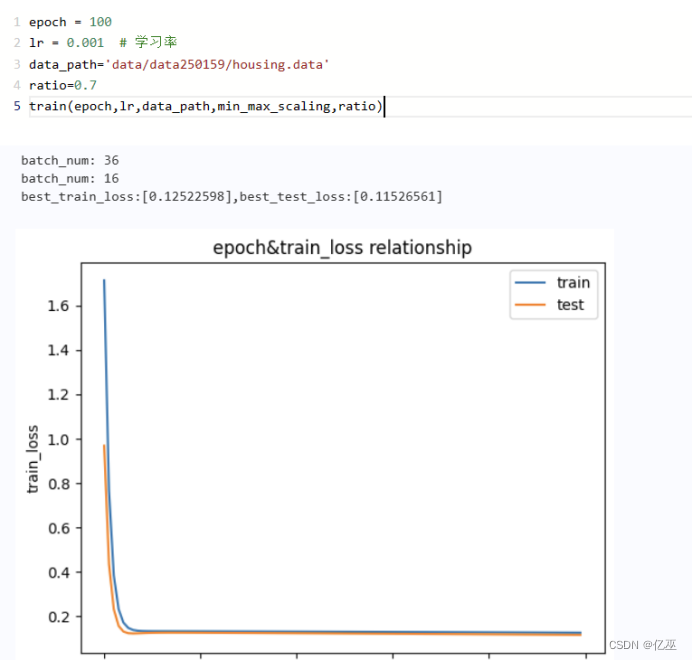
Ratio=0.7
从图上来看,训练损失函数值和测试损失函数值更相近了
五、实验总结与心得体会
在尝试使用shuffle对数据集进行批次乱序的时候发现报错,只要numpy数组可以用shuffle,
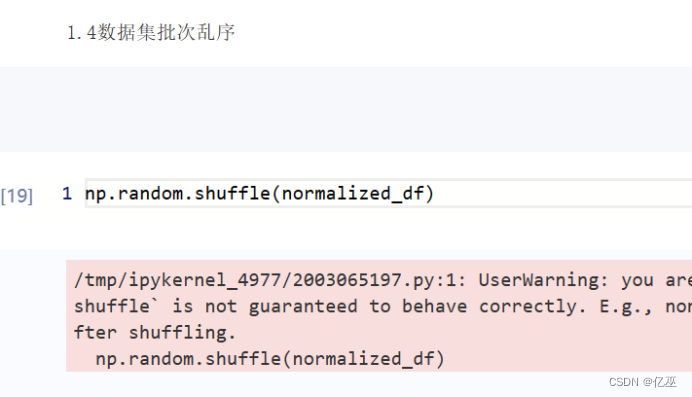
而我的数据类型是dataframe,通过这次搭建单层全连接神经网络,发现实践真的让人对理论理解得更加清晰,出现的报错多数还是因为不同数据类型的理解有些混淆,重新熟悉了一下python的用法,而且相信不管是什么神经网络,都是按照上面所画得流程图来进行得,还想尝试更多的网络构建,因为感觉自己搭一个网路出来会很有成就感。