算法第六期——DFS初入门(深度优先搜索)(Python)
目录
一、蛮力的技术:搜索
1.1、【暴力法】
1.2、蛮力的基本方法——扫描
二、搜索的基本方法
2.1、BFS:一群老鼠走迷宫
2.2、DFS:一只老鼠走迷宫
2.3、BFS和DFS的异同
三、DFS详解
3.1、DFS访问示例
3.2、 DFS基础: 递归和记忆化搜索
3.2.1 递归——斐波那契数列
3.2.2改进递归:记忆化
3.3、DFS的常见操作
四、DFS的代码框架
五、例题:搜索和输出所有路径
5.1、样例分析
5.2、DFS搜索所有路径
5.3、代码展示
六、总结
一、蛮力的技术:搜索
搜索:“暴力法”算法思想的具体实现搜索:“通用”的方法。一个问题,如果比较难,那么先尝试一下搜索,或许能启发出更好的算法。技巧:竞赛时遇到不会的难题,用搜索提交一下,有一部分判题数据很弱,得分了!1.1、【暴力法】
暴力法(Brute force,又译为蛮力法):把所有可能性都列举出来,一 一 验证。简单直接,依靠于计算机强大的计算能力和存储能力。
蛮力法也是一种重要的算法设计技术:(1)、理论上,蛮力法可以解决可计算领域的各种问题
(2)、蛮力法经常用来解决一些较小规模的问题
(3)、对于一些重要的问题蛮力法可以产生一些合理的算法,具备一些实用价值,而且不受问题规模的限制。
(4)、蛮力法可以作为某类问题时间性能的底限(基准),来衡量同样问题的更高效算法
1.2、暴力的基本方法——扫描
关键——依次处理所有元素
基本的扫描技术——遍历
集合的遍历(也可以用前面提到过的用二进制模拟计算)线性表的遍历(数组、链表、队列、栈)树的遍历图的遍历(树是特殊的图)树和图的遍历比较复杂,一般用DFS和BFS来搜索
二、搜索的基本方法
【BFS]】Breadth-First Search,宽度优先搜索,或称为广度优先搜索
【DFS】Depth-First Search,深度优先搜索
2.1、BFS:一群老鼠走迷宫
老鼠无限多;在每个路口,都派出部分老鼠探索所有没走过的路;走某条路的老鼠,如果碰壁无法前行,就停下;如果到达的路口已经有别的老鼠探索过了,也停下;所有的道路都会走到,而且不会重复 。
特点:全面扩散,逐层递进
用途:解决起始点到终点的最短路径((步数)的问题
2.2、DFS:一只老鼠走迷宫
只有一只老鼠;在每个路口,都选择先走右边(当然,选择先走左边也可以),能走多远就走多远;碰壁无法再继续往前走,回退一步,这一次走左边,然后继续往下走;能走遍所有的路,而且不会重复 (回退不算重复) 。
特点:一路到底,逐层回退
用途:解决输出起始点到终点的所有路径的问题
2.3、BFS和DFS的异同
相同点:搜索整个空间 ;
不同点:
DFS:一路往最深的地方走;BFS:一层一层往外扩散
DFS空间占用少,BFS时间效率高
三、DFS详解
3.1、DFS访问示例
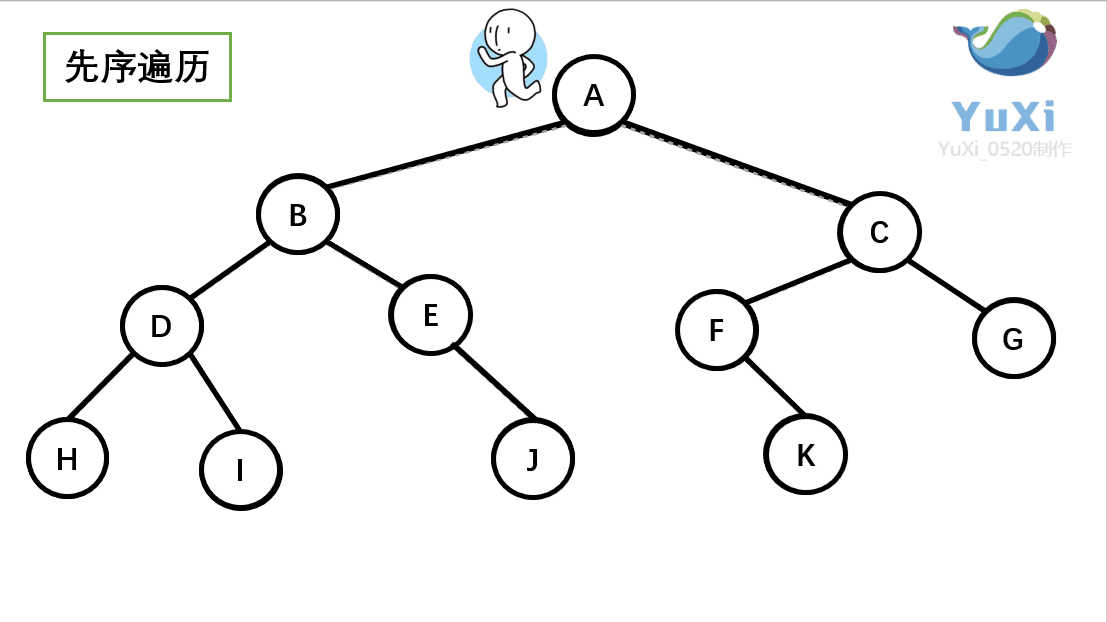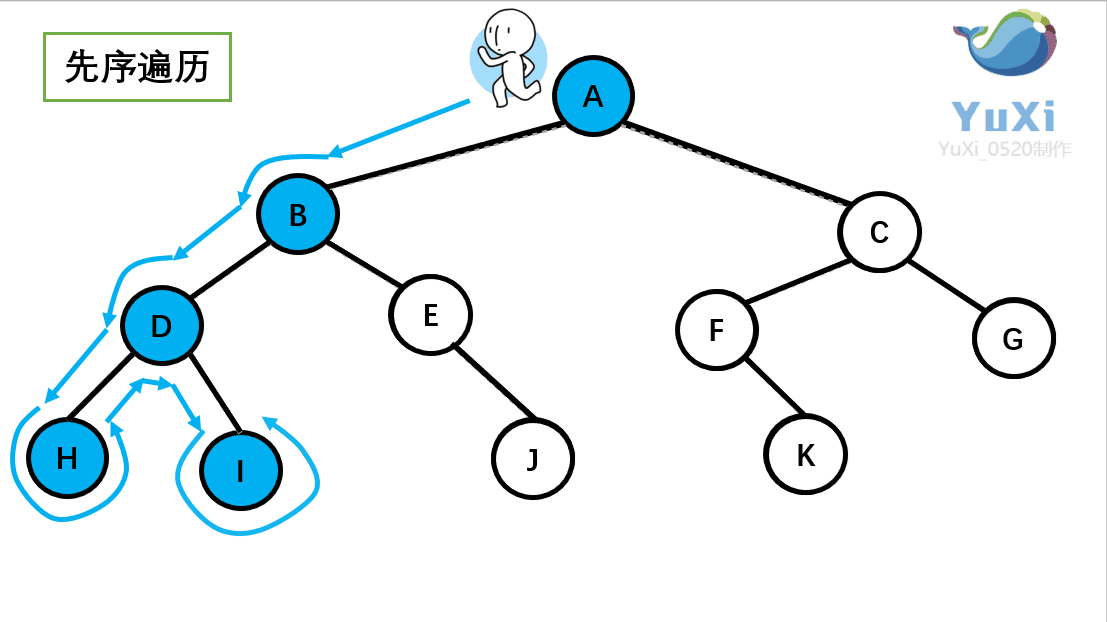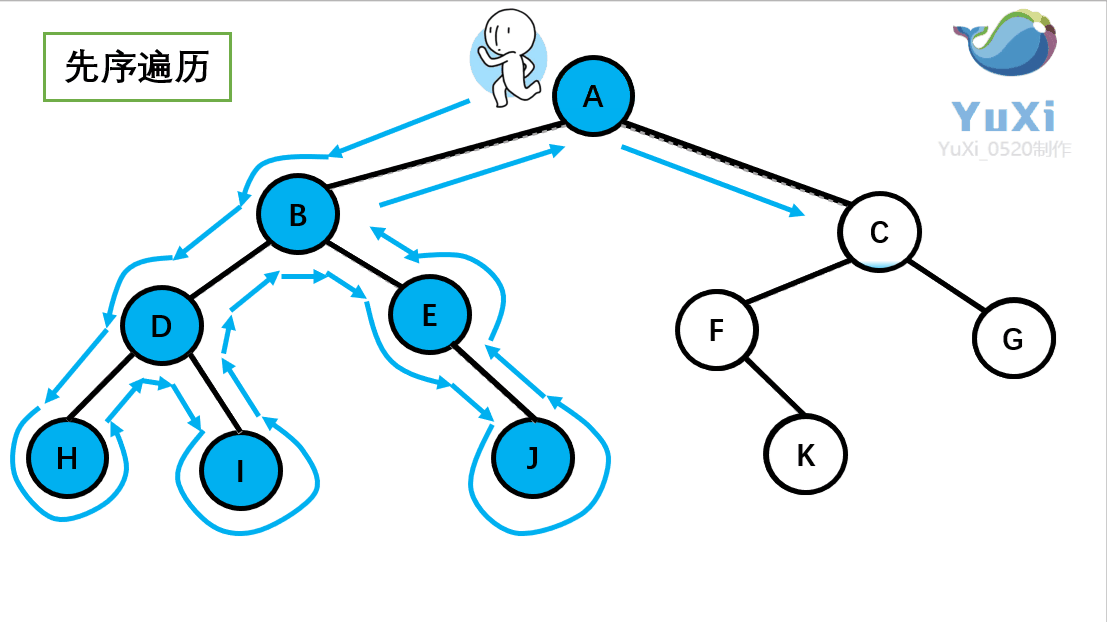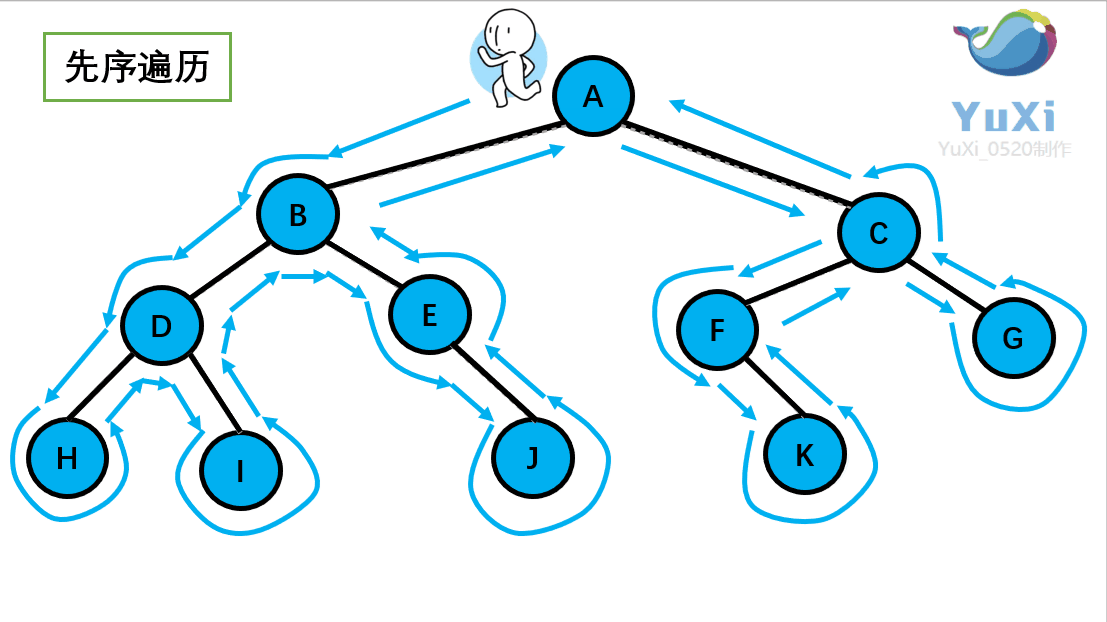
设先访问左节点,后访问右节点;模拟老鼠走迷宫 访问顺序:{ E B A D C G F I H },如下图:补充:如果是BFS的访问就简单多了,访问顺序:E→BG→ADFI→CH(一层一层的访问)
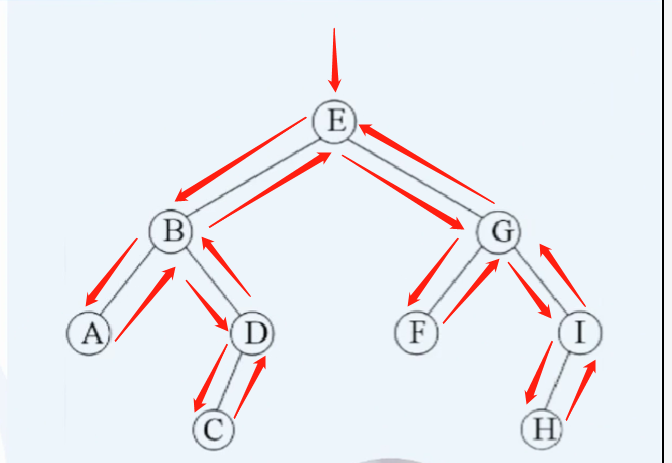
这个访问方式是我们之前讲过的先序遍历 ,我们回顾一下那个小人:沿着外围跑一圈(直到跑回根节点)
3.2、 DFS基础: 递归和记忆化搜索
形式上,递归函数是“自己调用自己”,是一个不断“重复”的过程。
递归有两个过程:递归前进、递归返回(回溯)
①把大问题逐步缩小,直到变成最小的同类问题的过程,而最后的小问题的解是已知的,一般是给定的初始条件。
②到达最小问题后,再“回溯”,把小问题的解逐个带回给更大的问题,最终最大问题也得到了解决。
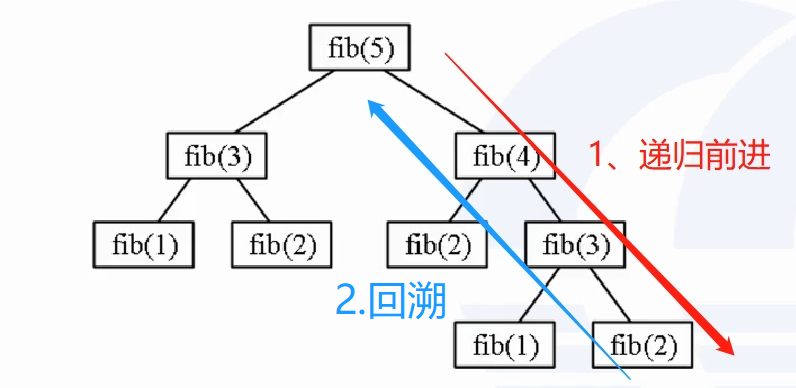
在递归的过程中,由于大问题和小问题的解决方法完全一样,那么大问题的代码和小问题的代码可以写成一样。一个递归函数,直接调用自己,实现了程序的复用。
3.2.1 递归——斐波那契数列
递推式: f(n) = f(n-1) + f(n-2)打印第20个项:
fib=[0]*25fib[1]=1fib[2]=1for i in range(3,21): fib[i]=fib[i-1]+fib[i-2]print(fib[20]) # 6765改用递归来实现
def fib(n): global cnt # 全局变量 cnt += 1 # 统计执行了多少次递归 if n==1 or n==2: # #到达终止条件,即最小问题 return 1 return fib(n-1)+fib(n-2) #递归调用自己2次,复杂度0(2的n次方)cnt =0print(fib(20)) # 6765print(cnt) # 递归了cnt=13529次函数fib(20)计算斐波那契数
递归过程:
到达终止条件: fib(2)= 1,fib(1) = 1
递归返回 (回溯):fib(3) = fib(2) + fib(1) =1+1=2递归返回 (回溯):fib(4) = fib(3) + fib(2) =2+1=3……………………………………………………递归返回 (回溯) :fib(20)=fib(19)+fib(18)=4181+2584=6765提问: 递推和递归两种代码,结果一样,计算量差别巨大?(递推代码:一个for循环,计算20次。递归代码: 计算第20个斐波那契数,共计算cnt = 13529次)
代码低效的原因:
return fib (n-1) + fib (n-2) 递归调用了自己2次,倍增
计算fib(n)时,共执行了O()次递归
不过,很多递归函数只调用自己一次,不会额外增加计算量。
3.2.2改进递归:记忆化
递归的过程中做了重复工作,例如fb(3)计算了2次,其实只算1次就够了。为避免递归时重复计算,可以在子问题得到解决时,就保存结果,再次需要这个结果时,直接返回保存的结果就行了,不继续递归下去这种存储已经解决的子问题结果的技术称为“记忆化”(Memoization) 记忆化是递归的常用优化技术。动态规划也常常用递归写代码,记忆化也是动态规划的关键技术。import syssys.setrecursionlimit(30000) #设置递归深度def fib(n) : global cnt cnt += 1 if n==1 or n==2: data[n]=1 return data[n] if data[n] != 0: # 已经保存过,直接用 return data[n] data[n] = fib(n-1)+fib(n-2) # 没有保存的,计算完后保存到data return data[n]data=[0]*3005 # 存储结果cnt =0print(fib(3000)) # 约等于4*10的626次方print(cnt) # 递归次数,cnt=5997递归的关键问题:递归深度不能太大。Python默认递归深度1000,如果递归深度太大,提示“maximum recursion depth exceeded in comparison”。 可以用sys.setrecursionlimit( )来扩展递归深度,因为常常有深度大于1000的递归题目
3.3、DFS的常见操作
DFS的代码比BFS更简短。
DFS的主要操作:
时间戳
DFS序树深度子树节点数中序输出先序输出后序输出后面三个在之前二叉树部分已经讲过啦!!!
注:这部分在后面文章会详细讲解!
四、DFS的代码框架(重点!!!)
DFS的框架,请在大量编码的基础上,再回头体会这个框架的作用。
ans #答案,用全局变量表示def dfs(层数,其他参数): if 出局判断: #到达最底层,或者满足条件退出(递归结束条件) 更新答案 #答案一般用全局变量表示 return #返回到上一层 剪枝 #在进一步DFS之前剪枝 # DFS主程序 for(枚举下一层可能的情况): # 对每一个情况继续DFS if used[i] == 0: # 如果状态i没有用过,就可以进入下一层 used[i] =1 # 标记状态i,表示已经用过,在更底层不能再使用 dfs(层数+1,其他参数) # 下一层 used[i] = 0 # 恢复状态,从底层状态进行回溯时,不影响上一层对这个状态的使用 return # 返回到上一层DFS:保护现场、恢复现场(记忆化):
第11行的used[i] = 1,称为“保存现场”,或“占有现场”
第13行的used[i] = 0,称为“恢复现场”,或“释放现场”
上面框架可以简写为:
def dfs(): if (): # 搜索结束条件 () # 记录一些结果 return if(): # 剪枝部分 return for next in (): () # 遍历下一层的路径 dfs(next) # 递归下一层 () # 回溯恢复现场DFS函数的要素:
终止条件剪枝(不一定每道题都有):可行性剪枝、重复性剪枝、最优性剪枝递归搜索下一层保存现场和恢复现场五、例题:搜索和输出所有路径
【题目描述】给出一张图,输出从起点到终点的所有路径。
【输入描述】第一行是整数n,m,分别是行数和列数。后面n行,每行m个符号。'@’是起点,’*’是终点,’·’能走,’#’是墙壁不能走。在每一步,都按左-上-右-下的顺序搜索。在样例中,左上角坐标(0,0),起点坐标(1,1),终点坐标(0,2)。1<n, m <7。
【输出描述】输出所有的路径。坐标(i,j)用ij表示,例如坐标(0,2)表示为02。从左到右是i,从上到下是j。
【输入样例】
5 3.#.#@.*.....#.#【输出样例】
from 11 to 021: 11->21->22->12->022: 11->21->22->12->13->03->023: 11->21->22->23->13->03->024: 11->21->22->23->13->12->025:11->12->026: 11->12->22->23->13->03->027:11->12->13->03->02注:这道题需要输出所有路径,但一般比赛题目只要求输出字典序最小的路径。
5.1、样例分析
【第一条路经】
从起点(1,1)出发,查询它的“左-上-右-下”哪个方向能走,发现“左-上”不能走,可以走“右”。第一步走到右边的(2,1)。然后从(2,1)继续走,它可以向上走到(2,0),但是后面就走不通了,退回来改走下面的(2,2)。逐步深入走到终点,最后得到一条从起点(1,1)到终点(0,2)的路径“11->21->22->12->02”。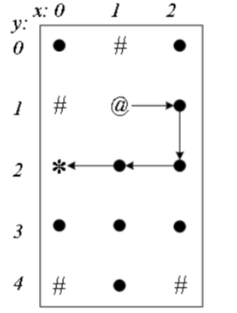
例如上图,当从(2,1)走到(2,2)后,(2,1)被“保护现场”,所有不能再退回(2,1)。
到达终点后,从终点退回,回溯寻找下一个路径。退回后“恢复现场”。例如下图,到达终点后,才可从终点退到(1,2) ,终点(2,0)被“恢复现场”。
【第二条路经】
搜到一条路径后,从终点(0,2)退回到(1,2),继续走到(1,3)、(0,3)、(0,2)。
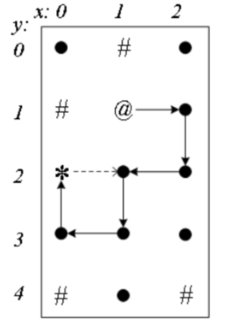
退回到(1,2)后,往上,往右都被“保护现场”,只能往下走到(1,3) ,再往左到(0,3),往左走不通,往上到终点。
【第三条路经】
从终点(0,2)一路退回到(2,2)后,才找到新路径。在退回的过程中,原来被“保存现场的”(0,3)、(1,3)、(0,2),重新被“恢复现场”,允许被经过。例如(1,3),在第二条路径中曾用过,这次再搜新路径时,在第三条路径中重新经过了它。如果不“恢复现场”,这个点就不能在新路径中重新用了。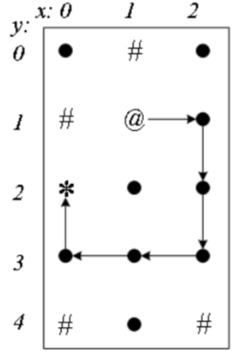
【第四条路径】
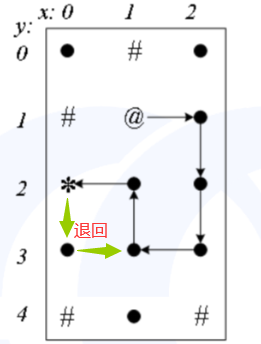
5.2、DFS搜索所有路径
“保存现场”的作用:禁止重复使用。当搜索一条从起点到终点的路径时,这条路径上经过的点,不能重复经过,否则就兜圈子了,所以路径上的点需要“保存现场”,禁止再经过它。没有经过的点,或者碰壁后退回的点,都不能“保存现场”,这些点可能后面会进入这条路径。
“恢复现场”的作用:当重新搜新的路径时,方法是从终点(或碰壁的点) 沿着旧路径逐步退回,每退回一个点,就对这个点“恢复现场”,允许新路径重新经过这个点。
5.3、代码展示
路径有很多条,需要记录每条路径然后打印,这个代码使用了“输出最短路径的简单方法”:每到一个点,就在这个点上记录从起点到这个点的路径。 p[ ][ ]记录路径,p[ i ][ j ]用字符串记录了从起点到点(i,j)的完整路径。第14行把新的点(nx,ny)加入到这个路径。这种方法浪费空间,适用于小图。def dfs(x, y): global num for i in range(0, 4): # 每次搜索有四个方向可以选择 dir = [(-1, 0), (0, -1), (1, 0), (0, 1)] # 四个方向左、上、右、下 nx, ny = x + dir[i][0], y + dir[i][1] # 新坐标 if nx < 0 or nx >= hx or ny < 0 or ny > wy: # 判断出局:不在地图内 continue # 换个方向,继续找下一个路径 if mp[nx][ny]== '*': # 到达终点一次 num += 1 print("%d:%s->%d%d" % (num, p[x][y], nx, ny)) # 打印路径:起点到上一个点的路径->终点 continue # 换个方向,继续找下一个路径 if mp[nx][ny]== ".": # 可以走的路 mp[nx][ny]="#" # 保存现场(用#表示)。这个点在这次更深的dfs中不能再用 p[nx][ny] = p[x][y] + '->' + str(nx) + str(ny) # 记录路径:起点到上一个点的路径——>下一个点 dfs(nx, ny) mp[nx][ny] = '.' # 恢复现场。回溯之后,这个点可以再次用num = 0 # 统计路径个数wy, hx = map(int, input().split()) #Wy行,Hx列。a = [""] * 10 # 用来保存迷宫for i in range(wy): # 读迷宫,每次读一行 a[i] = list(input())mp = [[' '] * 10 for i in range(10)] #二维矩阵mp[][]表示迷宫# 把a存到mp中(x,y颠倒,因为第一维坐标是y,第二维坐标是x);找到起点和终点for x in range(hx): for y in range(wy): mp[x][y] = a[y][x] if mp[x][y] == '@': sx = x; sy = y # 起点 if mp[x][y] == "*": tx = x; ty = y # 终点print("from %d%d to %d%d" % (sx, sy, tx, ty))p = [[''] * 10 for i in range(10)] # 记录从起点到点path[i][i]的路径p[sx][sy] = str(sx) + str(sy) # 把起点存进路劲dfs(sx, sy) # 从起点开始搜索并输出所有的路径六、总结
搜所有的路径,应该用DFS;如果只搜最短路径,应该用BFS。在一张图上,从起点到终点的所有路径数量是一个天文数字,读者可以用上面的代码试试一个8x8的图,看看路径总数是多少。但是搜最短的路径就比较简单,并不需要把所有路径搜出来之后再比较得到最短路。用BFS可以极快地搜到最短路。DFS适合用来处理暴力搜所有情况的题目。
本文参考罗勇军老师的蓝桥云课

登录后可发表评论
点击登录