2021级浴帘实验
本文只涉及功能实现的思路，针对期末复习，不涉及制作操作界面。
C++单词拼装器
实验内容
1. 把C++源代码中的各类单词（记号）进行拼装分类。
C++语言包含了几种类型的单词（记号）：标识符，关键字，数（包括整数、浮点数），字符串、注释、特殊符号（分界符）和运算符号等【详细的单词类别及拼装规则见另外的文件说明】。
2. 打开一个C++源文件，列出所有可以拼装的单词（记号）。
最后呈现的内容：
# 特殊符号
20.26 数字
-21.567 数字
abc123 标识符
_ad 标识符
if 关键字
实验思路
实现这个拼装器，就会想到正则表达式。
为什么会涉及到正则表达式？
我们知道，要实现拼装器的功能，需要识别关键字，特殊符号，运算符号，这三类是C++完全规定好的，比较好识别，我称其为简三类。
另外三类我称其为难三类，它们是标识符，数，注释，这三类C++只是给了一个书写规则，并没有具体规定它是什么，这个时候，我们就要用到正则表达式去匹配这三类，看它们是否符合书写规则。
C++单词拼装器可以看作是词法分析器的一个前导实验，因为此时DFA和NFA还没学利索，所以还不能用正则表达式来匹配难三类（真正的词法分析需要：正则表达式-->NFA--->DFA-->DFA最小化-->词法分析），故本实验暂时用if-else if-else来枚举各种情况。
代码
1、首先要考虑的是文件操作。
#include <fstream>#include <iostream>#include <string>#include <set>#include <vector>#include <cctype>#include <sstream>using namespace std;int main() { ifstream file("filename.txt"); //把filename处改为你要读的file if (!file) {//若文件打开失败，返回错误 cout << "Unable to open file"; exit(1); } //将文件内容读到字符串fileContent里 string fileContent((istreambuf_iterator<char>(file)), istreambuf_iterator<char>()); ........ return 0;}2、需要逐行逐个读输入，如果当前读到的不符合当前类型，保存并回退一个字符。
比如说：我现在正在处理的串为：22.04 + 23.88，现在我的currentToken里有22.04，当前类型为digit，继续往后读，读到了‘+’，‘+’类型为symbol，所以digit结束并保存currentToken到resultToken中，别忘记把‘+’放回去，等待下一轮的读取。
第一步：实现逐行处理，写一个split函数，它的功能是输入一串字符，把这串字符逐行切割，并将切割结果逐行存储在tokens里，返回tokens。
vector<string> split(const string &s, char delimiter) {//delimiter为切割这个串的字符 vector<string> tokens; string token; istringstream tokenStream(s); while (getline(tokenStream, token, delimiter)) { tokens.push_back(token); } return tokens;}第二步：实现逐个处理
void Wordassembly(string fileContent) { ............. vector<string> lines = split(fileContent, '\n');//返回切好的tokens string resultText;//用来存储处理结果 for (string &line: lines){//逐行处理 string currentToken; ......... for (int i = 0; i < line.length(); ++i) {//逐个处理 char currentChar = line[i]; ........... } }}第三步：如果当前读到的不符合当前类型，保存并回退一个字符。
目前程序的实现方式是：读我要分析的文件，将它保存在fileContent里 -> 用自己写的split函数逐行切割fileContent，以便实现逐行处理 -> 逐行逐个处理
⚠️为防止对部分代码产生疑惑，此处为代码逐个字符处理逻辑的简述：
本代码中实现的逻辑是，currentToken先读一个line[i]进去，然后再判断currentToken究竟与什么匹配，在每个尝试匹配的函数中，都会从line[i]开始向后枚举(i++)，逐个被currentToken接收，直到line[i]不是当前类型的字符，所以在进入时我们需要清空currentToken，防止line[i]被接收两次。
比如说：currentToken读了一个line[0] = '1'进去，进入匹配流程，匹配到它是一个数字，所以进入处理数字的函数，此时i = 0，此时currenToken = "1"。
因为这个数字可能是1，也可能是123313，所以我们需要不停往后看（i++），边看currentToken边接收当前字符，直到当前字符不是一个数字为止。
我的逻辑是从i开始看，在本例中，就是从i = 0开始看。所以我需要在开始看之前，先清空已经记录下line[0]的currenToken，防止它读入两次line[0]。
我们注意到，逻辑需要i++到直到当前字符不是一个数字为止，当前字符虽然不是一个数字，我们也不能把它丢掉，所以在每次匹配后我们还要把不是当前类型的当前字符塞回去（i--），再进行下一轮的匹配。
例：
void process_digit(string& currentToken, int& i ,string& line);void Wordassembly(string fileContent) { ............. vector<string> lines = split(fileContent, '\n');//返回切好的tokens string resultText;//用来存储处理结果 for (string &line: lines){//逐行处理 string currentToken;//记录识别完成的字符 ......... for (int i = 0; i < line.length(); ++i) {//逐个处理 currentToken += line[i];//我们目前在看的字符 if(currentToken 是dight类型){ process_digit(currentToken, i , line); continue; } ........... } }}void process_digit(string& currentToken, int& i ,string& line){ currentToken.clear();//倒掉 for(; i < line.size(); i++){ ......... if(line[i]不是digit){ break; } } resultText += currentToken + "数字\n"; currentToken.clear();//清空currentToken i--;//回退一个字符}3、简三类的处理
第一步：将可以识别的简三类分别放在set里，set作为全局变量
set<string> keywords = { "asm", "auto", "bool", "break", "case", "catch", "char", "class", "const", "continue", "default", "delete", "do", "double", "else", "enum", "except", "explicit", "extern", "false", "finally", "float", "for", "friend", "goto", "if", "inline", "int", "long", "mutable", "namespace", "new", "operator", "private", "protected", "public", "register", "return", "short", "signed", "sizeof", "static", "struct", "string", "switch", "template", "this", "throw", "true", "try", "typedef", "typename", "union", "unsigned", "using", "virtual", "void", "while", "main", "std", "cin", "cout", "endl", "scanf", "printf", "include", "define", "iostream.h", "iostream", "stdio.h" };set<string> symbols = { "$", "&", "_", "#", "<", "<=", "=", ">", ">=", "<>", "<<", "==", "!=", "&&", "||", "!", ";", ".", "(", ")", "{", "}", ">>", "()"};set<string> operate = { "+", "-", "*", "/", "++", "--", "^", "|", "%" };第二步：开始处理，找set里有没有对应的简三类（第一个读到的是字母，找keywords里有没有，第一个读到的是符号，找symbols/operate里有没有），如果有，保存结果。
void Wordassembly(string fileContent) { vector<string> lines = split(fileContent, '\n'); string resultText;//保存结果 for (string &line: lines) { string currentToken; for (int i = 0; i < line.length(); ++i) { char currentChar = line[i]; process_Token_keywords(currentToken, keywords, resultText);//处理keywords process_Token_op_or_sym(currentToken, symbols, operate, resultText);//处理符号和运算符 }}//处理keywordbool isKeyword(const string& token, const set<string>& keywords) { return keywords.find(token) != keywords.end();}void process_Token_keywords(string& currentToken, const set<string>& keywords, string& resultText) { if (!currentToken.empty()) { if (isKeyword(currentToken, keywords)) {//如果找到了keyword resultText += currentToken + " 关键字\n"; currentToken.clear(); } }}//处理运算符和其他符号bool isSymbol(const string& token, const set<string>& symbols) { return symbols.find(token) != symbols.end();}bool isOperator(const string& token, const set<string>& operators) { return operators.find(token) != operators.end();}void process_Token_op_or_sym(string& currentToken, int& i, string& line, const set<string>& op, const set<string> &sym, string &resultText){ if(isSymbol(currentToken, sym)){//在symbols里找到了 //对两个符号的特殊处理 if(currentToken == "<"){//列举<开头的特殊符号 if(i + 1 < line.size() && (line[i + 1] == '>'||line[i + 1] == '<'||line[i + 1] == '=')){ currentToken += line[i + 1]; resultText += currentToken + "特殊符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + "特殊符号\n"; currentToken.clear(); } } else if(currentToken == ">"){//列举>开头的特殊符号 if(i + 1 < line.size() && (line[i + 1] == '>'||line[i + 1] == '=')){ currentToken += line[i + 1]; resultText += currentToken + "特殊符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + "特殊符号\n"; currentToken.clear(); } } else if(currentToken == "="){//列举=开头的特殊符号 if(i + 1 < line.size() && (line[i + 1] == '=')){ currentToken += line[i + 1]; resultText += currentToken + "特殊符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + "运算符号\n";//这里比较特殊，请注意 currentToken.clear(); } } else if(currentToken == "!"){//列举!开头的特殊符号 if(i + 1 < line.size() && (line[i + 1] == '=')){ currentToken += line[i + 1]; resultText += currentToken + "特殊符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + "特殊符号\n"; currentToken.clear(); } } else if(currentToken == "&"){//列举!开头的特殊符号 if(i + 1 < line.size() && (line[i + 1] == '&')){ currentToken += line[i + 1]; resultText += currentToken + "特殊符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + "特殊符号\n"; currentToken.clear(); } } else if(currentToken == "|"){//列举!开头的特殊符号 if(i + 1 < line.size() && (line[i + 1] == '|')){ currentToken += line[i + 1]; resultText += currentToken + "特殊符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + "特殊符号\n"; currentToken.clear(); } } else{ resultText += currentToken + "特殊符号\n"; currentToken.clear();} }//end if else if(isOperator(currentToken, op)){//在operator里找到了 //对包含两个符号的特殊处理 if(currentToken == "+"){ if(i + 1 < line.size() && (line[i + 1] == '+')){ currentToken += line[i + 1]; resultText += currentToken + "运算符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + "运算符号\n"; currentToken.clear(); } } else if(currentToken == "-"){ if(i + 1 < line.size() && (line[i + 1] == '-')){ currentToken += line[i + 1]; resultText += currentToken + "运算符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + "运算符号\n"; currentToken.clear(); } } else{ resultText += currentToken + "运算符号\n"; currentToken.clear();} }//end else-if}上述代码只是看起来多，核心思想就是：当我读到一个字符时，比如我读到了‘+’，它此时已经可以与operator匹配了，但我们要想到，它也可能是‘++’，所以我们需要枚举由两个符号组成的符号的情况，以完成正确的匹配。
4、简三类处理完毕，随后处理难三类
在正式开始处理前，需要考虑空格的问题，也就是说，我们分析的这串程序，也可以以空格作为不同类型的切分，比如说int a，它用空格把keyword和标识符分开了。
所以我们可以加入isblank()的处理，它的作用是：分离两个不同的类型，并忽略无意义的空格。
空格包括： '\f', '\r', '\t', '\v'。
在isblank里，需要先把currentToken清空一次，因为在本程序的逻辑里，currentToken在输入到isblank函数里之前，就已经获得了line[i]，若这个line[i]是一个空格，我们就需要把currentToken里的空格给倒掉，防止影响后续程序的判断。
bool isblank(string& currentToken, int& i, string& line){ //是空格 if(i < line.size() && (line[i] == ' ' || line[i] == '\t' || line[i] == '\n' || line[i] == '\r' || line[i] == '\f' || line[i] == '\v')){ currentToken.clear();//倒掉空格 while(i < line.size() && (line[i] == ' ' || line[i] == '\t' || line[i] == '\n' || line[i] == '\r' || line[i] == '\f' || line[i] == '\v')){//跳过多个空格 i++; } i--; return true;//表示有空格，且分离完成 } //不是空格 return false;}处理注释：此处分为单行和多行
我们发现，注释的识别与运算符识别有重合，所以我们需要在运算符识别里添加处理注释的情况，字符串的识别与特殊符号识别有重合，所以我们需要在特殊符号识别里添加处理注释的情况。
void process_Token_op_or_sym(string& currentToken, int& i, string& line, const set<string>& op, const set<string> &sym, string &resultText){ bool isComment = false;//可能匹配到注释符号 ........ if(isSymbol(currentToken, sym)){//在symbols里找到了 ...... else if(currentToken == "\""){//处理string currentToken.clear(); if(i + 1 < line.size()){//跳过前面的” i++; } while(i < line.size() && line[i] != '"'){ currentToken += line[i]; i++; } if(i + 1 < line.size()){//跳过后面的“ i++; } resultText += currentToken + "字符串\n"; } ...... } else if(isOperator(currentToken, op)){//在operator里找到了 ...... else if(currentToken == "/"){ if(i + 1 < line.size() && (line[i + 1] == '/' || line[i + 1] == '*')){//处理注释的情况 isComment = true; } else{ resultText += currentToken + "运算符号\n"; currentToken.clear(); } } ....... }//end else-if}string处理完毕，接下来要处理注释
bool isComment(string& currentToken){ if(currentToken == "//" || currentToken == "/*"){ return true; } return false;}void process_Comment(string& currentToken, int& i, string& line, string& resultText){ currentToken.clear();//因为我不需要显示注释符 bool is_break = false; if(i + 1 < line.size()){//跳过当前字符 i++; } for(;i < line.size(); i++){ if(line[i] == '*'){ if(i + 1 < line.size() && line[i] == '/'){ resultText += currentToken + "注释\n"; currentToken.clear(); is_break = true; break; } } currentToken += line[i]; } if(!is_break){ resultText += currentToken + "注释\n"; currentToken.clear(); } }处理数字：数字有浮点数，正负号，0x，指数（e, E）
我们注意到，需要处理标识符中有数字的情况。
// 检查是否为数字或正负号bool isdigit(const string& currentToken){ if(currentToken.empty()) return false; char firstChar = currentToken[0]; return std::isdigit(firstChar);}// 处理数字void process_digit(string& currentToken, int& i, const string& line, string& resultText){ bool is_alpha = false; i++;//因为currentToken已经获得了line[i] while(i < line.length() && (std::isdigit(line[i]) || line[i] == '.' || line[i] == 'e' || line[i] == 'E' || line[i] == '-' || line[i] == '+' ||(line[i - 1] == '0' && (line[i] == 'x' || line[i] == 'X')))) { //先处理0x的情况 if(line[i - 1] == '0' && (line[i] == 'x' || line[i] == 'X')){//吃掉0x currentToken += line[i]; i++; } // 如果遇到可能是标识符的字符，停止处理数字 if (isalpha(line[i]) && line[i] != 'e' && line[i] != 'E') { is_alpha = true; break; } if(i + 1 < line.size() && line[i + 1] == '_'){ is_alpha = true; break; } currentToken += line[i]; i++; }//end while i--; if(is_alpha == false){ resultText += currentToken + " 数字\n"; currentToken.clear(); }}处理标识符
如果currentToken第一个是字母或者下划线，它就有可能是标识符，我们注意到，关键字属于标识符，所以把关键字处理也放到标识符处理中。
注意，我们需要让keyword遵守最长匹配原则，实现最长匹配原则，程序需要在遇到一个可能的关键字时继续向前查看，直到确定没有更长的匹配可能。
比如说double，不要匹配成do 关键字 uble 标识符
//识别标识符，把处理keyword放在处理标识符的里面bool issigned(const string& currentToken){ if(currentToken.empty()) return false; char firstChar = currentToken[0]; return std::isalpha(firstChar) || firstChar == '_';}//处理标识符void process_signed(string& currentToken, int& i, const string& line, string& resultText){ string longestMatch; currentToken.clear();//同样是因为currentToken已经提前读入了一个用于判断，所以我们要把它倒回去 string tempToken = currentToken; int tempIndex = i; while(tempIndex < line.length() && (std::isdigit(line[tempIndex]) || std::isalpha(line[tempIndex]) || line[tempIndex] == '_')) { tempToken += line[tempIndex]; if(isKeyword(tempToken, keywords)){ longestMatch = tempToken; } tempIndex++; } if(!longestMatch.empty()){ resultText += longestMatch + " 关键字\n"; currentToken.clear(); i = --tempIndex;//回退一个字符 } else { while(i < line.length() && (std::isdigit(line[i]) || std::isalpha(line[i]) || line[i] == '_')) { currentToken += line[i]; i++; } i--;//回退一个字符 resultText += currentToken + " 标识符\n"; currentToken.clear(); }}调用写好的所有功能
//调用所有写好的函数void Wordassembly(string fileContent) { vector<string> lines = split(fileContent, '\n'); string resultText; for (string &line: lines) { string currentToken; currentToken.clear(); for (int i = 0; i < line.length(); i++) { currentToken += line[i]; //处理符号 if(!currentToken.empty()){ if(isSymbol(currentToken, symbols)||isOperator(currentToken, operators)){ process_Token_op_or_sym(currentToken, i, line, operators, symbols, resultText); } //处理空格 if (isblank(currentToken, i, line)) { continue; } // 处理注释 if (isComment(currentToken)) { process_Comment(currentToken, i, line, resultText); continue; } //处理数字 if (isdigit(currentToken)) { process_digit(currentToken, i, line, resultText); continue; } // 首先尝试将token识别为标识符 if (issigned(currentToken)) { process_signed(currentToken, i, line, resultText); continue; } } } } // 输出结果 cout << resultText << endl;}最终程序
#include <iostream>#include <string>#include <set>#include <vector>#include <cctype>#include <sstream>#include <fstream>using namespace std;set<string> keywords = { "asm", "auto", "bool", "break", "case", "catch", "char", "class", "const", "continue", "default", "delete", "do", "double", "else", "enum", "except", "explicit", "extern", "false", "finally", "float", "for", "friend", "goto", "if", "inline", "int", "long", "mutable", "namespace", "new", "operator", "private", "protected", "public", "register", "return", "short", "signed", "sizeof", "static", "struct", "string", "switch", "template", "this", "throw", "true", "try", "typedef", "typename", "union", "unsigned", "using", "virtual", "void", "while", "main", "std", "cin", "cout", "endl", "scanf", "printf", "include", "define", "iostream.h", "iostream", "stdio.h"};set<string> symbols = { "$", "&", "|", "#", "<", "<=", "=", ">", ">=", "<>", "<<", "==", "!=", "&&", "||", "!", ";", ".", "(", ")", "{", "}", ">>"};set<string> operators = { "+", "-", "*", "/", "++", "--", "^", "|", "%" };vector<string> split(const string &s, char delimiter) { vector<string> tokens; string token; istringstream tokenStream(s); while (getline(tokenStream, token, delimiter)) { tokens.push_back(token); } return tokens;}//处理简三类bool isKeyword(const string& token, const set<string>& keywords) { return keywords.find(token) != keywords.end();}bool isSymbol(const string& token, const set<string>& symbols) { return symbols.find(token) != symbols.end();}bool isOperator(const string& token, const set<string>& operators) { return operators.find(token) != operators.end();}void process_Token_keywords(string& currentToken, const set<string>& keywords, string& resultText) { if (!currentToken.empty()) { if (isKeyword(currentToken, keywords)) { resultText += currentToken + " 关键字\n"; currentToken.clear(); } }}void process_Token_op_or_sym(string& currentToken, int& i, string& line, const set<string>& op, const set<string> &sym, string &resultText){ bool isComment = false;//可能匹配到注释符号 if(isSymbol(currentToken, sym)){//在symbols里找到了 //对两个符号的特殊处理 if(currentToken[0] == '<'){//列举<开头的特殊符号 if(i + 1 < line.size() && (line[i + 1] == '>'||line[i + 1] == '<'||line[i + 1] == '=')){ currentToken += line[i + 1]; resultText += currentToken + " 特殊符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + " 特殊符号\n"; currentToken.clear(); } } else if(currentToken[0] == '>'){//列举>开头的特殊符号 if(i + 1 < line.size() && (line[i + 1] == '>'||line[i + 1] == '=')){ currentToken += line[i + 1]; resultText += currentToken + " 特殊符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + " 特殊符号\n"; currentToken.clear(); } } else if(currentToken[0] == '='){//列举=开头的特殊符号 if(i + 1 < line.size() && (line[i + 1] == '=')){ currentToken += line[i + 1]; resultText += currentToken + " 特殊符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + " 运算符号\n";//这里比较特殊，请注意 currentToken.clear(); } } else if(currentToken[0] == '!'){//列举!开头的特殊符号 if(i + 1 < line.size() && (line[i + 1] == '=')){ currentToken += line[i + 1]; resultText += currentToken + " 特殊符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + " 特殊符号\n"; currentToken.clear(); } } else if(currentToken[0] == '&'){//列举!开头的特殊符号 if(i + 1 < line.size() && (line[i + 1] == '&')){ currentToken += line[i + 1]; resultText += currentToken + " 特殊符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + " 特殊符号\n"; currentToken.clear(); } } else if(currentToken[0] == '|'){//列举!开头的特殊符号 if(i + 1 < line.size() && (line[i + 1] == '|')){ currentToken += line[i + 1]; resultText += currentToken + " 特殊符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + " 特殊符号\n"; currentToken.clear(); } } else if(currentToken[0] == '\"'){//处理string currentToken.clear(); if(i + 1 < line.size()){//跳过前面的” i++; } while(i < line.size() && line[i] != '"'){ currentToken += line[i]; i++; } if(i + 1 < line.size()){//跳过后面的“ i++; } resultText += currentToken + " 字符串\n"; currentToken.clear(); } else{ resultText += currentToken + " 特殊符号\n"; currentToken.clear(); } }//end if else if(isOperator(currentToken, op)){//在operator里找到了 //对包含两个符号的特殊处理 if(currentToken[0] == '+'){ if(i + 1 < line.size() && (line[i + 1] == '+')){ currentToken += line[i + 1]; resultText += currentToken + " 运算符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + " 运算符号\n"; currentToken.clear(); } } else if(currentToken[0] == '-'){ if(i + 1 < line.size() && (line[i + 1] == '-')){ currentToken += line[i + 1]; resultText += currentToken + " 运算符号\n"; i++;//表示往前多读了一个 currentToken.clear(); } else{ resultText += currentToken + " 运算符号\n"; currentToken.clear(); } } else if(currentToken[0] == '/'){ if(i + 1 < line.size() && (line[i + 1] == '/' || line[i + 1] == '*')){//处理注释的情况 isComment = true; } else{ resultText += currentToken + " 运算符号\n"; currentToken.clear(); } } else{ resultText += currentToken + " 运算符号\n"; currentToken.clear(); } }//end else-if}bool isblank(string& currentToken, int& i, string& line){ //是空格 if(i < line.size() && (line[i] == ' ' || line[i] == '\t' || line[i] == '\n' || line[i] == '\r' || line[i] == '\f' || line[i] == '\v')){ currentToken.clear(); while(i < line.size() && (line[i] == ' ' || line[i] == '\t' || line[i] == '\n' || line[i] == '\r' || line[i] == '\f' || line[i] == '\v')){//跳过多个空格 i++; } i--; return true;//表示有空格，且分离完成 } //不是空格 return false;}//处理注释bool isComment(string& currentToken){ if(currentToken == "//" || currentToken == "/*"){ return true; } return false;}void process_Comment(string& currentToken, int& i, string& line, string& resultText){ currentToken.clear();//因为我不需要显示注释符 bool is_break = false; if(i + 1 < line.size()){//跳过当前字符 i++; } for(;i < line.size(); i++){ if(line[i] == '*'){ if(i + 1 < line.size() && line[i + 1] == '/'){ resultText += currentToken + "注释\n"; i++; currentToken.clear(); is_break = true; break; } } currentToken += line[i]; } if(!is_break){ resultText += currentToken + "注释\n"; currentToken.clear(); } }// 检查是否为数字或正负号bool isdigit(const string& currentToken){ if(currentToken.empty()) return false; char firstChar = currentToken[0]; return std::isdigit(firstChar);}// 处理数字void process_digit(string& currentToken, int& i, const string& line, string& resultText){ bool is_alpha = false; i++;//因为currentToken已经获得了line[i] while(i < line.length() && (std::isdigit(line[i]) || line[i] == '.' || line[i] == 'e' || line[i] == 'E' || line[i] == '-' || line[i] == '+' ||(line[i - 1] == '0' && (line[i] == 'x' || line[i] == 'X')))) { //先处理0x的情况 if(line[i - 1] == '0' && (line[i] == 'x' || line[i] == 'X')){//吃掉0x currentToken += line[i]; i++; } // 如果遇到可能是标识符的字符，停止处理数字 if (isalpha(line[i]) && line[i] != 'e' && line[i] != 'E') { is_alpha = true; break; } if(i + 1 < line.size() && line[i + 1] == '_'){ is_alpha = true; break; } currentToken += line[i]; i++; }//end while i--; if(is_alpha == false){ resultText += currentToken + " 数字\n"; currentToken.clear(); }}//识别标识符，把处理keyword放在处理标识符的里面bool issigned(const string& currentToken){ if(currentToken.empty()) return false; char firstChar = currentToken[0]; return std::isalpha(firstChar) || firstChar == '_';}//处理标识符void process_signed(string& currentToken, int& i, const string& line, string& resultText){ string longestMatch; currentToken.clear();//同样是因为currentToken已经提前读入了一个用于判断，所以我们要把它倒回去 string tempToken = currentToken; int tempIndex = i; while(tempIndex < line.length() && (std::isdigit(line[tempIndex]) || std::isalpha(line[tempIndex]) || line[tempIndex] == '_')) { tempToken += line[tempIndex]; if(isKeyword(tempToken, keywords)){ longestMatch = tempToken; } tempIndex++; } if(!longestMatch.empty()){ resultText += longestMatch + " 关键字\n"; currentToken.clear(); i = --tempIndex;//回退一个字符 } else { while(i < line.length() && (std::isdigit(line[i]) || std::isalpha(line[i]) || line[i] == '_')) { currentToken += line[i]; i++; } i--;//回退一个字符 resultText += currentToken + " 标识符\n"; currentToken.clear(); }}//调用所有写好的函数void Wordassembly(string fileContent) { vector<string> lines = split(fileContent, '\n'); string resultText; for (string &line: lines) { string currentToken; currentToken.clear(); for (int i = 0; i < line.length(); i++) { currentToken += line[i]; //处理符号 if(!currentToken.empty()){ if(isSymbol(currentToken, symbols)||isOperator(currentToken, operators)){ process_Token_op_or_sym(currentToken, i, line, operators, symbols, resultText); } //处理空格 if (isblank(currentToken, i, line)) { continue; } // 处理注释 if (isComment(currentToken)) { process_Comment(currentToken, i, line, resultText); continue; } //处理数字 if (isdigit(currentToken)) { process_digit(currentToken, i, line, resultText); continue; } // 首先尝试将token识别为标识符 if (issigned(currentToken)) { process_signed(currentToken, i, line, resultText); continue; } } } } // 输出结果 cout << resultText << endl;}int main(int argc, const char * argv[]) { // 打开文件 ifstream file("/Users/chaixichi/Desktop/学习资料/大三上/C++lab1/C++lab1/test.cpp"); //将文件名替换为打开的文件路径 // 查看是否可以打开文件 if (!file) { cout << "Unable to open file"; exit(1); } //将文件中读到的字符串存入fileContent string fileContent((istreambuf_iterator<char>(file)), istreambuf_iterator<char>());// //测试split// vector<string>test = split(fileContent, '\n');// for(int i = 0; i < test.size() ;i++){// cout<<test[i]<<endl;// } Wordassembly(fileContent); return 0;}执行结果
这玩意主要是抠细节比较烦，实现原理还是蛮简单的，就是读完文件后，逐个字符遍历，暴力枚举所有情况，看一个字符匹配一次所有情况。
如果遇到一些识别不了的关键字，看看set里面有没有，没有的话给它加上就能成了。
还是词法分析器比较恶心
词法分析器
实验内容
设计一个应用软件，以实现将正则表达式-->NFA--->DFA-->DFA最小化-->词法分析程序
（1）正则表达式应该支持单个字符，运算符号有： 连接、选择（|）、闭包（*）、括号（）、可选（? ）
（2）读入一行（一个）或多行（多个）正则表达式（可保存、打开正则表达式文件）
（3）需要提供窗口以便用户可以查看转换得到的NFA（用状态转换表呈现即可）
（4）需要提供窗口以便用户可以查看转换得到的DFA（用状态转换表呈现即可）
（5）需要提供窗口以便用户可以查看转换得到的最小化DFA（用状态转换表呈现即可）
（6）需要提供窗口以便用户可以查看转换得到的词法分析程序（该分析程序需要用C/C++语言描述）
（7）扩充正则表达式的运算符号，如 [ ] 、 正闭包（+） 等。
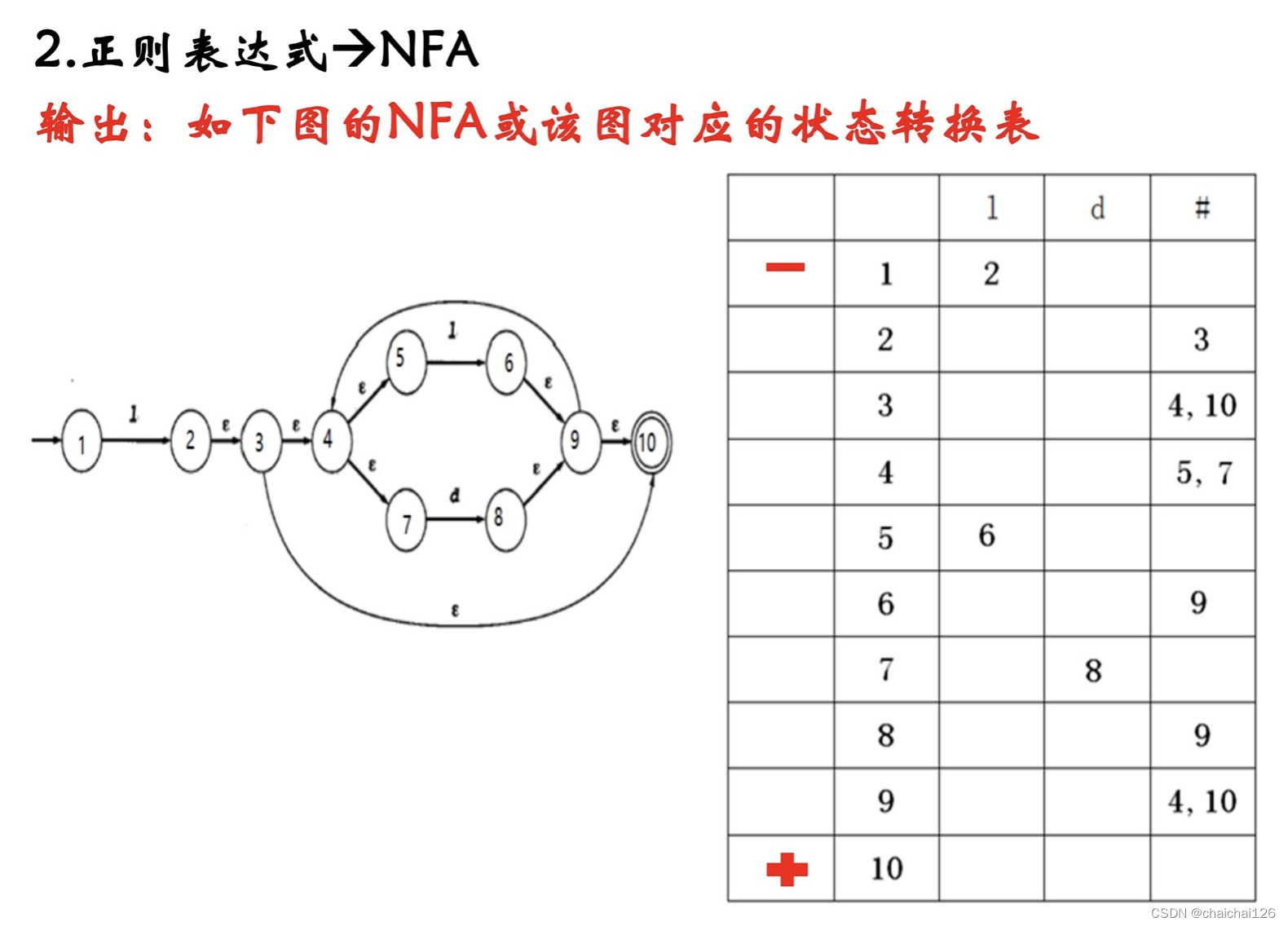
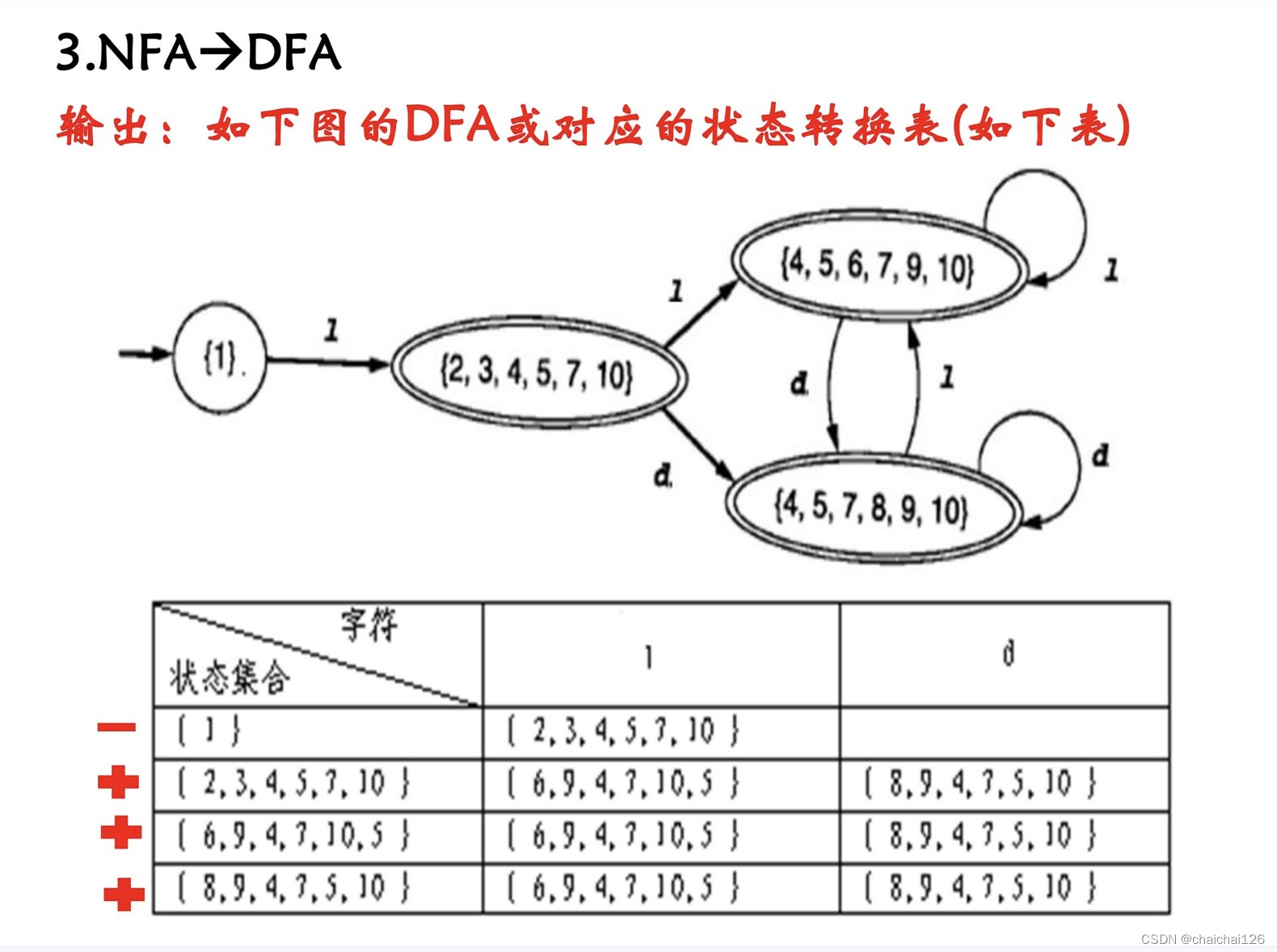
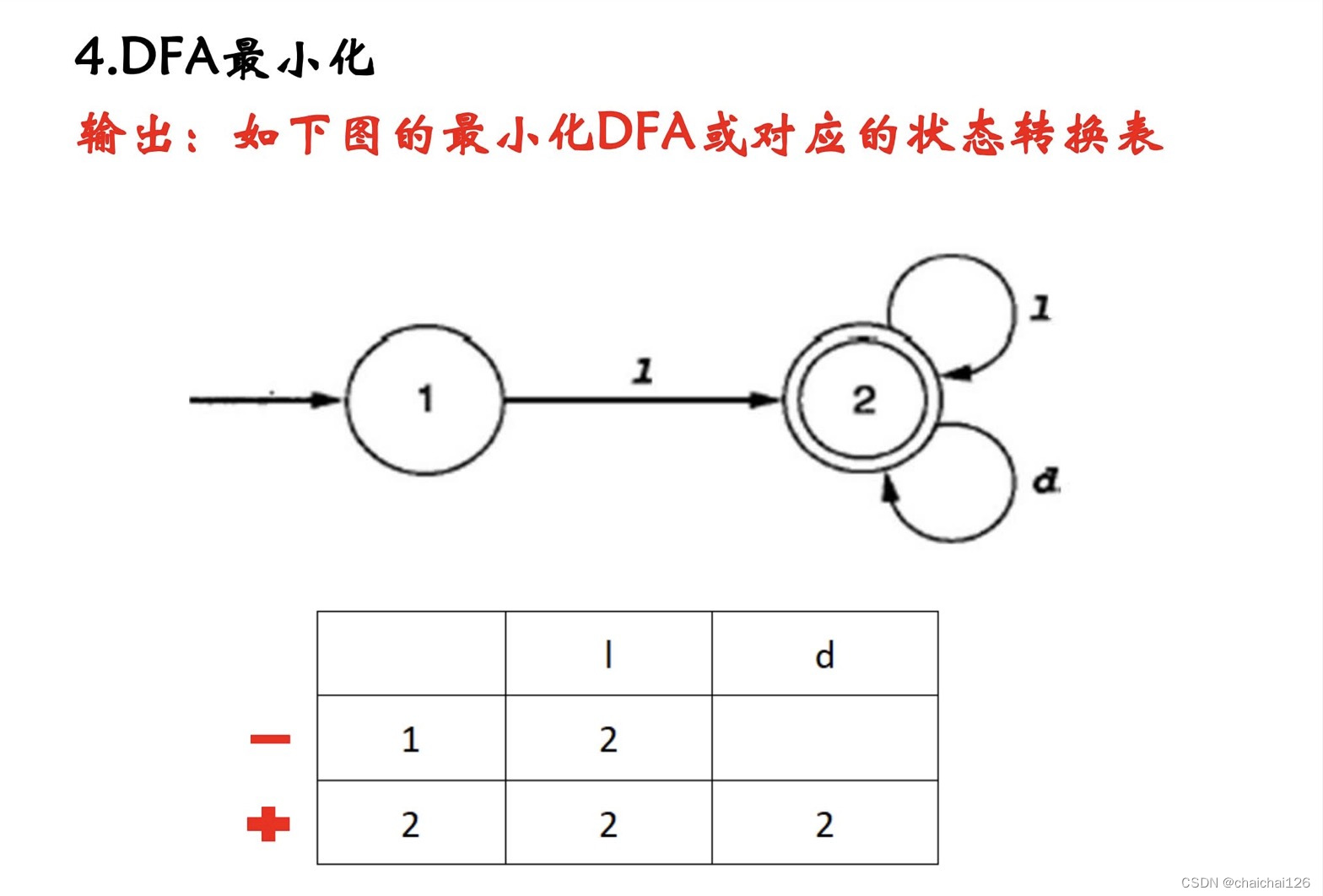
实验思路
程序首先可以识别正则表达式，然后将正则表达式变为NFA，将NFA去空+合成等价得到DFA，再合成等价的到最小化DFA，最后由DFA生成词法分析程序。
个人理解本实验是浴帘想让我们做一个输入自己制定的词法规则（输入正则表达式），然后输出这个词法规则对应的词法分析器。
本次实验使用Thompson's构造法来生成NFA，然后使用了子集构造法来从NFA生成DFA。
部分理论知识
以下是在做实验产生的一些疑惑的解答。
1、为什么NFA引入了空串和分支？它们分别有什么作用？
我们知道，出现NFA是因为直接写出DFA有些困难或麻烦，比如：
考虑串：=、< =和=给出的记号。其中每一个都是一个固定串，但下图不是一个正确的DFA，因为DFA每一个状态的下一个状态都是确定的，不能存在分支。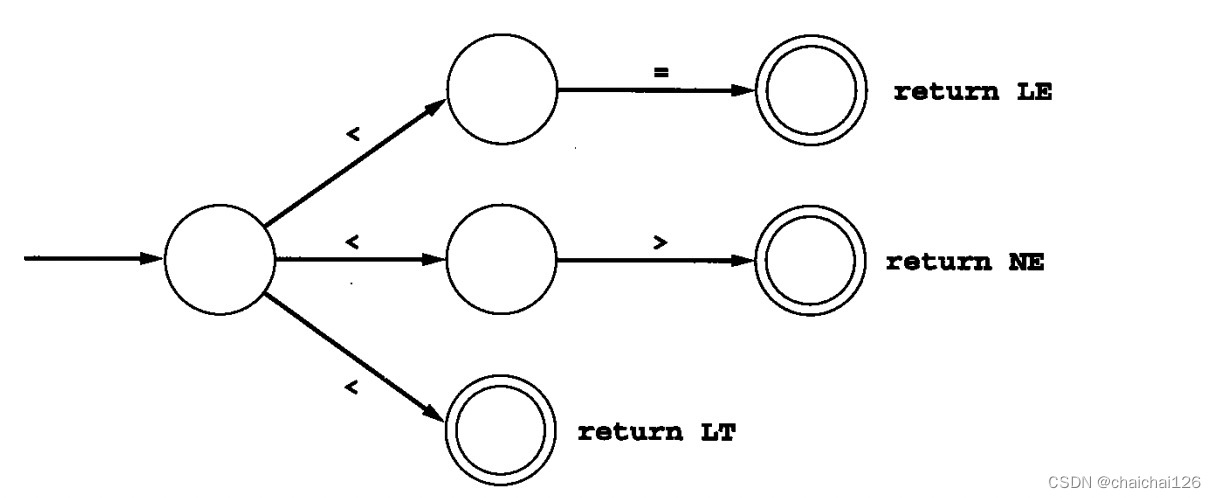
所以最终会把刚才的图合成为下图，这样才是一个DFA(给出一个状态和字符，则通常肯定会有一个指向单个的新状态的唯一转换)：
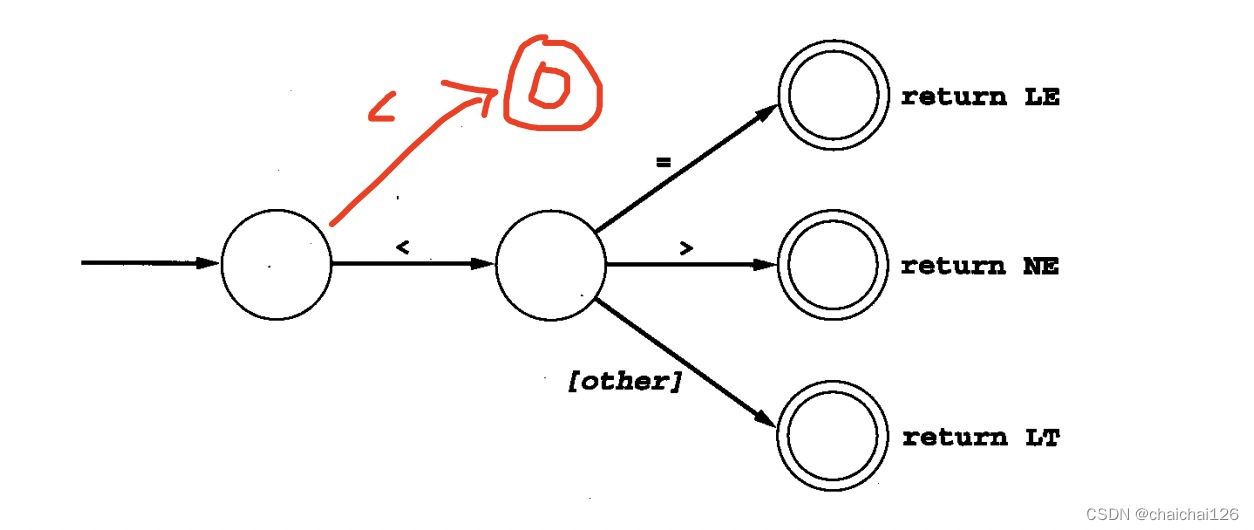比如上图的情况，两个分支都是‘<’，程序会不知道此时应进入哪一个分支，难道我们还得把'<'合成吗？NFA的存在本就是为了解决DFA需要合成的问题，如果NFA也需要合成的话，那它的存在就没什么意义了。 所以此刻就引入了ε-转换，使我们 可以不用合并状态就表述另一个选择。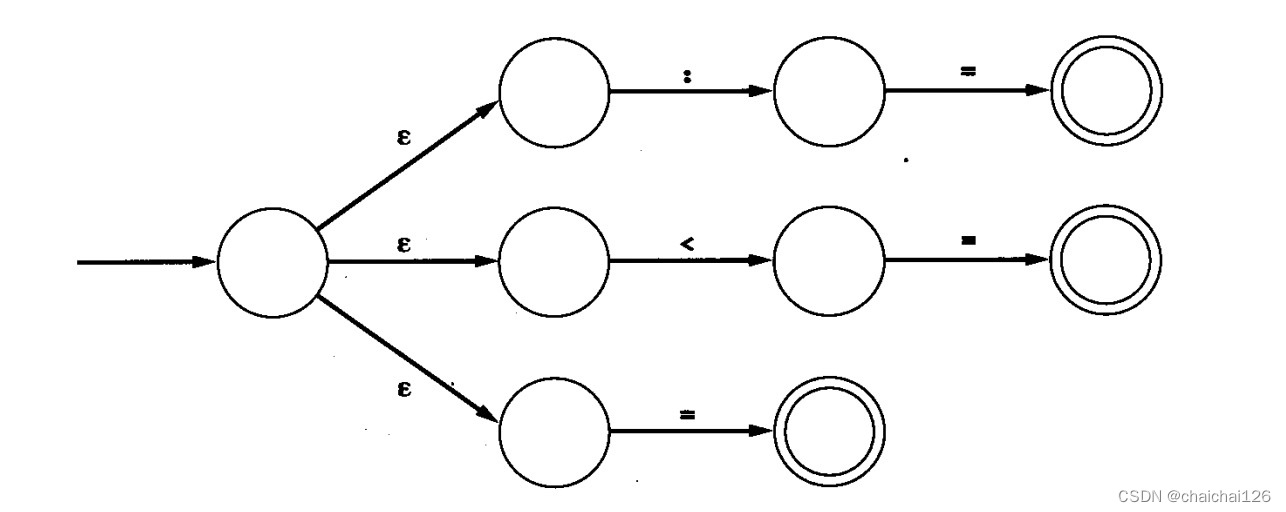 
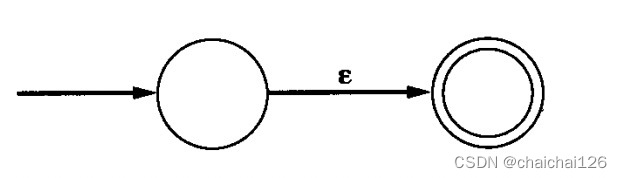DFA表示空串匹配： 
清晰地表示空串匹配同样很有用，有时会使NFA比DFA更直观且更容易表示。
比如说表示正则表达式中的可选部分（即出现0次或1次的部分）。例如，对于正则表达式a?b（表示b前面可以有0个或1个a），又比如说表示正则表达式中的重复部分（即出现0次或多次的部分）。例如，对于正则表达式（a｜b)*。可以自己动手画图尝试一下。
2、最小化DFA，应如何分割不同的非终结集，终结集？
首先回到原因，也就是我们为什么要把DFA最小化？
说白了就是需要效率，所以要把DFA冗余的地方剔除，使程序跑得更快。
明白了原因，我们就知道该怎么做了：最小化DFA就是要剔除DFA冗余的部分；1、合并等价状态（如果两个状态对于所有可能的输入，都转移到相同（或等价）的状态，那么这两个状态就被称为等价状态）2、删除无效状态（无法达到的状态，或者从这些状态无法到达任何终止状态）。
问题又来了，我们应该如何判断等价状态/无效状态？
等价状态的判断：
首先，将所有的状态分为两个集合，一个是终止状态，另一个是非终止状态。然后，反复细化这些集合，对于每个集合和每个输入符号，如果集合中的状态在该输入符号下转移到的状态不在同一个集合中，那么就将这个集合分为两个子集。反复进行这个过程，直到所有的集合都不能再被分割。最后，每个集合中的状态就是等价状态，可以被合并。
举个例子：
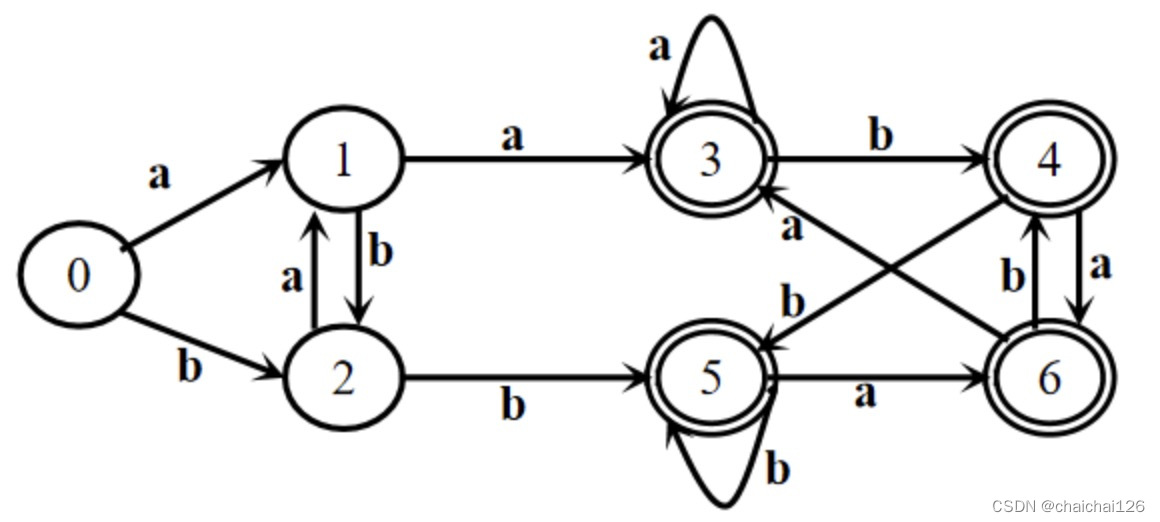
具体该如何判断是否分割：比如说我有两个等价集合：{2, 4} {1, 3}，现在我开始分割{2, 4}等价集合，2输入a走到1，4输入a走到3，此时因为1，3都在一个等价集合中，我们可以看作2,4输入a后都走到了同一个状态，所以我不分割{2, 4}集合。
但如果2输入a走到4，4输入a走到3，他们的终点4，3不属于同一个等价集合，也就是它们不等价，此时我分割{2,4}集合为{2}, {4}。
1、首先开始假设非终结态和终结态分别都等价，构造等价集合：
非终结：{0, 1, 2} 终结：{3, 4, 5, 6}
2、开始观察非终结集合是否等价
输入a:
0 -> 1(属于集合{0, 1 ,2})
1 ->3(属于集合{3, 4, 5, 6})
2 -> 1(属于集合{0, 1, 2})
所以此时0，2等价，3不等价于0，1，分割
此时非终结：{0, 2} {1} 终结：{3, 4, 5, 6}
输入b:
0 -> 2(属于集合{0, 1 ,2})
1 ->2(属于集合{0, 1, 2})
2 -> 5(属于集合{3，4，5，6})
所以此时2不等价于0，再分割
此时非终结：{0} {1} {2} 终结：{3, 4, 5, 6}
3、开始观察终结集合是否等价
输入a:
3 -> 3(属于集合{3, 4, 5, 6})
4 ->6(属于集合{3, 4, 5, 6})
5 -> 6(属于集合{3, 4, 5, 6})
6 -> 3(属于集合{3, 4, 5, 6})
所以此时3,4,5,6等价，不分割
此时非终结：{0} {1} {2} 终结：{3, 4, 5, 6}
输入b
......(不赘述了)
最终得到的最小化DFA结果：非终结：{0} {1} {2} 终结：{3, 4, 5, 6}
A= {0}（初态）、B = {1}、C = {2}、D = {3，4，5，6} （终态）
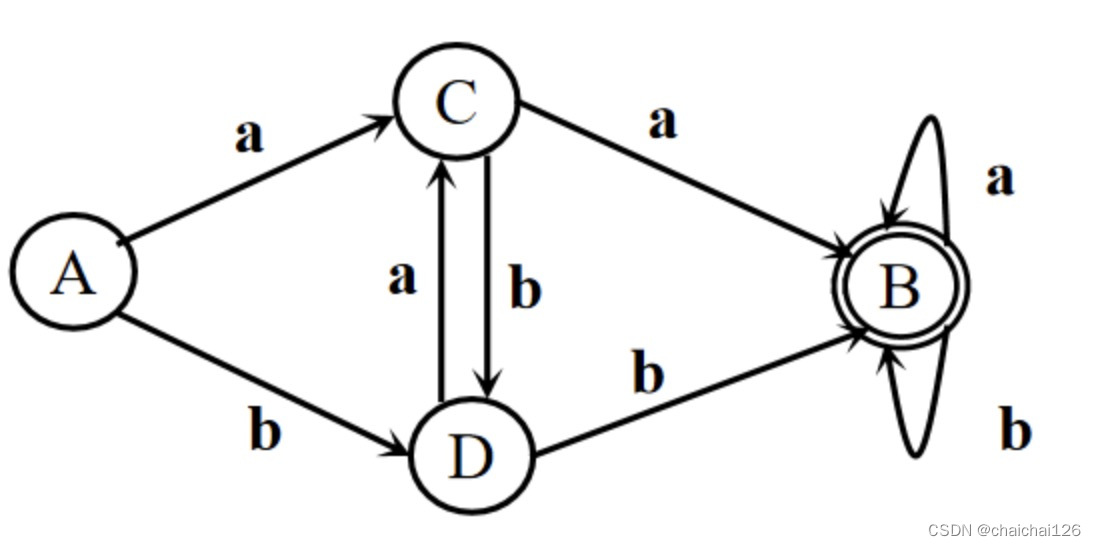
无效状态的判断：
首先，从初始状态开始，标记所有可以到达的状态。然后，从所有的终止状态开始，标记所有可以到达的状态。最后，那些没有被标记的状态就是无效状态，可以被删除。（广搜或深搜）
3、词法分析器的工作
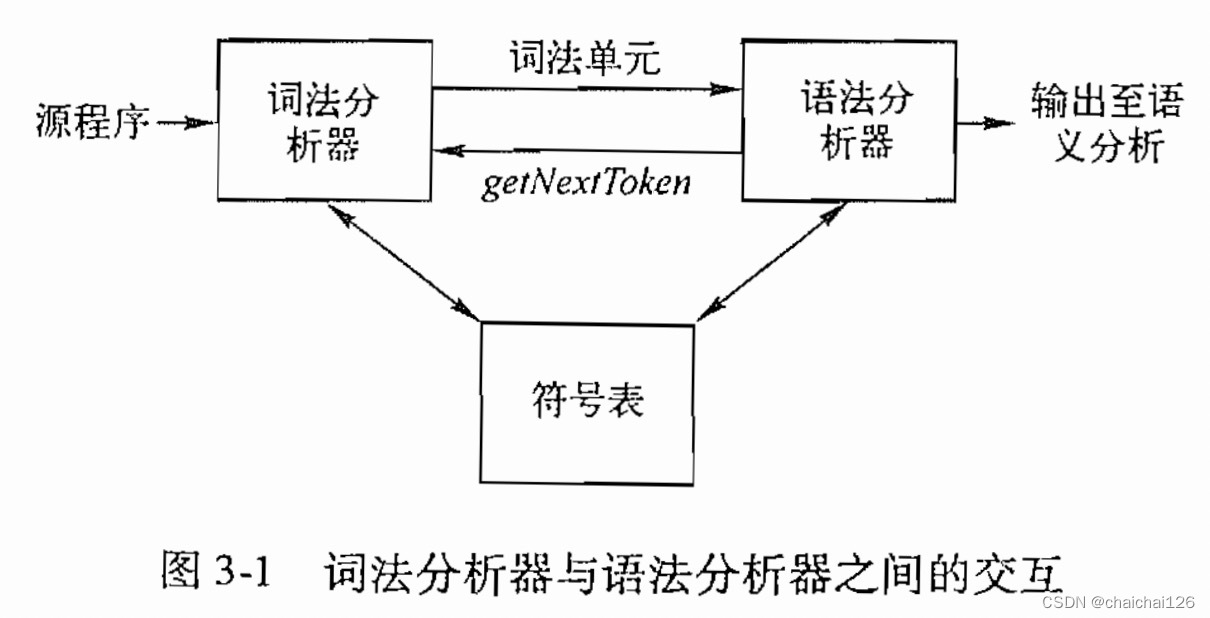
说白了，词法分析器作用如下：
1、读源程序，识别源程序里的符号分别是什么。比如‘+’是运算符加，abc123是一个标识符，识别完成后，把它的识别结果放到符号表里。
2、光把识别结果放到符号表里可不行，语法分析器仍然不知道源程序是什么意思，所以词法分析器还需要把源程序一个词一个词地切开，并按顺序发给语法分析器，语法分析器按顺序接受，并查看符号表这个词到底是什么意思，然后查看目前读到的东西是否符合语法。
3、过滤掉源程序的注释和空白。
重点代码和分析
1、读文件，逐行处理
（本实验可能出现多行正则表达式，浴帘让我们把不同行的表达式用‘｜’相连），所以把实验一的代码抄下来，做一些改动。
（1）将不同行用‘｜’连接，且‘｜’不放在最后一行的末尾，使最终的fileContent只有一行。
（2）如果遇到两个相连的字符，如ab，在中间添加‘&’，表示‘连接’。
#include <stdio.h>#include <string>#include <vector>#include <sstream>#include <iostream>#include <fstream>#include "scanner.hpp"#include "Lex.hpp"using namespace std;vector<string> split(const string &s, char delimiter) { vector<string> tokens; string token; istringstream tokenStream(s); while (getline(tokenStream, token, delimiter)) { tokens.push_back(token); } return tokens;}int main(int argc, const char * argv[]) { // 打开文件 ifstream file("/Users/chaixichi/Desktop/学习资料/大三上/C++lab1/C++lab2/test2.cpp"); //将文件名替换为打开的文件路径 // 查看是否可以打开文件 if (!file) { cout << "Unable to open file"; exit(1); } //将文件中读到的字符串不同行间加‘｜’合成为一行 string temp((istreambuf_iterator<char>(file)), istreambuf_iterator<char>());// //测试split// vector<string>test = split(fileContent, '\n');// for(int i = 0; i < test.size() ;i++){// cout<<test[i]<<endl;// } vector<string> split_temp = split(temp, '\n'); string fileContent_temp, fileContent; for(auto &t : split_temp){ if(t != split_temp.back()){ fileContent_temp += t + '|'; } else{ fileContent_temp += t; } } //将相连两个字符中间加上'&' for(int i = 0; i < fileContent_temp.size(); i++){ if(i + 1 < temp.size() && std::isalpha(fileContent_temp[i]) && std::isalpha(fileContent_temp[i + 1])){ fileContent += fileContent_temp[i]; fileContent += '&'; } else{ fileContent += fileContent_temp[i]; } } //测试fileContent,最终处理结果存在fileContent里 cout<<fileContent; return 0;}现在我们在fileContent里保存了我们处理后的正则表达式。
2、识别正则表达式&生成NFA
即使知道Thompson算法，实现由正则表达式转换到NFA也有些无从下手。
但仔细想想，识别正则表达式，就是要把它的标识符和运算符拆开，并确定运算顺序。
那我们应该如何确定运算顺序？
所用数据结构如下：
cclass MyGraph{public: int mVexNum;//顶点数目 int mEdgeNum;//边的数目 //顶点（所有状态）集合 vector<char> mMatrix[100][100];//邻接矩阵，对应的值为转移条件，就是字母，默认都是空''，表示未连接public: MyGraph();//默认构造函数 void printMyGraph(); //打印输出图内容 void addEdge(int a, int b, char edgeCondition); //增加一条边，边上的值为转换的条件 vector<char> getEdgeValue(int a ,int b);};class NFA{//只有一个结束状态public: vector<int> mVexs;//NFA节点集合，存储的是节点的序号,位置的信息并没有存储内容 MyGraph NFAGraph;//NFA图的结构 int startStatus;//开始状态的序号 int endStatus;//终止状态的序号};//给NFA栈中的元素的定义的一个结构，存储的是起点和终点的信息。struct node{public: int nArray[2];//nArray[0]为起点，nArray[1]为终点 node(int a[2]){//构造函数 for(int i =0;i<2;i++) nArray[i] = a[i]; }};class Lex{public: NFA lexNFA;//NFA结构 DFA lexDFA;//DFA结构 stack <char> operatorStack;//操作符栈 stack <node> NFAStatusPointStack;//NFA栈中的NFA的起始点序号，0的位置代表起点，1的位置代表终点 vector<char> alphabet;//字母表，存储是正则表达式中的字母 ......}重点1:Thompson算法，即用代码实现Thompson算法（下面这几张图）
（1）创造最基本NFA
创造这个最基本的NFA，我们需要：创建两个新节点，创建一条新边，确定这条边的起点和终点
创建新节点时，我们需要：记录新节点 + 设置起点终点
创建新边时，我们需要：增加一条对边的连接，边的条件为我们输入的字符
void Lex::createBasicNFA(char ch){ //据字母创建最基本NFA的操作 int startPoint = lexNFA.mVexs.size() + 1; //分配的节点序号是以前节点序号+1 int endPoint = startPoint + 1; lexNFA.NFAGraph.addEdge(startPoint,endPoint,ch); //增加一个边对边的连接，边的条件是转换条件，就是该字符。 lexNFA.NFAGraph.mVexNum = lexNFA.NFAGraph.mVexNum+2; //增加两个节点 lexNFA.NFAGraph.mEdgeNum++; //边数加1 //添加到节点数组中 lexNFA.mVexs.push_back(startPoint); lexNFA.mVexs.push_back(endPoint); int newNFAStatusPoint[2]; newNFAStatusPoint[0] = startPoint; newNFAStatusPoint[1] = endPoint; NFAStatusPointStack.push(node(newNFAStatusPoint)); //起点终点设置 lexNFA.startStatus = startPoint; lexNFA.endStatus = endPoint;}（2）或‘｜’的运算：
创造这个NFA，我们需要：创建两个新节点，创建4条新边（空输入），确定这四条新边的起点和终点
类比（1），我们可以得出以下代码：
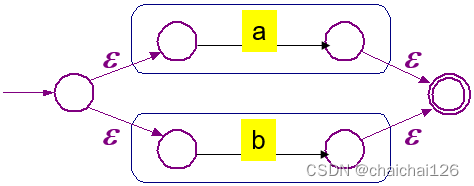
void Lex::selectorCharacterOperation(){ //获取栈顶两个元素，注意，第一个获取的元素为右式，因为栈后进先出 int rightNFA[2]; for(int i = 0; i < 2;i++){ rightNFA[i] = NFAStatusPointStack.top().nArray[i]; } NFAStatusPointStack.pop(); int leftNFA[2]; for(int i = 0; i < 2;i++){ leftNFA[i] = NFAStatusPointStack.top().nArray[i]; } NFAStatusPointStack.pop(); //创建两个新节点 int newStartPoint1 = lexNFA.mVexs.size() + 1; int newStartPoint2 = newStartPoint1 + 1; //比着图连接 lexNFA.NFAGraph.addEdge(newStartPoint1, leftNFA[0], 'E');//空转移 lexNFA.NFAGraph.addEdge(newStartPoint1, rightNFA[0], 'E');//空转移 lexNFA.NFAGraph.addEdge(leftNFA[1], newStartPoint2, 'E');//空转移 lexNFA.NFAGraph.addEdge(rightNFA[1], newStartPoint2, 'E');//空转移 lexNFA.NFAGraph.mVexNum = lexNFA.NFAGraph.mVexNum+2; //节点数目加2 lexNFA.NFAGraph.mEdgeNum = lexNFA.NFAGraph.mEdgeNum + 4; //边的数目加4 //节点添加到节点数组中 lexNFA.mVexs.push_back(newStartPoint1); lexNFA.mVexs.push_back(newStartPoint2); //将新的NFA压入NFA栈中 int newNFAStatusPoint[2]; newNFAStatusPoint[0] = newStartPoint1; newNFAStatusPoint[1] = newStartPoint2; NFAStatusPointStack.push(newNFAStatusPoint); //设置起点终点 lexNFA.startStatus = newStartPoint1; lexNFA.endStatus = newStartPoint2;}3、‘&’与的运算
只多了一条空转移的边
个人觉得是容易设坑的题，因为它看起来很简单，只连一条边即可，但其实不是这么做的。
4、‘*’闭包的运算
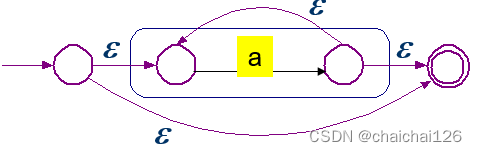
void Lex::repeatCharacterOperation(){ //获取栈顶第一个元素 int top1NFA[2];//开始和结束 for(int i = 0; i < 2;i++){ top1NFA[i] = NFAStatusPointStack.top().nArray[i]; } NFAStatusPointStack.pop(); //创建两个新的节点 int newStartPoint1 = lexNFA.mVexs.size() + 1; int newStartPoint2 = newStartPoint1 + 1; lexNFA.NFAGraph.addEdge(newStartPoint1, newStartPoint2, 'E');//空转移 lexNFA.NFAGraph.addEdge(newStartPoint1, top1NFA[0], 'E');//空转移 lexNFA.NFAGraph.addEdge(top1NFA[1], newStartPoint2, 'E');//空转移 lexNFA.NFAGraph.addEdge(top1NFA[0], top1NFA[1], 'E');//空转移 lexNFA.NFAGraph.mVexNum = lexNFA.NFAGraph.mVexNum + 2;//节点数+2 lexNFA.NFAGraph.mEdgeNum = lexNFA.NFAGraph.mEdgeNum + 4;//节点数+4 //添加到节点数组中 lexNFA.mVexs.push_back(newStartPoint1); lexNFA.mVexs.push_back(newStartPoint2); //将新的NFA压入NFA栈中 int newNFAStatusPoint[2]; newNFAStatusPoint[0] = newStartPoint1; newNFAStatusPoint[1] = newStartPoint2; NFAStatusPointStack.push(node(newNFAStatusPoint)); //起点终点设置 lexNFA.startStatus = newStartPoint1; lexNFA.endStatus = newStartPoint2;}5、‘+’正闭包的运算
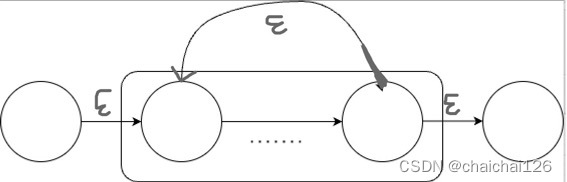
正闭包比起闭包，少了一个空运算
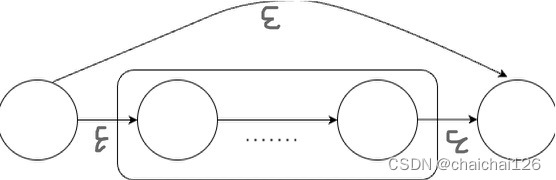
void Lex::repeat1CharacterOperation(){ //弹出一个元素 int topNFA[2]; for(int i = 0; i < 2;i++){ topNFA[i] = NFAStatusPointStack.top().nArray[i]; } //创建两个新节点 int newStartPoint1 = lexNFA.mVexs.size() + 1; int newStartPoint2 = newStartPoint1 + 1; //比着图连接 lexNFA.NFAGraph.addEdge(newStartPoint1, topNFA[0], 'E');//空转移 lexNFA.NFAGraph.addEdge(topNFA[1], newStartPoint2, 'E');//空转移 lexNFA.NFAGraph.addEdge(topNFA[1], topNFA[0], 'E');//空转移 //新节点入节点数组 lexNFA.mVexs.push_back(newStartPoint1); lexNFA.mVexs.push_back(newStartPoint2); //新NFA入栈 int newNFAStatusPoint[2]; newNFAStatusPoint[0] = topNFA[0]; newNFAStatusPoint[1] = topNFA[1]; NFAStatusPointStack.push(node(newNFAStatusPoint)); //记录起点和终点，在全局范围内跟踪NFA的起点和终点 lexNFA.startStatus = newStartPoint1; lexNFA.endStatus = newStartPoint2;}6、‘？’一次或不做的运算
void Lex::once_or_no_CharacterOperation(){ //弹出一个元素 int topNFA[2]; for(int i = 0; i < 2;i++){ topNFA[i] = NFAStatusPointStack.top().nArray[i]; } //创建两个新节点 int newStartPoint1 = lexNFA.mVexs.size() + 1; int newStartPoint2 = newStartPoint1 + 1; //比着图连接 lexNFA.NFAGraph.addEdge(newStartPoint1, topNFA[0], 'E');//空转移 lexNFA.NFAGraph.addEdge(topNFA[1], newStartPoint2, 'E');//空转移 lexNFA.NFAGraph.addEdge(newStartPoint1, newStartPoint2, 'E');//空转移 //新节点入节点数组 lexNFA.mVexs.push_back(newStartPoint1); lexNFA.mVexs.push_back(newStartPoint2); //新NFA入栈 int newNFAStatusPoint[2]; newNFAStatusPoint[0] = topNFA[0]; newNFAStatusPoint[1] = topNFA[1]; NFAStatusPointStack.push(node(newNFAStatusPoint)); //记录起点和终点，在全局范围内跟踪NFA的起点和终点 lexNFA.startStatus = newStartPoint1; lexNFA.endStatus = newStartPoint2;}顺序总结：
（1）根据运算符弹出NFA
（2）创建新节点，创建新边
（3）将新节点入节点数组
（4）将新NFA入栈（起点&终点）
（5）追踪总NFA的起点和终点
重点2:由正则表达式生成NFA状态转移表
（1）生成NFA图
本实验中使用到的正则表达式运算符优先级如下：
| 最优先 | （） |
| 次优先 | *、+、？ |
| 次次优先 | 连接（&） |
| 最后 | ｜ |
该算法能够直接扫描正则表达式并正确地计算运算顺序，主要是因为它使用了一个运算符栈来保存遇到的运算符，并且在遇到新的运算符时，会根据运算符的优先级来决定如何处理运算符栈。
具体来说，当遇到一个新的运算符时，会比较这个运算符和运算符栈顶的运算符的优先级：
（1）如果新的运算符的优先级高于栈顶运算符的优先级，或者运算符栈为空，或者栈顶运算符是'('，则将新的运算符压入运算符栈。
（2） 如果新的运算符的优先级等于或低于栈顶运算符的优先级，则会从运算符栈中弹出运算符，并执行相应的操作，直到栈顶运算符的优先级低于新的运算符的优先级，或者运算符栈为空，或者栈顶运算符是'('。然后，将新的运算符压入运算符栈。
这样，就可以保证在没有括号改变优先级的情况下，高优先级的运算符总是先于低优先级的运算符执行，从而得到正确的运算顺序。
（3）此外，这个算法还使用了一个NFA栈来保存构建过程中的中间结果。每当从运算符栈中弹出一个运算符并执行相应的操作时，都会从NFA栈中弹出相应数量的NFA，并将操作的结果压入NFA栈。这样，就可以保证在处理复杂的正则表达式时，总是先处理子表达式，然后再处理父表达式。
若当前不是一个运算符，创造一个最基本的NFA。
所以，虽然这个算法在扫描正则表达式时并没有显式地标记运算顺序，但是通过使用运算符栈和NFA栈，它能够隐式地确定并遵循正确的运算顺序。
该算法在计算过程中，顺便处理了连接符‘&’添加的问题，比如在正则表达式（a|b)*a中，应该将其变为(a|b)*&a,显式地表示连接，ab变为a&b，显式地表示连接。
void Lex::getNFA(string regexInput){ unsigned long strlen = regexInput.length(); char ch; //扫描正则表达式，建立运算符栈和NFA栈 for(unsigned long i = 0; i < strlen; i++){ ch = regexInput[i]; if(isOperator(ch)){//是运算符 switch(ch){ case '*':{ repeatCharacterOperation(); //如果下一个字符是字母或左括号，需要添加连接符 if((i + 1 < strlen)&&(regexInput[i+1] == '(' || !isOperator(regexInput[i+1]))){ operatorStack.push('&'); } }break; case '+':{ repeat1CharacterOperation(); //如果下一个字符是字母或左括号，需要添加连接符 if((i + 1 < strlen)&&(regexInput[i+1] == '(' || !isOperator(regexInput[i+1]))){ operatorStack.push('&'); } }break; case '?':{ once_or_no_CharacterOperation(); //如果下一个字符是字母或左括号，需要添加连接符 if((i + 1 < strlen)&&(regexInput[i+1] == '(' || !isOperator(regexInput[i+1]))){ operatorStack.push('&'); } }break; case '|':{ if(operatorStack.empty()){ cout<<"运算符栈为空！"<<endl; } else{ ch = operatorStack.top(); while(ch != '('){//这里需要注意 if(ch == '&'){ joinerCharacterOperation(); } else{ break; } operatorStack.pop(); ch = operatorStack.top(); } } operatorStack.push('|');//入栈 }break; case '(':{ operatorStack.push(ch); } case ')':{ ch = operatorStack.top(); while(ch != '('){ switch(ch){ case '&': joinerCharacterOperation(); break; case '|': selectorCharacterOperation(); break; default: break; } operatorStack.pop(); ch = operatorStack.top(); }//end while operatorStack.pop();//移除栈内左括号 //如果下一个字符是字母或者是左括号，需要添加连接符 if((i+1 < strlen)&&(regexInput[i+1] == '(' || !isOperator(regexInput[i+1]))){ operatorStack.push('&'); } }break; default: cout<<"ok"<<ch<<endl; break; }//end switch }//end if else{//不是运算符 auto flag = true;//是否添加到字母表中 for(int i = 0; i < alphabet.size(); i++){ if (ch == alphabet[i]) flag = false; } if(flag){ alphabet.push_back(ch); } //建立一个基本的NFA createBasicNFA(ch); //如果下一个字符是字母的话，就向符号栈中加入一个连接符& if(i+1 <strlen && (!isOperator(regexInput[i+1]) || regexInput[i+1] == '(')){ operatorStack.push('&'); } }//end else }//end for //对最终的NFA栈和运算符栈进行处理（如果不为空） while(!operatorStack.empty()){ ch = operatorStack.top(); switch (ch) { case '|': selectorCharacterOperation(); break; case '&': joinerCharacterOperation(); break; default: break; } operatorStack.pop(); }}总结：每一步都保证高优先级的先运算，要么不入栈直接运算，要么把它留在栈顶。正则表达式遍历结束后继续运算栈中剩下的元素。
最终我们得到了正则表达式字符表，NFA图（NFA邻接表）。
（2）生成NFA状态转移表
在正式开始生成状态转移表之前，我们需要了解两个问题：
1、当获取一个状态转移时，我们需要知道什么？
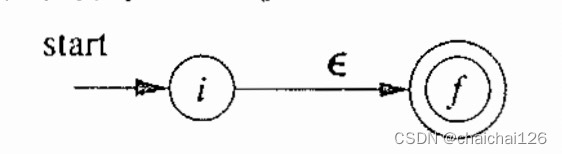
我们需要知道三条信息：
【从哪个状态出发、输入是什么、到达哪个状态】
2、最终生成的状态转移表长什么样？
| 状态/输入字符 | a | b |
| 1 | 1状态输入字符a所到达的状态 | 1状态输入字符b所到达的状态 |
| 2 | 2状态输入字符a所到达的状态 | 2状态输入字符b所到达的状态 |
为了生成状态转移表，我们需要获得：
输入字符集（在刚才生成NFA图时，我们获得的字母表就是输入字符集）
状态集
了解了这些问题，我们就可以生成NFA状态转移表了
邻接矩阵生成相关函数：
class NFA{ ...... MyGraph NFAGraph;//存储NFA的图结构 ......}//默认构造函数,初始边和顶点数目都为0MyGraph::MyGraph():mVexNum(0),mEdgeNum(0){ for(int i =0;i<100;i++){ for(int j =0;j<100;j++){ mMatrix[i][j].push_back('^') ; } }}//增加一条边 a：节点名称、b：另一个节点名称、edgeCondition ：边上的值，即转换条件void MyGraph::addEdge(int a, int b, char edgeCondition){ if (mMatrix[a][b].at(0) == '^'){ mMatrix[a][b].clear(); } bool flag = true; for (int i = 0; i < mMatrix[a][b].size() ; ++i) { if (mMatrix[a][b].at(i) == edgeCondition){ flag = false; break; } } if (flag){//若没有这样的边 mMatrix[a][b].push_back(edgeCondition);//加入 }}最终得到的邻接矩阵mMatrix长这样：
| 到达\出发 | 1 | 2 | 3 |
| 1 | a | a | |
| 2 | b | E(空状态) | |
| 3 | b |
横着的表头表示从哪个状态出发，竖着的表头表示到达哪个状态，中间表示从xx状态出发，到xx状态，需要输入xx
与状态转移表StatusMatrix作对比：
| 状态/输入字符 | a | b | E(空字符) |
| 1 | 1状态输入字符a所到达的状态 | 1状态输入字符b所到达的状态 | 1状态输入空字符所到达的状态 |
| 2 | 2状态输入字符a所到达的状态 | 2状态输入字符b所到达的状态 | 2状态输入空字符所到达的状态 |
| 3 | ..... | .... | ...... |
我们发现，逐列遍历mMatrix即可把它转化成状态转移表
比如说，第一列代表从状态1出发，我们看到第一列第一行，即，mMatrix[0][0] == 'a'，把它放到对应状态转移表的位置StatusMatrix[0][0]，StatusMatrix[0][0] == 0，即代表从状态1出发，输入a（在状态转移表中，以a在字母表中的下标代替a)，到达状态1
代码就不赘述了，就是一个遍历的问题。
3、NFA转DFA
采用子集构造法从NFA转DFA，我愿称其为，疯狂地求ε闭包。
我们知道，NFA比DFA多的东西就是空转移&分支，所以将NFA转换为DFA，就是把空转移和分支去掉，能合并的合并。
此处需要引入一个等价集合的概念，即，某个节点在经历ε闭包运算后，所得到的集合，我们称它为等价集合。
用一道具体的题目举例：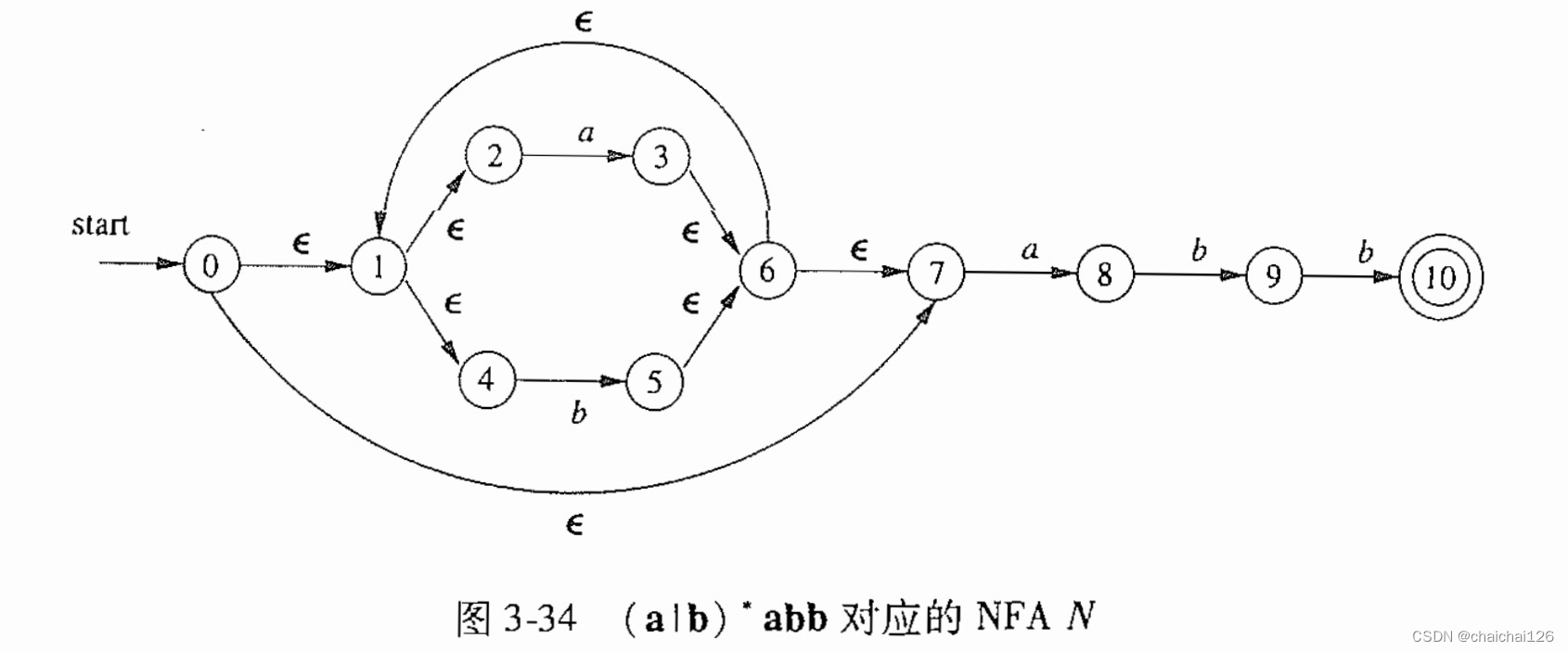
我们可以清楚地看到，这幅NFA图从状态0开始，但是它的初始状态不仅仅是状态0，应该是从状态0，经过一个或多个ε所达到的状态集合
（1）所以上图初始状态集合为：{0, 1, 2, 4, 7}，记为集合A，它是一个等价集合。
该NFA的字母表是{a, b}
（2）我们先向集合A中输入状态a，看它经过一个a（期间可经过多个ε）后，得到的集合
{1, 2, 3, 4, 6, 7，8},记为集合B，它是一个等价集合，表示向等价集合A中输入一个a后，所能到达的终点集合。
（3）我们再向集合A中输入状态b，看它经过一个a（期间可经过多个ε）后，得到的集合
{1, 2, 4, 5, 6, 7},记为集合C，它是一个等价集合。
（4）我们再向集合B中输入状态a，看它经过一个a（期间可经过多个ε）后，得到的集合
{1, 2, 3, 4, 6, 7, 8},与集合B相同，没有产生新的集合。
（5）我们再向集合B中输入状态b，看它经过一个b（期间可经过多个ε）后，得到的集合
{1, 2, 3, 4, 5，6, 7，9},产生新的集合D，它是一个等价集合。
.......不断地尝试，直到再也无法出现新的集合
最终得到：
用图3-35生成的DFA图
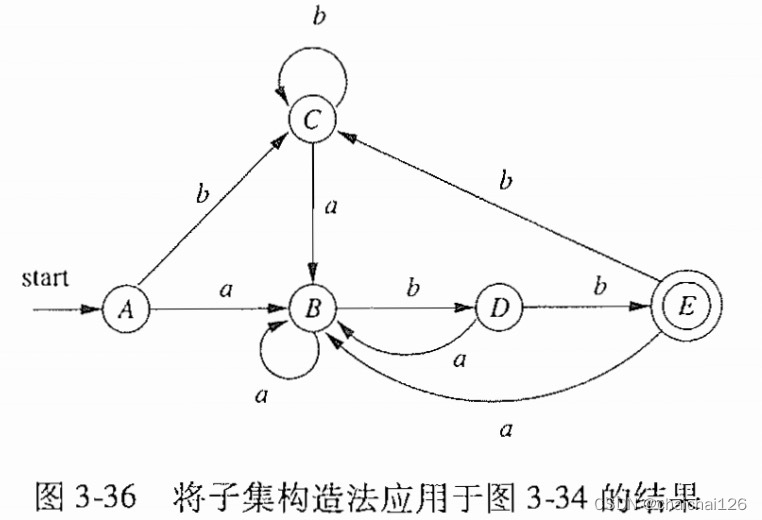
也就是说，我们将问题转化为，按照刚才的ε闭包运算规则，从初始状态集合开始，根据字母表（输入的状态表）不断尝试生成新集合，并对新集合进行ε闭包运算，直到不生成新集合，最后生成图3-35的表即可。
ε闭包运算，以下代码把它拆成两部分来实现。
第一部分是计算能从NFA的状态数组statusArray中的某个状态s开始只通过E转换到达的NFA状态元素。
第二部分是能够从NFA的状态数组statusArray中的某个状态出发，通过条件为condition转换到达的NFA状态集合。
将生成步骤总结如下：
（1）输入状态数组，将状态数组压入resultArray和statusArray。
（2）将statusArray里的元素一个个出栈，直到statusArray里为空，每出栈一个元素（状态），在邻接表里寻找是否有：由出栈状态输入指定字符（‘E’/condition）后达到的状态，如果有，将达到的状态压入statusArray和resultArray。
（3）将resultArray去重，返回，返回的resultArray就是输入的状态集合输入（‘E’/condition）所能到达的状态集合。
//DFA：能从NFA的状态数组statusArray中的某个状态s开始只通过E转换到达的NFA状态元素vector<int> Lex::e_closure(vector<int> statusArray){ vector<int> resultsArray;//存放状态数组的E转换集合 stack<int> statusStack;//存放递归过程中的状态，当该栈为空时，递归结束 for(int i = 0; i < statusArray.size(); i++){ statusStack.push(statusArray[i]);//初始化状态栈 resultsArray.push_back(statusArray[i]);//状态本身也可以通过空转换到本身，所以要将自身添加到结果数组 } while(!statusStack.empty()){ int status = statusStack.top(); statusStack.pop(); for(int i = 1; i < lexNFA.mVexs.size() + 1; i++){ if(i == status){//查看以当前状态为起点的邻接表 for(int j = 1; j < lexNFA.mVexs.size() + 1; j++){ if(lexNFA.NFAGraph.getEdgeValue(i, j).at(0) == 'E'){//若转移条件为‘E’ statusStack.push(j); resultsArray.push_back(j); } } } }//end for }//end while //去除重复元素 sort(resultsArray.begin(), resultsArray.end()); resultsArray.erase(unique(resultsArray.begin(), resultsArray.end())); return resultsArray;}//DFA:能够从NFA的状态数组statusArray中的某个状态出发，通过条件为condition转换到达的NFA状态集合vector<int> Lex::nfaMove(vector<int> statusArray, char condition){ vector<int> resultArray;//结果数组 stack<int> statusStack;//状态栈 //状态集入栈 for(int i = 0 ; i < statusArray.size(); i++){ resultArray.push_back(statusArray[i]); statusStack.push(statusArray[i]); } //开始找 for(int i = 1; i < lexNFA.mVexs.size(); i++){ if(statusArray[i] == i){ for(int j = 1; j < lexNFA.mVexs.size(); i++){ if(lexNFA.NFAGraph.getEdgeValue(i, j).at(0) == condition){ resultArray.push_back(j); statusStack.push(j); } } } }//end for //去重 sort(resultArray.begin(), resultArray.end()); resultArray.erase(unique(resultArray.begin(), resultArray.end())); return resultArray; }那这两个函数应该如何调用，以模拟手动的计算过程？
回想一下我们手动的运算顺序：先利用ε闭包生成初始状态集合，然后向初始状态集合里依次投入字母表中的元素，试图生成一个新的集合，生成新的集合后，我们向这个集合里依次投入字母表中的元素，试图生成一个新的集合，直到最终无法生成新集合为止。
（1）利用ε闭包生成初始状态集合。
void Lex::getDFA(){ //给DFA节点开头位置加一个空元素占位 lexDFA.mVexs.emplace_back(0); vector<int> initStatus; initStatus.push_back(lexNFA.startStatus); vector<int> initStatusTrans(e_closure(vector<int>(initStatus)));//生成初始状态集合 //给DFA创建第一个节点 int newDFAStartPoint = lexDFA.DFAGraph.mVexNum + 1; lexDFA.DFAGraph.mVexNum++;//节点数+1 //DFA起点确定 lexDFA.startStatus = newDFAStartPoint; stack<int> DFAStatusStack;//DFA状态栈 DFAStatusStack.push(newDFAStartPoint); lexDFA.mVexs.push_back(initStatus);//NFA起点的等价集合为DFA的起点 ......... }（2）根据初始状态集合，计算DFA
首先要解决的问题是，我们应该如何判断什么时候停止？即，什么时候不再产生新状态。
答案是利用一个DFAStatusStack，当我们生成一个集合，尝试入栈时，判断该集合是否在我们已经生成的DFA中，若是，则不压入。
直到DFAStatusStack为空，即不再产生新的集合需要运算。
void Lex::getDFA() { //给DFA节点开头位置加一个空元素占位 lexDFA.mVexs.emplace_back(0); vector<int> initStatus; initStatus.push_back(lexNFA.startStatus); vector<int>initStatusTrans(e_closure(vector<int>(initStatus))); //给DFA创建第一个节点 int newDFAStartPoint = lexDFA.DFAGraph.mVexNum + 1; lexDFA.DFAGraph.mVexNum ++;//节点数加1 lexDFA.startStatus = newDFAStartPoint; stack<int> DFAStatusStack;//存储还没有经过字母表转换的DFA状态, DFA状态栈,这个栈只需要存储DFA的序号就可以了，没存储DFA节点对应的NFA集合， DFAStatusStack.push(newDFAStartPoint); lexDFA.mVexs.push_back(initStatusTrans);//NFA起点的E转换集合赋值给DFA的第一个节点 while (!DFAStatusStack.empty()){ int topDFAStack = DFAStatusStack.top(); DFAStatusStack.pop(); for (int i = 0; i < alphabet.size() ; ++i) { //对字母表的每个元素都需要作为转换条件 vector<int> tempArray = e_closure(nfaMove(lexDFA.mVexs[topDFAStack],alphabet[i])); if (tempArray.empty()){//如果转换产生的NFA集合为空，跳过该次转换即可 continue; } int position = isDFAStatusRepeat(tempArray);//判断新生成DFA状态是否已经存在了，如果已经存在，返回该状态在节点的位置 if (position == -1){//这个是新生成的DFA状态，没有重复 int tempDFAStatusNode = lexDFA.DFAGraph.mVexNum + 1; lexDFA.DFAGraph.mVexNum ++;//节点数加1 if (isEndDFAStatus(tempArray)){ lexDFA.endStatus.push_back(tempDFAStatusNode); } lexDFA.mVexs.push_back(tempArray);//把NFA集合赋值给DFA的状态 DFAStatusStack.push(tempDFAStatusNode);//把新产生的DFA状态加入到DFA栈中 position = tempDFAStatusNode; } //连接节点，产生边 lexDFA.DFAGraph.addEdge(topDFAStack,position,alphabet[i]); lexDFA.DFAGraph.mEdgeNum ++; } }}//判断是否是DFA的终止状态，只要包含了NFA的终止状态的DFA状态都是终止状态bool Lex::isEndDFAStatus(vector<int> nfaArray){ for (int i = 0; i < nfaArray.size(); ++i) { if (lexNFA.endStatus == nfaArray[i]){ return true; } } return false;}//判断新产生的DFA状态是否已经存在DFA状态表中int Lex::isDFAStatusRepeat(vector<int> a){ int position = -1; for (int i = 1; i < lexDFA.mVexs.size()+1; ++i) { if (a == lexDFA.mVexs[i]){ position = i; break; } } return position;}有同学可能会疑惑，为什么只在生成开始状态集的时候调用了一次空运算（e-closure），其他集合都在用nfaMove生成，那是因为在生成NFA邻接表时，空串不影响最终抵达的状态。
4、最小化DFA
在手动计算中，在得到DFA后，首先划分非终结态和终结态集合，然后尝试字母表中所有输入，试图再次分割非终结态和终结态集合。
例：假设我有一个非终结态集合（是一个等价集合）{1, 2, 3, 4},一个终结态集合（是一个等价集合）{5, 6}
我的字母表是{a, b}
(1)尝试向非终结态集合{1, 2, 3, 4},输入a
1输入a到2 2输入a到2 3输入a到1 4输入a到3
最终得到的终点集合为{2,1,3}，因为它属于我们的等价集合，不划分。
(2)尝试向非终结态集合{1, 2, 3, 4},输入b
1输入a到6 2输入a到2 3输入a到5 4输入a到3
最终得到的终点集合为{2,3,5,6}，其中{2,3}属于{1, 2, 3, 4},{5, 6}属于{5,6}
所以划分非终态集合{1, 2, 3, 4}为{1, 3},{2, 4}
(3)尝试向终结态集合{5， 6},输入a
。。。。。。。以此类推
所以，我们代码模拟的就是，找到非终结集合、终结集合，然后向其中逐个输入字母表，得到终点集，判断终点集是否属于同一个等价集合，如果不是，按照终点集划分，如果是，不划分。
首先，将DFA的状态分为两类：终止状态和非终止状态。这两类状态被分别存储在endPointArray和noEndPointArray中。
将这两个数组被添加到dividedArrays中，这是 一个对 的数组，其中每个对的第一个元素是一个状态数组，第二个元素是一个布尔值，表示该状态数组是否可以进一步划分。
void Lex::minimizeDFA(){ vector<int> noEndPointArray;//非终止状态集合 vector<int> endPointArray(lexDFA.endStatus);//终止状态集合 //初始化非终止状态集合 for(int i = 0; i < lexDFA.mVexs.size(); i++){ if(!isInDFAEndStatus(i)){//不在终止状态集合里 noEndPointArray.push_back(i); } } vector<pair<vector<int>, bool>> dividedArrays;//first存储的是划分的集合，second存储的是该划分集合是否可继续划分 dividedArrays.emplace_back(noEndPointArray, true); dividedArrays.emplace_back(endPointArray, true); ........... }然后，代码进入一个循环，直到所有的状态数组都不能进一步划分为止。在每次循环中，代码会遍历dividedArrays中的每个状态数组。对于每个状态数组，代码会遍历字母表中的每个字母，然后对状态数组中的每个状态，找到通过当前字母转换后的状态，并找到这个状态所在的状态数组的序号。然后，根据这些序号，将当前状态数组进一步划分。
这部分代码有些长，我想还是把它拆开看吧
首先是：在每次循环中，代码会遍历dividedArrays中的每个状态数组。对于每个状态数组，代码会遍历字母表中的每个字母，然后对状态数组中的每个状态，找到通过当前字母转换后的状态，并找到这个状态所在的状态数组的序号。
定义一些要用到的数据结构：
void Lex::minimizeDFA(){ vector<int> noEndPointArray;//非终止状态集合 vector<int> endPointArray(lexDFA.endStatus);//终止状态集合 //初始化非终止状态集合 for(int i = 0; i < lexDFA.mVexs.size(); i++){ if(!isInDFAEndStatus(i)){//不在终止状态集合里 noEndPointArray.push_back(i); } } vector<pair<vector<int>, bool>> dividedArrays;//first存储的是待划分的集合，second存储的是该划分集合是否可继续划分 dividedArrays.emplace_back(noEndPointArray, true); dividedArrays.emplace_back(endPointArray, true); bool flag = true; while(flag){ for(int j = 0; j < dividedArrays.size(); j++){//对划分的每个集合进行操作 int canNotBeDivided = 0;//标记是否当前集合可以被划分,1为不可 if(dividedArrays[j].first.size() == 1){//该集合元素只有一个，必不可划分 dividedArrays[j].second = false; continue; vector<int> arrayNumVector;//存放DFA状态经过某个字母转换到的结果集 vector<pair<int, int>> statusMap;//存放每个节点结果集序号 该节点本身序号 } }//end for j }//end while}然后，正式开始对 待划分 的每个集合进行操作（逐个尝试输入字母表中的符号，记录结果集，查看结果集是否在一个等价集合中）
j循环，尝试对划分的每个集合进行操作
i循环，当前划分的集合尝试逐个输入字符表
k循环，对当前划分的集合尝试输入当前字符，逐个记录当前划分的集合元素序号 到 当前划分的集合输入当前字符后所到达的状态属于的等价集合 的映射
//最小化DFAvoid Lex::minimizeDFA(){ ......... vector<pair<vector<int>, bool>> dividedArrays;//first存储的是待划分的集合，second存储的是该划分集合是否可继续划分 dividedArrays.emplace_back(noEndPointArray, true); dividedArrays.emplace_back(endPointArray, true); bool flag = true; while(flag){ for(int j = 0; j < dividedArrays.size(); j++){//对划分的每个集合进行操作 int canNotBeDivided = 0;//标记是否当前集合可以被划分,1为不可 if(dividedArrays[j].first.size() == 1){//该集合元素只有一个，必不可划分 dividedArrays[j].second = false; continue; } vector<int> arrayNumVector;//存放DFA状态经过某个字母转换到的结果集 vector<pair<int, int>> statusMap;//存放每个节点结果集序号 该节点本身序号 for(int i = 0; i < alphabet.size(); i++){ for(int k = 0; k < dividedArrays[j].first.size(); k++){ //获取待划分集合的每个元素转换状态属于的集合序号 int transStatus = lexDFA.getTargetStatus(dividedArrays[j].first[k], alphabet[i]); //看我们当前得到的转换状态属于哪个待划分集合 int statusInArrayNum = getContainPosition(transStatus, dividedArrays); if(statusInArrayNum == -1){//没有转换结果，也就是当前元素无法接收alpha[i] arrayNumVector.push_back(statusInArrayNum); } else{//当前元素可以接收alpha[i] if(!isContain(statusInArrayNum, arrayNumVector)){//避免结果集中状态重复 arrayNumVector.push_back(statusInArrayNum); } } statusMap.emplace_back(statusInArrayNum, dividedArrays[j].first[k]);//将元素转换状态属于的集合序号 该元素本身序号压入 }//end for k }//end for i }//end for j }//end while}拿到这个映射后，我们就可以根据这个映射划分集合了，将映射到相同等价集合的元素划为一个集合
看起来有些复杂，其实整体的思路如下
（1）设定一个数组，arrayNumVector，用于存放当前DFA状态集经过某个字母转换到的结果集，不断尝试向当前DFA状态集中放入字母，如果集合元素无法接受当前字母，记为-1，入arrayNumVector，如果可以接收，记接收后转换到的状态，入arrayNumVector。
顺便设定一个Map,statusMap，记录当前元素输入当前字母后，它的转换后的状态属于我们划分的哪个集合。（划分集合号，当前状态）
（2）得到当前DFA状态集经过某个字母转换到的结果集arrayNumVector，当前状态与划分的集合的映射statusMap后，开始判断是否要划分。
若结果集只有一个元素，无论如何都不需要划分，如果有多个元素，检查statusMap判断是否要划分。
遍历statusMap，将当前集合号相同 的状态划入一个数组，如果最后得到的数组与已有的划分集合相同，将当前在看的划分集合标记为false，表示不能再划分。
如果最后得到的数组与已有的划分集合不同，压入划分集合，删除划分集合中当前在看的划分集合，表示当前集合已经划分为压入的划分集合。
（3）遍历划分集合数组，若都为false，表示都不能划分，划分结束，退出划分循环，开始合并DFA等价状态。
void Lex::minimizeDFA(){ ...... vector<pair<vector<int>, bool>> dividedArrays;//first存储的是待划分的集合，second存储的是该划分集合是否可继续划分 dividedArrays.emplace_back(noEndPointArray, true); dividedArrays.emplace_back(endPointArray, true); bool flag = true; while(flag){ for(int j = 0; j < dividedArrays.size(); j++){//对划分的每个集合进行操作 int canNotBeDivided = 0;//标记是否当前集合可以被划分,1为不可 if(dividedArrays[j].first.size() == 1){//该集合元素只有一个，必不可划分 dividedArrays[j].second = false; continue; } vector<int> arrayNumVector;//存放DFA状态经过某个字母转换到的结果集 vector<pair<int, int>> statusMap;//存放每个节点结果集序号 该节点本身序号 for(int i = 0; i < alphabet.size(); i++){ for(int k = 0; k < dividedArrays[j].first.size(); k++){ //获取待划分集合的每个元素转换状态属于的集合序号 int transStatus = lexDFA.getTargetStatus(dividedArrays[j].first[k], alphabet[i]); //看我们当前得到的转换状态属于哪个待划分集合 int statusInArrayNum = getContainPosition(transStatus, dividedArrays); if(statusInArrayNum == -1){//没有转换结果，也就是当前元素无法接收alpha[i] arrayNumVector.push_back(statusInArrayNum); } else{//当前元素可以接收alpha[i] if(!isContain(statusInArrayNum, arrayNumVector)){//避免结果集中状态重复 arrayNumVector.push_back(statusInArrayNum); } } statusMap.emplace_back(statusInArrayNum, dividedArrays[j].first[k]);//将元素转换状态属于的集合序号 该元素本身序号压入 }//end for k if(arrayNumVector.size() == 1){//DFA状态经过某个字母转换到的结果集只有1个 canNotBeDivided++; continue;//不划分，看下一个字母 } else{//开始划分 for(int l = 0; l < arrayNumVector.size(); l++){ vector<int> tempArray; for(int k = 0; k < statusMap.size(); i++){ if(arrayNumVector[l] == -1 && statusMap[k].first == -1){ statusMap[k].first = -2;//-2代表删除状态 tempArray.push_back(statusMap[k].second); break; } else{ if(statusMap[k].first == arrayNumVector[l]){//根据集合序号划分 tempArray.push_back(statusMap[k].second); } } dividedArrays.emplace_back(tempArray, true); }//end k auto iter = dividedArrays.begin() + j; dividedArrays.erase(iter); j--; break;//当前集合结束，调到下一个位置的集合，因为删除了该元素，其他元素前移一位,所以j-- }//end l } }//end for i if(canNotBeDivided == alphabet.size()){ dividedArrays[j].second = false; } }//end for j //判断是否结束循环，如果划分集合下面所有集合都不可分就推出循环 flag = false; for(int m = 0; m < dividedArrays.size(); m++){ if(dividedArrays[m].second == true){ flag = true; break; } }//end for m }//end while }合并DFA等价状态：遍历划分集合，把每个划分集合都合成为一个点，合成后给每个点分配编号
void Lex::mergeTwoNode(int a,int b){ for (int i = 1; i < lexDFA.mVexs.size()+1 ; ++i) { if (i == b){ for (int j = 1; j < lexDFA.mVexs.size()+1 ; ++j) { if (lexDFA.DFAGraph.getEdgeValue(b,j).at(0) != '^'){ if (j == b){ lexDFA.DFAGraph.addEdge(a,a,lexDFA.DFAGraph.getEdgeValue(b,j).at(0)); } else{ lexDFA.DFAGraph.addEdge(a,j,lexDFA.DFAGraph.getEdgeValue(b,j).at(0)); } lexDFA.DFAGraph.deleteEdge(b,j); lexDFA.mVexs[b] = vector<int>(); } } } else{ for (int j = 1; j < lexDFA.mVexs.size() + 1; ++j) { if (j == b && lexDFA.DFAGraph.getEdgeValue(i,b).at(0)!='^'){ lexDFA.DFAGraph.addEdge(i,a,lexDFA.DFAGraph.getEdgeValue(i,b).at(0)); lexDFA.DFAGraph.deleteEdge(i,j); lexDFA.mVexs[b] = vector<int>(); break; } } } }}void Lex::minimizeDFA() { vector<int> noEndPointArray;//非终止态节点集合 vector<int> endPointArray(lexDFA.endStatus); //非终止状态集合 for (int i = 1; i < lexDFA.mVexs.size(); ++i) { if (!isInDFAEndStatus(i)){ noEndPointArray.push_back(i); } }//初始化非终止节点集合 cout << endl; //终止状态集合 for (int n = 0; n < endPointArray.size(); ++n) { cout << endPointArray[n] << " "; } cout << endl; vector<pair<vector<int>,bool>> dividedArrays;//first存储的是划分的集合，second存储的是该划分集合是否可继续划分 dividedArrays.emplace_back(noEndPointArray, true); dividedArrays.emplace_back(endPointArray, true); bool flag = true; while(flag){ for (int j = 0; j < dividedArrays.size(); ++j) {//对划分的每个集合进行操作 cout << endl; int canNotBeDivided = 0;//经过一次字母表的转换，如果该集合的转换状态只有一个，说明该集合不能被该字母区分，该变量+1 if (dividedArrays[j].first.size() == 1){ dividedArrays[j].second = false;//如果集合元素只有一个，赋值为false，即不可再划分 continue; } for (int i = 0; i < alphabet.size() ; ++i) { for (int m = 0; m < dividedArrays[j].first.size(); ++m) { cout << dividedArrays[j].first[m] << " "; } cout << "当前字母为" << alphabet[i] << endl; vector<int> arrayNumVector;//存放DFA状态经过某个字母转换到的集合序号的数组 //first 为转换状态属于的集合序号，second DFA起点的状态节点 vector<pair<int,int>> statusMap;//存放了每个节点的转换后属于的集合序号——该节点本身序号 for (int k = 0; k < dividedArrays[j].first.size(); ++k) { //获取到该集合的每个元素的转换状态属于的集合序号 int transStatus = lexDFA.getTargetStatus(dividedArrays[j].first[k],alphabet[i]);//获取节点的转换DFA节点 int statusInArrayNum = getContainPosition(transStatus,dividedArrays);//转换状态属于的集合序号 if(statusInArrayNum == -1){//必须进行划分，这个时候虽然没有转换结果，所以需要将集合序号人为设置一个唯一的数 statusInArrayNum = -1; arrayNumVector.push_back(statusInArrayNum); }else{ if (!isContain(statusInArrayNum,arrayNumVector)){//防止集合序号的重复 arrayNumVector.push_back(statusInArrayNum);//将集合序号加入到集合序号数组中 } } statusMap.emplace_back(statusInArrayNum,dividedArrays[j].first[k]);//将集合序号————对于的DFA状态组压入 } if (arrayNumVector.size() == 1){ canNotBeDivided ++ ; continue; }else{ for (int m = 0; m < arrayNumVector.size(); ++m) { } for (int l = 0; l < arrayNumVector.size(); ++l) {//进行划分 vector<int> tempArray; for (int k = 0; k < statusMap.size(); ++k) { if (arrayNumVector[l] == -1 && statusMap[k].first == -1){//key为-1.说明是一定要划分的 //删除该元素 statusMap[k].first = -2;//-2代表删除状态 tempArray.push_back(statusMap[k].second); break; } else{ if (statusMap[k].first == arrayNumVector[l]){//根据集合序号进行划分 tempArray.push_back(statusMap[k].second); } } } cout << endl; dividedArrays.emplace_back(tempArray, true); } auto iter = dividedArrays.begin()+j; dividedArrays.erase(iter); j--; break;//当前集合结束，调到下一个位置的集合，因为删除了该元素，其他元素前移一位,所以j-- } }//end i if (canNotBeDivided == alphabet.size()){ dividedArrays[j].second = false;//如果一个集合经过转换后还是该集合本身，该集合无需再进行划分 } }//end j //判断是否结束循环，如果划分集合下面的所有集合都不可划分就退出循环 flag = false; for (int m = 0; m < dividedArrays.size(); ++m) { if (dividedArrays[m].second == true){ flag = true; break; } } } //合并DFA等价状态 for (int j1 = 0; j1 < dividedArrays.size(); ++j1) { if (dividedArrays[j1].first.size() > 1){//只要每个集合的大小大于1，说明有需要合并的 int represent = dividedArrays[j1].first[0]; for (int i = 1; i < dividedArrays[j1].first.size(); ++i) {//除了第一个节点，其他节点都和第一个节点合并 mergeTwoNode(represent,dividedArrays[j1].first[i]);//合并这两个节点 } } }}5、生成C语言词法分析程序
程序长这样
开整！
得到了最简DFA后，我们就可以生成C语言词法分析程序了
通过最简DFA，我们可以获得：1、状态数 2、字母表 3、每个状态输入字母表后转换到的位置
根据这些信息，我们就可以生成词法分析程序了！
void Lex::generateCCode(MyGraph myGraph){ string tag1 =" "; string tag2 =" "; string tag3 =" "; string text="#include<stdio.h> \r\n\r\nint main(){\r\n" + tag1 + "int stateID = 1;\r\n" + tag1 + "int toexit = 0;\r\n" + tag1 + "while(!toexit){\r\n" + tag2 + "char ch = gettoken();\r\n" + tag2 + "switch(stateID){ //不可变部分\r\n\r\n" + tag3 + "//可变部分\r\n"; string result = ""; int num = myGraph.mVexNum+1; for(int i = 1; i<num; i ++){ int flag_case=1; int flag_else=0; int flag_elseif = 0; for(int j = 0; j<num; j++){ if (myGraph.getEdgeValue(i,j).at(0) != '^'){ if(flag_case = 1){ result += tag3 + "case " + to_string(i) + ":\r\n"; flag_case = 0; flag_else++; } for (int k = 0; k <myGraph.getEdgeValue(i,j).size() ; ++k) { if(flag_elseif==0){ result += tag3 + "if(ch == " + myGraph.getEdgeValue(i,j).at(k) + ") stateID = " + to_string(j) + ";\r\n"; flag_elseif ++; } else{ result += tag3 + "else if(ch == " + myGraph.getEdgeValue(i,j).at(k) + ") stateID = " + to_string(j) + ";\r\n"; } } } if(flag_else!=0 && j == num-1){ result += tag3 + "else toexit = 1;\r\n" + tag3 + "break;\r\n\r\n"; } } } text += result + tag3 + string("default:\r\n") + tag3 + "toexit = 1;\r\n" + tag3 +"break;\r\n"; text += tag2 + "}\r\n" + tag1 + "}\r\n" "}\r\n";}