J未完成，暂更。
目录
试题 A: 阶乘求和
【问题描述】
【答案提交】
【代码】：
试题 B: 幸运数字
【问题描述】
【答案提交】 答案为：215040
【思路解析】
【代码】
试题 C: 数组分割
【问题描述】
【输入格式】
【输出格式】
【样例输入】
【样例输出】
【样例说明】
【评测用例规模与约定】
【思路分析】
【代码】
试题 D: 矩形总面积
【问题描述】
【输入格式】
【输出格式】
【样例输入】
【样例输出】
【样例说明】
【评测用例规模与约定】
[思路解析】
【代码】
试题 E: 蜗牛
【问题描述】
【输入格式】
【输出格式】
【样例输入】
【样例输出】
【样例说明】
【评测用例规模与约定】
试题 F: 合并区域
【问题描述】
【输入格式】
【输出格式】
【样例输入】
【样例输出】
【样例说明】
试题 G: 买二赠一
【问题描述】
【输入格式】
【输出格式】
【样例输入】
【样例输出】
【样例说明】
【评测用例规模与约定】
【思路分析】
【代码实现】
试题 H: 合并石子
【问题描述】
【输入格式】
【输出格式】
【样例输入】
【样例输出】
【样例说明】
【评测用例规模与约定】
试题 I: 最大开支
【问题描述】
【输入格式】
【输出格式】
【样例输入】
【样例输出】
【样例说明】
【评测用例规模与约定】
【思路解析】
【代码实现】
试题 J: 魔法阵
【问题描述】
【输入格式】
【输出格式】
【样例输入 1】
【样例输出 1】
【样例输入 2】
【样例输出 2】
【样例说明】
【评测用例规模与约定】
试题 A: 阶乘求和
本题总分：5 分
【问题描述】
令 S = 1! + 2! + 3! + ... + 202320232023!，求 S 的末尾 9 位数字。 提示：答案首位不为 0。
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一 个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。
[思路解析]：
分析知，到45之后，每个数都含有这几个因子5 10 15 20 25 30 35 40，与偶数可以凑成0，40! 的末九位数就全都为 0 了，而且我们只求末九位数字，所以40！以后的阶乘对我们就没有影响了。 答案为：420940313
【代码】：
// 这里计算阶乘时使用lang存数据，以防数据过大。
/** * @ProjectName: study3 * @FileName: A * @author:HWJ * @Data: 2023/6/15 21:08 */public class A { public static void main(String[] args) { long total = 0; for (int i = 1; i < 40; i++) { total = (total + factorial(i)) % 1000000000; } System.out.println(total); } public static long factorial(int i){ long t = 1; for (int j = 1; j <= i; j++) { t = (t*j) % 1000000000; } return t; }}试题 B: 幸运数字
本题总分：5 分
【问题描述】
哈沙德数是指在某个固定的进位制当中，可以被各位数字之和整除的正整 数。例如 126 是十进制下的一个哈沙德数，因为 (126)10 mod (1+2+6) = 0；126
也是八进制下的哈沙德数，因为 (126)10 = (176)8，(126)10 mod (1 + 7 + 6) = 0； 同时 126 也是 16 进制下的哈沙德数，因为 (126)10 = (7e)16，(126)10 mod (7 + e) = 0。小蓝认为，如果一个整数在二进制、八进制、十进制、十六进制下均为 哈沙德数，那么这个数字就是幸运数字，第 1 至第 10 个幸运数字的十进制表示 为：1 , 2 , 4 , 6 , 8 , 40 , 48 , 72 , 120 , 126 . . . 。现在他想知道第 2023 个幸运数 字是多少？你只需要告诉小蓝这个整数的十进制表示即可。
【答案提交】 答案为：215040
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一 个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。
【思路解析】
通过模拟这个过程，然后循环遍历，直到找到第2023个幸运数字。
【代码】
/** * @ProjectName: study3 * @FileName: B * @author:HWJ * @Data: 2023/6/15 21:34 */public class B { public static void main(String[] args) { int count = 10; for (int i = 127; ; i++) { if (divide(i, 2) == 0 && divide(i, 8) == 0 && divide(i, 10) == 0 && divide(i, 16) == 0) { count++; if (count == 2023) { System.out.println(i); } } } } public static int divide(int num, int v) { int digits = 0; int n = num; while (num > 0) { digits += num % v; num /= v; } return n % digits; }}试题 C: 数组分割
时间限制: 1.0s 内存限制: 512.0MB 本题总分：10 分
【问题描述】
小蓝有一个长度为 N 的数组 A = [A0, A1, . . . , AN−1]。现在小蓝想要从 A 对 应的数组下标所构成的集合 I = {0, 1, 2, . . . , N − 1} 中找出一个子集 R1，那么 R1
在 I 中的补集为 R2。记 S 1 = ∑
r∈R1 Ar，S 2 = ∑
r∈R2 Ar，我们要求 S 1 和 S 2 均为 偶数，请问在这种情况下共有多少种不同的 R1。当 R1 或 R2 为空集时我们将
S 1 或 S 2 视为 0。
【输入格式】
第一行一个整数 T，表示有 T 组数据。 接下来输入 T 组数据，每组数据包含两行：第一行一个整数 N，表示数组A 的长度；第二行输入 N 个整数从左至右依次为 A0, A1, . . . , AN−1，相邻元素之 间用空格分隔。
【输出格式】
对于每组数据，输出一行，包含一个整数表示答案，答案可能会很大，你 需要将答案对 1000000007 进行取模后输出。
【样例输入】
| 2 |
| 2 |
| 6 6 |
| 2 |
| 1 6 |
【样例输出】
4
0
【样例说明】
对于第一组数据，答案为 4。（注意：大括号内的数字表示元素在数组中的 下标。）
R1 = {0}, R2 = {1}；此时 S 1 = A0 = 6 为偶数, S 2 = A1 = 6 为偶数。
R1 = {1}, R2 = {0}；此时 S 1 = A1 = 6 为偶数, S 2 = A0 = 6 为偶数。
R1 = {0, 1}, R2 = {}；此时 S 1 = A0 + A1 = 12 为偶数, S 2 = 0 为偶数。
R1 = {}, R2 = {0, 1}；此时 S 1 = 0 为偶数, S 2 = A0 + A1 = 12 为偶数。 对于第二组数据，无论怎么选择，都不满足条件，所以答案为 0。
【评测用例规模与约定】
对于 20% 的评测用例，1 ≤ N ≤ 10。 对于 40% 的评测用例，1 ≤ N ≤ 10 2。 对于 100% 的评测用例，1 ≤ T ≤ 10, 1 ≤ N ≤ 10 3 , 0 ≤ Ai ≤ 10 9。
【思路分析】
就是我们需要选择r1包括部分值，r2为剩余值，他们两个均为偶数，当整体和为奇数时，无论如何选择，总有一个为奇数，不满足情况，此组数据返回0，如果当整体和为偶数的时候，我们可以r1选择所有数，然后不断剔除一个任意偶数，或者任意两个奇数，此时就需要将数据按照偶数和奇数分类，计算偶数和奇数个数为偶数even个，奇数odd个，因为偶数和奇数的选择彼此独立，根据乘法法则，总方式为偶数方式*奇数方式。
即（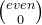
+ 
+ 
+...... + 
) * (
+ 
+ 
+ .... + 
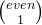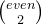
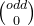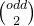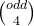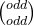) % 1000000007.
由于取余对除法不满足分配律，但是算组合数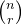
会遇到除法，则我们需要使用费马小定理来解决这个问题。
原理如下：
【代码】
【费马小定理代码】
public static long qpow(long x, long n) { // 快速幂，求 x 的 n 次方 long res = 1; for (; n >= 1; n >>= 1, x = x * x % mod) { if ((n & 1) == 1) { res = res * x % mod; } } return res; } public static long combinatorial(int n, int r) { // 费小马定理 long res = 1; for (int i = 1; i <= n; i++) { res = res * i % mod; } for (int i = 1; i <= r; i++) { res = res * qpow(i, mod - 2) % mod; } for (int i = 1; i <= (n - r); i++) { res = res * qpow(i, mod - 2) % mod; } return res; }【题目代码】
import java.util.Scanner;/** * @ProjectName: study3 * @FileName: C * @author:HWJ * @Data: 2023/6/15 21:57 */public class C { static long mod = 1000000007; public static void main(String[] args) { Scanner input = new Scanner(System.in); int T = input.nextInt(); for (int i = 0; i < T; i++) { int n = input.nextInt(); int[] num = new int[n]; for (int j = 0; j < n; j++) { num[j] = input.nextInt(); } int[] res = classify(num); int odd = res[0]; int even = res[1]; if (odd % 2 != 0) { System.out.println(0); continue; } long ans = 0; for (int j = 0; j <= even; j++) { ans = (ans + combinatorial(even, j)) % mod; } long ans2 = 0; for (int j = 0; j <= odd; j += 2) { ans2 = (ans2 + combinatorial(odd, j)) % mod; } long total = (ans * ans2) % mod; System.out.println(total); } } public static int[] classify(int[] arr) { int odd = 0; // 奇数 int even = 0; // 偶数 for (int i = 0; i < arr.length; i++) { if (arr[i] % 2 == 0) { even++; } else { odd++; } } int[] res = {odd, even}; return res; } public static long qpow(long x, long n) { // 快速幂，求 x 的 n 次方 long res = 1; for (; n >= 1; n >>= 1, x = x * x % mod) { if ((n & 1) == 1) { res = res * x % mod; } } return res; } public static long combinatorial(int n, int r) { // 费小马定理 long res = 1; for (int i = 1; i <= n; i++) { res = res * i % mod; } for (int i = 1; i <= r; i++) { res = res * qpow(i, mod - 2) % mod; } for (int i = 1; i <= (n - r); i++) { res = res * qpow(i, mod - 2) % mod; } return res; }}[代码提交结果】
试题 D: 矩形总面积
时间限制: 1.0s 内存限制: 512.0MB 本题总分：10 分
【问题描述】
平面上有个两个矩形 R1 和 R2，它们各边都与坐标轴平行。设 (x1, y1) 和
(x2, y2) 依次是 R1 的左下角和右上角坐标，(x3, y3) 和 (x4, y4) 依次是 R2 的左下 角和右上角坐标，请你计算 R1 和 R2 的总面积是多少？ 注意：如果 R1 和 R2 有重叠区域，重叠区域的面积只计算一次。
【输入格式】
输入只有一行，包含 8 个整数，依次是：x1，y1，x2，y2，x3，y3，x4 和 y4。
【输出格式】
一个整数，代表答案。
【样例输入】
2 1 7 4 5 3 8 6
【样例输出】
22
【样例说明】
样例中的两个矩形如图所示：
【评测用例规模与约定】
对于 20% 的数据，R1 和 R2 没有重叠区域。 对于 20% 的数据，其中一个矩形完全在另一个矩形内部。 对于 50% 的数据，所有坐标的取值范围是 [0, 10^3]。 对于 100% 的数据，所有坐标的取值范围是 [0, 10^5]。
[思路解析】
先计算两个矩形的面积，然后将其相加，如果重叠然后就减去重叠区域的面积，否则直接返回，所以需要写一个判断是否重叠的函数，此时求他们在x轴和y轴上的交集。
【代码】
import java.util.Scanner;/** * @ProjectName: study3 * @FileName: D * @author:HWJ * @Data: 2023/6/15 22:57 */public class D { public static void main(String[] args) { Scanner input = new Scanner(System.in); long x1 = input.nextInt(); long y1 = input.nextInt(); long x2 = input.nextInt(); long y2 = input.nextInt(); long x3 = input.nextInt(); long y3 = input.nextInt(); long x4 = input.nextInt(); long y4 = input.nextInt(); long s = (x2 - x1) * (y2 - y1) + (x4 - x3) * (y4 - y3); // 这里的数据需要用long类型，防止储存不下 s = s - check(x1, y1, x2, y2, x3, y3, x4, y4); System.out.println(s); } public static long check(long x1, long y1, long x2, long y2, long x3, long y3, long x4, long y4){ long x = 0; // 如果没找到交集，设置为0，可以直接赋初值为0，然后只用找交集 long y = 0; if (x1 > x3 && x1 < x4){ // 这里寻找x的交集区域 x = x2 < x4? (x2 - x1):(x4 - x1); }else if (x2 > x3 && x2 < x4){ x = x1 > x3? (x2 - x1):(x2 - x3); } if (y1 > y3 && y1 < y4){ // 这里寻找y的交集区域 y = y2 < y4? (y2 - y1):(y4 - y1); }else if (y2 > y3 && y2 < y4){ y = y1 > y3? (y2 - y1):(y2 - y3); } if (x == 0){ // 第一个矩形如果不在第二个矩形内部或者相交，考虑是否存在第二个矩形在第一个矩形内部的情况 if (x3 > x1 && x3 < x2){ // 这里寻找x的交集区域 x = x4 < x2? (x4 - x3):(x2 - x3); }else if (x4 > x1 && x4 < x2){ x = x3 > x1? (x4 - x3):(x3 - x2); } } if (y == 0){ if (y3 > y1 && y3 < y2){ // 这里寻找x的交集区域 y = y4 < y2? (y4 - y3):(y2 - y3); }else if (y4 > y1 && y4 < y2){ y = y3 > y1? (y4 - y3):(y3 - y2); } } return x*y; }}[代码提交结果】
试题 E: 蜗牛
时间限制: 1.0s 内存限制: 512.0MB 本题总分：15 分
【问题描述】
这天，一只蜗牛来到了二维坐标系的原点。 在 x 轴上长有 n 根竹竿。它们平行于 y 轴，底部纵坐标为 0，横坐标分别 为 x1, x2, ..., xn。竹竿的高度均为无限高，宽度可忽略。蜗牛想要从原点走到第n 个竹竿的底部也就是坐标 (xn, 0)。它只能在 x 轴上或者竹竿上爬行，在 x 轴 上爬行速度为 1 单位每秒；由于受到引力影响，蜗牛在竹竿上向上和向下爬行 的速度分别为 0.7 单位每秒和 1.3 单位每秒。 为了快速到达目的地，它施展了魔法，在第 i 和 i + 1 根竹竿之间建立了传 送门（0 < i < n），如果蜗牛位于第 i 根竹竿的高度为 ai 的位置 (xi , ai)，就可以 瞬间到达第 i + 1 根竹竿的高度为 bi+1 的位置 (xi+1, bi+1)，请计算蜗牛最少需要 多少秒才能到达目的地。
【输入格式】
输入共 1 + n 行，第一行为一个正整数 n； 第二行为 n 个正整数 x1, x2, . . . , xn； 后面 n − 1 行，每行两个正整数 ai , bi+1。
【输出格式】
输出共一行，一个浮点数表示答案（四舍五入保留两位小数）。
【样例输入】
3
1 10 11
1 1
2 1
【样例输出】
4.20
【样例说明】
蜗牛路线：
(0, 0) → (1, 0) → (1, 1) → (10, 1) → (10, 0) → (11, 0)，花费时间为 1 + 1 /0.7 + 0 + 1 /1.3 + 1 ≈ 4.20
【评测用例规模与约定】
对于 20% 的数据，保证 n ≤ 15； 对于 100% 的数据，保证 n ≤10^5 ，ai , bi ≤ 10^4，xi ≤ 10^9。
【思路解析】
你从第一杆走到第3杆所用的方式，并不会对后面用时产生影响，走到下一杆至于当前杆的状态有关，所以每走一杆就找到走到这个地方的最短时间，然后不断往后动态规划，就找到了最优时间。
【代码】
import java.util.Scanner;/** * @ProjectName: study3 * @FileName: E * @author:HWJ * @Data: 2023/6/16 15:49 */public class E { public static void main(String[] args) { Scanner input = new Scanner(System.in); int n = input.nextInt(); int[] num = new int[n+1]; int[][] ab = new int[n+1][2]; for (int i = 1; i <= n; i++) { num[i] = input.nextInt(); } for (int i = 1; i <= n-1; i++) { ab[i][0] = input.nextInt(); ab[i][1] = input.nextInt(); } double[][] dp = new double[n+1][2]; // 这里使用动态规划，因为你到下一个杆，要么传送，要么直行。 dp[1][0] = num[1]; // 直行 dp[1][1] = num[1] + ab[1][0] / 0.7; // 传送 for (int i = 2; i <= n; i++) { // 直行 如果上一次为直行，那这次继续直行 如果上一次为传送，那就从杆上下来 找这两个情况那个用时最短 dp[i][0] = Math.min(dp[i-1][0] + num[i] - num[i-1], dp[i-1][1] + ab[i-1][1] / 1.3); // 传送 如果上一次为直行，那这次上杆 如果上一次为传送，那就从杆上找到这次传送的传送点，然后到这里去 找这两个情况那个用时最短 dp[i][1] = Math.min(dp[i][0] + ab[i][0] / 0.7, dp[i-1][1] + (ab[i-1][1] < ab[i][0] ? (ab[i][0] - ab[i-1][1])/0.7:(ab[i-1][1] - ab[i][0])/1.3)); } System.out.printf("%.2f", dp[n][0]); }}[代码提交结果】
试题 F: 合并区域
时间限制: 2.0s 内存限制: 512.0MB 本题总分：15 分
【问题描述】
小蓝在玩一款种地游戏。现在他被分配给了两块大小均为 N × N 的正方形 区域。这两块区域都按照 N × N 的规格进行了均等划分，划分成了若干块面积 相同的小区域，其中每块小区域要么是岩石，要么就是土壤，在垂直或者水平 方向上相邻的土壤可以组成一块土地。现在小蓝想要对这两块区域沿着边缘进 行合并，他想知道合并以后可以得到的最大的一块土地的面积是多少（土地的 面积就是土地中土壤小区域的块数）？ 在进行合并时，小区域之间必须对齐。可以在两块方形区域的任何一条边 上进行合并，可以对两块方形区域进行 90 度、180 度、270 度、360 度的旋转， 但不可以进行上下或左右翻转，并且两块方形区域不可以发生重叠。
【输入格式】
第一行一个整数 N 表示区域大小。 接下来 N 行表示第一块区域，每行 N 个值为 0 或 1 的整数，相邻的整数 之间用空格进行分隔。值为 0 表示这块小区域是岩石，值为 1 表示这块小区域 是土壤。 再接下来 N 行表示第二块区域，每行 N 个值为 0 或 1 的整数，相邻的整 数之间用空格进行分隔。值为 0 表示这块小区域是岩石，值为 1 表示这块小区 域是土壤。
【输出格式】
一个整数表示将两块区域合并之后可以产生的最大的土地面积。
【样例输入】
4
0 1 1 0
1 0 1 1
1 0 1 0
1 1 1 0
0 0 1 0
0 1 1 0
1 0 0 0
1 1 1 1
【样例输出】
15
【样例说明】
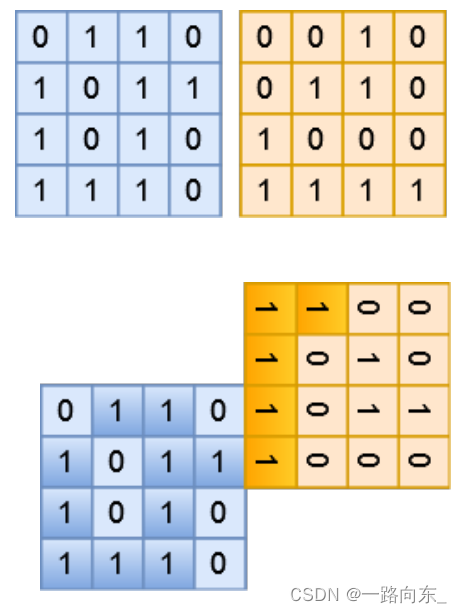
第一张图展示了样例中的两块区域的布局。第二张图展示了其中一种最佳 的合并方式，此时最大的土地面积为 15。
【评测用例规模与约定】
对于 30% 的数据，1 ≤ N ≤ 5。 对于 60% 的数据，1 ≤ N ≤ 15。 对于 100% 的数据，1 ≤ N ≤ 50。
【思路解析】
这道题没有较好的算法实现，但是容易想到可以使用暴力解决，即围绕一个表建立一张地图。暴力求解，遍历至多4*4*50=800次。所以不会超时.
[代码实现】
import java.util.Scanner;/** * @ProjectName: study3 * @FileName: F * @author:HWJ * @Data: 2023/8/31 17:44 */public class F { public static int[][] map; public static int[][] change; public static boolean[][] f; public static int n, x1, y1, x2, y2, ans; // x1, y1 当前地图左上角位置 x2, y2 当前地图右下角位置 public static void main(String[] args) { Scanner input = new Scanner(System.in); n = input.nextInt(); map = new int[300][300]; change = new int[55][55]; f = new boolean[300][300]; ans = 0; for (int i = 60; i <60 + n; i++) { for (int j = 60; j <60 + n; j++) { // 将第一块区域的左上角固定到(60, 60)的位置上。 map[i][j] = input.nextInt(); } } for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { change[i][j] = input.nextInt(); } } solve(); System.out.println(ans); } public static void solve() { // 上 for (int i = 60 - n + 1; i <= 60 + n - 1; i++) { // 变化区域左上角的变动范围 for (int j = 0; j < 4; j++) { x1 = 60 - n; y1 = Math.min(60, i); x2 = 60 + n - 1; y2 = Math.max(60 + n - 1, i + n - 1); add(x1, i, j); ans = Math.max(work(), ans); clear(x1, i); } } for (int i = 60 - n + 1; i <= 60 + n - 1; i++) { //下 for (int j = 0; j < 4; j++) { x1 = 60; y1 = Math.min(60, i); x2 = 60 + 2 * n - 1; y2 = Math.max(60 + n - 1, i + n - 1); add(60 + n, i, j); ans = Math.max(work(), ans); clear(60 + n, i); } } for (int i = 60 - n + 1; i <= 60 + n - 1; i++) { //左 for (int j = 0; j < 4; j++) { x1 = Math.min(i, 60); y1 = 60 - n; x2 = Math.max(i + n - 1, 60 + n - 1); y2 = 60 + n - 1; add(i, y1, j); ans = Math.max(work(), ans); clear(i, y1); } } for (int i = 60 - n + 1; i <= 60 + n - 1; i++) { //右 for (int j = 0; j < 4; j++) { x1 = Math.min(i, 60); y1 = 60; x2 = Math.max(i + n - 1, 60 + n - 1); y2 = 60 + 2 * n - 1; add(i, 60 + n, j); ans = Math.max(work(), ans); clear(i, 60 + n); } } } static void add(int a, int b, int op) { if (op == 0) { for (int i = a; i < a + n; i++) for (int j = b; j < b + n; j++) map[i][j] = change[i - a][j - b]; } else if (op == 1) { //逆时针1次 for (int j = b, u = 0; j < b + n; j++, u++) for (int i = a + n - 1, v = 0; i >= a; i--, v++) map[i][j] = change[u][v]; } else if (op == 2) { //顺时针1次 for (int j = b + n - 1, u = 0; j >= b; j--, u++) for (int i = a, v = 0; i < a + n; i++, v++) map[i][j] = change[u][v]; } else { //倒置 for (int i = a + n - 1, u = 0; i >= a; i--, u++) for (int j = b + n - 1, v = 0; j >= b; j--, v++) map[i][j] = change[u][v]; } } public static int work() { int res = 0; for (int u = x1; u <= x2; u++) for (int v = y1; v <= y2; v++) f[u][v] = false; for (int i = x1; i <= x2; i++) { for (int j = y1; j <= y2; j++) { if (map[i][j] == 1 && !f[i][j]) { res = Math.max(infect(i, j), res); } } } return res; } public static int infect(int i, int j) { if (!(i >= x1 && i <= x2 && j >= y1 && j <= y2 && !f[i][j] && map[i][j] == 1)) { return 0; } f[i][j] = true; return 1 + infect(i + 1, j) + infect(i - 1, j) + infect(i, j + 1) + infect(i, j - 1); } public static void clear(int a, int b) { for (int i = a; i < a + n; i++){ for (int j = b; j < b + n; j++){ map[i][j] = 0; } } }}【代码提交结果】
试题 G: 买二赠一
时间限制: 1.0s 内存限制: 512.0MB 本题总分：20 分
【问题描述】
某商场有 N 件商品，其中第 i 件的价格是 Ai。现在该商场正在进行 “买二 赠一” 的优惠活动，具体规则是： 每购买 2 件商品，假设其中较便宜的价格是 P（如果两件商品价格一样， 则 P 等于其中一件商品的价格），就可以从剩余商品中任选一件价格不超过 P/2的商品，免费获得这一件商品。可以通过反复购买 2 件商品来获得多件免费商品，但是每件商品只能被购买或免费获得一次。 小明想知道如果要拿下所有商品（包含购买和免费获得），至少要花费多少 钱？
【输入格式】
第一行包含一个整数 N。 第二行包含 N 个整数，代表 A1, A2, A3, . . . ，AN。
【输出格式】
输出一个整数，代表答案。
【样例输入】
7
1 4 2 8 5 7 1
【样例输出】
25
【样例说明】
小明可以先购买价格 4 和 8 的商品，免费获得一件价格为 1 的商品；再后 买价格为 5 和 7 的商品，免费获得价格为 2 的商品；最后单独购买剩下的一件 价格为 1 的商品。总计花费 4 + 8 + 5 + 7 + 1 = 25。不存在花费更低的方案。
【评测用例规模与约定】
对于 30% 的数据，1 ≤ N ≤ 20。 对于 100% 的数据，1 ≤ N ≤ 5 × 10^5，1 ≤ Ai ≤10^9 。
【思路分析】
我们每次购买时，先购买此时最大的和次大的商品，然后我们就可以得到一个较大的免费机会，然后将这个免费机会放入一个队列中，再下一次购买商品时，判断是否能够免费获得商品。
提示：用于获得免费机会的两个商品，必须支付现金，不能对这两个商品使用免费机会。
【代码实现】
import java.util.*;/** * @ProjectName: study3 * @FileName: G * @author:HWJ * @Data: 2023/6/16 8:13 */public class G { public static void main(String[] args) { Scanner input = new Scanner(System.in); int n = input.nextInt(); long[] num = new long[n]; for (int i = 0; i < n; i++) { num[i] = input.nextInt(); } Arrays.sort(num); int p = n - 1; long total = 0; LinkedList<Long> free = new LinkedList<>(); while (p >= 0) { while (!free.isEmpty() && p >= 0) { if (free.peek() >= num[p]) { p--; free.poll(); }else { break; } } if (p >= 0) { total += num[p]; p--; } while (!free.isEmpty() && p >= 0) { if (free.peek() >= num[p]) { p--; free.poll(); }else { break; } } if (p >= 0) { total += num[p]; free.add(num[p] / 2); p--; } } System.out.println(total); }}[代码 提交结果】
试题 H: 合并石子
时间限制: 1.0s 内存限制: 512.0MB 本题总分：20 分
【问题描述】
在桌面从左至右横向摆放着 N 堆石子。每一堆石子都有着相同的颜色，颜 色可能是颜色 0，颜色 1 或者颜色 2 中的其中一种。 现在要对石子进行合并，规定每次只能选择位置相邻并且颜色相同的两堆 石子进行合并。合并后新堆的相对位置保持不变，新堆的石子数目为所选择的 两堆石子数目之和，并且新堆石子的颜色也会发生循环式的变化。具体来说： 两堆颜色 0 的石子合并后的石子堆为颜色 1，两堆颜色 1 的石子合并后的石子 堆为颜色 2，两堆颜色 2 的石子合并后的石子堆为颜色 0。本次合并的花费为所 选择的两堆石子的数目之和。 给出 N 堆石子以及他们的初始颜色，请问最少可以将它们合并为多少堆石 子？如果有多种答案，选择其中合并总花费最小的一种，合并总花费指的是在 所有的合并操作中产生的合并花费的总和。
【输入格式】
第一行一个正整数 N 表示石子堆数。 第二行包含 N 个用空格分隔的正整数，表示从左至右每一堆石子的数目。 第三行包含 N 个值为 0 或 1 或 2 的整数表示每堆石头的颜色。
【输出格式】
一行包含两个整数，用空格分隔。其中第一个整数表示合并后数目最少的 石头堆数，第二个整数表示对应的最小花费。
【样例输入】
5
5 10 1 8 6
1 1 0 2 2
【样例输出】
2 44
【样例说明】
上图显示了两种不同的合并方式。其中节点中标明了每一堆的石子数目， 在方括号中标注了当前堆石子的颜色属性。左图的这种合并方式最终剩下了两 堆石子，所产生的合并总花费为 15 + 14 + 15 = 44；右图的这种合并方式最终 也剩下了两堆石子，但产生的合并总花费为 14 + 15 + 25 = 54。综上所述，我 们选择合并花费为 44 的这种方式作为答案。
【评测用例规模与约定】
对于 30% 的评测用例，1 ≤ N ≤ 10。 对于 50% 的评测用例，1 ≤ N ≤ 50。 对于 100% 的评测用例，1 ≤ N ≤ 300, 1 ≤ 每堆石子的数目 ≤ 1000。
【思路解析】
这里因为是多组不同颜色的石子进行合并一直合并到无法下一次操作时最少能剩下多少堆石子，并且在次情况下最少花费多少。
因为需要尽量少的花费，且要相同的颜色才能进行合并，那么可以通过选择区间合并来进行计算这个区间合并成一个颜色的石堆需要多少花费。得到每个区间的合并答案时，再通过Floyd算法来计算怎样选择区间可以使得最后合并出来的石堆数最少。
【代码实现】
import java.io.*;import java.util.*;public class Main{ static int maxn = 200005,n,m,inf=(int)1e9; static long INF = (long)2e18,ans = 0,mod = (int)1e9+7; static Scanner sc = new Scanner (System.in); static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in)); static StreamTokenizer st =new StreamTokenizer(bf); static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out)); public static void main(String[]args) throws IOException{ int T = 1; while(T-->0) solve(); pw.flush(); } static final int I() throws IOException { st.nextToken(); return (int)st.nval; } static int dp[][][] = new int [303][303][3]; static int num[][] = new int [303][303]; static int a[] = new int [301]; static int sum[] = new int [301]; //前缀和 static int c[] = new int [301]; static int cost[][] = new int [303][303]; static void solve() throws IOException{ n= I(); for(int i=1;i<=n;i++) for(int j=i;j<=n;j++) { num[i][j]=j-i+1; for(int k=0;k<3;k++) dp[i][j][k]=inf; } for(int i=1;i<=n;i++) a[i] = I(); for(int i=1;i<=n;i++) sum[i]=a[i]+sum[i-1]; //前缀和，方便统计区间 for(int i=1;i<=n;i++) c[i] = I();//颜色 for(int i=1;i<=n;i++) dp[i][i][c[i]] = 0; //初始石子堆花费显然为0 for(int len=1;len<=n;len++) for(int i=1;i+len-1<=n;i++) { int j=i+len-1; for(int col=0;col<3;col++) { int min = inf; for(int k=i;k<j;k++) { if(dp[i][k][col]!=inf && dp[k+1][j][col]!=inf) { min = Math.min(min, dp[i][k][col] + dp[k+1][j][col]); } } if(min==inf) continue; num[i][j]=1; dp[i][j][(col+1)%3] = Math.min(dp[i][j][(col+1)%3], min+sum[j]-sum[i-1]); } } for(int i=1;i<=n;i++) for(int j=i;j<=n;j++) if(num[i][j] == 1) cost[i][j] = Math.min(dp[i][j][0], Math.min(dp[i][j][1], dp[i][j][2])); for(int k=1;k<=n;k++) //类似floyd计算花费 for(int i=1;i<=k;i++) for(int j=k+1;j<=n;j++) { if(num[i][j] > num[i][k] + num[k+1][j]) { num[i][j] = num[i][k] + num[k+1][j]; cost[i][j] = cost[i][k]+cost[k+1][j]; } else if(num[i][j] == num[i][k] + num[k+1][j]) { cost[i][j] = Math.min(cost[i][j], cost[i][k]+cost[k+1][j]); } } pw.println(num[1][n]+" "+cost[1][n]); }}【代码提交结果】
试题 I: 最大开支
时间限制: 1.0s 内存限制: 512.0MB 本题总分：25 分
【问题描述】
小蓝所在学校周边新开业了一家游乐园，小蓝作为班长，打算组织大家去 游乐园玩。已知一共有 N 个人参加这次活动，游乐园有 M 个娱乐项目，每个 项目都需要买门票后才可进去游玩。门票的价格并不是固定的，团购的人越多 单价越便宜，当团购的人数大于某个阈值时，这些团购的人便可以免费进入项 目进行游玩。这 M 个娱乐项目是独立的，所以只有选择了同一个项目的人才可 以参与这个项目的团购。第 i 个项目的门票价格 Hi 与团购的人数 X 的关系可 以看作是一个函数：
Hi(X) = max(Ki × X + Bi , 0)
max 表示取二者之中的最大值。当 Hi = 0 时说明团购人数达到了此项目的 免单阈值。 这 N 个人可以根据自己的喜好选择 M 个娱乐项目中的一种，或者有些人 对这些娱乐项目都没有兴趣，也可以选择不去任何一个项目。每个人最多只会 选择一个娱乐项目，如果多个人选择了同一个娱乐项目，那么他们都将享受对 应的团购价格。小蓝想知道他至少需要准备多少钱，使得无论大家如何选择， 他都有能力支付得起所有 N 个人购买娱乐项目的门票钱。
【输入格式】
第一行两个整数 N、M，分别表示参加活动的人数和娱乐项目的个数。 接下来 M 行，每行两个整数，其中第 i 行为 Ki、Bi，表示第 i 个游乐地点 的门票函数中的参数。
【输出格式】
一个整数，表示小蓝至少需要准备多少钱，使得大家无论如何选择项目， 自己都支付得起。
【样例输入】
4 2
-4 10
-2 7
【样例输出】
12
【样例说明】
样例中有 4 个人，2 个娱乐项目，我们用一个二元组 (a, b) 表示 a 个人选 择了第一个娱乐项目，b 个人选择了第二个娱乐项目，那么就有 4 − a − b 个 人没有选择任何项目，方案 (a, b) 对应的门票花费为 max(−4 × a + 10, 0) × a + max(−2 × b + 7, 0) × b，所有的可能如下所示：
a b 花费
0 0 0
0 1 5
0 2 6
0 3 3
0 4 0
1 0 6
1 1 11
1 2 12
1 3 9
2 0 4
2 1 9
2 2 10
3 0 0
3 1
5
4 0 0
其中当 a = 1, b = 2 时花费最大，为 12。此时 1 个人去第一个项目，所以
第一个项目的单价为 10 − 4 = 6，在这个项目上的花费为 6 × 1 = 6；2 个人去 第二个项目，所以第二个项目得单价为 7 − 2 × 2 = 3，在这个项目上的花费为
2 × 3 = 6；还有 1 个人没去任何项目，不用统计；总花费为 12，这是花费最大 的一种方案，所以答案为 12。
【评测用例规模与约定】
对于 30% 的评测用例，1 ≤ N, M ≤ 10。 对于 50% 的评测用例，1 ≤ N, M ≤ 1000。 对于 100% 的评测用例，1 ≤ N, M, Bi ≤ 10^5，− 10^5≤ Ki < 0。
【思路解析】
贪心策略 + 优先队列
第一步：找出所有项目的最大花费时的人数，因为 k为负，b为正，容易知道这是一个开口向下的一元二次曲线，所以可知对称轴x = -b/(2*k)，因为只能取整数，不难知道最大的人数为x或者x+1.
第二步：对于所有人进行贪心策略，在已经安排了x个人的情况下，考虑x+1去那里会让价值变得更高，就安排他去哪里。对于m个项目，在未达到最大人数时可以往这个项目里添加人，如果都达到了最大人数，则结束。
第三步：如何找到价值最高的项目，优先队列实现大根堆，堆顶就是最优项目。
【代码实现】
import java.util.Comparator;import java.util.PriorityQueue;import java.util.Scanner;/** * @ProjectName: study3 * @FileName: I * @author:HWJ * @Data: 2023/6/16 8:45 */public class I { public static void main(String[] args) { Scanner input = new Scanner(System.in); int n = input.nextInt(); int m = input.nextInt(); int[] peoples = new int[m]; // 每个项目最大人数 int[] k = new int[m]; int[] b = new int[m]; int[] s = new int[m]; for (int i = 0; i < m; i++) { k[i] = input.nextInt(); b[i] = input.nextInt(); } for (int i = 0; i < m; i++) { peoples[i] = searchMax(k[i], b[i]); } PriorityQueue<int[]> p = new PriorityQueue<>(new Comparator<int[]>() { @Override public int compare(int[] o1, int[] o2) { return o2[0] - o1[0]; } }); long total = 0; for (int i = 0; i < m; i++) { p.add(new int[]{b[i] + k[i], i}); } for (int i = 0; i < n; i++) { if (p.isEmpty()) { break; } int[] node = p.poll(); total += node[0]; node[0] = node[0] + 2 * k[node[1]]; if (node[0] > 0) { p.add(node); } } System.out.println(total); } public static int searchMax(int k, int b) { int x = b / (-2 * k); return (long) k * x * x + (long) b * x >= (long) k * (x + 1) * (x + 1) + (long) b * (x + 1) ? x : x + 1; }}【代码提交结果】
试题 J: 魔法阵
时间限制: 1.0s 内存限制: 512.0MB 本题总分：25 分
【问题描述】
魔法师小蓝为了营救自己的朋友小 Q，来到了敌人布置的魔法阵。魔法阵 可以看作是一幅具有 N 个结点 M 条边的无向图，结点编号为 0, 1, 2, . . . , N − 1， 图中没有重边和自环。敌人在每条边上都布置了陷阱，每条边都有一个伤害属 性 w，每当小蓝经过一条边时就会受到这条边对应的 w 的伤害。小蓝从结点 0
出发，沿着边行走，想要到达结点 N − 1 营救小 Q。 小蓝有一种特殊的魔法可以使用，假设一条路径按照顺序依次经过了以下
L 条边：e1, e2, . . . , eL（可以出现重复的边），那么期间小蓝受到的总伤害就是
P = ∑L i=1 w(ei)，w(ei) 表示边 ei 的伤害属性。如果 L ≥ K，那么小蓝就可以从 这 L 条边当中选出连续出现的 K 条边 ec , ec+1, . . . , ec+K−1 并免去在这 K 条边行 走期间所受到的伤害，即使用魔法之后路径总伤害变为 P ′ = P − ∑c+K−1
i=c w(ei)。 注意必须恰好选出连续出现的 K 条边，所以当 L < K 时无法使用魔法。 小蓝最多只可以使用一次上述的魔法，请问从结点 0 出发到结点 N − 1 受 到的最小伤害是多少？题目保证至少存在一条从结点 0 到 N − 1 的路径。
【输入格式】
第一行输入三个整数，N, K, M，用空格分隔。 接下来 M 行，每行包含三个整数 u, v,w，表示结点 u 与结点 v 之间存在一 条伤害属性为 w 的无向边。
【输出格式】
输出一行，包含一个整数，表示小蓝从结点 0 到结点 N − 1 受到的最小伤 害。
【样例输入 1】
4 2 3
0 1 2
1 2 1
2 3 4
【样例输出 1】
2
【样例输入 2】
2 5 1
0 1 1
【样例输出 2】
0
【样例说明】
样例 1，存在路径：0 → 1 → 2 → 3，K = 2，如果在 0 → 1 → 2 上使用魔 法，那么答案就是 0 + 0 + 4 = 4；如果在 1 → 2 → 3 上使用魔法，那么答案就 是 2 + 0 + 0 = 2。再也找不到比 2 还小的答案了，所以答案就是 2。 样例 2，存在路径：0 → 1 → 0 → 1 → 0 → 1，K = 5，这条路径总计恰好 走了 5 条边，所以正好可以用魔法消除所有伤害，答案是 0。
【评测用例规模与约定】
对于 30% 的评测用例，1 ≤ N ≤ 20。 对于 50% 的评测用例，1 ≤ N ≤ 100。 对于 100% 的评测用例，1 ≤ N ≤ 1000, 1 ≤ M ≤ N×(N−1)/2 ，1 ≤ K ≤ 10, 0 ≤ u, v ≤ N − 1，1 ≤ w ≤ 1000。