目录
摘要:
1.K-means算法
2.Calinski-Harabasz Criterion(卡林斯基-哈拉巴斯指标,CH值)
3.Davies-Bouldin Criterion(戴维斯-博尔丁指标,DB值)
4.Gap Value(Gap值)
5.Silhouette Coefficient(轮廓系数)
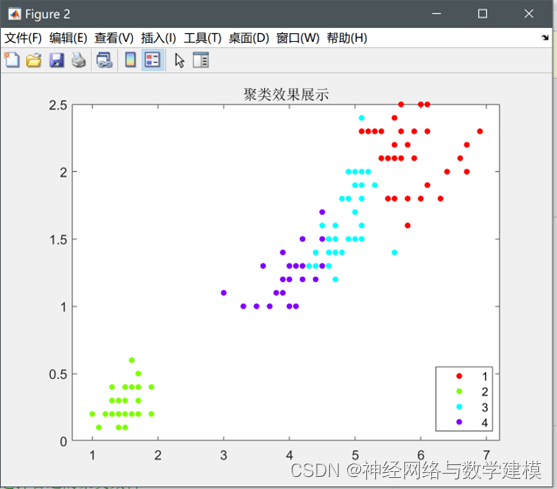
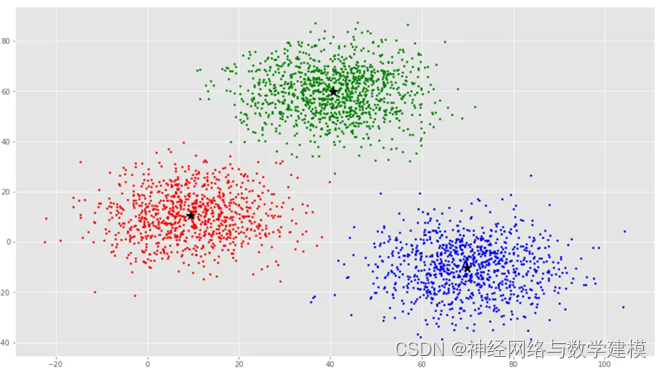
6.基于Matlab的K-means聚类及最佳聚类数选取结果:
7.本文Matlab代码实现:
摘要:
Kmeans算法中,K值所决定的是在该聚类算法中,所要分配聚类的簇的多少。Kmeans算法对初始值是⽐较敏感的,对于同样的k值,选取的点不同,会影响算法的聚类效果和迭代的次数。本文通过计算原始数据中的:CH值、DB值、Gap值、轮廓系数,四种指标来衡量K-means的最佳聚类数目,并使用K-means进行聚类,最后可视化聚类的结果。
本文代码已做标准化处理,导入自己数据即可使用,十分方便
通过该代码即可确定最佳的聚类个数,适合数学建模等应用
1.K-means算法
k均值聚类算法(k-means clustering algorithm)是一种迭代求解的聚类分析算法,其步骤是,预将数据分为K组,则随机选取K个对象作为初始的聚类中心,然后计算每个对象与各个种子聚类中心之间的距离,把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本,聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有(或最小数目)对象被重新分配给不同的聚类,没有(或最小数目)聚类中心再发生变化,误差平方和局部最小。
K-means的计算步骤:

2.Calinski-Harabasz Criterion(卡林斯基-哈拉巴斯指标,CH值)
卡林斯基-哈拉巴斯准则有时被称为方差比准则(VRC)。卡林斯基-哈拉巴斯指数定义为
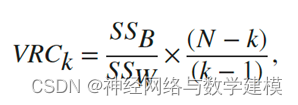
其中,SSB是总体簇间方差,SSW是总体簇内方差,k是簇数,N是观测数。
定义良好的簇具有较大的簇间方差(SSB)和较小的簇内方差(SSW)。VRCk比率越大,数据分区越好。要确定最佳聚类数,最大化关于k的VRCk。最佳聚类数对应于具有最高卡林斯基-哈拉巴斯指数值的解。
卡林斯基-哈拉巴斯准则最适合于具有平方欧几里德距离的k均值聚类解。
3.Davies-Bouldin Criterion(戴维斯-博尔丁指标,DB值)
Davies-Bouldin 准则基于聚类内距离和聚类间距离的比率。戴维斯-博尔丁指数定义为:
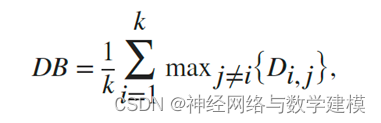
其中,Di,j是第i个和第j个簇的簇内到簇间距离比。在数学上:
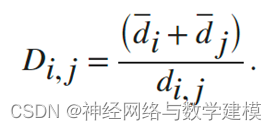
di是第i个簇中每个点与第i个簇的质心之间的平均距离。dj是第j个簇中每个点与第j个簇的质心之间的平均距离。dij是第i个和第j个簇的质心之间的欧氏距离Dij的最大值表示簇i的最坏簇内-簇间比率。最优聚类解决方案具有最小的Davies Bouldin指数值。
4.Gap Value(Gap值)
一个常见的聚类评估的图形方法是将误差测量值与几个建议的聚类数量作对比,并找出这个图形的 "肘部"。肘部 "出现在误差测量的最大幅度下降处。差距标准通过将 "肘部 "的位置估计为具有最大差距值的聚类的数量来正式确定这一方法。因此,在差距准则下,最佳的集群数量对应于在一个容忍范围内具有最大的局部或整体差距值的解决方案。具体公式如下:

其中,n是样本量,k是被评估的聚类数量,Wk是聚类内分散度的集合测量。
5.Silhouette Coefficient(轮廓系数)
每个点的轮廓系数是衡量该点与同一聚类中的其他点的相似程度,与其他聚类的点相比。第i个点的轮廓系数si定义为:

其中,ai是第i个点到与i相同聚类中其他点的平均距离,bi是第i个点到不同聚类中的点的最小平均距离,在聚类中最小。如果第i点是其聚类中唯一的点,那么轮廓系数si被设置为1。轮廓系数的范围从-1到1。一个高的轮廓系数表明该点与它自己的聚类匹配良好,而与其他聚类匹配较差。如果大多数点有一个高的轮廓系数,那么聚类方案是合适的。如果许多点的轮廓系数较低或为负值,那么聚类方案可能有太多或太少的聚类。可以用轮廓系数作为任何距离指标的聚类评估标准。
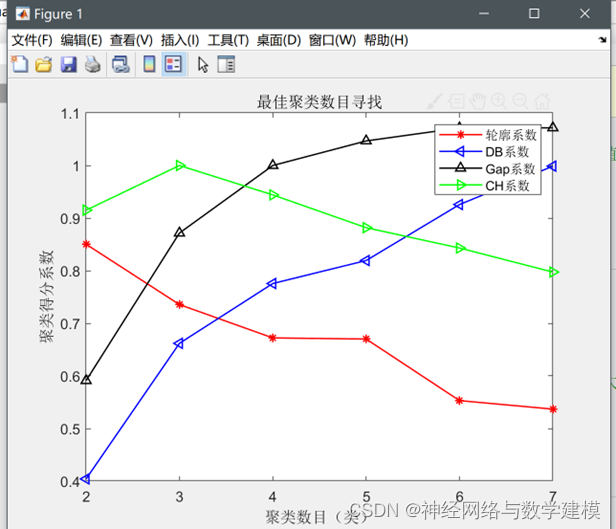
6.基于Matlab的K-means聚类及最佳聚类数选取结果:
各种指标评价图像:
通过该程序即可选取最适合的K-means聚类数目
K-means聚类结果可视化: