接之前写的使用matlab进行二维环境中的路径规划:
在matlab中使用A*算法进行二维路径规划_matlab 路径规划-CSDN博客 https://blog.csdn.net/qq_63079839/article/details/132817790 本文基于城市低空物流无人机作业的背景,进行三维环境建模和算法改进,以之前二维路径规划的内容为基础,做适量改动,并结合实际对算法进行改进。
https://blog.csdn.net/qq_63079839/article/details/132817790 本文基于城市低空物流无人机作业的背景,进行三维环境建模和算法改进,以之前二维路径规划的内容为基础,做适量改动,并结合实际对算法进行改进。
一、三维环境的创建
1、作三维环境图并保存三维数组
不同于二维环境创建时的先创建数组后作图的思路,我在三维建模时采用的是先作图,再将图中将展示的模拟建筑物的障碍数据存入三维数组中,以待后续规划时调用。
这里确实琢磨了挺久,创建三维数据不难,难的是我想要以柱状图的形式将障碍物画出来,没有找到类似的案例和资源,于是自己使用stem3()函数非常朴素的做出了类似效果,如下图所示,分别为三维整体效果图以及俯视图。
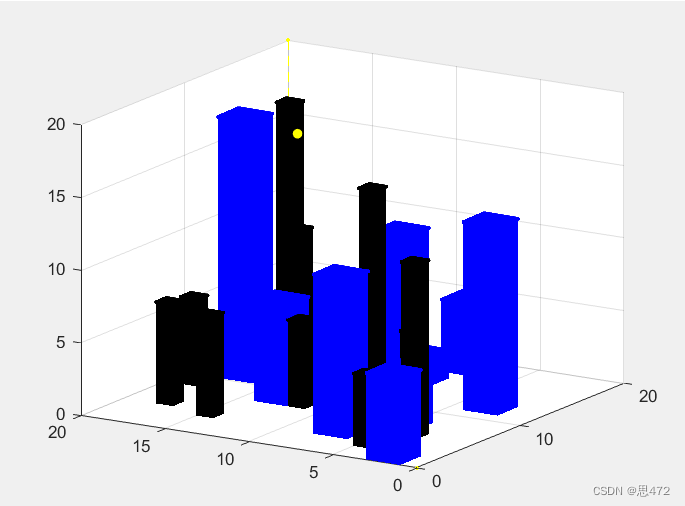
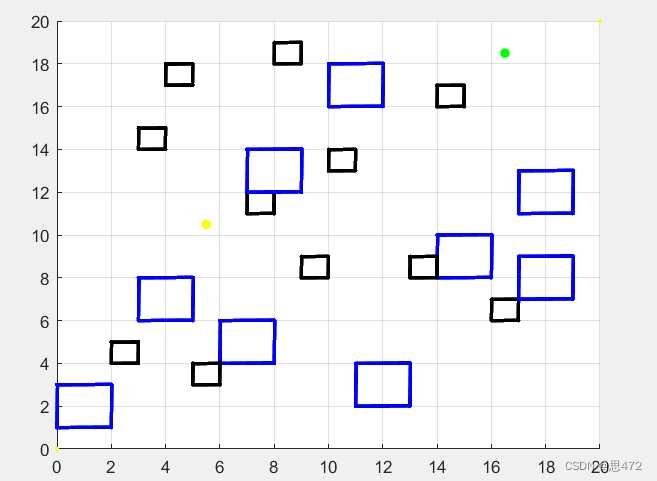
包括三维坐标轴的建立,都只做到了“乍看合理”的程度,比如在(20,20)处会有一根实线,没想到办法让它消失就将它画成了黄色,让那根线看起来不明显。实际上没有做到完美符合我们实际作图的习惯,有读者看完这篇有新的思路或者又做出了改进也欢迎和我交流讨论!
%% 绘制障碍建筑物,并将障碍物位置保存至三维数组field中n=20; %三维地图的边长 field=ones(n,n,n); %地图上的0-n,按方格计数,一共n*n个方格 field(:)=1;% stem3(field,'--.y'); field_x = 0:n:n; field_y = 0:n:n; field_z = 0:n:n; stem3(field_x,field_y,field_z,'--.y'); hold on; i=11; %要创建n个面积为1的障碍建筑物% x,y,z想要改成随机可将数组成员改成rand*20x=1:1:i; x=[2 4 3 5 7 10 13 14 16 9 8]; %创建建筑的x轴坐标分别为x-x+1;y=1:1:i; y=[4 17 14 3 11 13 8 16 6 8 18];%创建建筑的y轴坐标分别为y-y+1;z=1:1:i; z=[5 7 7 12 6 11 4 18 3 15 6];%创建建筑的高度分别为z; for a=1:i % 创建第a个面积为1的建筑,将[x(a),y(a)]右上角的方块设为障碍物 x1=x(a):0.01:x(a)+1; y1=y(a)+0.99:0.0001:y(a)+1; z1=z(a)-0.01:0.0001:z(a); stem3(x1,y1,z1,'.k'); x2=x(a)+0.99:0.0001:x(a)+1; y2=y(a):0.01:y(a)+1; z2=z(a)-0.01:0.0001:z(a); stem3(x2,y2,z2,'.k'); x3=x(a):0.0001:x(a)+0.01; y3=y(a):0.01:y(a)+1; z3=z(a)-0.01:0.0001:z(a); stem3(x3,y3,z3,'.k'); x4=x(a):0.01:x(a)+1; y4=y(a):0.0001:y(a)+0.01; z4=z(a)-0.01:0.0001:z(a); stem3(x4,y4,z4,'.k'); for c=1:z(a) field(x(a)+1,y(a)+1,c)=inf; endendj=9; %要创建n个面积为1的障碍建筑物x=1:1:j; x=[14 17 11 3 6 10 17 7 0]; %创建建筑的x轴坐标分别为x-x+2;y=1:1:j; y=[8 11 2 6 4 16 7 12 1];%创建建筑的y轴坐标分别为y-y+2;z=1:1:j; z=[2 9 13 11 4 18 5 7 6];%创建建筑的高度分别为z; for b=1:j % 创建第m个面积为4的建筑 x1=x(b):0.01:x(b)+2; y1=y(b)+2:0.0001:y(b)+2.02; z1=z(b)-0.02:0.0001:z(b); stem3(x1,y1,z1,'.b'); x2=x(b):0.0001:x(b)+0.02; y2=y(b):0.01:y(b)+2; z2=z(b)-0.02:0.0001:z(b); stem3(x2,y2,z2,'.b'); x3=x(b)+2:0.0001:x(b)+2.02; y3=y(b):0.01:y(b)+2; z3=z(b)-0.02:0.0001:z(b); stem3(x3,y3,z3,'.b'); x4=x(b):0.01:x(b)+2; y4=y(b):0.0001:y(b)+0.02; z4=z(b)-0.02:0.0001:z(b); stem3(x4,y4,z4,'.b'); for d=1:z(b) field(x(b)+1,y(b)+1,d)=inf; field(x(b)+2,y(b)+1,d)=inf; field(x(b)+1,y(b)+2,d)=inf; field(x(b)+2,y(b)+2,d)=inf; endend % field(ind2sub([n n n],ceil(n^3.*rand(n*n*n*wallpercent,1)))) = Inf;%向上取整以上就是作图并存储到数组部分的代码了,如果想改变障碍物的位置、数量、颜色等,只需要修改对应变量值就可以实现。但由于,我只编写了面积为1以及面积为4的两种障碍物,如果你想要创建别的形状或形式的障碍物,可以参考上述创建的方式自己改进一下。
(这里没有采取函数的形式,需要插入后续代码的前部分。)
2、随机生成起点及终点
这部分其实还是博主慕羽★的思想,指路 ↓↓↓详细介绍用MATLAB实现基于A*算法的路径规划(附完整的代码,代码逐行进行解释)(一)--------A*算法简介和环境的创建_a*算法路径规划matlab_慕羽★的博客-CSDN博客
只针对维数拓展做了些许改进,确保代码正常运行,部分如下:
%% 随机生成起始点startposind和终止点goalposind,生成元胞数组costchart和fieldpointersif Environment_reset startposind = sub2ind([n,n,n],[ceil(n.*rand),ceil(n.*rand),ceil(n.*rand)]); %随机生成起始点的索引值,n在【1,20】 while field(startposind(1),startposind(2),startposind(3))==inf startposind = sub2ind([n,n,n],[ceil(n.*rand),ceil(n.*rand),ceil(n.*rand)]); %随机生成起始点 if field(startposind(1),startposind(2),startposind(3))==1 break; end end plot3(startposind(1)-0.5,startposind(2)-0.5,startposind(3)-0.5,'g.','markersize',20); startposind = sub2ind([n,n,n],startposind(1),startposind(2),startposind(3)); goalposind = sub2ind([n,n,n],[ceil(n.*rand),ceil(n.*rand),ceil(n.*rand)]); %随机生成终止点的索引值 while field(goalposind(1),goalposind(2),goalposind(3))==inf goalposind = sub2ind([n,n,n],[ceil(n.*rand),ceil(n.*rand),ceil(n.*rand)]); %随机生成起始点 if field(goalposind(1),goalposind(2),goalposind(3))==1 break; end end plot3(goalposind(1)-0.5,goalposind(2)-0.5,goalposind(3)-0.5,'y.','markersize',20); goalposind = sub2ind([n,n,n],goalposind(1),goalposind(2),goalposind(3)); 二、三维算法的实现
1、首先是路径规划的主代码,就直接给可向26方向拓展的代码了。
%% 开始进行路径规划% 路径规划中用到的一些矩阵的初始化setOpen = [startposind]; setOpenCosts = [0]; setOpenHeuristics = [Inf];setClosed = []; setClosedCosts = [];movementdirections = {'R','L','B','F','D','U','DB','DF','UB','UF','RB','RF','LB','LF','DR','DL','UR','UL'}; %父节点移动方向右、左、后、前、下、上,下后、下前、上后、上前,右后、右前、左后、左前,下右、下左、上右、上左tic% 这个while循环是本程序的核心,利用循环进行迭代来寻找终止点while ~max(ismember(setOpen,goalposind)) && ~isempty(setOpen) [temp, ii] = min(setOpenCosts + setOpenHeuristics); %寻找拓展出来的最小值 %这个函数的作用就是把输入的点作为父节点,然后进行拓展找到子节点,并且找到子节点的代价,并且把子节点距离终点的代价找到 [costs,heuristics,posinds] = findFValue(Corner_obstacles,n,setOpen(ii),setOpenCosts(ii), field,goalposind); setClosed = [setClosed; setOpen(ii)]; % 将找出来的拓展出来的点中代价最小的那个点串到矩阵setClosed 中 setClosedCosts = [setClosedCosts; setOpenCosts(ii)]; % 将拓展出来的点中代价最小的那个点的代价串到矩阵setClosedCosts 中 % 从setOpen中删除刚才放到矩阵setClosed中的那个点 %如果这个点位于矩阵的内部 if (ii > 1 && ii < length(setOpen)) setOpen = [setOpen(1:ii-1); setOpen(ii+1:end)]; setOpenCosts = [setOpenCosts(1:ii-1); setOpenCosts(ii+1:end)]; setOpenHeuristics = [setOpenHeuristics(1:ii-1); setOpenHeuristics(ii+1:end)]; %如果这个点位于矩阵第一行 elseif (ii == 1) setOpen = setOpen(2:end); setOpenCosts = setOpenCosts(2:end); setOpenHeuristics = setOpenHeuristics(2:end); %如果这个点位于矩阵的最后一行 else setOpen = setOpen(1:end-1); setOpenCosts = setOpenCosts(1:end-1); setOpenHeuristics = setOpenHeuristics(1:end-1); end % 把拓展出来的点中符合要求的点放到setOpen 矩阵中,作为待选点 for jj=1:length(posinds) if ~isinf(costs(jj)) % 判断该点(方格)处没有障碍物 % 判断一下该点是否 已经存在于setOpen 矩阵或者setClosed 矩阵中 % 如果我们要处理的拓展点既不在setOpen 矩阵,也不在setClosed 矩阵中 if ~max([setClosed; setOpen] == posinds(jj)) fieldpointers(posinds(jj)) = movementdirections(jj); costchart(posinds(jj)) = costs(jj); setOpen = [setOpen; posinds(jj)]; setOpenCosts = [setOpenCosts; costs(jj)]; setOpenHeuristics = [setOpenHeuristics; heuristics(jj)]; % 如果我们要处理的拓展点已经在setOpen 矩阵中 elseif max(setOpen == posinds(jj)) I = find(setOpen == posinds(jj)); % 如果通过目前的方法找到的这个点,比之前的方法好(代价小)就更新这个点 if setOpenCosts(I) > costs(jj) costchart(setOpen(I)) = costs(jj); setOpenCosts(I) = costs(jj); setOpenHeuristics(I) = heuristics(jj); fieldpointers(setOpen(I)) = movementdirections(jj); end % 如果我们要处理的拓展点已经在setClosed 矩阵中 else I = find(setClosed == posinds(jj)); % 如果通过目前的方法找到的这个点,比之前的方法好(代价小)就更新这个点 if setClosedCosts(I) > costs(jj) costchart(setClosed(I)) = costs(jj); setClosedCosts(I) = costs(jj); fieldpointers(setClosed(I)) = movementdirections(jj); end end end end if isempty(setOpen) break; end% set(axishandle,'CData',[costchart costchart(:,end); costchart(end,:) costchart(end,end)]);% set(gca,'CLim',[0 1.1*max(costchart(find(costchart < Inf)))]); drawnow; endtoc2、三维的路径回溯findwayback函数:
%% 用于路径回溯的findWayBack函数%findWayBack函数用来进行路径回溯,这个函数的输入参数是终止点goalposind和矩阵fieldpointers,输出参数是Pfunction p = findWayBack(n,goalposind,fieldpointers) posind = goalposind; [px,py,pz] = ind2sub([n,n n],posind); % 将索引值posind转换为坐标值 [px,py,pz] p = [px py pz]; %利用while循环进行回溯,当我们回溯到起始点的时候停止,也就是在矩阵fieldpointers中找到S时停止 while ~strcmp(fieldpointers{posind},'S') switch fieldpointers{posind} case 'L' % ’L’ 表示当前的点是由左边的点拓展出来的 px = px - 1; case 'R' % ’R’ 表示当前的点是由右边的点拓展出来的 px = px + 1; case 'U' % ’U’ 表示当前的点是由上面的点拓展出来的 pz = pz + 1; case 'D' % ’D’ 表示当前的点是由下边的点拓展出来的 pz = pz - 1; case 'B' % ’B’ 表示当前的点是由后面的点拓展出来的 py = py - 1; case 'F' % ’F’ 表示当前的点是由前面的点拓展出来的 py = py + 1; case 'DB' % ’DB’ 表示当前的点是由下后的点拓展出来的 py = py - 1; pz = pz - 1; case 'DF' % ’DF’ 表示当前的点是由下前的点拓展出来的 py = py + 1; pz = pz - 1; case 'UB' % ’UB’ 表示当前的点是由上后的点拓展出来的 py = py - 1; pz = pz + 1; case 'UF' % ’UF’ 表示当前的点是由上前的点拓展出来的 py = py + 1; pz = pz + 1; case 'RB' % ’RB’ 表示当前的点是由右后的点拓展出来的 px = px + 1; py = py - 1; case 'RF' % ’RF’ 表示当前的点是由右前的点拓展出来的 px = px + 1; py = py + 1; case 'LB' % ’LB’ 表示当前的点是由左后的点拓展出来的 px = px - 1; py = py - 1; case 'LF' % ’RF’ 表示当前的点是由右前的点拓展出来的 px = px - 1; py = py + 1; case 'DR' % ’DR’ 表示当前的点是由下右的点拓展出来的 px = px + 1; pz = pz - 1; case 'DL' % ’DL’ 表示当前的点是由下左的点拓展出来的 px = px - 1; pz = pz - 1; case 'UR' % ’UR’ 表示当前的点是由上右的点拓展出来的 px = px + 1; pz = pz + 1; case 'UL' % ’UL’ 表示当前的点是由上左的点拓展出来的 px = px - 1; pz = pz + 1; end p = [p; px py pz]; posind = sub2ind([n n n],px,py,pz);% 将坐标值转换为索引值 endend3、主函数调用到的算法部分,findvalue函数:
%% 用于拓展的findFValue函数,由一个父节点拓展多个子节点,分别计算出costs和heuristic%这个函数的作用就是把输入的点作为父节点,然后进行拓展找到子节点,并且找到子节点的代价,并且把子节点距离终点的代价找到。%函数的输出量中costs表示拓展的子节点到起始点的代价,heuristics表示拓展出来的点到终止点的距离大约是多少,posinds表示拓展出来的子节点%拓展方向分别为左、右、前、后、上、下, 上前、上后、下前,下后, 左前、左后、右前、右后, 上左、上右、下左、下右function [cost,heuristic,posinds] = findFValue(Corner_obstacles,n,posind,costsofar,field,goalind) [currentpos(1) currentpos(2) currentpos(3)] = ind2sub([n n n],posind); %将要进行拓展的点(也就是父节点)的索引值拓展成坐标值 [goalpos(1) goalpos(2) goalpos(3)] = ind2sub([n n n],goalind); %将终止点的索引值拓展成坐标值 cost = Inf*ones(18,1); heuristic = Inf*ones(18,1); pos = ones(18,3); %将矩阵cost和heuristic初始化为4x1的无穷大值的矩阵,pos初始化为4x2的值为1的矩阵 % 拓展方向一,左 newx = currentpos(1) - 1; newy = currentpos(2); newz = currentpos(3); if newx > 0 pos(1,:) = [newx newy newz];% heuristic(1) = abs(goalpos(1)-newx) + abs(goalpos(2)-newy) + abs(goalpos(3)-newz); % 曼哈顿距离公式 heuristic(1) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(1) = costsofar + field(newx,newy,newz); end % 拓展方向二,右 newx = currentpos(1) + 1; newy = currentpos(2); newz = currentpos(3); if newx <= n pos(2,:) = [newx newy newz];% heuristic(2) = abs(goalpos(1)-newx) + abs(goalpos(2)-newy) + abs(goalpos(3)-newz); % 曼哈顿距离公式 heuristic(2) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(2) = costsofar + field(newx,newy,newz); end % 拓展方向三,前 newx = currentpos(1); newy = currentpos(2)+1; newz = currentpos(3); %向前拓展,地图上y+1,数组中y if newy <= n pos(3,:) = [newx newy newz];% heuristic(3) = abs(goalpos(1)-newx) + abs(goalpos(2)-newy) + abs(goalpos(3)-newz); % 曼哈顿距离公式 heuristic(3) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(3) = costsofar + field(newx,newy,newz); end % 拓展方向四,后 newx = currentpos(1); newy = currentpos(2)-1; newz = currentpos(3); if newy > 0 pos(4,:) = [newx newy newz];% heuristic(4) = abs(goalpos(1)-newx) + abs(goalpos(2)-newy) + abs(goalpos(3)-newz); % 曼哈顿距离公式 heuristic(4) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(4) = costsofar + field(newx,newy,newz); end % 拓展方向五,上 newx = currentpos(1); newy = currentpos(2); newz = currentpos(3)+1; if newz <= n pos(5,:) = [newx newy newz];% heuristic(5) = abs(goalpos(1)-newx) + abs(goalpos(2)-newy) + abs(goalpos(3)-newz); % 曼哈顿距离公式 heuristic(5) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(5) = costsofar + field(newx,newy,newz); end % 拓展方向六,下 newx = currentpos(1); newy = currentpos(2); newz = currentpos(3)-1; if newz > 0 pos(6,:) = [newx newy newz];% heuristic(6) = abs(goalpos(1)-newx) + abs(goalpos(2)-newy) + abs(goalpos(3)-newz); % 曼哈顿距离公式 heuristic(6) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(6) = costsofar + field(newx,newy,newz); end % 拓展方向七,上前 newx = currentpos(1); newy = currentpos(2)+1; newz = currentpos(3)+1; if (newy <= n)&&(newz <= n) pos(7,:) = [newx newy newz]; heuristic(7) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(7) = costsofar + sqrt(2)*field(newx,newy,newz); if Corner_obstacles cost(7) = cost(7) + field(newx,newy,newz-1)-1; %代价为根号2的拓展节点,添加不可穿越四角障碍的规则,向上前方拓展时,判断新拓展点下方是否有障碍 end end % 拓展方向八,上后 newx = currentpos(1); newy = currentpos(2)-1; newz = currentpos(3)+1; if (newy > 0)&&(newz <= n) pos(8,:) = [newx newy newz]; heuristic(8) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(8) = costsofar + sqrt(2)*field(newx,newy,newz); if Corner_obstacles cost(8) = cost(8)+ field(newx,newy,newz-1)-1; %向上后方拓展时,判断新拓展点下方是否有障碍 end end % 拓展方向九,下前 newx = currentpos(1); newy = currentpos(2)+1; newz = currentpos(3)-1; if (newy <= n)&&(newz > 0) pos(9,:) = [newx newy newz]; heuristic(9) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(9) = costsofar + sqrt(2)*field(newx,newy,newz); if Corner_obstacles cost(9) = cost(9)+ field(newx,newy-1,newz)-1; %向下前方拓展时,判断新拓展点后方是否有障碍 end end % 拓展方向十,下后 newx = currentpos(1); newy = currentpos(2)-1; newz = currentpos(3)-1; if (newy > 0)&&(newz > 0) pos(10,:) = [newx newy newz]; heuristic(10) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(10) = costsofar + sqrt(2)*field(newx,newy,newz); if Corner_obstacles cost(10) = cost(10)+ field(newx,newy+1,newz)-1; %向下后方拓展时,判断新拓展点前方是否有障碍 end end % 拓展方向十一,左前 newx = currentpos(1)-1; newy = currentpos(2)+1; newz = currentpos(3); if (newx > 0)&&(newy <= n) pos(11,:) = [newx newy newz]; heuristic(11) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(11) = costsofar + sqrt(2)*field(newx,newy,newz); if Corner_obstacles cost(11) = cost(11)+ field(newx+1,newy,newz)+field(newx,newy-1,newz)-2; %向左前方拓展时,判断新拓展点右方及后方是否有障碍 end end % 拓展方向十二,左后 newx = currentpos(1)-1; newy = currentpos(2)-1; newz = currentpos(3); if (newx > 0)&&(newy > 0) pos(12,:) = [newx newy newz]; heuristic(12) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(12) = costsofar + sqrt(2)*field(newx,newy,newz); if Corner_obstacles cost(12) = cost(12)+ field(newx+1,newy,newz)+field(newx,newy+1,newz)-2; %向左后方拓展时,判断新拓展点右方及前方是否有障碍 end end % 拓展方向十三,右前 newx = currentpos(1)+1; newy = currentpos(2)+1; newz = currentpos(3); if (newx <= n)&&(newy <= n) pos(13,:) = [newx newy newz]; heuristic(13) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(13) = costsofar + sqrt(2)*field(newx,newy,newz); if Corner_obstacles cost(13) = cost(13)+field(newx-1,newy,newz)+field(newx,newy-1,newz)-2; %向右前方拓展时,判断新拓展点左方及后方是否有障碍 end end % 拓展方向十四,右后 newx = currentpos(1)+1; newy = currentpos(2)-1; newz = currentpos(3); if (newx <= n)&&(newy > 0) pos(14,:) = [newx newy newz]; heuristic(14) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(14) = costsofar + sqrt(2)*field(newx,newy,newz); if Corner_obstacles cost(14) = cost(14)+ field(newx-1,newy,newz)+field(newx,newy+1,newz)-2; %向右后方拓展时,判断新拓展点左方及前方是否有障碍 end end % 拓展方向十五,上左 newx = currentpos(1)-1; newy = currentpos(2); newz = currentpos(3)+1; if (newx > 0)&&(newz <= n) pos(15,:) = [newx newy newz]; heuristic(15) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(15) = costsofar + sqrt(2)*field(newx,newy,newz); if Corner_obstacles cost(15) = cost(15)+ field(newx,newy,newz-1)-1; %向上左方拓展时,判断新拓展点下方是否有障碍 end end % 拓展方向十六,上右 newx = currentpos(1)+1; newy = currentpos(2); newz = currentpos(3)+1; if (newx <= n)&&(newz <= n) pos(16,:) = [newx newy newz]; heuristic(16) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(16) = costsofar + sqrt(2)*field(newx,newy,newz); if Corner_obstacles cost(16) = cost(16)+ field(newx,newy,newz-1)-1; %向上右方拓展时,判断新拓展点下方是否有障碍 end end % 拓展方向十七,下左 newx = currentpos(1)-1; newy = currentpos(2); newz = currentpos(3)-1; if (newx > 0)&&(newz > 0) pos(17,:) = [newx newy newz]; heuristic(17) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(17) = costsofar + sqrt(2)*field(newx,newy,newz); if Corner_obstacles cost(17) = cost(17)+field(newx+1,newy,newz)-1; %向下左方拓展时,判断新拓展点右方是否有障碍 end end % 拓展方向十八,下右 newx = currentpos(1)+1; newy = currentpos(2); newz = currentpos(3)-1; if (newx <= n)&&(newz > 0) pos(18,:) = [newx newy newz]; heuristic(18) = sqrt((goalpos(1)-newx)^2 +(goalpos(2)-newy)^2+(goalpos(3)-newz)^2); %欧几里得距离 cost(18) = costsofar + sqrt(2)*field(newx,newy,newz); if Corner_obstacles cost(18) = cost(18)+ field(newx-1,newy,newz)-1; %向下右方拓展时,判断新拓展点左方是否有障碍 end end posinds = sub2ind([n n n],pos(:,1),pos(:,2),pos(:,3)); % 将拓展出来的所以子节点的坐标值转换为索引值,储存在数组posinds里end4、到这里,就可以实现使用A*算法进行路径规划了,贴上一张运行结果图
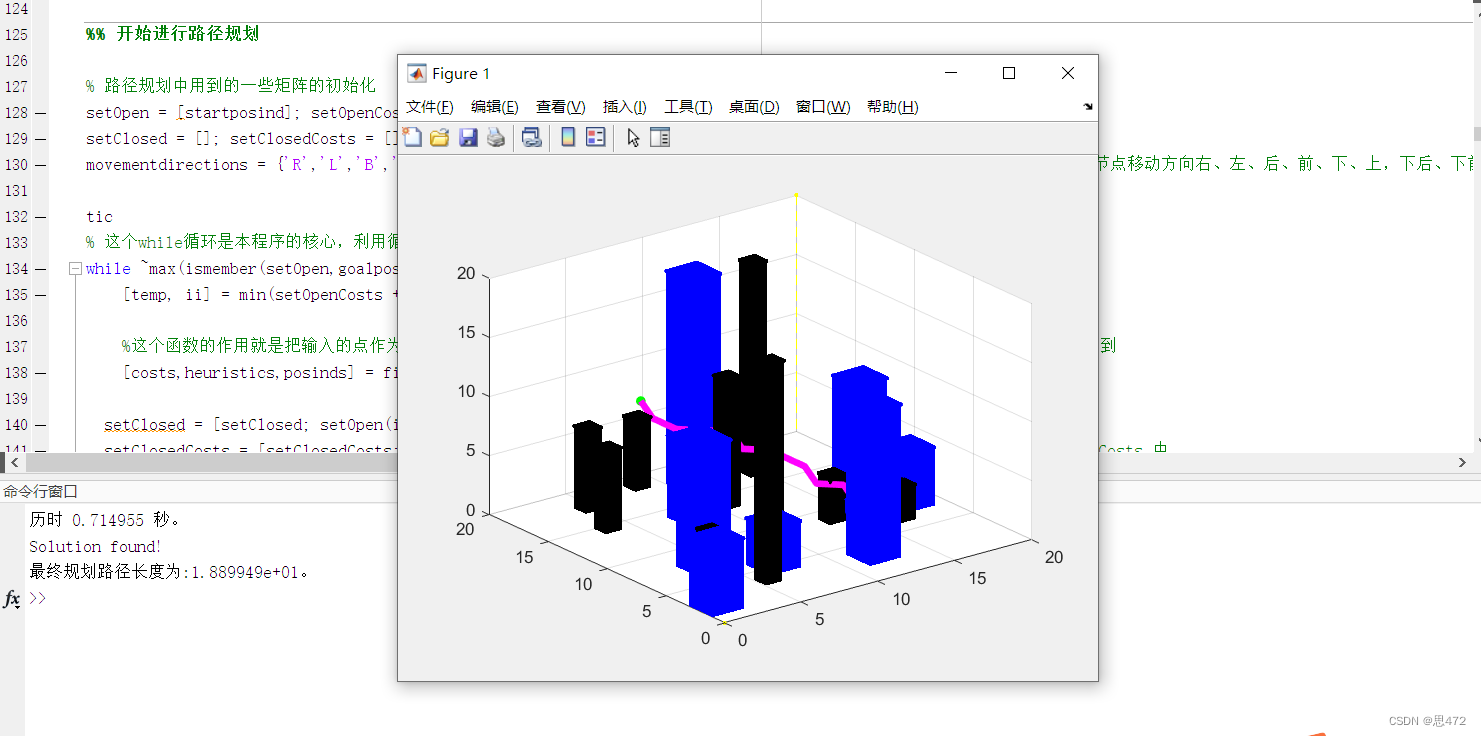
三、基于背景的三维算法的改进
1、增加普通转弯代价参数Normal_turns,以减少物流无人机在作业时的转弯次数,在对角模式下才能更好体现
2、添加有关参数判断公式,在没到达边界重量之前,weights = boundary * M(max)/M(实际);到达边界值之后,weights=1.
3、增加转弯计数参数turn_count,用来存放拐弯次数
4、增加路长计算参数Road_Long,用来计算规划路径长度
5、增设建筑物危险系数代价proximity_cost,另建筑物附近代价大于相隔较远处代价
以上就是我改进的地方,增设的一些参数,将其放到合适的位置实现想要的效果。如参数Normal_turns,在函数findFValue中添加,注意在调用时也要添加,否则会报错,如下所示:
[costs,heuristics,posinds] = findFValue(fieldpointers,Normal_turns,Corner_obstacles,n,setOpen(ii),setOpenCosts(ii), field,goalposind);在findFValue函数的每次转弯中进行判断,只要不是直线行驶,即判断为转弯,令转弯次数加一,以下列代码为例:
if ~strcmp(fieldpointers{posind},'R') % 不是直线行驶,需加上拐弯代价 cost(1)= cost(1) + Normal_turns; end参数proximity_cost是通过改变环境数组实现的,将储存建筑物等数据的三维数组中,所有存储inf的栅格附近的栅格都增加系数proximity_cost,代表无人机靠近建筑物需要承担适量风险,得到的路径也将适当远离障碍物。当然,可能会使耗能增加,因此靠近建筑物的风险和无人机耗能之间的平衡关系,就由你自己决定了,可按自己的思路发挥~
上述改进思路仅供参考,我也是从各论文里学习到的,融合我自己的想法实现,再次感谢为我提供帮助的人们(不一一例举啦),让我顺利的完成本项目。提供的代码不完全,只提供一些思路而已,还是建议自己学习一下吧,有误之处,欢迎指出~