
文章目录
?前言?C++中的随机函数✈️介绍✈️使用✈️用C++的暴力求解✈️用C++的优化解法 ?Java中的Math.random()函数
?前言
大家好啊!阿辉在刷题时遇到一个很有意思的题LeetCode470.用rand7()实现rand10(),这道题我花了两个多小时研究?,好吧,别说我菜,阿辉也是收获到了一些东西,这里分享给大家!!!
题目描述:
rand7 可生成[1,7]范围内的均匀随机整数,试写一个方法rand10生成[1,10]范围内的均匀随机整数。你只能调用rand7()且不能调用其他方法。请不要使用系统的Math.random()方法。 ?C++中的随机函数
✈️介绍
C语言中的rand()和srand()这俩阿辉就不说了,相信大家都会。
阿辉在这里给大家介绍关于随机数生成的三个类,random_device、mt19937以及uniform_int_distribution,这三个类的声明都包含在<random>头文件中。
random_device:它提供了一种生成真正随机数的方法。它通常用于为伪随机数生成器提供种子值mt19937:mt19937是C++标准库中提供的一个伪随机数生成器引擎。它基于梅森旋转算法(Mersenne Twister)实现,可以生成高质量的伪随机数序列
使用mt19937引擎可以生成均匀分布的整数和实数随机数。通常情况下,我们可以通过random_device来初始化mt19937引擎,以产生更加随机的数值序列uniform_int_distribution:用于生成均匀分布的整数随机数。uniform_int_distribution类提供了一种方法,可以在指定的整数范围内生成均匀分布的随机数。通过将该类与随机数引擎(如mt19937)结合使用,可以生成符合特定范围要求的随机整数
uniform_int_distribution设置的范围是全闭的即包括上下界,比如范围[1,7],包括1和7
✈️使用
它们如何使用呢?我们接着看:
我们来用上面介绍的三个类,来写出题目中提供的rand7()函数,均匀生成[1,7]的随机整数,上代码:
int rand7() {random_device rd;//设置随机数种子mt19937 gen(rd());//用随机数种子初始化随机数引擎uniform_int_distribution<int> dis(1, 7);//设置随机数范围,等概率返回[1,7]的整数包括1和7return dis(gen);//等概率拿到1~7的数字}✈️用C++的暴力求解
关于这道题的解法,怎么得到rand10()函数等概率得到[1,10]呢?这阿辉先讲一个简单且普适的方法,任何此类型题都可以套用
题目要求只能用rand7()改造出rand10()
首先我们可以用rand7()改出一个等概率返回0和1的01发生器,怎么改,阿辉先写代码再解释:
int rand01() {//将上述rand7()改造成0,1发生器while(true){int num = rand7();//我们知道rand7()函数等概率返回1~7if(num != 7)//num等于7的时候让num重新生成return num < 4 ? 0 : 1;//1、2、3返回0;4、5、6返回1;0和1等概率返回}}解释:我们知道rand7()函数等概率返回1 ~ 7的整数,我们只取起生成的1 ~ 6的数字,对于数字7我们则重新生成,然后对于num的值只会取到1 ~ 6,然后我们只需要将1~6的数字等分成两组,然后只要取到1,2,3我们就返回0,取到4,5,6我们就返回1,这样得到1和0就是等概率的了
上述这种不取数字7的方式被称作拒绝取样
可能铁子们会说,咱们搞这个01发生器rand01()用什么用,阿辉告诉你这用处可就大了,有了01发生器rand01()我们可以得到任意范围的均匀随机整数
各位注意骚操作来了:
比如本题的rand10()要求等概率返回[1,10],对于10,我们要表示10需要4个二进制位,所以我们只需要调4次01发生器即可得到rand10(),为什么?上图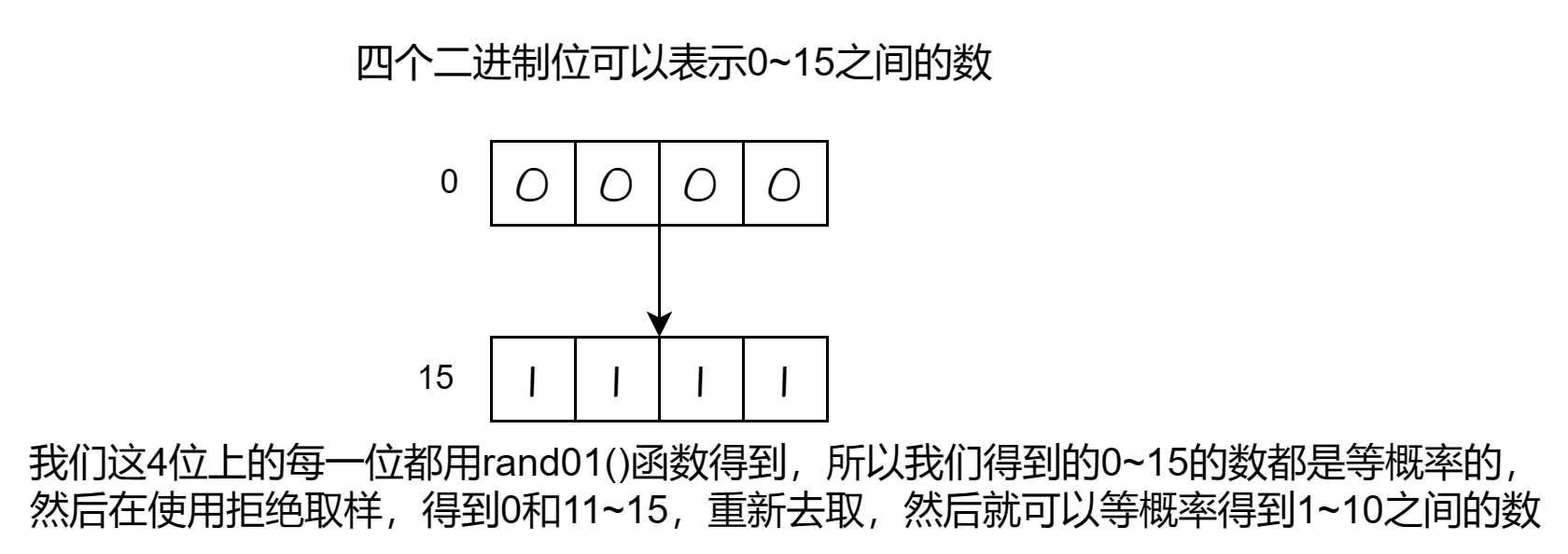
1~15这16个数的二进制形式都唯一的,每一位不管是0 还是1 概率都是0.5,所以得到1~15之间每一个数的概率都是1/16(总不能叫阿辉讲二项分布吧?♀️)完整代码如下:
int rand7() {random_device rd;//设置随机数种子mt19937 gen(rd());//随机数引擎uniform_int_distribution<int> dis(1, 7);//等概率返回[1,7]的整数包括1和7return dis(gen);//等概率拿到1~7的数字}int rand01() {//将上述rand7()改造成0,1发生器while(true){int num = rand7();//我们知道rand7()函数等概率返回1~7if(num != 7)//num等于7的时候让num重新生成return num < 4 ? 0 : 1;//1、2、3返回0;4、5、6返回1;0和1等概率返回}}int rand10() {while(true) {//下面每一个rand01()都表示一个二进制位,用右移操作符移到正确的位置int num = (rand01() << 3) + (rand01() << 2) + (rand01() << 1) + rand01();if(num != 0 && num <11)//得到0和11~15重新去取return num;} }阿辉还写了一个验证测试,用rand10()循环生成10万次,看看各个数的出现概率是否一致
int main() {int TestTimes = 100000;int* count = new int[10]();for (int i = 0; i < TestTimes; i++) {for (int j = 1; j <= 10; j++) {if (rand10() == j)count[j - 1]++;}}for (int i = 1; i <= 10; i++) {cout << "数字" << i << "出现的概率是" << (double)count[i - 1] / (double)TestTimes << endl;}delete[] count;return 0;}
实际测出,每一个数字出现的概率都大致是0.1
在LeetCode上面运行描述如下:
✈️用C++的优化解法
上面的暴力解法说实话效率不是很高,一开始阿辉测的是100万次,结果一直不出结果,我还以为代码写错了,程序死循环了,其实是效率太低了。
为什呢?01发生器rand01()有1/7的概率重新调rand7(),rand01()改成rand10(),在rand10()中要调用4次rand01(),每调用一次rand10()又有6/16的概率重新调4次rand01(),这样又会使rand7()重复调用,rand7()被调用的次数太多效率自然就低了
我们的优化的方向就是减少rand7()的调用,其实对于一个rand7()函数我们可以把它看做一个7进制生成器,因为rand7() - 1会等概率的得到0 ~ 6的数字,而rand7() - 1相当于权重为70的位,而(rand7() - 1) × 7k就表示权重为7k的位,这时我们只需要两个7进制位即可表示[0,48],所以调用两次rand7()函数即可等概率的返回[0,48]之间的数字(原理与上述暴力解法中二进制一样)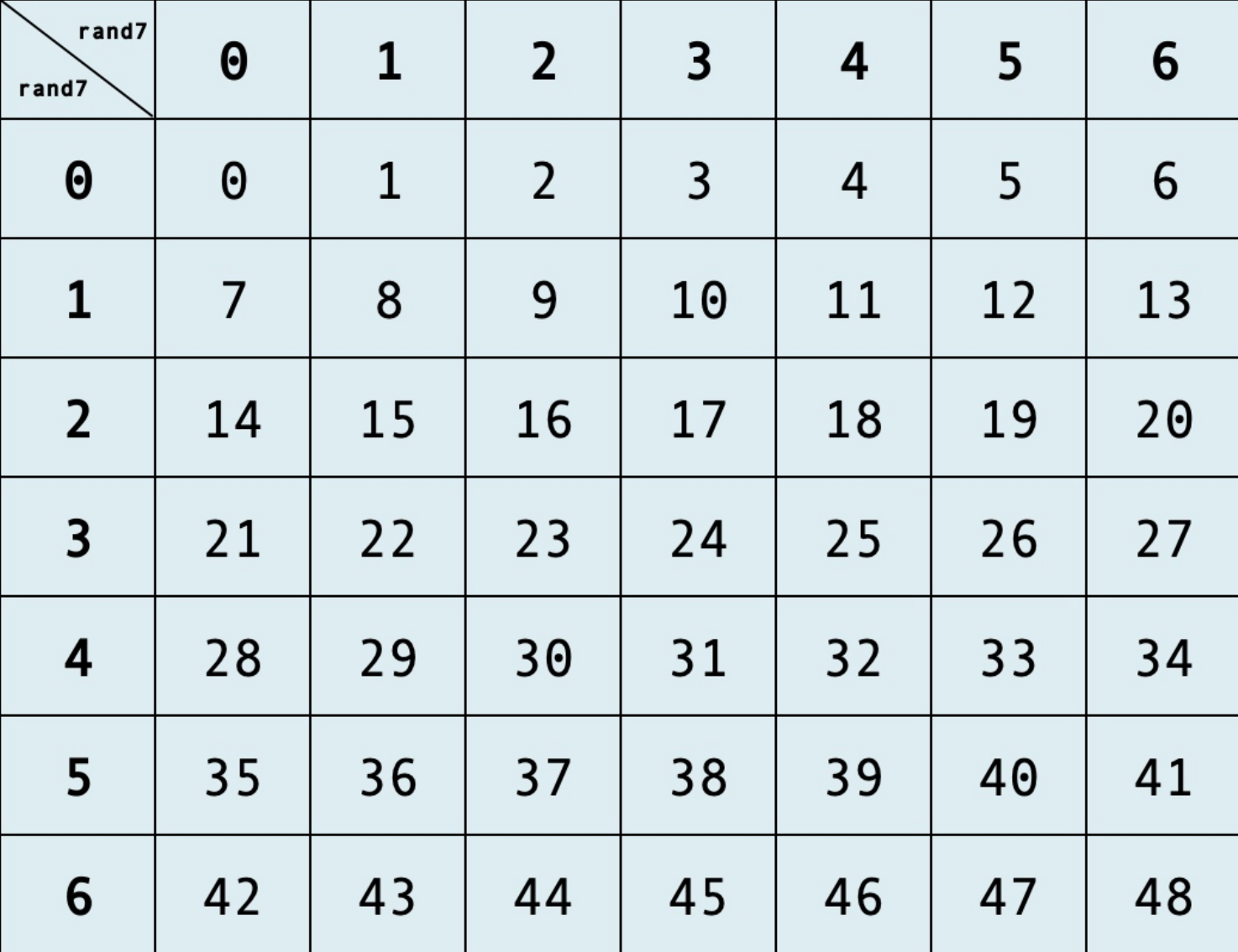
不过在[0,48]这些数字中我们只能用到[0,9]、[10,19]、[20,29]以及[30,39]这些数字,因为这些数字模上10会得到0 ~ 9,而且是等概率得到。为什么[40,48]这些数字不行,因为缺了49,加上它们会导致得到9比得到0 ~ 8的概率低,也就不是等概率了,这里我们仅有9/48的概率重复调用
代码如下:
int rand7() {random_device rd;//设置随机数种子mt19937 gen(rd());//随机数引擎uniform_int_distribution<int> dis(1, 7);//等概率返回[1,7]的整数包括1和7return dis(gen);//等概率拿到1~7的数字}int rand10() { while (true) { int num = (rand7() - 1) * 7 + (rand7() - 1); if (num >= 1 && num <= 40) return x % 10 + 1; }}上述代码在LeetCode运行描述如下:
其实还可以继续优化上面的代码我们浪费了[40,48]的数字,我们如何利用他们呢,你想只要我们得到了[40,48]的数字,说明我们还得在重复生成一次num,这一次生成的num在[40,48]的概率为仍为9/48这时又会重新生成num,我们只要让这个概率下降即可优化
如何优化:
当num得到[40,48]的数字时,把num % 40,即可等概率得到0 ~ 8的数字,这时我们就得到了9进制的生成器,然后(num % 40) * 7 + rand7()就可以等概率得到[1,63]范围的数字,这些数字又可以模上10等概率得到0 ~ 9,仅有61,62,63三个数字不能用,这一次重新生成num的概率就更低了
代码如下:
int rand10() { while (true) { int x = (rand7() - 1) * 7 + (rand7() - 1); // 0~48 if (x >= 1 && x <= 40) return x % 10 + 1; x = (x % 40) * 7 + rand7(); // 1~63 if (x <= 60) return x % 10 + 1;}这一次直接击败LeetCode%99的人
至于剩下的61,62,63这三个数字还能不能优化呢?实际上是可以的,但是阿辉算过了,继续优化,下一次重复的概率仍然是1 / 21,大家下去可以尝试优化一下,阿辉在这就不展开了,方法就和优化[40,48]这9个数一样
?Java中的Math.random()函数
在Java中有这么一个函数Math.random()用来生成随机数,它与C++中不同,这个函数会等概率随机返回[0,1)的小数(包括0,不包括1),数学上不可能做到因为 0 ~ 1之间的小数有无穷多个,但是计算机可以,因为计算机小数有精度也就是有有限个小数
用Java写rand7()函数
public static int rand7(){ //Math.random()*7即可得到[0,7)之间的全体实数不包括7,我们给它强转成int //就会等概率得到0~6这7个整数,然后加1就能等概率得到1~7 return (int)(Math.random() * 7) + 1; }用Java写rand7()改rand10()
public class LeetCode470 { public static int rand7(){ return (int)(Math.random() * 7) + 1; } public static int rand10(){ while (true){ int num = (rand7() - 1) * 7 + rand7() - 1; if(num < 40) return num % 10 + 1; num = (num % 40) * rand7(); if(num < 61) return num % 10 + 1; } }在LeetCode的运行描述:
