【排序算法】—— 希尔排序
目录
一、希尔排序原理1. 插入排序的问题2. 希尔排序的思路 二、希尔排序的相关问题1. 为什么插入排序那么多但效率却很高2. 如何选择希尔增量 三、代码实现1. 代码实现思路2. 实现代码
希尔排序是对直接插入排序的优化,在学习之前,没有学过插入排序的童鞋们建议先学习插入排序:点击跳转到插入排序?
一、希尔排序原理
1. 插入排序的问题
逆序有序的数组排序时,时间复杂度为 O ( n 2 ) O(n^2) O(n2),此时效率最低
顺序有序的数组排序时,时间复杂度为 O ( n ) O(n) O(n),此时效率最高
我们发现,当被排序的对象越接近有序时,插入排序的效率越高,那我们是否有办法将数组变成接近有序后再用插入排序,此时希尔大佬就发现了这个排序算法,并命名为希尔排序
2. 希尔排序的思路
希尔排序是对插入排序的优化,基本思路是先选定一个整数作为增量,把待排序文件中的所有数据分组,以每个距离的等差数列为一组,对每一组进行排序,然后将增量缩小,继续分组排序,重复上述动作,直到增量缩小为1时,排序完正好有序。
希尔排序原理是每一对分组进行排序后,整个数据就会更接近有序,当增量缩小为1时,就是插入排序,但是现在的数组非常接近有序,移动的数据很少,所以效率非常高,所以希尔排序又叫缩小增量排序。
每次排序让数组接近有序的过程叫做预排序,最后一次插入是直接插入排序
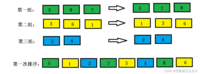
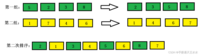
以3作为增量对数组进行分组,以下数组被分成3组,每组之间都是以3的等差数列


二、希尔排序的相关问题
1. 为什么插入排序那么多但效率却很高
希尔排序中待排数据每次是以增量的移动步数空出插入位置,所以效率比普通插入一次一步的移动方式要快

每一次排序之后数组就会变得接近有序,插入排序的移动次数就会越来越少,效率也不是普通的插入排序能比的了
希尔排序移动次数:共移动8步
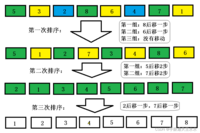

综上所述:希尔排序在越大的数组上更能发挥优势,因为步子迈的更大,减少插入排序的移动次数更多
2. 如何选择希尔增量
希尔排序的分析是一个复杂的问题,它的时间是一个关于增量序列的函数,这涉及到一些数学上未能攻克的难题,所以目前为止对于希尔增量到底怎么取也没有一个最优的值,但是经过大量研究已经有一些局部的结论,在这里并不展开叙述。
最初希尔提出的增量是 gap = n / 2,每一次排序完让增量减少一半gap = gap / 2,直到gap = 1时排序变成了直接插入排序。直到后来Knuth提出的gap = [gap / 3] + 1,每次排序让增量成为原来的三分之一,加一是防止gap <= 3时gap = gap / 3 = 0的发生,导致希尔增量最后不为1,无法完成插入排序。到目前为止业内对于两个大佬的方法依然是看法不一,都没有比出个上下来
我们目前使用的则是Knuth提出的除三法获得希尔增量来演示
三、代码实现
1. 代码实现思路
希尔排序的代码实现比较魔幻,由于我们讲解的希尔排序的思路是将分组进行直接插入排序,就导致我们容易产生疑惑,是不是分多少组就调用多少次插入排序的代码呢,那这代码量不就随着增量的变化而变化了,但是动态代码这个概念听着就让人倍感稀奇。所以我们仅用一次遍历数组的方式就巧妙对每个分组完成单趟排序,不需要对代码做那样鬼畜的操作
当我们以希尔增量开始遍历时,由于一次跨gap访问下一个数据,所以我们用i变量从0遍历到size-gap-1处,即红色箭头处 
i=0时,我们用end变量从后往前遍历插入,将end+gap作为下一个数据的位置,此时end+gap数据大于end处数据,原地插入(不做插入)即可。(g箭头指向end+gap处的数据) 
i++,end再次往前遍历,找end+gap处数据该插入的位置,6依然大于3,不做插入 
i接着向后遍历,end变量找end+gap处数据该插入的位置,2依然大于4,不做插入 
i还是遍历,end变量向前找到end+gap处数据的插入位置,7比8小,end向前移动gap位,将该数据插入到此时的end+gap位置 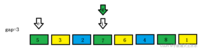
i遍历到下一个,此时end+gap为1,比6小,end向前移动gap位,将该数据插入到此时的end+gap位置此时end+gap为1,依然比end处的3小,end继续减gap,在end+gap处继续插入(此时end < 0,但是我们以end+gap作为插入位置,所以不会造成数组越界) 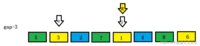

i不用动了,刚好到size-gap-1处,循环结束,第一趟遍历就结束了 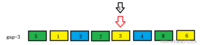
gap = gap / 3 + 1,gap = 1,接着插入排序,直到排序完成 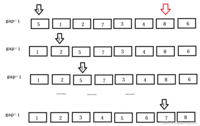
这个过程相当于对每个分组按照一个固定顺序轮流插入排序,并且它们是以一个元素为单位同时进行的,而不是先将某个分组插入排序完再下一个分组。
2. 实现代码
void ShellSort(int* arr, int size){ int gap = size; while (gap > 1) { gap = gap / 3 + 1;//调整希尔增量 int i = 0; for (i = 0; i < size - gap; i++)//从0遍历到size-gap-1 { int end = i; int temp = arr[end + gap]; while (end >= 0) { if (arr[end] > temp) { arr[end + gap] = arr[end]; end -= gap; } else { break; } } arr[end + gap] = temp;//以 end+gap 作为插入位置 } }}