目录
前言
1.用差分法求解
显示差分
其他方程举例 :
r是什么
2.PDETOOL
3.pdepe函数
示例:热方程
代码:
前言
在我们处理一些公式时,常常会有偏微分方程出现,所以我今天整理了一下求解偏微分方程的常用方法,希望有所帮助
在1979年复旦大学学者的一篇论文里,谈到了偏微分方程所需要的条件
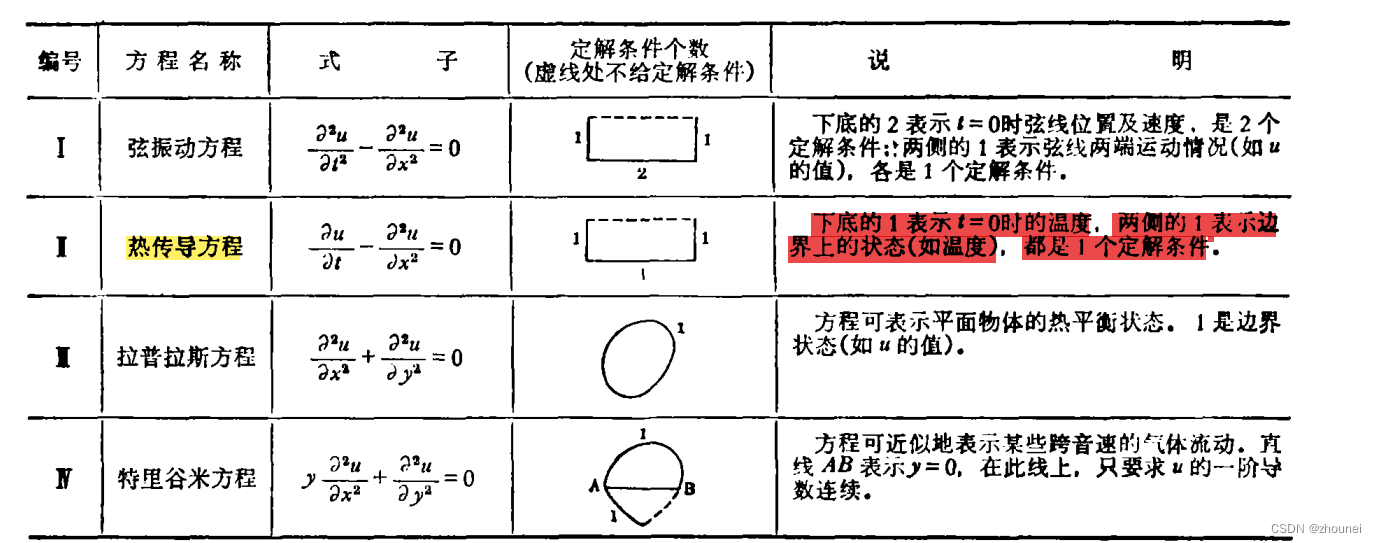
即在下图中我们求解热传导方程

热以箭头方向传导,我们需要知道初始温度,以及边界温度(上下面的温度)我们以热传导方程
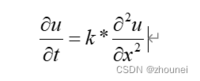
为例,
1.用差分法求解
显示差分
显式差分方法(Explicit Finite Difference Method)是一种常用的数值方法,用于求解偏微分方程。它基于将偏微分方程中的导数项转化为有限差分的形式,并使用离散化的网格来逼近连续的空间和时间域。
显式差分方法中,通过使用中心差分来近似空间导数项,并使用向前差分或向后差分来近似时间导数项。其中,向前差分是使用当前时间步的数据来近似时间导数,而向后差分是使用下一个时间步的数据来近似时间导数。
对于扩散方程的求解,显式差分方法可以使用如下的差分方程形式:
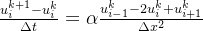
在matlab
u(k+1, i) =u(k, i) + r * (u(k, i-1) - 2 * u(k, i) + u(k, i+1))
默认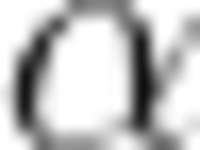 =1
=1
其中,u(k+1, i) 表示下一个时间步 t_{k+1} 和空间位置 x_i 处的值,u(k, i) 表示当前时间步 t_k 和空间位置 x_i 处的值,r 为时间步长和空间步长的比值。
k 表示时间步数索引,即第 k 个时间步。通常,时间步长为 dt,那么第 k 个时间步的时间值为 t_k = k * dt。
i 表示空间步数索引,即第 i 个空间步。通常,空间步长为 dx,那么第 i 个空间步的位置值为 x_i = i * dx。
显式差分方法的优点是简单易实现,但其稳定性需要满足一个数值稳定性条件,即 r 小于一个特定的临界值。当 r 超过该临界值时,数值解可能会出现不稳定和振荡现象。
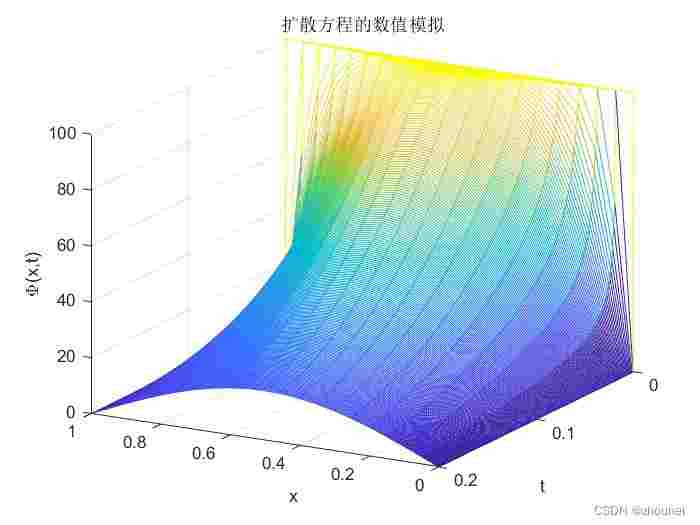
clearclcclose all dx=0.05; %x方向的步长dt=0.001; %t方向的步长r=dt/(dx^2); %计算r的值x=0:dx:1; %得到x的序列t=0:dt:0.2; %得到t的序列M=length(x)-1;N=length(t)-1;u=ones(N+1,M+1);u(1,:)=100; %设置初值条件:u(x,0)=100u(2:N+1,1)=0; %设置边界条件:u(0,t)=0u(2:N+1,M+1)=0; %设置边界条件:u(1,t)=0%根据差分方程,计算u的数值解for k=1:N for i=2:M u(k+1,i)=(1-2*r)*u(k,i)+r*(u(k,i-1)+u(k,i+1)); endend[x,t]=meshgrid(x,t);mesh(x,t,u) %绘制(x,t,u)的三维图xlabel('x')ylabel('t')zlabel('\u(x,t)')title('扩散方程的数值模拟')u(x,0)=100 1
u(0,t)=0 2
u(1,t)=0 3
是限制条件,具体解释一下就是,
1.在t=0时,函数u在空间位置 x 处的值为 100 ,即初始温度为100°
2.上下温度均为0,换句话说,u在 x = 0 处的边界条件被设定为 0,在 x = 1 处的边界条件被设定为 0
所以,这个意思就是温度在长方形中间部位温度达到最高,随后逐渐消散变为0
其他方程举例 :
对于二维泊松方程:
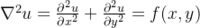
差分方程:
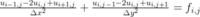
对于一维对流-扩散方程:
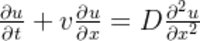
差分方程:
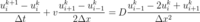
matlab代码:
u(k+1, i) = u(k, i) - r * (v * (u(k, i+1) - u(k, i-1)) / (2*dx) - D * (u(k, i-1) - 2*u(k, i) + u(k, i+1)) / dx^2)
clc,clear% 设置参数和网格v = ...; % 对流速度D = ...; % 扩散系数dt = ...; % 时间步长dx = ...; % 空间步长x = x_min:dx:x_max; % 网格上的位置数组t = 0:dt:t_max; % 网格上的时间数组% 计算稳定性条件r = (v * dt) / (2 * dx);% 初始化数值解u = zeros(length(t), length(x)); % 数值解的矩阵u(1, :) = ...; % 初始条件设置% 遍历时间步for k = 1:length(t)-1 % 遍历空间步 for i = 2:length(x)-1 % 根据差分方程计算数值解 u(k+1, i) = u(k, i) - r * (v * (u(k, i+1) - u(k, i-1)) / (2*dx) - D * (u(k, i-1) - 2*u(k, i) + u(k, i+1)) / dx^2); endend% 绘制数值解mesh(x, t, u);xlabel('x');ylabel('t');zlabel('u(x,t)');title('一维对流-扩散方程的数值解');r是什么
在这个问题中,r 是一个常数,它代表时间步长和空间步长的比值。 使用该值可以控制数值方法的稳定性和精度。
具体而言,在扩散方程的数值求解中,使用显式差分方法时,我们使用差分近似来代替偏微分方程中的导数项。而差分近似的准确性和稳定性取决于时间步长和空间步长的选择。
常见的稳定性要求是在进行数值模拟时确保 r 值小于或等于0.5。这被称为CFL条件(Courant-Friedrichs-Lewy条件)。
r 的计算公式如下:
r = dt / (dx^2)
其中 dt 是时间步长(时间间隔),dx 是空间步长(空间间隔)。
通过计算 r 的值,我们可以选择合适的时间步长和空间步长,以控制数值方法的稳定性和精度。
2.PDETOOL
如果你是高手,自然也会使用pdetool这个工具,直接在命令行窗口调用,绘图然后输入条件,最后导出数据,由于过程太麻烦,我就不再说了,大家可以参看这位的文章
MATLAB 偏微分方程工具箱 pdetool 入门教程 - 知乎 (zhihu.com)
3.pdepe函数
这个函数时matlab自带的,也是matlab帮助中心所运用的
示例:热方程
尝试此示例
抛物型 PDE 的一个示例是一维热方程:
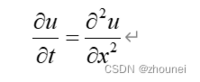
此方程描述 0≤x≤L 和 t≥0 的散热情况。目标是求解 u(x,t) 温度问题。温度最初是一个非零常量,因此初始条件是
u(x,0)=T0.
此外,左边界的温度为零,右边界的温度不为零,因此边界条件为
u(0,t)=0,
u(L,t)=1.
要在 MATLAB 中求解该方程,需要对方程、初始条件和边界条件编写代码,然后在调用求解器 pdepe 之前选择合适的解网格。
编写方程代码
在编写方程代码之前,您需要确保它的形式符合 pdepe 求解器的要求:
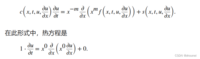
因此,系数的值如下:
m=0
c=1
f=∂u/∂x
s=0
m 的值作为参数传递给 pdepe,而其他系数编写为方程的一个函数,即
function [c,f,s] = heatpde(x,t,u,dudx)c = 1;f = dudx;s = 0;end
在这里默认k=1,我们可以加上k
function [c,f,s] = heatpde(x,t,u,dudx)k = 0.663; % 热传导系数c = 1;f = k * dudx;s = 0;end

p,q值由上述边界条件得出
代码:
function [c,f,s] = heatpde(x,t,u,dudx)c = 1;f = dudx;s = 0;endfunction u0 = heatic(x)u0 = 0.5;%初始温度endfunction [pl,ql,pr,qr] = heatbc(xl,ul,xr,ur,t)pl = ul;ql = 0;pr = ur - 1;qr = 0;end选择解网格
使用包含 20 个点的空间网格和包含 30 个点的时间网格。由于解快速达到稳态,t=0 附近的时间点间隔更近以将此行为捕获到输出中。
L = 1;x = linspace(0,L,20);t = [linspace(0,0.05,20), linspace(0.5,5,10)];求解方程
最后,使用对称性值 m、PDE 方程、初始条件、边界条件以及 x 和 t 的网格来求解方程。
m = 0;sol = pdepe(m,@heatpde,@heatic,@heatbc,x,t);对解进行绘图
使用 imagesc 可视化解矩阵。
colormap hotimagesc(x,t,sol)colorbarxlabel('Distance x','interpreter','latex')ylabel('Time t','interpreter','latex')title('Heat Equation for $0 \le x \le 1$ and $0 \le t \le 5$','interpreter','latex')希望有所帮助!