?博客主页: 【小扳_-CSDN博客】
❤感谢大家点赞?收藏⭐评论✍


文章目录
1.0 判断合法
1.1 使用遍历方式实现验证二叉搜索树
1.2 使用递归方式实现验证二叉搜索树
2.0 求范围和
2.1 使用非递归实现二叉搜索树的范围和
2.2 使用递归方式实现二叉搜索树的范围和
3.0 根据前序遍历结果建树
3.1 使用非递归实现前序遍历构造二叉搜索树
3.2 使用递归实现前序遍历构造二叉搜索树
4.0 二叉搜索树的最近祖先
4.1 使用遍历方式实现二叉搜索树的最近公共祖先
5.0 本篇二叉搜索树实现 LeetCode 经典题的完整代码
1.0 判断合法
题目:
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
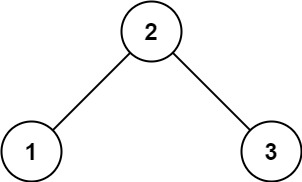
输入:root = [2,1,3]输出:true
OJ链接:98. 验证二叉搜索树
1.1 使用遍历方式实现验证二叉搜索树
具体思路为:利用中序遍历的效果,若每一个节点的值都比前一个节点的值大,则符合二叉搜索树;若出现某一个节点或者多个节点的值比前一个节点的值大,则符合二叉搜索树。
代码如下:
//使用遍历实现验证二叉树 public boolean isValidBST2(TreeNode node) { Stack<TreeNode> stack = new Stack<>(); TreeNode p = node; long prev = Long.MIN_VALUE; while (p != null || !stack.isEmpty()) { if (p != null) { stack.push(p); p = p.left; }else { TreeNode pop = stack.pop(); if(pop.val <= prev) { return false; } prev = pop.val; p = pop.right; } } return true; }需要注意的是,当前节点的值等于前一个节点的值时,同样是不属于二叉搜索树。
1.2 使用递归方式实现验证二叉搜索树
具体思路为:利用递归遍历该二叉树时,先对节点的左子树进行操作,若该左子树返回的是 true 时,则继续判断当前节点的值 val ;若该左子树返回的是 false 时,则不需要再进行下去了,返回 false 结束。若当前当前节点的值小于前一个节点的值,则返回 false ;若当前节点的值大于前一个节点时,需要将 prev = node.val 赋值完后,继续判断下去。直到遇到 node == null 时,返回 true 。若左子树与当前的节点都为 true 时,接着到该节点的右子树。最后当且仅当,左右子树都为 true 时,说明该二叉树是属于二叉搜索树。
代码如下:
//使用递归实现验证二叉树 private long prev = Long.MIN_VALUE; public boolean isValidBST(TreeNode root) { if(root == null) { return true; } boolean l = isValidBST(root.left); if (!l) { return false; } if(prev >= root.val) { return false; } prev = root.val; return isValidBST(root.right); }
2.0 求范围和
题目:
给定二叉搜索树的根结点 root,返回值位于范围 [low, high] 之间的所有结点的值的和。
示例 1:
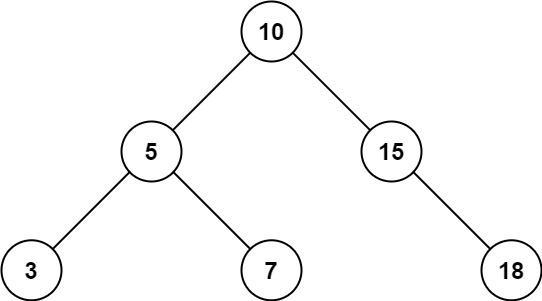
输入:root = [10,5,15,3,7,null,18], low = 7, high = 15输出:32
OJ链接:938. 二叉搜索树的范围和
2.1 使用非递归实现二叉搜索树的范围和
具体思路为:利用中序遍历效果,对于满足 node.val > slow && node.val < high 的节点 node 将该节点的 node.val 累加到 sum 中,直到遇到 node.val > high 时,则直接返回 sum 结果即可。
代码如下:
//使用非递归求二叉搜索树的范围和 public int rangeSum2(TreeNode root,int slow,int high) { Stack<TreeNode> stack = new Stack<>(); TreeNode p = root; int sum = 0; while(p != null || !stack.isEmpty()) { if(p != null) { stack.push(p); p = p.left; }else { TreeNode pop = stack.pop(); if(pop.val > high) { break; } if(pop.val >= slow) { sum += pop.val; } p = pop.right; } } return sum; }
2.2 使用递归方式实现二叉搜索树的范围和
具体思路为:首先考虑符合 slow 与 high 范围之内的节点值,需要返回当前节点的值与该节点的左子树与右子树的符合范围的节点值。再来考虑不符合 slow 与 high 范围之内的节点值时,当 node.val < slow ,则不能再往该节点的左子树继续递归下去了,需要往该节点的右子树递归下去;当 node.val > slow ,则不能往该节点的右子树继续递归下去了,需要往该节点的左子树递归寻找符合范围值的节点。
代码如下:
//使用递归求二叉搜索树的范围和 public int rangeSum(TreeNode root,int slow, int high) { if(root == null) { return 0; } if(root.val < slow) { return rangeSum(root.right,slow,high); } if(root.val > high) { return rangeSum(root.left,slow,high); } return root.val + rangeSum(root.left,slow,high) + rangeSum(root.right,slow,high); }
3.0 根据前序遍历结果建树
题目:
给定一个整数数组,它表示BST(即 二叉搜索树 )的 先序遍历 ,构造树并返回其根。
保证 对于给定的测试用例,总是有可能找到具有给定需求的二叉搜索树。
二叉搜索树 是一棵二叉树,其中每个节点, Node.left 的任何后代的值 严格小于 Node.val , Node.right 的任何后代的值 严格大于 Node.val。
二叉树的 前序遍历 首先显示节点的值,然后遍历Node.left,最后遍历Node.right。
示例 1:
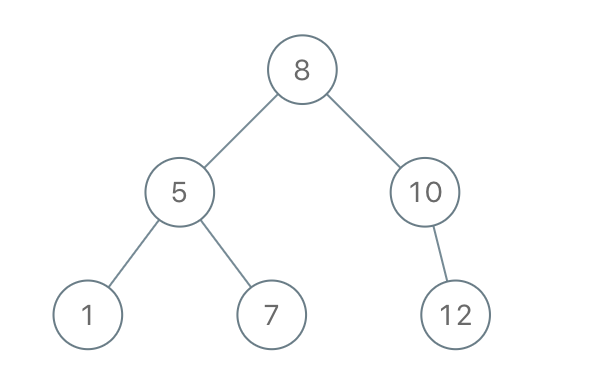
输入:preorder = [8,5,1,7,10,12]输出:[8,5,10,1,7,null,12]
OJ链接:1008. 前序遍历构造二叉搜索树
3.1 使用非递归实现前序遍历构造二叉搜索树
具体思路为:利用数组中第一个值作为根节点的值,再遍历数组从索引 1 开始直到该数组长度 - 1 。得到每一个数组的值来创建一个新的节点,再自定义 insert 方法将该节点插入二叉搜索树中。关键的是:使用非递归方式实现该方法,首先定义一个 parent 变量,用来记录 p 的父亲节点,循环遍历 p ,若 p.val > node.val 时,先记录 parent = p,再 p = p.left ;若 p.val < node.val 时, 先记录 parent = p,再 p = p.right 。直到 p == null 时,跳出循环,则当前的 parent 就是该二叉树的叶子节点,在判断 node.val 与 parent.val 的大小关系,若 node.val > parent.val,则 parent.right = node;若 node.val < parent.val,则 parent.left = node 。
代码如下:
//根据前序遍历的结果建树 public TreeNode bstFromPreorder(int[] preorder) { TreeNode root = new TreeNode(preorder[0]); for(int i = 1; i < preorder.length; i++) { TreeNode p = new TreeNode(preorder[i]); insert(root,p); } return root; } //使用非递归的方式 public void insert(TreeNode root, TreeNode node) { TreeNode p = root; TreeNode parent = null; while(p != null) { if(p.val < node.val) { parent = p; p = p.right; }else if(p.val > node.val) { parent = p; p = p.left; } } if(parent.val > node.val) { parent.left = node; }else { parent.right = node; } }
3.2 使用递归实现前序遍历构造二叉搜索树
具体思路为:递归遍历直到遇到 node == null 时,那么 node = new TreeNode(val) 。若 node.val > val 时,向左子树递归下去 node = node.left;若 node.val < val 时,先右子树递归下去 node = node.right 。每一次递归完,返回的时候,需要重新链接当前节点的左子树或者右子树,再返回当前节点。
代码如下:
//根据前序遍历的结果建树 public TreeNode bstFromPreorder(int[] preorder) { TreeNode root = new TreeNode(preorder[0]); for(int i = 1; i < preorder.length; i++) { TreeNode p = new TreeNode(preorder[i]); insert(root,p); } return root; }//使用递归的方式 public TreeNode insert(TreeNode node, int val) { if (node == null) { return new TreeNode(val); } if (node.val > val) { node.left = insert(node.left,val); }else { node.right = insert(node.right,val); } return node; }
4.0 二叉搜索树的最近祖先
题目:
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
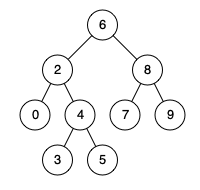
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8输出: 6 解释: 节点 2 和节点 8 的最近公共祖先是 6。
OJ链接:235. 二叉搜索树的最近公共祖先
4.1 使用遍历方式实现二叉搜索树的最近公共祖先
具体思路为:若 p 与 q 在当前节点的左右子树,那么该节点就是该 q 与 p 的公共最近的祖先;若 p 与 q 在当前节点的同一侧(都在该当前节点的左子树或者右子树),则需要继续往下遍历,当 node.val < p.val && node.val < q.val 或者 node.val > p.val && node.val > q.val 都需要继续遍历,直到跳出循环后,则当前节点 node 就是该 p 与 q 的公共最近节点。
代码如下:
//二叉搜索树的最近祖宗 public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { TreeNode a = root; while(p.val < a.val && q.val < a.val || p.val > a.val && q.val > a.val) { if(p.val < a.val) { a = a.left; }else { a = a.right; } } return a; }
5.0 本篇二叉搜索树实现 LeetCode 经典题的完整代码
import java.util.Stack;public class TreeNode { int val; TreeNode left; TreeNode right; TreeNode() {} TreeNode(int val) { this.val = val; } TreeNode(int val, TreeNode left, TreeNode right) { this.val = val; this.left = left; this.right = right; } //使用递归实现验证二叉树 private long prev = Long.MIN_VALUE; public boolean isValidBST(TreeNode root) { if(root == null) { return true; } boolean l = isValidBST(root.left); if (!l) { return false; } if(prev >= root.val) { return false; } prev = root.val; return isValidBST(root.right); } //使用遍历实现验证二叉树 public boolean isValidBST2(TreeNode node) { Stack<TreeNode> stack = new Stack<>(); TreeNode p = node; long prev = Long.MIN_VALUE; while (p != null || !stack.isEmpty()) { if (p != null) { stack.push(p); p = p.left; }else { TreeNode pop = stack.pop(); if(pop.val <= prev) { return false; } prev = pop.val; p = pop.right; } } return true; } //使用递归求二叉搜索树的范围和 public int rangeSum(TreeNode root,int slow, int high) { if(root == null) { return 0; } if(root.val < slow) { return rangeSum(root.right,slow,high); } if(root.val > high) { return rangeSum(root.left,slow,high); } return root.val + rangeSum(root.left,slow,high) + rangeSum(root.right,slow,high); } //使用非递归求二叉搜索树的范围和 public int rangeSum2(TreeNode root,int slow,int high) { Stack<TreeNode> stack = new Stack<>(); TreeNode p = root; int sum = 0; while(p != null || !stack.isEmpty()) { if(p != null) { stack.push(p); p = p.left; }else { TreeNode pop = stack.pop(); if(pop.val > high) { break; } if(pop.val >= slow) { sum += pop.val; } p = pop.right; } } return sum; } //根据前序遍历的结果建树 public TreeNode bstFromPreorder(int[] preorder) { TreeNode root = new TreeNode(preorder[0]); for(int i = 1; i < preorder.length; i++) { TreeNode p = new TreeNode(preorder[i]); insert(root,p); } return root; } //使用非递归的方式 public void insert(TreeNode root, TreeNode node) { TreeNode p = root; TreeNode parent = null; while(p != null) { if(p.val < node.val) { parent = p; p = p.right; }else if(p.val > node.val) { parent = p; p = p.left; } } if(parent.val > node.val) { parent.left = node; }else { parent.right = node; } } //使用递归的方式 public TreeNode insert(TreeNode node, int val) { if (node == null) { return new TreeNode(val); } if (node.val > val) { node.left = insert(node.left,val); }else { node.right = insert(node.right,val); } return node; } //二叉搜索树的最近祖宗 public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { TreeNode a = root; while(p.val < a.val && q.val < a.val || p.val > a.val && q.val > a.val) { if(p.val < a.val) { a = a.left; }else { a = a.right; } } return a; }}
本篇为相关二叉搜索树对于 LeetCode 题目的相关解法,希望对你有所帮助。