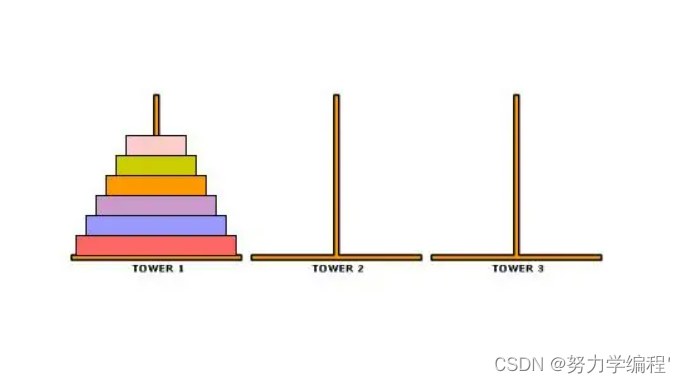
来源及应用
相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如图1)。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。
分析：对于这样一个问题，任何人都不可能直接写出移动盘子的每一步，但我们可以利用下面的方法来解决。设移动盘子数为n，为了将这n个盘子从A杆移动到C杆，可以做以下三步：
(1)以C盘为中介，从A杆将1至n-1号盘移至B杆；
(2)将A杆中剩下的第n号盘移至C杆；
(3)以A杆为中介；从B杆将1至n-1号盘移至C杆。
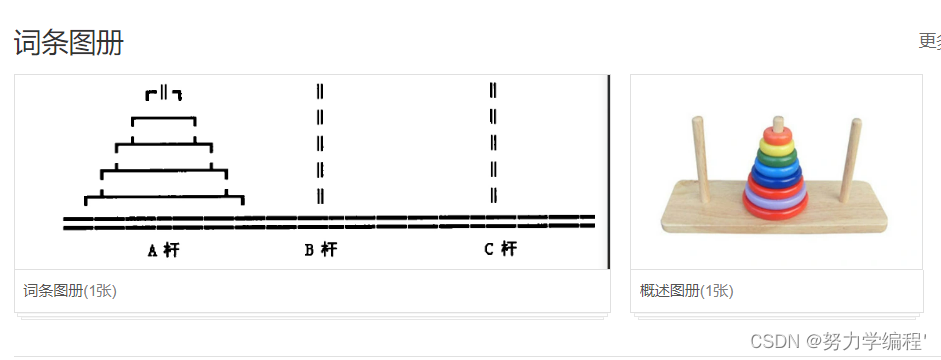
汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。
2020年8月3日，夏焱以33.039秒的成绩成功打破6层汉诺塔吉尼斯世界纪录。 [5-7]
2021年5月16日，中国龙岩的陈诺以29.328秒的成绩打破了6层汉诺塔吉尼斯世界纪录。 [8]
问题解读：
简而言之，这里有三个杆，上面串了n个大小不同的盘，需要将这n个盘经过这三个杆，将全部盘转移到另一个杆上，并且这三个杆在转移的过程中，都要满足杆上的盘要由大到小进行排列。
过程分析
当n等于1时：
只需要挪动一次就好了。
当n等于2时：
仔细思考，不难想到：会经过三个步骤 。
1.A->B
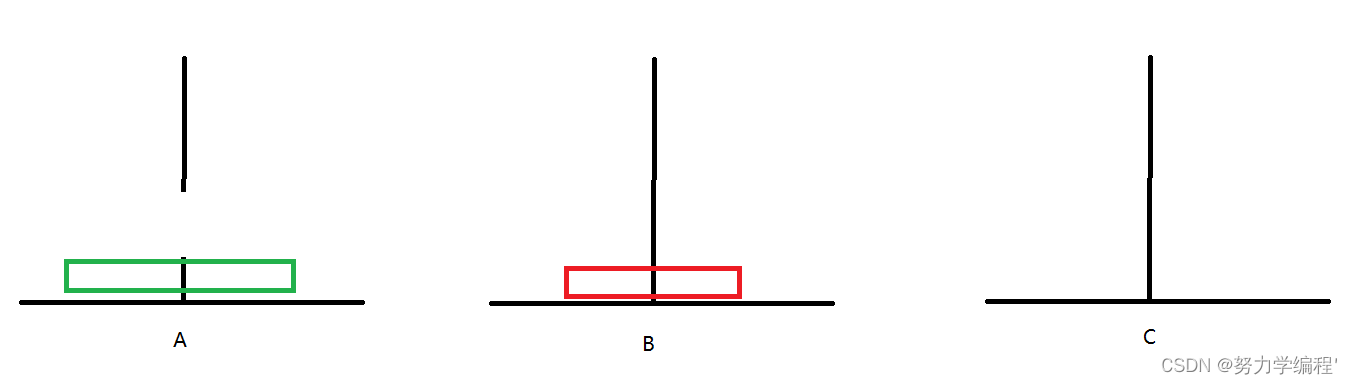
2.A->C
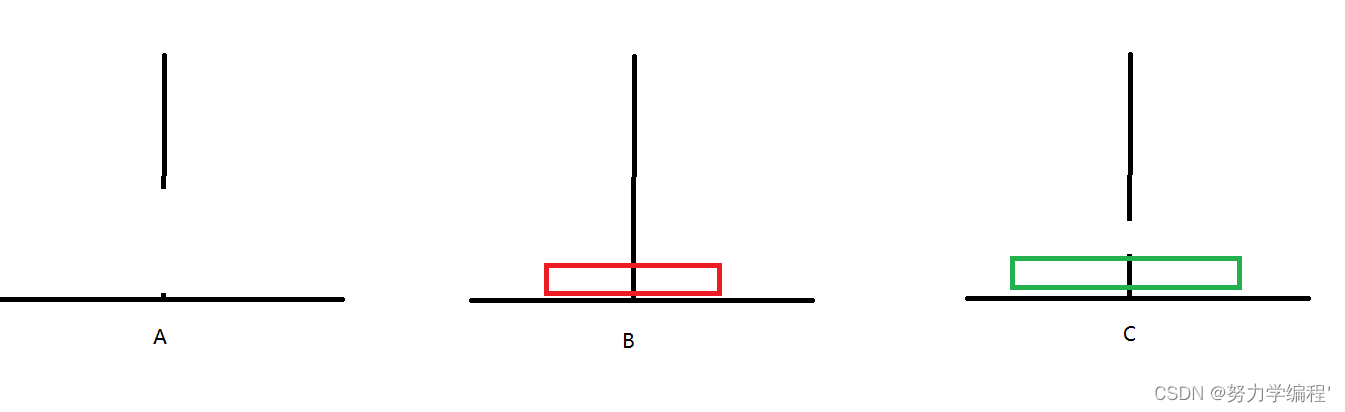
3.B->C
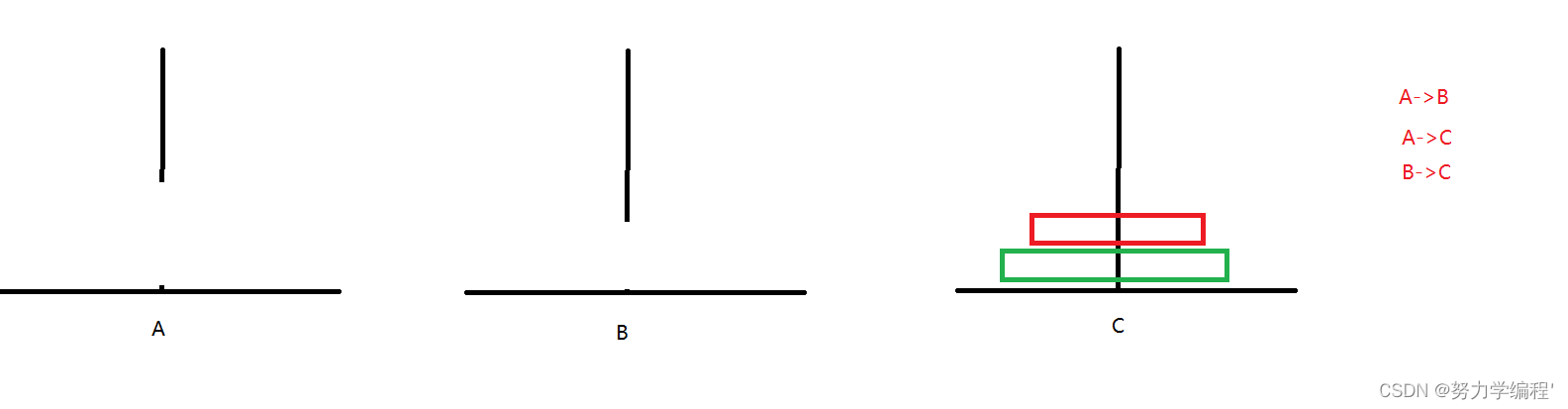
当n等于3时：
同样的道理，我们需要间接的利用这三个杆完成盘子的转移。
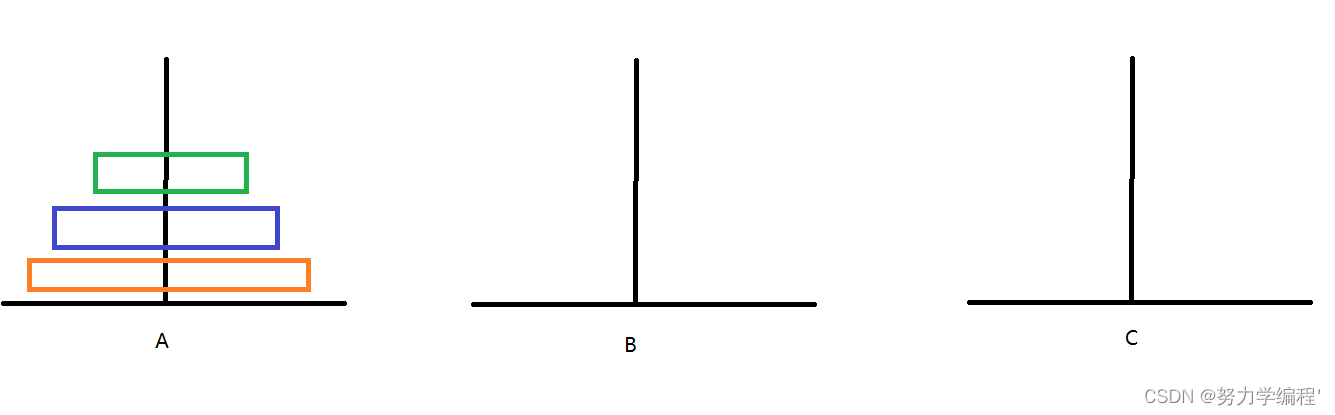
1.A->C,A->B:
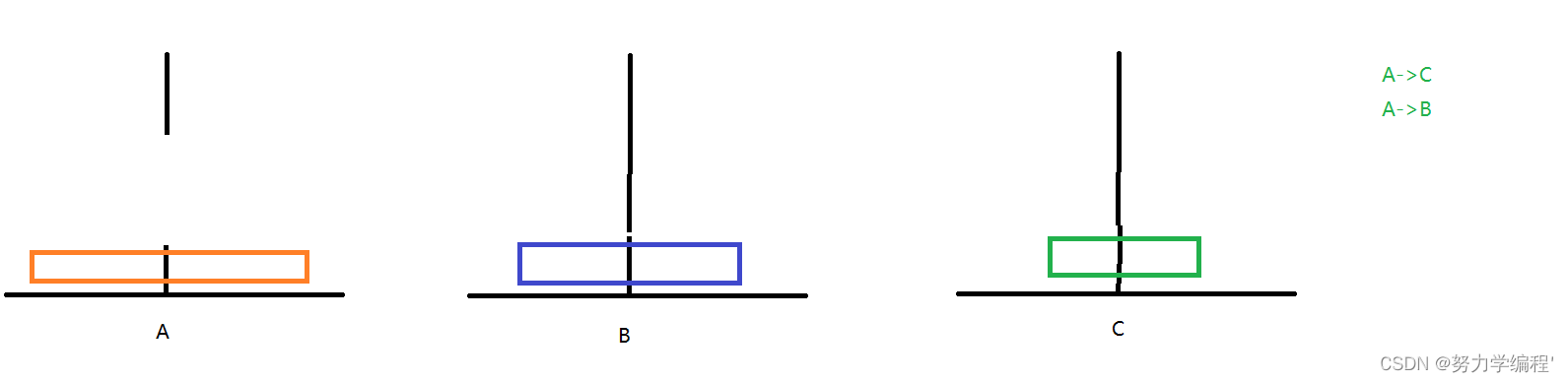
2.C->B,A->C
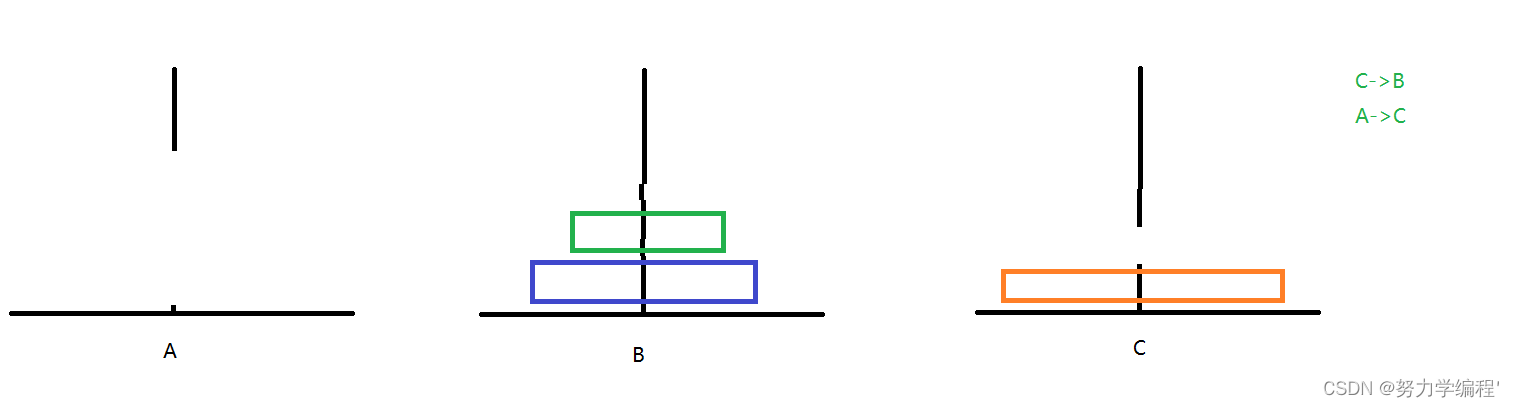
4.B->A,B->C,A->C
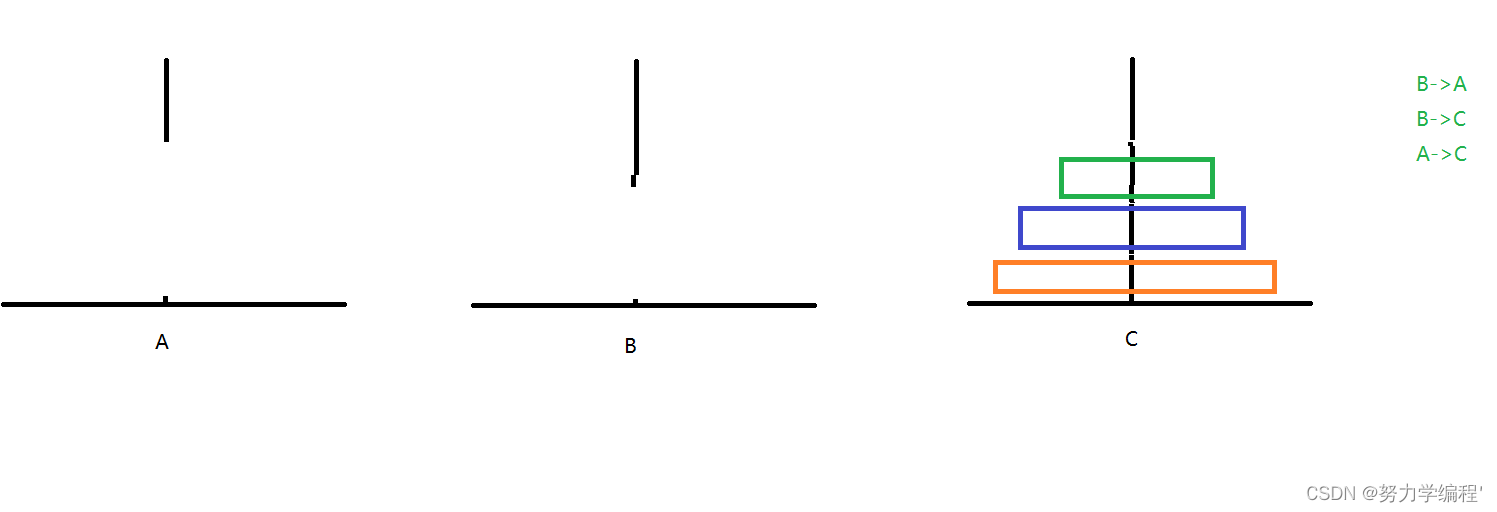最终完成了当n等于3的情况，一共挪动了7步。
解题思路：
通过我们上面对n的分析，我们知道当n等于1时，挪1步，当n等于2时挪3步，当n等于3时，挪动7步，仔细观察不难找到这样一个规律：挪的步数=2^x-1.这样我们就找到了这个问题的突破口。
我们根据n的取值可以将他分为：
具体可以参考当n等于3时进行深入理解。
代码实现：
经过上面的分析，我们就可以利用java中的递归方法来完成汉诺塔问题，如果你对递归有问题的话，可以看一下我的上一篇文章，里面详细介绍了递归的知识，具体实现的时候，利用的就是我们上面找到的规律：
话不多说，直接上代码：
public class Main { public static void move(char pos1,char pos2){ System.out.print(pos1+"->"+pos2+" "); } public static void hanio(int n,char pos1,char pos2,char pos3){ if(n==1){ move(pos1,pos3); } else{ hanio(n-1,pos1,pos3,pos2); move(pos1,pos3); hanio(n-1,pos2,pos1,pos3); } } public static void main(String[] args) { hanio(1,'A','B','C'); System.out.println(); hanio(2,'A','B','C'); System.out.println(); hanio(3,'A','B','C'); System.out.println(); hanio(4,'A','B','C'); }}好了，今天就分享这么多，谢谢大家。
