模型训练后,就要进行模型优化了。
一般来讲,很简单,优化就是不换模型换参数,或者直接换模型。
换了之后来对比,最后选个最好的。
比如在本案例中,选择LinearRegression后,MSE从22下降到12,因此选择新的模型。
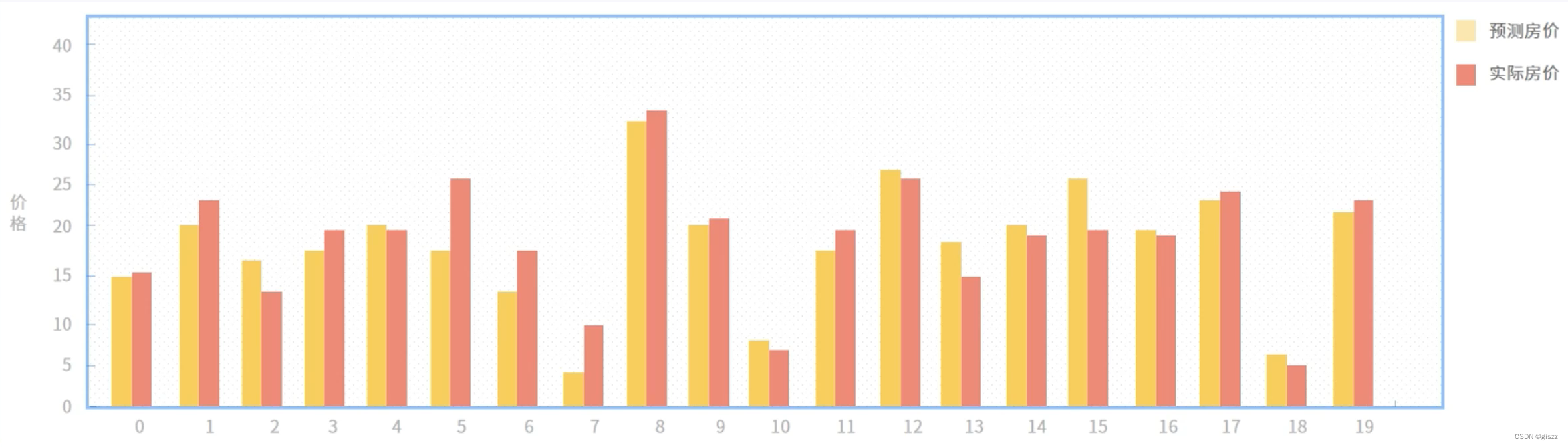
取前20个验证集数据,将标注数据与实际房价对比关系如上图。
可以看到,效果还是很好的。
LinearRegression是线性回归算法。线性回归算法是一种通过对样本特征进行线性组合来进行预测的线性模型,其目的是找到一条直线或一个平面(在多维空间中)来最小化预测值与真实值之间的误差。它假设输入特征与目标变量之间存在线性关系,并通过学习这种关系的权重和截距来进行预测。
线性回归算法的优点:
简单且易于实现:线性回归模型相对简单,计算复杂度低,容易理解和实现。可解释性强:线性回归模型的权重可以直接解释为特征对目标变量的影响程度,有助于理解数据背后的关系。适用于许多场景:线性回归广泛应用于各种领域,如金融、经济、社会科学等,用于预测和解释连续值变量。可作为其他复杂模型的基础:许多复杂的机器学习模型(如神经网络)可以看作是线性模型的扩展或组合。线性回归算法的缺点:
对非线性关系建模能力有限:如果数据之间的关系是非线性的,线性回归模型可能无法很好地拟合数据,导致预测性能下降。对异常值和噪声敏感:线性回归模型容易受到异常值和噪声的影响,这可能导致模型的不稳定或偏差。需要特征选择和预处理:在使用线性回归之前,通常需要进行特征选择和预处理(如标准化、归一化等),以改善模型的性能和稳定性。如果特征选择不当或预处理不充分,可能会影响模型的预测效果。可能过拟合或欠拟合:如果模型过于复杂(即过拟合),它可能会过于关注训练数据中的噪声和细节,导致在新数据上的泛化能力下降。相反,如果模型过于简单(即欠拟合),它可能无法捕捉到数据中的复杂关系,导致预测性能不佳。因此,在选择模型复杂度时需要谨慎权衡。延伸学习:
模型优化的定义:
模型优化是指在机器学习任务中,通过改进模型结构、调整模型参数、优化训练策略等方式,提高模型在特定任务上的性能、效率、稳定性或可解释性的过程。优化的目标可以是降低模型的预测误差、提高模型的泛化能力、减少模型的计算复杂度或增强模型对噪声和异常值的鲁棒性等。
模型优化的步骤:
问题定义与数据准备:明确任务目标,收集并准备相关数据,包括特征工程、数据清洗和预处理等。模型选择与构建:根据任务特点选择合适的算法和模型结构,进行初步的模型构建。模型训练与评估:使用训练数据对模型进行训练,并利用验证数据对模型性能进行评估,包括误差分析、过拟合与欠拟合判断等。模型优化:根据评估结果,采用各种优化技术对模型进行改进,如调整模型参数、改进模型结构、引入正则化等。模型部署与监控:将优化后的模型部署到生产环境,并持续监控模型的性能,及时发现并解决潜在问题。模型优化的关键技术:
特征工程:包括特征选择、特征构造、特征转换等,以提高数据的表达能力和模型的性能。参数调优:通过网格搜索、随机搜索、贝叶斯优化等方法,找到模型的最佳参数配置。模型融合:将多个模型的预测结果进行组合,以提高整体预测性能,如袋装(Bagging)、提升(Boosting)等。正则化技术:通过引入惩罚项来约束模型复杂度,防止过拟合,如L1正则化、L2正则化等。模型压缩与剪枝:通过去除模型中的冗余参数或结构,减小模型大小和计算复杂度,同时保持或接近原始模型的性能。迁移学习:利用在相关领域或任务上预训练的模型作为起点,通过微调适应新任务,加速模型训练和提高性能。自动化机器学习(AutoML):利用算法自动选择模型、调优参数和进行特征工程等,减少人工干预和提高工作效率。模型优化的思路:
从数据出发:深入理解数据特点,挖掘有用特征,去除冗余和噪声信息。先简单后复杂:从简单的模型开始尝试,逐步增加模型复杂度,避免一开始就陷入复杂的模型调整中。实验与对比:通过大量的实验对比不同模型、不同参数配置下的性能差异,找到最佳方案。持续迭代与改进:模型优化是一个持续的过程,需要不断根据实际应用场景和需求进行迭代和改进。关注可解释性:在追求性能的同时,也要关注模型的可解释性,以便更好地理解和信任模型的预测结果。其他重要内容:
评估指标的选择:根据任务类型和目标选择合适的评估指标,如准确率、召回率、F1分数、AUC等,以全面评估模型的性能。交叉验证:使用交叉验证技术来评估模型的稳定性和泛化能力,避免过拟合或欠拟合现象的发生。超参数搜索策略:制定有效的超参数搜索策略,以在合理的计算成本内找到最佳的参数配置。这可以包括手动调整、网格搜索、随机搜索或更高级的搜索算法(如贝叶斯优化)。模型部署的考虑:优化后的模型需要能够顺利地部署到生产环境中,并考虑到实时性、稳定性、安全性等方面的要求。这可能需要与工程团队紧密合作,确保模型的顺利落地和持续监控。