
算法沉淀——队列+宽度优先搜索(BFS)
01.N 叉树的层序遍历02.二叉树的锯齿形层序遍历03.二叉树最大宽度04.在每个树行中找最大值
队列 + 宽度优先搜索算法(Queue + BFS)是一种常用于图的遍历的算法,特别适用于求解最短路径或最少步数等问题。该算法通常用于在图中寻找从起点到目标点的最短路径。
基本思想:
初始化队列: 将起始节点放入队列中。BFS遍历: 从队列中取出一个节点,遍历与该节点相邻且未访问过的节点,将其加入队列。标记已访问: 标记已访问的节点,避免重复访问。重复步骤2和3: 直到队列为空。这个算法适用于无权图的最短路径问题。在搜索的过程中,每一层级的节点都会被依次访问,直到找到目标节点。
具体步骤:
将起始节点加入队列。进行循环直到队列为空: a. 从队列中取出一个节点。 b. 如果该节点是目标节点,返回结果。 c. 否则,将与该节点相邻且未访问过的节点加入队列,并标记为已访问。这种算法适用于许多场景,例如迷宫问题、游戏中的寻路问题、网络路由算法、树问题等。在这些问题中,它能够有效地找到最短路径或最优解。
01.N 叉树的层序遍历
题目链接:https://leetcode.cn/problems/n-ary-tree-level-order-traversal/
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
示例 1: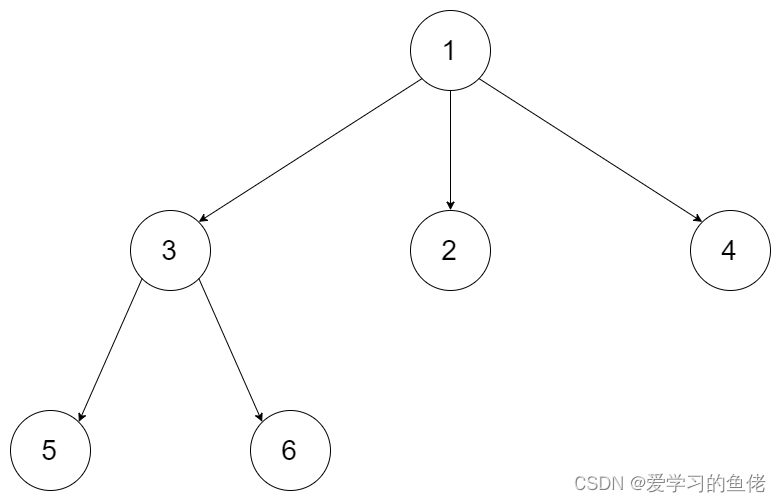
输入:root = [1,null,3,2,4,null,5,6]输出:[[1],[3,2,4],[5,6]]示例 2:
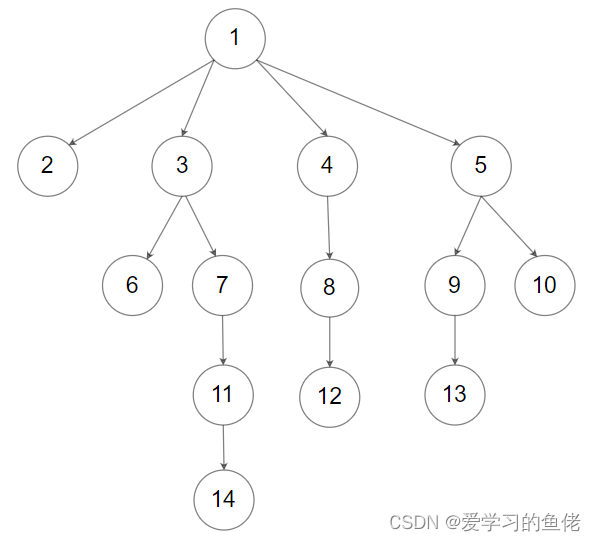
输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]输出:[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]] 提示:
树的高度不会超过1000树的节点总数在 [0, 10^4] 之间 思路
在树的层序遍历中经常要使用到的就是队列和宽度优先搜索算法,这是一道经典的队列和宽度优先搜索算法模板题
初始化一个空的二维向量 ret 用于存储层次遍历的结果。
如果根节点 root 为空,直接返回空向量 ret。
创建一个队列 q 并将根节点入队。
进入主循环,该循环将处理每一层的节点: a. 获取当前队列的大小,即当前层的节点数。 b. 创建一个临时向量 tmp
用于存储当前层的节点值。 c. 对于当前层的每个节点:
出队一个节点t。将节点值 t->val 存入 tmp。将该节点的所有子节点入队,如果子节点非空。 d. 将 tmp 存入 ret。 返回最终的层次遍历结果 ret。
代码
/*// Definition for a Node.class Node {public: int val; vector<Node*> children; Node() {} Node(int _val) { val = _val; } Node(int _val, vector<Node*> _children) { val = _val; children = _children; }};*/class Solution {public: vector<vector<int>> levelOrder(Node* root) { vector<vector<int>> ret; queue<Node*> q; if(!root) return ret; q.push(root); while(q.size()){ int n=q.size(); vector<int> tmp; for(int i=0;i<n;++i){ Node* t=q.front(); tmp.push_back(t->val); for(Node* x:t->children) if(x) q.push(x); q.pop(); } ret.push_back(tmp); } return ret; }};02.二叉树的锯齿形层序遍历
题目链接:https://leetcode.cn/problems/binary-tree-zigzag-level-order-traversal/
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
示例 1:
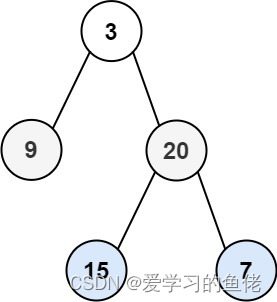
输入:root = [3,9,20,null,null,15,7]输出:[[3],[20,9],[15,7]]示例 2:
输入:root = [1]输出:[[1]]示例 3:
输入:root = []输出:[] 提示:
树中节点数目在范围[0, 2000] 内-100 <= Node.val <= 100 思路
这一题我们仔细理解题意,我们不难发现这题和上一题的区别就是,在偶数行时需要逆序,所以我们只要再添加一个偶数列逆序的操作即可,其余同上。
引入一个标志变量flag,用于标识当前层次是奇数层还是偶数层。初始化为0。初始化一个队列 q 用于层次遍历,以及一个二维向量 ret 用于存储结果。如果根节点 root 为空,直接返回空向量 ret。将根节点入队。进入主循环,该循环处理每一层的节点: a. 获取当前队列的大小,即当前层的节点数,用 s 表示。 b. 递增 flag。 c. 创建一个临时向量 tmp 用于存储当前层的节点值。 d. 对于当前层的每个节点: 出队一个节点 t。将节点值 t->val 存入 tmp。如果节点 t 的左子节点非空,将其入队。如果节点 t 的右子节点非空,将其入队。 e. 如果 flag 为偶数,反转 tmp 中的元素顺序。 f. 将 tmp 存入 ret。 返回最终的层次遍历结果 ret。 代码
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */class Solution {public: vector<vector<int>> zigzagLevelOrder(TreeNode* root) { queue<TreeNode*> q; vector<vector<int>> ret; if(!root) return ret; q.push(root); int flag=0; while(q.size()){ int s=q.size(); flag++; vector<int> tmp; for(int i=0;i<s;++i){ TreeNode* t=q.front(); tmp.push_back(t->val); q.pop(); if(t->left) q.push(t->left); if(t->right) q.push(t->right); } if(flag%2==0) reverse(tmp.begin(),tmp.end()); ret.push_back(tmp); } return ret; }};03.二叉树最大宽度
题目链接:https://leetcode.cn/problems/maximum-width-of-binary-tree
给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
树的 最大宽度 是所有层中最大的 宽度 。
每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
题目数据保证答案将会在 32 位 带符号整数范围内。
示例 1: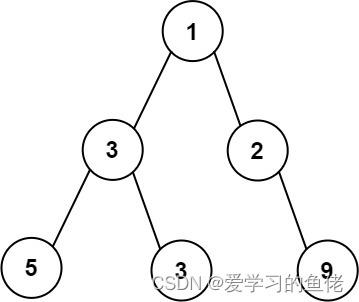
输入:root = [1,3,2,5,3,null,9]输出:4解释:最大宽度出现在树的第 3 层,宽度为 4 (5,3,null,9) 。示例 2: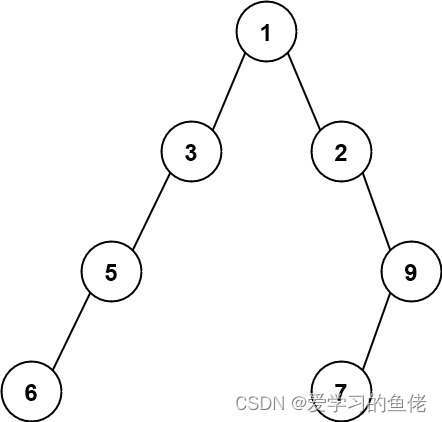
输入:root = [1,3,2,5,null,null,9,6,null,7]输出:7解释:最大宽度出现在树的第 4 层,宽度为 7 (6,null,null,null,null,null,7) 。示例 3: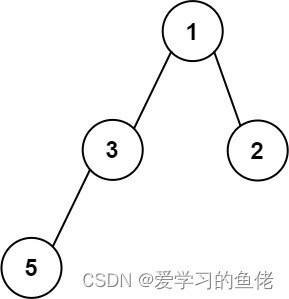
输入:root = [1,3,2,5]输出:2解释:最大宽度出现在树的第 2 层,宽度为 2 (3,2) 。提示:
树中节点的数目范围是[1, 3000]-100 <= Node.val <= 100 思路
这道题最大的坑点在于如果二叉树极度不平衡,若使用模拟的方式,空节点也进行插入操作去计算的话,空间是远远不够的,所以这里我们不能像前面两题这样操作,我们可以通过计算每层插入节点的头和尾下标差值,并使用vector来模拟队列操作,每次都覆盖前一层,以防超出内存,还有计算差值,我们使用无符号整型,这样我们可以避免数据溢出带来的计算错误的值
定义一个队列q,其中每个元素是一个 pair,包含一个二叉树节点指针和该节点在完全二叉树中的编号。将根节点和其对应编号 1 放入队列 q 中。初始化一个变量 ret 用于存储最大宽度。进入主循环,该循环用于遍历二叉树的每一层。 a. 获取当前队列的首尾元素,即队列中最左边和最右边的节点及其编号。 b. 计算当前层的宽度,即 y2 - y1 + 1,其中 y1 是最左边节点的编号,y2 是最右边节点的编号。 c. 更新 ret,取 ret 和当前层宽度的较大值。 d. 创建一个临时队列 tmp。 e. 遍历队列 q 中的每个节点: 如果节点有左子节点,将左子节点及其编号(编号乘以 2)加入 tmp。如果节点有右子节点,将右子节点及其编号(编号乘以 2 加 1)加入 tmp。 f. 将 tmp 赋值给队列 q。 返回最终的宽度 ret。 代码
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */class Solution {public: int widthOfBinaryTree(TreeNode* root) { vector<pair<TreeNode*,unsigned int>> q; q.push_back({root,1}); unsigned int ret=0; while(q.size()){ auto& [x1,y1]=q[0]; auto& [x2,y2]=q.back(); ret=max(ret,y2-y1+1); vector<pair<TreeNode*,unsigned int>> tmp; for(auto& [x,y]:q){ if(x->left) tmp.push_back({x->left,y*2}); if(x->right) tmp.push_back({x->right,y*2+1}); } q=tmp; } return ret; }};04.在每个树行中找最大值
题目链接:https://leetcode.cn/problems/find-largest-value-in-each-tree-row/
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
示例1: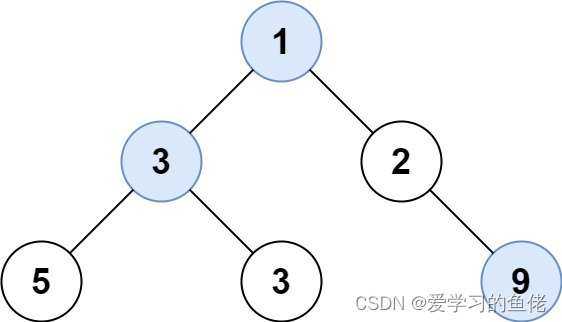
输入: root = [1,3,2,5,3,null,9]输出: [1,3,9]示例2:
输入: root = [1,2,3]输出: [1,3]提示:
二叉树的节点个数的范围是[0,104]-231 <= Node.val <= 231 - 1 思路
根据前面几个题型,我们不难想到,无非就是在层序遍历的基础上增加一个每层的最大值计算,在之前的基础上增加条件即可。
定义一个队列q,其中每个元素是二叉树节点指针。将根节点放入队列 q 中。初始化一个空的数组 ret,用于存储每一层的最大值。进入主循环,该循环用于遍历二叉树的每一层。 a. 初始化一个变量 m 为 INT_MIN,用于记录当前层的最大值。 b. 获取当前队列的大小(即当前层的节点数)。 c. 遍历当前层的每个节点: 弹出队列的首元素,即最左边的节点。更新 m,取 m 和当前节点值的较大值。如果节点有左子节点,将左子节点加入队列 q。如果节点有右子节点,将右子节点加入队列 q。 d. 将 m 添加到数组 ret 中。 返回最终的数组 ret,其中包含了每一层的最大值。 代码
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */class Solution {public: vector<int> largestValues(TreeNode* root) { queue<TreeNode*> q; vector<int> ret; if(!root) return ret; q.push(root); while(q.size()){ int m=INT_MIN; int n=q.size(); for(int i=0;i<n;++i){ auto t=q.front(); q.pop(); m=max(m,t->val); if(t->left) q.push(t->left); if(t->right) q.push(t->right); } ret.push_back(m); } return ret; }};