文章目录
一:卷积的定义二:标准卷积1.1D卷积Ⅰ:一维Full卷积Ⅱ:一维Same卷积Ⅲ:一维Valid卷积Ⅳ:三种一维卷积的相互关系 2.2D卷积3.3D卷积 三:转置卷积四:Separable卷积五:Depthwise卷积六:Pointwise卷积七:扩张/空洞(Dilated/Atrous)卷积
一:卷积的定义
首先,我们首先回顾一下卷积相关的基本概念,定义一个卷积层需要的几个参数。
卷积核大小(Kernel Size):卷积核大小定义了卷积的视野。2维中的常见选择是3 - 即3x3像素矩阵。
步长(Stride):步长定义遍历图像时卷积核的移动的步长。虽然它的默认值通常为1,但我们可以使用值为2的步长来对类似于MaxPooling的图像进行下采样。
填充(Padding):填充定义如何处理样本的边界。Padding的目的是保持卷积操作的输出尺寸等于输入尺寸,因为如果卷积核大于1,则不加Padding会导致卷积操作的输出尺寸小于输入尺寸。
输入和输出通道(Channels):卷积层通常需要一定数量的输入通道(I),并计算一定数量的输出通道(O)。可以通过I * O * K来计算所需的参数,其中K等于卷积核中参数的数量,即卷积核大小。
二:标准卷积
1.1D卷积
一维卷积通常有三种类型:full卷积、same卷积和valid卷积,下面以一个长度为5的一维张量I和长度为3的一维张量K(卷积核)为例,介绍这三种卷积的计算过程。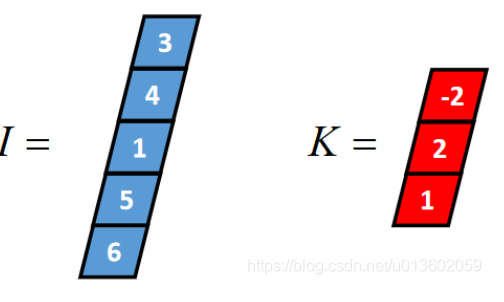
Ⅰ:一维Full卷积
Full卷积的计算过程是:K沿着I顺序移动,每移动到一个固定位置,对应位置的值相乘再求和,计算过程如下: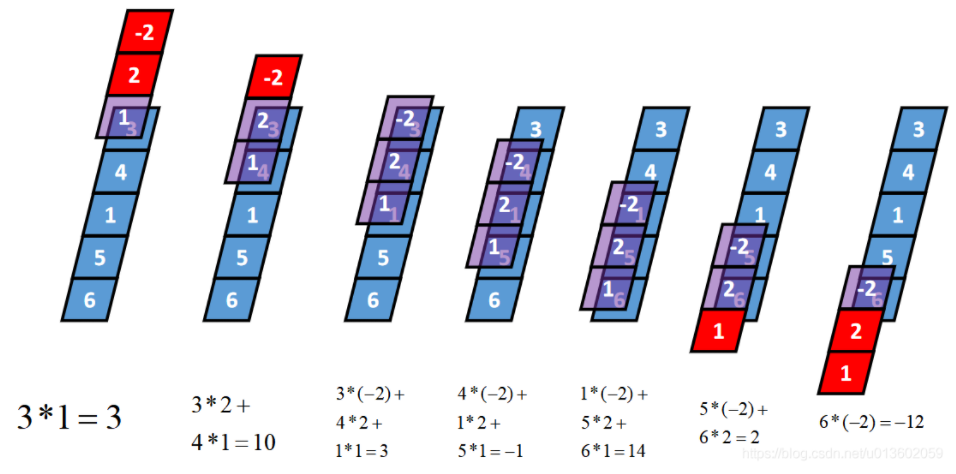
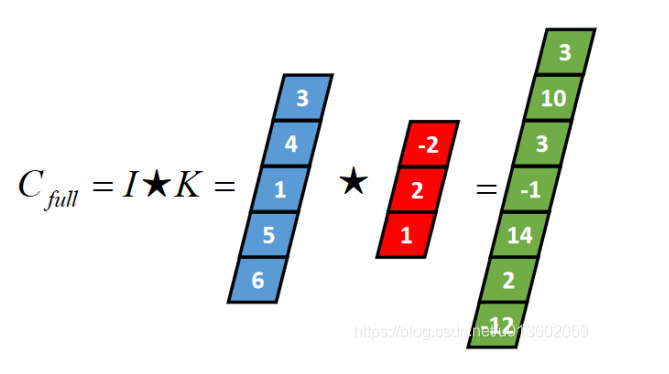
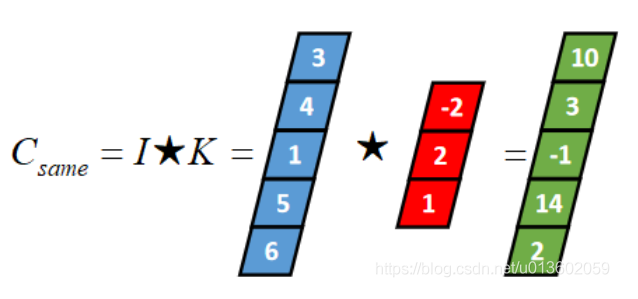
Ⅱ:一维Same卷积
Same卷积核K都有一个锚点,然后将锚点顺序移动到张量I的每一个位置处,对应位置相乘再求和,计算过程如下: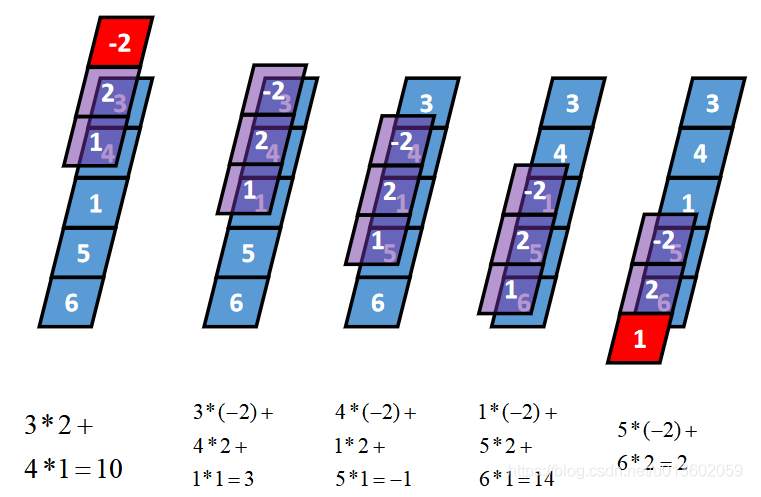
Ⅲ:一维Valid卷积
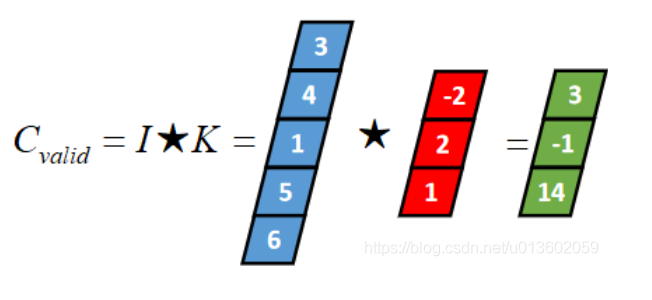
valid卷积只考虑I能完全覆盖K的情况,即K在I的内部移动的情况,计算过程如下: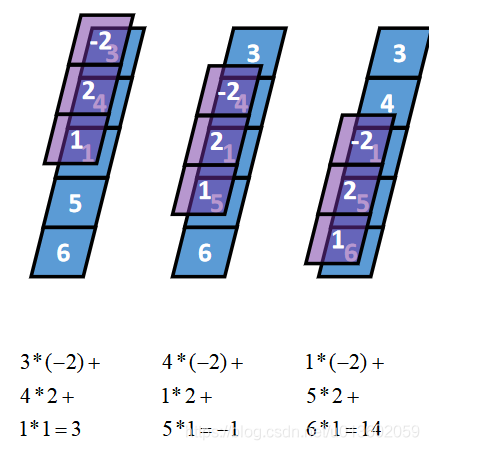
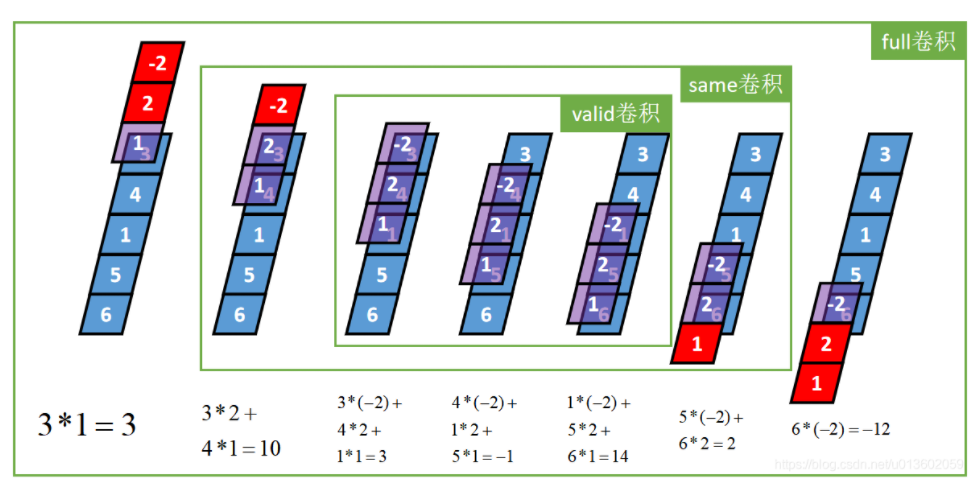
Ⅳ:三种一维卷积的相互关系
2.2D卷积
2D卷积是最常见的卷积,在计算机视觉中大量使用,在此不再赘述。如下图所示: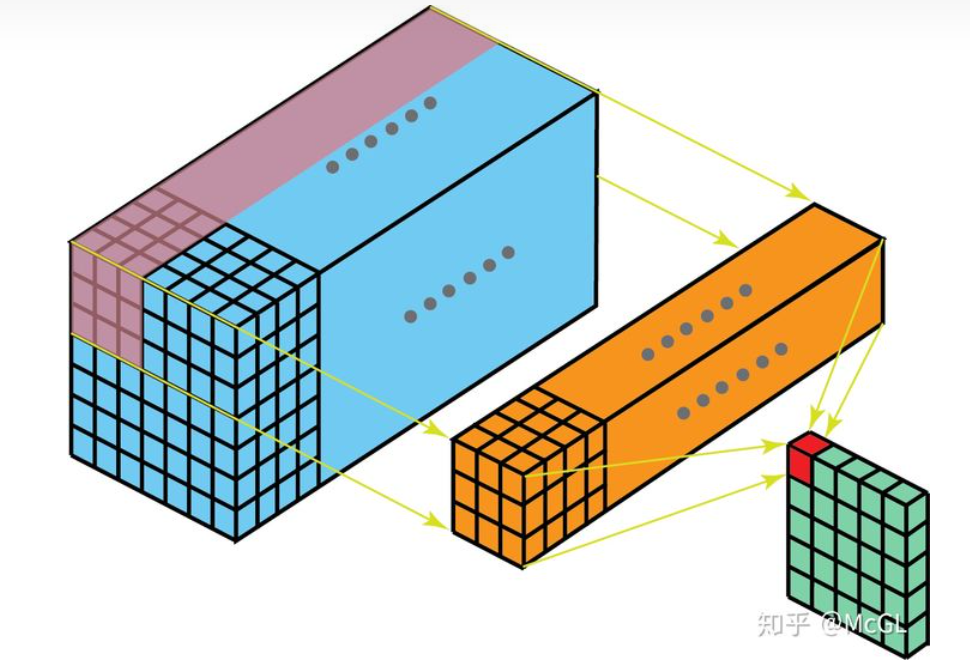
3.3D卷积
在3D卷积中,kernel可以在3个方向上移动,因此获得的输出也是3D。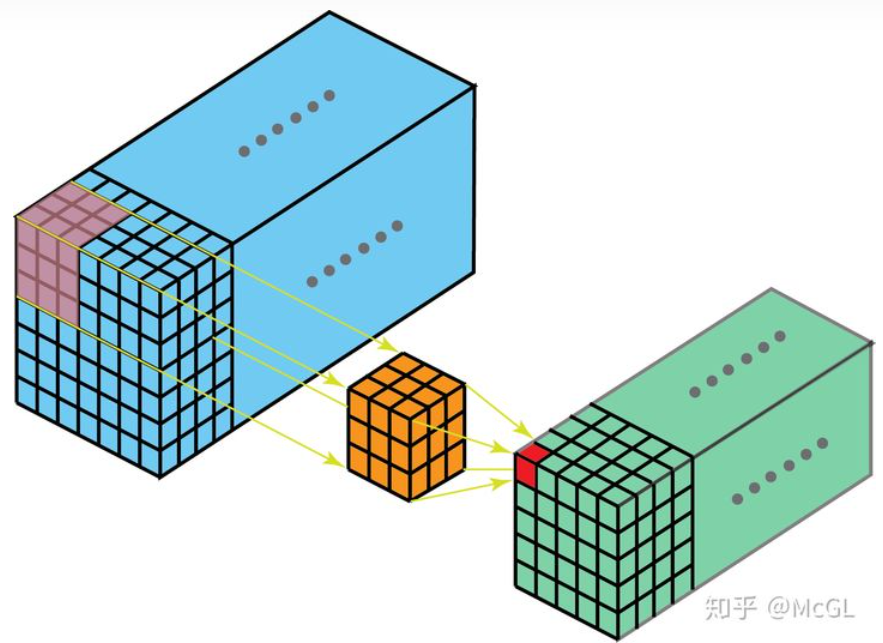
三:转置卷积
有些场景下使用deconvolution,这中说法其实不太合适,因为它不是一个deconvolution,真正的deconvolution应该是卷积操作的逆过程。虽然deconvolution确实存在,但它们在深度学习领域并不常见。想象一下,将图像输入到单个卷积层。现在获得输出,把输出扔到一个黑盒子里,再恢复成的原始输入图像。这个黑盒子才叫做deconvolution。Deconvolution是卷积计算过程的逆计算过程。
转置卷积则比较贴切,因为转置会产生相同的空间分辨率。然而,真实执行的数学运算则稍有不同的。转置卷积层一方面会执行常规卷积,同时也会恢复其空间变换。在执行转置卷积上采样的操作时,要注意棋盘效应
有关转置卷积的讲解,可以看这篇文章
四:Separable卷积
其实就是将filter的K×K×Channel中的Channel(等于输入特征图深度)变为了自己随意设定(当然要小于等于Channel)。
五:Depthwise卷积
它的意思就是拓展Separable convolution而来,我们可以让卷积核的channel维度等于1啊,这样就是深度卷积,意为在每一个channel上做卷积。
六:Pointwise卷积
其实就是点积,就是卷积核大小是1*1的,那为啥起名点积呢?就是因为这和向量中的点积运算很类似。
七:扩张/空洞(Dilated/Atrous)卷积
空洞卷积是解决pixel-wise输出模型的一种常用的卷积方式。一种普遍的认识是,pooling下采样操作导致的信息丢失是不可逆的,通常的分类识别模型,只需要预测每一类的概率,所以我们不需要考虑pooling会导致损失图像细节信息的问题,但是做像素级的预测时(譬如语义分割),就要考虑到这个问题了。那么空洞卷积可以用下图来说明: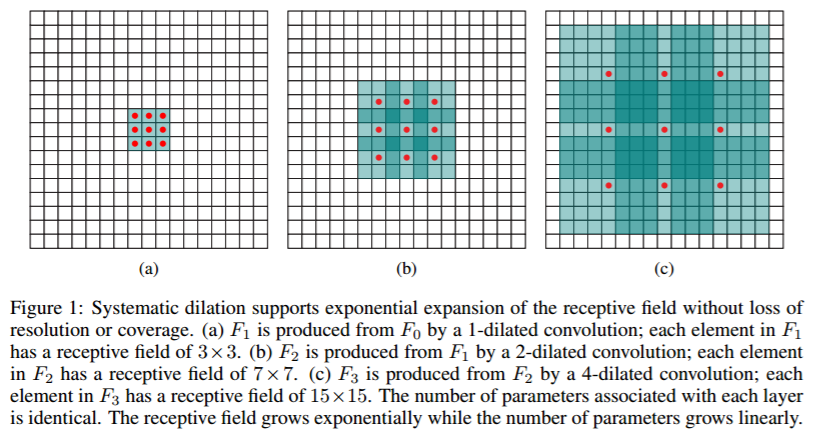
(a)图对应3x3的1-dilated convolution,就是典型的卷积(b)图对应3x3的2-dilated convolution,实际的卷积kernel size还是3x3,但是空洞为1,相当于kernel的size为7x7,图中只有红色点的权重不为0,其余都为0,把3*3的感受野增大到了7*7。(c)图是4-dilated convolution,能达到15x15的感受野。总之,空洞卷积是卷积运算的一种方式,在于增大了感受野却不丢失语义信息。
至此我对深度学习中不同的卷积类型进行了简单讲解,希望对大家有所帮助,有不懂的地方或者建议,欢迎大家在下方留言评论。
我是努力在CV泥潭中摸爬滚打的江南咸鱼,我们一起努力,不留遗憾!