0.写在前面
最小二乘法在工程中得到了广泛的应用,应用最多的是直线拟合(线性拟合),这里做一下总结。首先我们从原理来认识一下线性拟合,然后利用matlab多种方法进行线性参数拟合。
1.原理介绍
给定一系列 x i x_i xi, y i ( i = 1 , 2 , ⋯ , N ) y_i(i=1,2,\cdots,N) yi(i=1,2,⋯,N),假定它们具有线性关系,即可以用 y = k x + b y=kx+b y=kx+b的方式进行拟合,我们的任务是找到最优参数k和b使得 x i x_i xi、 y i y_i yi和直线 y = k x + b y=kx+b y=kx+b最大程度接近,这个时候最小二乘法就派上用场了。
为了描述最小二乘法拟合参数k和b的效果,我们需要定义一个优化函数,为了避免正负相消,所以使用残差(实际观察值与估计值(拟合值)之间的差)平方和来定义:
f = Σ ( y i − k x i − b ) 2 f=\Sigma(y_i-kx_i-b)^2 f=Σ(yi−kxi−b)2
当拟合效果最好时,残差平方和最小是显然的,问题转化为求解 f f f为极值点时, k k k和 b b b为多少?
解决极值点问题,我们需要对 k k k和 b b b分别求偏导数并使其为0:
式(1)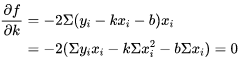
式(2)
由式(2)括号内为0,则有b的表达式:
式(3)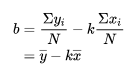
将式(3)代入到式(2)中得到式(4)
式(4)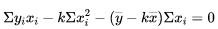
整理式(4)我们可以得到k的表达式:
式(5)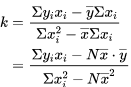
所以最终 k k k和 b b b的表达式可以表示为:
式(6)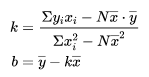
如果用线性代数的角度来看其实矩阵表达更加简洁,我们最终需要寻找最佳的 k k k和 b b b:
式(7)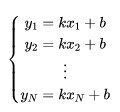
写成矩阵的形式:
式(8)
令

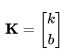
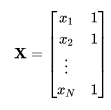
我们可以写成矩阵形式:
式(9)
Y = X K \mathbf{Y}=\mathbf{X}\mathbf{K} Y=XK
我们要解K,这时候X如果是方阵那么自然的就可以左右两边同时乘X的逆,但是如果X不是方阵(行数大于列数),我们可以左右同乘以X的转置,转换为方阵再取逆(当然能取逆的前提是行列式不能为0),具体如下,求得的逆叫做伪逆:
式(10)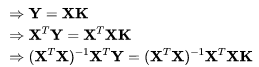
所以解得K的值:
式(11)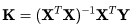
2.matlab实现
现在有这么一组数据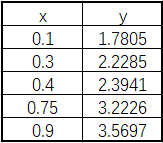
我们利用matlab进行绘制散点图查看一下
x=[0.1;0.3;0.4;0.75;0.9]; y=[1.7805;2.2285;2.3941;3.2226;3.5697];plot(x,y,'o')xlim([0,1]);ylim([1.6,3.7]);hold on;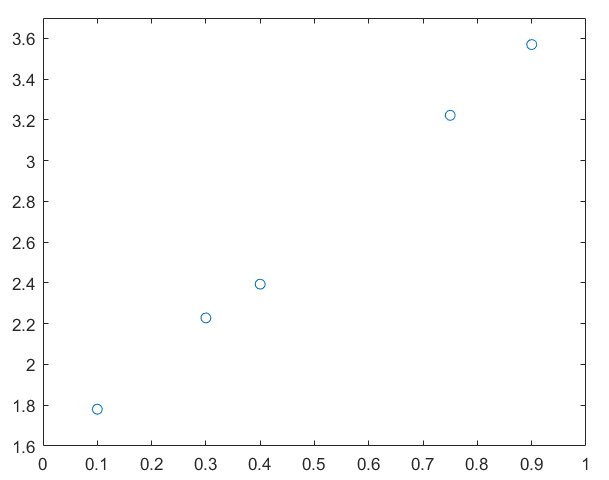
可以看出满足很好的线性关系,下面我们用上述最小二乘法的思想求一下拟合直线的 k k k和 b b b:
方法1:代数方法计算
利用公式(6)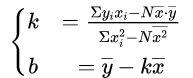
我们来计算一下
% 方法1:代数方法计算N=length(x);k=(sum(y.*x)-N*mean(y)*mean(x))/(sum(x.^2)-N*mean(x)^2);b=mean(y)-k*mean(x);x_line=linspace(0,1,101);y_line=k*x_line+b;plot(x_line,y_line,'Color','r','LineWidth',1)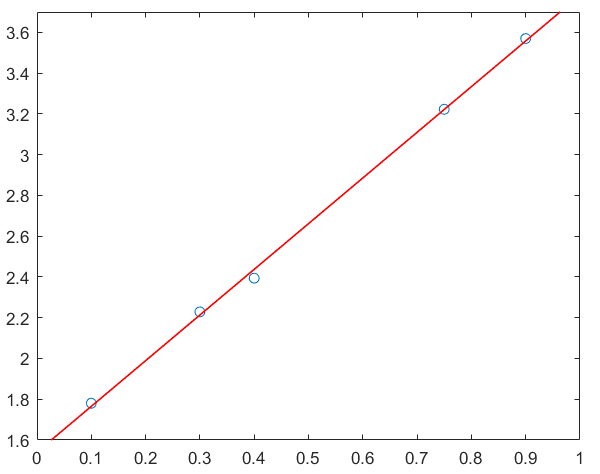
查看k和b的值:
k=2.2411
b=1.5409
方法2:伪逆方法计算
利用公式(11)
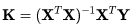
按照前面的原理进行编写:
% 方法2:伪逆计算N=length(x);X=[x,ones(N,1)];Y=y;K=inv(X'*X)*X'*Y;k=K(1);b=K(2);x_line=linspace(0,1,101);y_line=k*x_line+b;plot(x_line,y_line,'Color','r','LineWidth',1)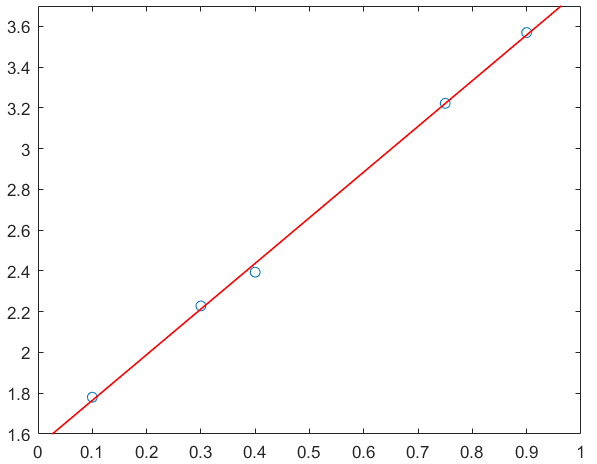
查看k和b的值:
k=2.2411
b=1.5409
方法3:利用matlab自带的lsqcurvefit函数计算(拟合非线性函数,应用更广)
matlab自带的lsqcurvefit函数也可以进行最小二乘拟合(还可以拟合非线性函数),其调用方式为:
各输入参数含义:
我们使用函数的第一种方法进行参数的拟合:
% 方法3:利用matlab自带的lsqcurvefit函数计算fun=@(K,x)K(1)*x+K(2);K0=[1,1];K=lsqcurvefit(fun, K0, x,y)k=K(1);b=K(2);x_line=linspace(0,1,101);y_line=k*x_line+b;plot(x_line,y_line,'Color','r','LineWidth',1)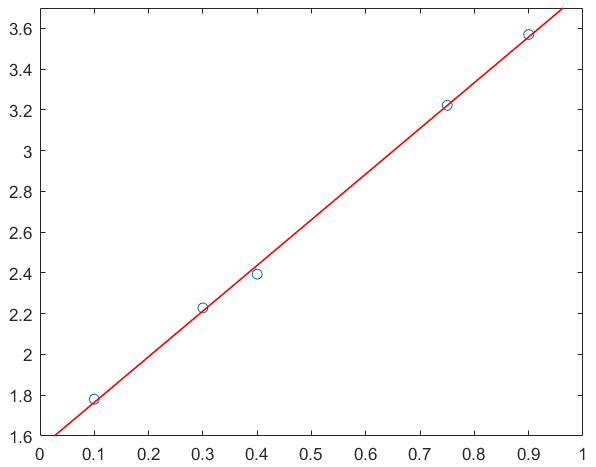 查看k和b的值:
查看k和b的值:
k=2.2411
b=1.5409
方法4:利用matlab自带的polyfit函数计算(多项式函数拟合)
polyfit函数可以用来最小二乘匹配函数。Matlab 包括一个标准函数,对多项式进行最小二乘匹配运算。函数 polyfit 用一系列数据对 N 阶多项式进行最小二乘匹配运算。其中N是任意大于等于1。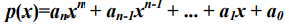
当 N=1 时,得到的是直线方程,得到拟合直线方程的斜率k和b,调用该函数的形式如下:
p = polyfit(x,y,n)
其中xx,y 代表向量 x,y,n 代表阶次,这里我们就选择n=1,然后我们可以编写下面的代码:
K=polyfit(x,y,1);k=K(1);b=K(2);x_line=linspace(0,1,101);y_line=k*x_line+b;plot(x_line,y_line,'Color','r','LineWidth',1)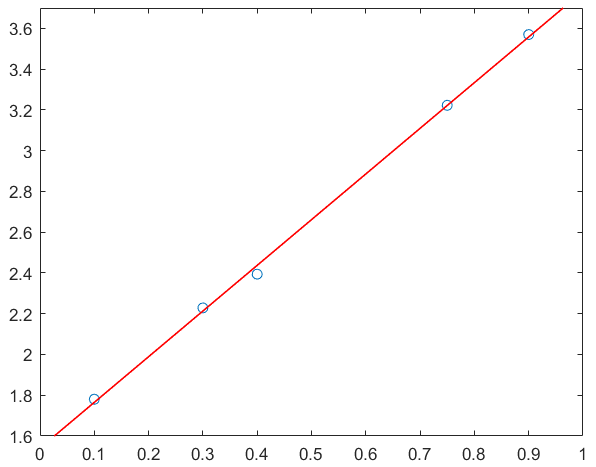 查看k和b的值:
查看k和b的值:
k=2.2411
b=1.5409
结果是一样的。
总结
介绍了最小二乘法拟合直线的两种观点:代数计算和伪逆方法计算,并且利用上述两种方法以及matlab自带的lsqcurvefit和polyfit两种函数使用matlab进行了拟合,可以看到结果是一样的。