一、引言
本文将用matlab编写遗传算法求解TSP旅行商问题,其实是对viafcccy原文章以及《MATLAB智能算法》中基于遗传算法TSP问题复现。但是原文中有一些细节,对像我这样的小白还是有些难度,因此在这里进行重新整理,这里也给出原文链接。
1.1问题描述
旅行商问题(traveling saleman problem, TSP)又被称为推销员问题、货郎担问题,该问题是最基本的路线问题。该问题寻求单一旅行者由起点出发,通过所有给定的需求点之后,最后再回到起点的最小路径成本,路径的限制是每个需求点只能拜访一次。最早的旅行商问题的数学模型是由Dantzig(1959)等学者提出的。旅行商问题是车辆路径问题(VRP)的特例,已证明旅行商问题是NP难问题。
1.2算法实现
1.2.1个体编码
遗传算法中种群个体编码采用正数编码的方式,每个个体表示历经的需求点路线,例如,当总的需求点数量为10,个体的编码可能为[2 3 9 4 8 7 5 6 1 10],表示旅行商从需求点2开始,经过3,9,4,...最终返回需求点2,从而完成TSP遍历。
1.2.2适应度值
种群个体的适应度值表示为遍历路径的长度,计算公式为
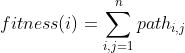
其中,n为城市数量;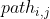 为城市i,j之间的距离。
为城市i,j之间的距离。
1.2.3交叉操作(算法核心之一)
个体之间通过交叉进行更新,交叉方法采用整数交叉法。首先选择两个交叉位置,然后把交叉位置进行互换。此时,产生的两个新个体很有可能存在重复的需求点位置,因此需要进行调整:
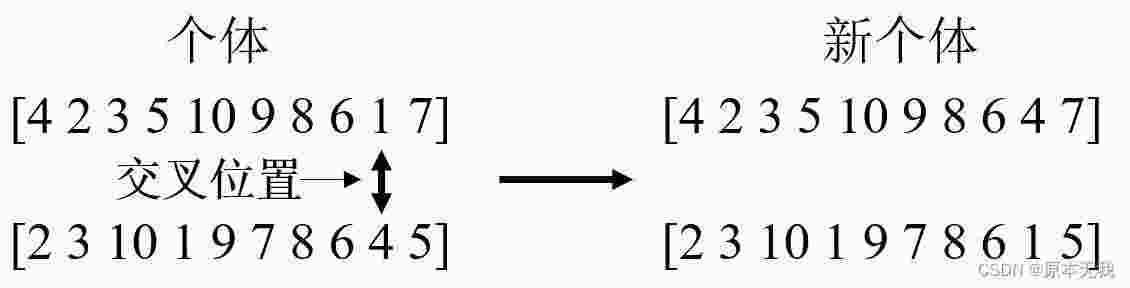
此时交叉后得到的新个体存在重复位置,调整方法为用个体汇总为涵盖的位置代替重复的位置:
1.2.4变异操作(算法核心之二)
TSP问题中为了保证个体变异后,路径仍然满足遍历所有位置,因此采用个体内部两位置互换方法,首先随机选择变异位置pos1和pos2,然后把两个变异位置互换,假设选择的变异位置为9和10,则变异后的新个体为:

对得到的新个体采用保留优秀个体策略,只有当新个体适应度比原来个体好时才进行个体变异。
二、算法实现
2.1城市位置数据
可用如下代码随机生成20个位置数据:
city_location = zeros(20,2);city_location(:,1) = 100 * rand(20,1);city_location(:,2) = 100 * rand(20,1);得到的位置数据如下:
15.761308167754870.604608801960997.05927817606163.1832846377420795.716694824294627.692298496089048.53756487228414.6171390631153980.02804688888009.7131781235847514.188633862721582.345782832729342.176128262627569.482862297581791.573552518906731.709948006086179.220732955955495.022204883835595.94924263929033.4446080502908865.574069915658743.87443596563983.5711678574189638.155845709300884.912930586877776.551678814900293.399324775755179.519990113706367.873515485777418.687260455437975.774013057833348.976439578823174.313246812491644.558620071090039.222701953416864.631301011126565.547789017755770.936483085807317.118668781156275.4686681982361紧接着我们对城市坐标数据进行可视化:
clcclearload("city_location.mat"); % 加在数据location = load("city_location.mat"); % 开始对数据进行可视化x = location.city_location(:,1);y = location.city_location(:,2);plot(x,y,'o');xlabel('城市横坐标');ylabel('城市纵坐标');grid on;计算城市之间的距离:
function D = Distance(a)%计算两两城市之间的距离%输入的数据为所有城市的x、y坐标位置矩阵city_location,输出为两两城市的距离构成的矩阵Drow = size(a,1);D = zeros(row,row);for i = 1:row for j = i+1:row D(i,j) = ((a(i,1)-a(j,1))^2+(a(i,2)-a(j,2))^2)^0.5; D(j,i) = D(i,j); endend2.2遗传算法初始化
遗传算法相关参数设置:
NIND = 100; %种群大小MAXGEN = 500; %最大迭代次数Pc = 0.9; %交叉概率,相当于基因遗传的时候染色体交叉Pm = 0.05; %染色体变异GGAP = 0.9; %这个是代沟,通过遗传方式得到的子代数为父代数*GGAP生成初始种群:
function Chrom = InitPop(NIND,N)%输入:%NIND:种群大小%N:个体染色体长度(城市个数)%输出:初始种群Chrom = zeros(NIND,N); % 定义存储种群的变量for i = 1:NIND Chrom(i,:) = randperm(N);end2.3旅行商路线可视化
可视化旅行商轨迹:
function DrawPath(Chrom,X)%输入:%待画路线%城市的坐标位置%输出:%旅行商的路线 R = [Chrom(1,:) Chrom(1,1)]; %第一个随机解(个体)【Chrom(1,:)取第一行数据】,一共有n个城市,但是这里R有n+1个值,因为后面又补了一个Chrom(1,1),“是为了让路径最后再回到起点”figure;hold onplot(X(:,1),X(:,2),'bo')%X(:,1),X(:,2)分别代表的X轴坐标和Y轴坐标%plot(X(:,1),X(:,2),'o','color',[1,1,1])%X(:,1),X(:,2)分别代表的X轴坐标和Y轴坐标,plot(X(Chrom(1,1),1),X(Chrom(1,1),2),'rv','MarkerSize',20)%标记起点A = X(R,:); %A是将之前的坐标顺序用R打乱后重新存入A中row = size(A,1); %row为坐标数+1for i = 2:row [arrowx,arrowy] = dsxy2figxy(gca,A(i-1:i,1),A(i-1:i,2)); %dsxy2figxy坐标转换函数,记录两个点 annotation('textarrow',arrowx,arrowy,'HeadWidth',5,'color',[0,0,1]);%将这两个点连接起来endhold offxlabel('横坐标x')ylabel('纵坐标y')title('旅行商轨迹图')box on注意这个函数中的dsxy2figxy函数是必须存在的,因为annotation函数中两个点的坐标必须转化在0,1之间
function varargout = dsxy2figxy(varargin) %%将两点坐标值转化至0,1之间if length(varargin{1}) == 1 && ishandle(varargin{1}) ... && strcmp(get(varargin{1},'type'),'axes') hAx = varargin{1}; varargin = varargin(2:end);else hAx = gca;endif length(varargin) == 1 pos = varargin{1};else [x,y] = deal(varargin{:});endaxun = get(hAx,'Units');set(hAx,'Units','normalized'); axpos = get(hAx,'Position');axlim = axis(hAx);axwidth = diff(axlim(1:2));axheight = diff(axlim(3:4));if exist('x','var') varargout{1} = (x - axlim(1)) * axpos(3) / axwidth + axpos(1); varargout{2} = (y - axlim(3)) * axpos(4) / axheight + axpos(2);else pos(1) = (pos(1) - axlim(1)) / axwidth * axpos(3) + axpos(1); pos(2) = (pos(2) - axlim(3)) / axheight * axpos(4) + axpos(2); pos(3) = pos(3) * axpos(3) / axwidth; pos(4) = pos(4) * axpos(4 )/ axheight; varargout{1} = pos;endset(hAx,'Units',axun)编写函数将最优路径输出
function p=OutputPath(R)%打印路线函数%以1->2->3的形式在命令行打印路线 R = [R,R(1)];N = length(R);p = num2str(R(1));for i = 2:N p = [p,'->',num2str(R(i))];enddisp(p)2.4目标函数及适应度函数
目标函数为个体经历的路径总和
function len = PathLength(D,Chrom)%计算所有个体的路线长度%输入%D两两城市之间的距离%Chrom个体的轨迹 [~,col] = size(D); %返回D的列数 NIND = size(Chrom,1);%NIND等于初始种群len = zeros(NIND,1);%初始化一个大小等于NIND的len来记录长度for i = 1:NIND p = [Chrom(i,:) Chrom(i,1)];%构造p矩阵保存路线图 将第一行路线提出 再加上第一个构成回路 i1 = p(1:end-1);%i1从第一个开始遍历到倒数第二个 i2 = p(2:end);%i2从第二个开始遍历到倒数第一个 len(i,1) = sum(D((i1-1)*col+i2));%计算出每种路线(种群的个体)的长度,这里相当于把D矩阵沿行展开end计算个体的适应度,适应度用于评价个体的优劣程度,适应度越大个体越好,反之适应度越小则个体越差,这里将目标值的倒数作为适应度:
function FitnV = Fintness(len) %适应度函数 %输入: %len 个体的长度(TSP的距离) %输出: %FitnV 个体的适应度值 FitnV = 1./len;2.5选择、交叉、变异、重插入
2.5.1选择
这里直接采用原文的方式,尝试编写了轮盘赌代码,失败了。。
function NewChrIx = Sus(FitnV,Nsel)%输入:%FitnV 个体的是适应度值%Nsel 被选个体的数目%输出:%NewChrIx 被选择个体的索引号[Nind,ans] = size(FitnV);%Nind为FitnV的行数也就是个体数 ans为列数1cumfit = cumsum(FitnV);%对适应度累加 例如 1 2 3 累加后 1 3 6 用来计算累积概率trials = cumfit(Nind)/Nsel * (rand + (0:Nsel-1)');%cumfit(Nind)表示的是矩阵cumfit的第Nind个元素 A.'是一般转置,A'是共轭转置 rand返回一个在区间 (0,1) 内均匀分布的随机数%cumfit(Nind)/Nsel平均适应度 * (rand +(0:Nsel-1)')从0开始到89的转置矩阵(行矩阵变列矩阵)加上每一项加上一个0-1的随机数%生成随机数矩阵 用来筛选Mf = cumfit(:,ones(1,Nsel));%将生成的累积概率 复制90份 生成一个100*90的矩阵Mt = trials(:,ones(1,Nind))';[NewChrIx,ans] = find(Mt<Mf & [zeros(1,Nsel);Mf(1:Nind-1,:)]<= Mt);%寻找满足条件的个体 返回返回数组 X 中每个元素的行和列下标[ans,shuf] = sort(rand(Nsel,1));%生成Nsel*1的随机数矩阵 按升序对 A 的元素进行排序 返回选择的shuf 随机打乱个体顺序 保证后续遗传算子操作的随机性NewChrIx = NewChrIx(shuf);%返回shuf索引的矩阵元素编写Select函数
function SelCh = Select(Chrom,FitnV,GGAP)%输入:%Chrom 种群%FitnV 适应度值%GGAP 选择概率%输出:%SelCh 被选择的个体NIND = size(Chrom,1);%种群个体总数NSel = max(floor(NIND * GGAP+.5),2);%确定下一代种群的个体数,如果不足二个就计为二个ChrIx = Sus(FitnV,NSel);SelCh = Chrom(ChrIx,:);2.5.2 交叉
交叉分为两部分,首先是两个个体之间的交叉规则,要保证每个个体遍历需求点:
function [a,b] = intercross(a,b)%输入:%a和b为两个待交叉的个体%输出:%a和b为交叉后得到的两个个体L = length(a);%随机产生交叉区段r1 = randsrc(1,1,[1:L]); % 这里先随机选出两个位置,位置不能超过r2 = randsrc(1,1,[1:L]); % if r1~=r2 a0 = a; b0 = b; s = min([r1,r2]); e = max([r1,r2]); for i = s:e a1 = a; b1 = b; %第一次互换 a(i) = b0(i); b(i) = a0(i); %寻找相同的城市 x = find(a==a(i)); % 如果有相同的城市,x会得到包含i的两个值,y同理 y = find(b==b(i)); %第二次互换产生新的解 i1 = x(x~=i); % 将位置不是i但相同的城市标记出来 i2 = y(y~=i); if ~isempty(i1) a(i1)=a1(i); end if ~isempty(i2) b(i2)=b1(i); % 注意,原文这里有误,应该是b(i2) end endend% 这里增加一段代码,r1=r2时,两个个体只在一点交叉if r1 == r2 a0 = a; b0 = b; a(r1) = b0(r1); b(r1) = a0(r1); x = find(a==a(r1)); y = find(b==b(r1)); i1 = x(x~=r1); i2 = y(y~=r1); if ~isempty(i1) a(i1) = a0(r1); end if ~isempty(i2) b(i2) = b0(r1); endend其次是总的交叉函数
function SelCh = Recombin(SelCh,Pc)%交叉操作%输入:%SelCh 被选择的个体%Pc 交叉概率%输出:%SelCh 交叉后的个体 NSel = size(SelCh,1);for i = 1:2:NSel - mod(NSel,2) % 若不减去余数且NSel如果是奇数,最后一个i会等于NSel,i+1报错 if Pc>=rand %交叉概率PC [SelCh(i,:),SelCh(i+1,:)] = intercross(SelCh(i,:),SelCh(i+1,:)); endend2.5.3 变异
这里选择了一种较为简单的变异方式,去掉了原文逆转的过程,即保证变异后的个体的目标值减小,否则不进行变异:
function SelCh = Mutate(SelCh,D,Pm)%变异操作%输入:%SelCh 被选择的个体%Pm 变异概率%输出:%SelCh 变异后的个体index = SelCh;col = size(SelCh,2); %返回SelCh的列数%lenSelCh = [];lenSelCh = PathLength(D,SelCh);[NSel,L] = size(SelCh);for i = 1:NSel if Pm >= rand R = randperm(L); index(i,R(1:2)) = index(i,R(2:-1:1)); % 将个体i中R(1)和R(2)这两个位置的城市互换 p = [index(i,:) index(i,1)]; i1 = p(1:end-1); i2 = p(2:end); DIndexi = sum(D((i1-1)*col+i2)); % 计算出变异后个体的路径距离 if DIndexi < lenSelCh(i) % 如果变异后路径距离比变异前更小,则保留变异 SelCh(i) = index(i); end endend2.5.4重插入
function Chrom = Reins(Chrom,SelCh,ObjV)%重插入子代的种群%输入:%Chrom 父代的种群%SelCh 子代的种群%ObjV 父代适应度%输出:%Chrom 组合父代与子代后得到的新种群NIND = size(Chrom,1);NSel = size(SelCh,1);[TobjV,index] = sort(ObjV);Chrom = [Chrom(index(1:NIND-NSel),:);SelCh];三、主函数及结果
重新编写了图形输出代码,主函数如下
clcclearload("city_location.mat"); % 加在数据location = load("city_location.mat"); % 开始对数据进行可视化x = location.city_location(:,1);y = location.city_location(:,2);plot(x,y,'o');xlabel('城市横坐标');ylabel('城市纵坐标');%grid on;NIND = 100; %种群大小MAXGEN = 100; %最大迭代次数Pc = 0.9; %交叉概率,相当于基因遗传的时候染色体交叉Pm = 0.05; %染色体变异GGAP = 0.9; %这个是代沟,通过遗传方式得到的子代数为父代数*GGAPD = Distance(city_location); %通过这个函数可以计算i,j两点之间的距离N = size(D,1); %计算有多少个坐标点%%初始化种群Chrom = InitPop(NIND,N); %Chrome代表的种群%%画出随机解得路线图DrawPath(Chrom(1,:),city_location)pause(0.0001)%输出随机解的路线和总距离disp('初始种群中的一个随机值')OutputPath(Chrom(1,:));%其中一个个体Rlength = PathLength(D,Chrom(1,:));disp(['总距离;',num2str(Rlength)]);disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')%优化gen = 0;trace = zeros(1,MAXGEN);title('优化过程')xlabel('迭代次数')ylabel('当前最优解')ObjV = PathLength(D,Chrom);%计算当前路线长度,即上面随机产生的那些个体路径preObjV = min(ObjV);%当前最优解while gen<MAXGEN %%计算适应度 ObjV = PathLength(D,Chrom); %计算路线长度 pause(0.0001); preObjV = min(ObjV); trace(1,gen+1)=preObjV; %trace=[trace preObjV]; FitnV = Fitness(ObjV); %选择 SelCh = Select(Chrom,FitnV,GGAP); %交叉操作 SelCh = Recombin(SelCh,Pc); %变异 SelCh = Mutate(SelCh,D,Pm); Chrom = Reins(Chrom,SelCh,ObjV); gen = gen + 1;end%画出最优解的路线图ObjV = PathLength(D,Chrom); %计算路线长度[minObjV,minInd] = min(ObjV);DrawPath(Chrom(minInd(1),:),city_location)figure();plot([1:MAXGEN],trace(1,:));%%输出最优解的路线和距离disp('最优解:')p = OutputPath(Chrom(minInd(1),:));disp(['旅行商走过的总距离:',num2str(ObjV(minInd(1)))]);disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')所得结果如下:
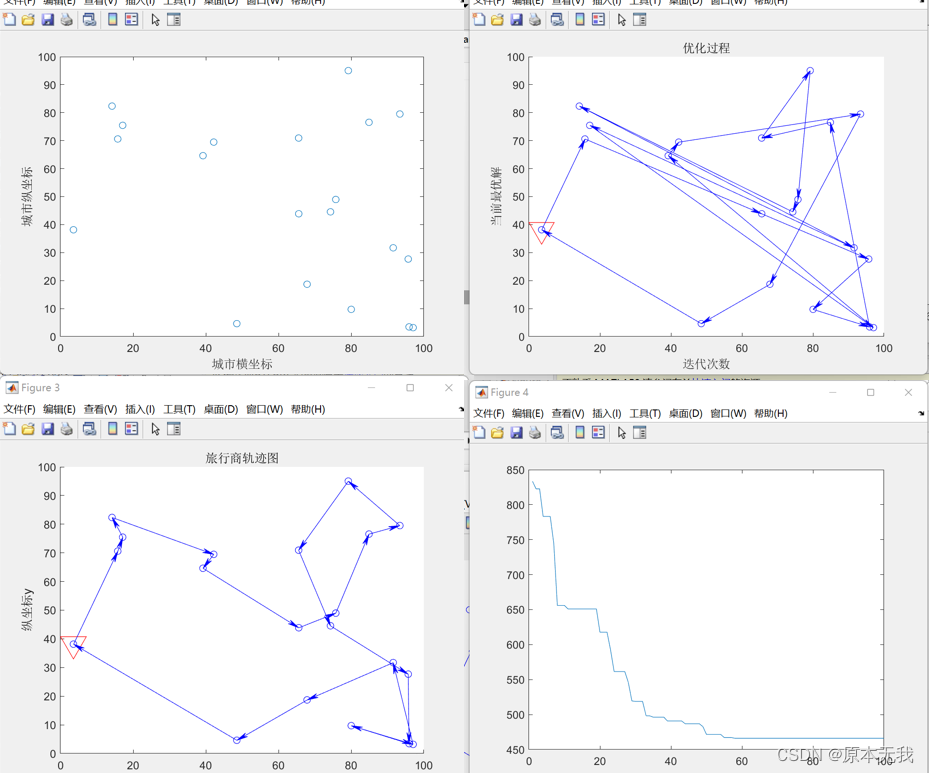
这里需要注意的是,用简化的变异代码求解后,最优解基本在400以上,下面加入逆转算法对模型进行求解。
四、选择、交叉、变异后的逆转
逆转算法的主要思想为,在一个个体中的路径中随机选择两个位置,对中间的城市进行逆转,若逆转后的路径和变小,则保留逆转后的个体,否则不保留。
function SelCh = Reverse(SelCh,D)%进化逆转函数%输入:%SelCh 被选择的个体%D 各城市的距离矩阵%输出:%SelCh 进化逆转后的个体 [row,col] = size(SelCh);ObjV = PathLength(D,SelCh);SelCh1 = SelCh;for i = 1:row r1 = randsrc(1,1,[1:col]); r2 = randsrc(1,1,[1:col]); mininverse = min([r1 r2]); maxinverse = max([r1 r2]); SelCh1(i,mininverse:maxinverse) = SelCh1(i,maxinverse:-1:mininverse);endObjV1 = PathLength(D,SelCh1);%计算路线长度index = ObjV1<ObjV;SelCh(index,:)=SelCh1(index,:);结果如下:
最优解:11->17->8->3->2->10->5->15->4->12->1->20->6->18->7->19->9->14->13->16->11旅行商走过的总距离:379.0725经过多次实验发现,加入逆转过程后,遗传算法的效果明显得到提升。至此,代码已全部完成。
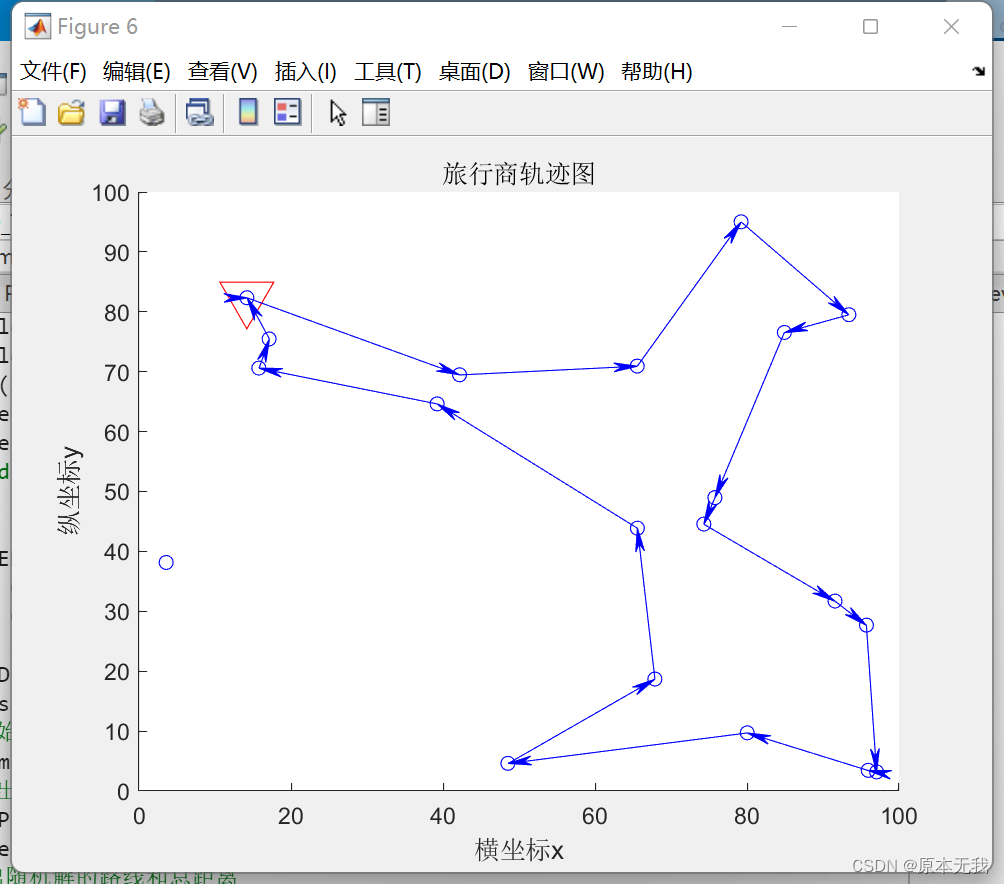
虽然代码复现完成,但是结果有时还是会出现bug,主要存在于得到的最优解中,有时会有一个城市被忽略,不知道问题出在哪里,欢迎大家检验指出。
参考链接
matlab遗传算法(GA)详解(二)旅行商问题(TSP)详解_viafcccy的博客-CSDN博客_旅行商问题matlab算法
《MATLAB智能算法30个案例分析(第二版)》