前言
生成式建模的扩散思想实际上已经在2015年(Sohl-Dickstein等人)提出,然而,直到2019年斯坦福大学(Song等人)、2020年Google Brain(Ho等人)才改进了这个方法,从此引发了生成式模型的新潮流。目前,包括OpenAI的GLIDE和DALL-E 2,海德堡大学的Latent Diffusion和Google Brain的ImageGen,都基于diffusion模型,并可以得到高质量的生成效果。本文以下讲解主要基于DDPM,并适当地增加一些目前有效的改进内容。
基本原理
扩散模型包括两个步骤:
固定的(或预设的)前向扩散过程q:该过程会逐渐将高斯噪声添加到图像中,直到最终得到纯噪声。
可训练的反向去噪扩散过程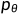 :训练一个神经网络,从纯噪音开始逐渐去噪,直到得到一个真实图像。
:训练一个神经网络,从纯噪音开始逐渐去噪,直到得到一个真实图像。
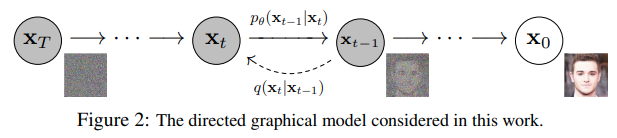
前向与后向的步数由下标 t定义,并且有预先定义好的总步数 T(DDPM原文中为1000)。
t=0 时为从数据集中采样得到的一张真实图片, t=T 时近似为一张纯粹的噪声。
2.1 直观理解
为了看懂扩散模型查了很多资料,但是要么就是大量的数学公式,一行行公式推完了还是不知道它想干啥。要么就是高视角,上来就和能量模型,VAE放一块儿对比说共同点和不同点,看完还是云里雾里。然而事实上下面几句话就能把扩散模型说明白了扩散模型的目的是什么?
学习从纯噪声生成图片的方法
扩散模型是怎么做的?
训练一个U-Net,接受一系列加了噪声的图片,学习预测所加的噪声
前向过程在干啥?
逐步向真实图片添加噪声最终得到一个纯噪声
对于训练集中的每张图片,都能生成一系列的噪声程度不同的加噪图片
在训练时,这些 【不同程度的噪声图片 + 生成它们所用的噪声】 是实际的训练样本
反向过程在干啥?
训练好模型后,采样、生成图片
2.2 数学形式
2.2.1 前向过程
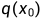 是真实数据分布(也就是真实的大量图片),从这个分布中采样即可得到一张真实图片
是真实数据分布(也就是真实的大量图片),从这个分布中采样即可得到一张真实图片 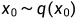 。我们定义前向扩散过程为
。我们定义前向扩散过程为 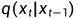 ,即每一个step向图片添加噪声的过程,并定义好一系列
,即每一个step向图片添加噪声的过程,并定义好一系列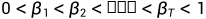 ,则有:
,则有:
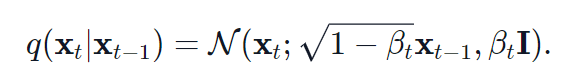
其中,N为正态分布,均值和方差分别为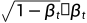 ,因此通过采样标准正态分布
,因此通过采样标准正态分布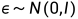 ,有:
,有:
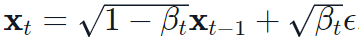



2.2.2 反向过程
那么问题的核心就是如何得到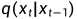 的逆过程
的逆过程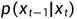 ,这个过程无法直接求出来,所以我们使用神经网络去拟合这一分布。我们使用一个具有参数的神经网络去计算
,这个过程无法直接求出来,所以我们使用神经网络去拟合这一分布。我们使用一个具有参数的神经网络去计算 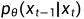 。假设反向的条件概率分布也是高斯分布,且高斯分布实际上只有两个参数:均值和方差,那么神经网络需要计算的实际上是
。假设反向的条件概率分布也是高斯分布,且高斯分布实际上只有两个参数:均值和方差,那么神经网络需要计算的实际上是
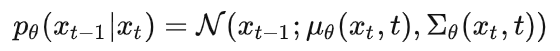
在DDPM中,方差被固定,网络只学习均值。而之后的改进模型中,方差也可由网络学习得到。

2.2.3 总结过程
总之,我们定义这么一个过程:给一张图片逐步加噪声直到变成纯粹的噪声,然后对噪声进行去噪得到真实的图片。所谓的扩散模型就是让神经网络学习这个去除噪声的方法。所谓的加噪声,就是基于稍微干净的图片计算一个(多维)高斯分布(每个像素点都有一个高斯分布,且均值就是这个像素点的值,方差是预先定义的
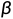 ),然后从这个多维分布中抽样一个数据出来,这个数据就是加噪之后的结果。显然,如果方差非常非常小,那么每个抽样得到的像素点就和原本的像素点的值非常接近,也就是加了一个非常非常小的噪声。如果方差比较大,那么抽样结果就会和原本的结果差距较大。
),然后从这个多维分布中抽样一个数据出来,这个数据就是加噪之后的结果。显然,如果方差非常非常小,那么每个抽样得到的像素点就和原本的像素点的值非常接近,也就是加了一个非常非常小的噪声。如果方差比较大,那么抽样结果就会和原本的结果差距较大。 去噪声也是同理,我们基于稍微噪声的图片
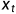 计算一个条件分布,我们希望从这个分布中抽样得到的是相比于
计算一个条件分布,我们希望从这个分布中抽样得到的是相比于 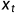 更加接近真实图片的稍微干净的图片。我们假设这样的条件分布是存在的,并且也是个高斯分布,那么我们只需要知道均值和方差就可以了。问题是这个均值和方差是无法直接计算的,所以用神经网络去学习近似这样一个高斯分布。
更加接近真实图片的稍微干净的图片。我们假设这样的条件分布是存在的,并且也是个高斯分布,那么我们只需要知道均值和方差就可以了。问题是这个均值和方差是无法直接计算的,所以用神经网络去学习近似这样一个高斯分布。
2.3 网络训练流程
我们最终要训练的实际上是一个噪声预测器。神经网络输出的噪声是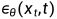 ,而真实的噪声取自于正态分布
,而真实的噪声取自于正态分布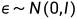 。则损失函数为:
。则损失函数为:
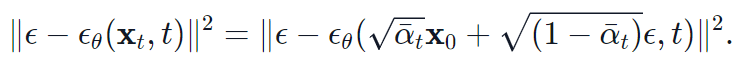
预测网络方面,DDPM采用了 U-Net。
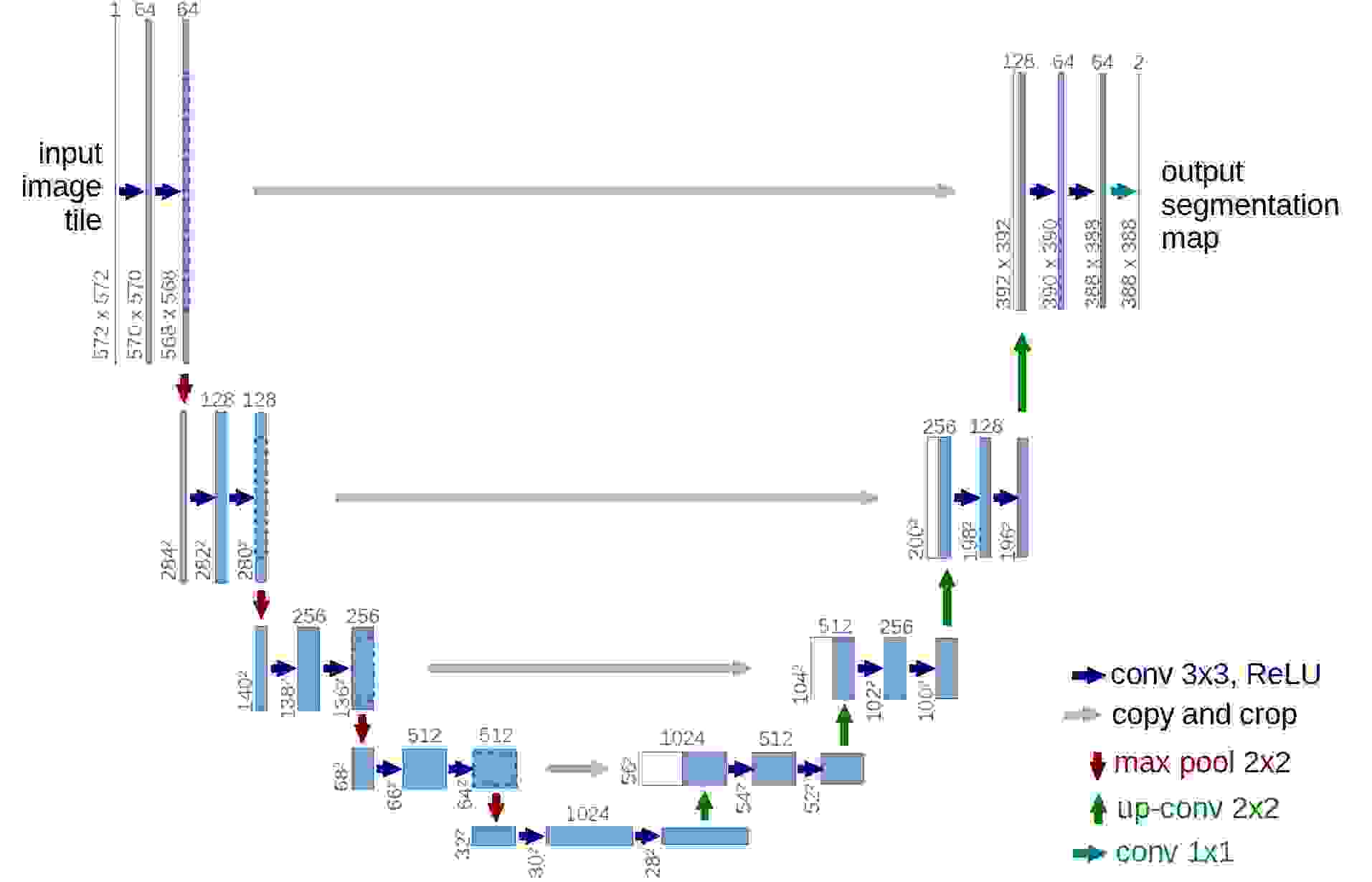
从而,网络的训练流程为:
我们接受一个随机的样本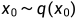 ;
;
我们随机从 1 到 T 采样一个 t;
我们从高斯分布采样一些噪声并且施加在输入上;
网络从被影响过后的噪声图片学习其被施加了的噪声。
代码
3.1 Network helpers
先是一些辅助函数和类。
def exists(x): return x is not None# 有val时返回val,val为None时返回ddef default(val, d): if exists(val): return val return d() if isfunction(d) else d# 残差模块,将输入加到输出上class Residual(nn.Module): def __init__(self, fn): super().__init__() self.fn = fn def forward(self, x, *args, **kwargs): return self.fn(x, *args, **kwargs) + x# 上采样(反卷积)def Upsample(dim): return nn.ConvTranspose2d(dim, dim, 4, 2, 1)# 下采样def Downsample(dim): return nn.Conv2d(dim, dim, 4, 2, 1)3.2 Positional embeddings
类似于Transformer的positional embedding,为了让网络知道当前处理的是一系列去噪过程中的哪一个step,我们需要将步数 t 也编码并传入网络之中。DDPM采用正弦位置编码(Sinusoidal Positional Embeddings)。这一方法的输入是shape为 (batch_size, 1) 的 tensor,也就是batch中每一个sample所处的t ,并将这个tensor转换为shape为 (batch_size, dim) 的 tensor。这个tensor会被加到每一个残差模块中。
class SinusoidalPositionEmbeddings(nn.Module): def __init__(self, dim): super().__init__() self.dim = dim def forward(self, time): device = time.device half_dim = self.dim // 2 embeddings = math.log(10000) / (half_dim - 1) embeddings = torch.exp(torch.arange(half_dim, device=device) * -embeddings) embeddings = time[:, None] * embeddings[None, :] embeddings = torch.cat((embeddings.sin(), embeddings.cos()), dim=-1) return embeddings3.3 ResNet/ConvNeXT block
U-Net的Block实现,可以用ResNet或ConvNeXT。
class Block(nn.Module): def __init__(self, dim, dim_out, groups = 8): super().__init__() self.proj = nn.Conv2d(dim, dim_out, 3, padding = 1) self.norm = nn.GroupNorm(groups, dim_out) self.act = nn.SiLU() def forward(self, x, scale_shift = None): x = self.proj(x) x = self.norm(x) if exists(scale_shift): scale, shift = scale_shift x = x * (scale + 1) + shift x = self.act(x) return xclass ResnetBlock(nn.Module): """Deep Residual Learning for Image Recognition""" def __init__(self, dim, dim_out, *, time_emb_dim=None, groups=8): super().__init__() self.mlp = ( nn.Sequential(nn.SiLU(), nn.Linear(time_emb_dim, dim_out)) if exists(time_emb_dim) else None ) self.block1 = Block(dim, dim_out, groups=groups) self.block2 = Block(dim_out, dim_out, groups=groups) self.res_conv = nn.Conv2d(dim, dim_out, 1) if dim != dim_out else nn.Identity() def forward(self, x, time_emb=None): h = self.block1(x) if exists(self.mlp) and exists(time_emb): time_emb = self.mlp(time_emb) h = rearrange(time_emb, "b c -> b c 1 1") + h h = self.block2(h) return h + self.res_conv(x) class ConvNextBlock(nn.Module): """A ConvNet for the 2020s""" def __init__(self, dim, dim_out, *, time_emb_dim=None, mult=2, norm=True): super().__init__() self.mlp = ( nn.Sequential(nn.GELU(), nn.Linear(time_emb_dim, dim)) if exists(time_emb_dim) else None ) self.ds_conv = nn.Conv2d(dim, dim, 7, padding=3, groups=dim) Get an email address at self.net. It's ad-free, reliable email that's based on your own name | self.net = nn.Sequential( nn.GroupNorm(1, dim) if norm else nn.Identity(), nn.Conv2d(dim, dim_out * mult, 3, padding=1), nn.GELU(), nn.GroupNorm(1, dim_out * mult), nn.Conv2d(dim_out * mult, dim_out, 3, padding=1), ) self.res_conv = nn.Conv2d(dim, dim_out, 1) if dim != dim_out else nn.Identity() def forward(self, x, time_emb=None): h = self.ds_conv(x) if exists(self.mlp) and exists(time_emb): condition = self.mlp(time_emb) h = h + rearrange(condition, "b c -> b c 1 1") h = Get an email address at self.net. It's ad-free, reliable email that's based on your own name | self.net(h) return h + self.res_conv(x)3.4 Attention module
包含两种attention模块,一个是常规的 multi-head self-attention,一个是 linear attention variant。
class Attention(nn.Module): def __init__(self, dim, heads=4, dim_head=32): super().__init__() self.scale = dim_head**-0.5 self.heads = heads hidden_dim = dim_head * heads self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False) self.to_out = nn.Conv2d(hidden_dim, dim, 1) def forward(self, x): b, c, h, w = x.shape qkv = self.to_qkv(x).chunk(3, dim=1) q, k, v = map( lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv ) q = q * self.scale sim = einsum("b h d i, b h d j -> b h i j", q, k) sim = sim - sim.amax(dim=-1, keepdim=True).detach() attn = sim.softmax(dim=-1) out = einsum("b h i j, b h d j -> b h i d", attn, v) out = rearrange(out, "b h (x y) d -> b (h d) x y", x=h, y=w) return self.to_out(out)class LinearAttention(nn.Module): def __init__(self, dim, heads=4, dim_head=32): super().__init__() self.scale = dim_head**-0.5 self.heads = heads hidden_dim = dim_head * heads self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False) self.to_out = nn.Sequential(nn.Conv2d(hidden_dim, dim, 1), nn.GroupNorm(1, dim)) def forward(self, x): b, c, h, w = x.shape qkv = self.to_qkv(x).chunk(3, dim=1) q, k, v = map( lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv ) q = q.softmax(dim=-2) k = k.softmax(dim=-1) q = q * self.scale context = torch.einsum("b h d n, b h e n -> b h d e", k, v) out = torch.einsum("b h d e, b h d n -> b h e n", context, q) out = rearrange(out, "b h c (x y) -> b (h c) x y", h=self.heads, x=h, y=w) return self.to_out(out)3.5 Group normalization
DDPM的作者对U-Net的卷积/注意力层使用GN正则化。下面,我们定义了一个PreNorm类,它将被用于在注意力层之前应用groupnorm。值得注意的是,归一化在Transformer中是在注意力之前还是之后应用,目前仍存在着争议。
class PreNorm(nn.Module): def __init__(self, dim, fn): super().__init__() self.fn = fn self.norm = nn.GroupNorm(1, dim) def forward(self, x): x = self.norm(x) return self.fn(x)3.6 Conditional U-Net
现在,我们已经定义了所有的组件,接下来就是定义完整的网络了。
输入:噪声图片的batch+这些图片各自的t。
输出:预测每个图片上所添加的噪声。
Input:a batch of noisy images of shape ( batch_size, num_channels, h, w ) and a batch of steps of shape ( batch_size, 1 )output: a tensor of shape ( batch_size, num_channels, h, w )
具体的网络结构:
首先,输入通过一个卷积层,同时计算step t 所对应的embedding
通过一系列的下采样stage,每个stage都包含:2个ResNet/ConvNeXT blocks + groupnorm + attention + residual connection + downsample operation
在网络中间,应用一个带attention的ResNet或者ConvNeXT
通过一系列的上采样stage,每个stage都包含:2个ResNet/ConvNeXT blocks + groupnorm + attention + residual connection + upsample operation
最终,通过一个ResNet/ConvNeXT blocl和一个卷积层。
class Unet(nn.Module): def __init__( self, dim, init_dim=None, out_dim=None, dim_mults=(1, 2, 4, 8), channels=3, with_time_emb=True, resnet_block_groups=8, use_convnext=True, convnext_mult=2, ): super().__init__() # determine dimensions self.channels = channels init_dim = default(init_dim, dim // 3 * 2) self.init_conv = nn.Conv2d(channels, init_dim, 7, padding=3) dims = [init_dim, *map(lambda m: dim * m, dim_mults)] in_out = list(zip(dims[:-1], dims[1:])) if use_convnext: block_klass = partial(ConvNextBlock, mult=convnext_mult) else: block_klass = partial(ResnetBlock, groups=resnet_block_groups) # time embeddings if with_time_emb: time_dim = dim * 4 self.time_mlp = nn.Sequential( SinusoidalPositionEmbeddings(dim), nn.Linear(dim, time_dim), nn.GELU(), nn.Linear(time_dim, time_dim), ) else: time_dim = None self.time_mlp = None # layers self.downs = nn.ModuleList([]) self.ups = nn.ModuleList([]) num_resolutions = len(in_out) for ind, (dim_in, dim_out) in enumerate(in_out): is_last = ind >= (num_resolutions - 1) self.downs.append( nn.ModuleList( [ block_klass(dim_in, dim_out, time_emb_dim=time_dim), block_klass(dim_out, dim_out, time_emb_dim=time_dim), Residual(PreNorm(dim_out, LinearAttention(dim_out))), Downsample(dim_out) if not is_last else nn.Identity(), ] ) ) mid_dim = dims[-1] self.mid_block1 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim) self.mid_attn = Residual(PreNorm(mid_dim, Attention(mid_dim))) self.mid_block2 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim) for ind, (dim_in, dim_out) in enumerate(reversed(in_out[1:])): is_last = ind >= (num_resolutions - 1) self.ups.append( nn.ModuleList( [ block_klass(dim_out * 2, dim_in, time_emb_dim=time_dim), block_klass(dim_in, dim_in, time_emb_dim=time_dim), Residual(PreNorm(dim_in, LinearAttention(dim_in))), Upsample(dim_in) if not is_last else nn.Identity(), ] ) ) out_dim = default(out_dim, channels) self.final_conv = nn.Sequential( block_klass(dim, dim), nn.Conv2d(dim, out_dim, 1) ) def forward(self, x, time): x = self.init_conv(x) t = self.time_mlp(time) if exists(self.time_mlp) else None h = [] # downsample for block1, block2, attn, downsample in self.downs: x = block1(x, t) x = block2(x, t) x = attn(x) h.append(x) x = downsample(x) # bottleneck x = self.mid_block1(x, t) x = self.mid_attn(x) x = self.mid_block2(x, t) # upsample for block1, block2, attn, upsample in self.ups: x = torch.cat((x, h.pop()), dim=1) x = block1(x, t) x = block2(x, t) x = attn(x) x = upsample(x) return self.final_conv(x)3.7 定义前向扩散过程
DDPM中使用linear schedule定义 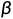 。后续的研究指出使用cosine schedule可能会有更好的效果。
。后续的研究指出使用cosine schedule可能会有更好的效果。
接下来是一些简单的对于 schedule 的定义,从当中选一个使用即可。
def cosine_beta_schedule(timesteps, s=0.008): """ cosine schedule as proposed in https://arxiv.org/abs/2102.09672 """ steps = timesteps + 1 x = torch.linspace(0, timesteps, steps) alphas_cumprod = torch.cos(((x / timesteps) + s) / (1 + s) * torch.pi * 0.5) ** 2 alphas_cumprod = alphas_cumprod / alphas_cumprod[0] betas = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1]) return torch.clip(betas, 0.0001, 0.9999)def linear_beta_schedule(timesteps): beta_start = 0.0001 beta_end = 0.02 return torch.linspace(beta_start, beta_end, timesteps)def quadratic_beta_schedule(timesteps): beta_start = 0.0001 beta_end = 0.02 return torch.linspace(beta_start**0.5, beta_end**0.5, timesteps) ** 2def sigmoid_beta_schedule(timesteps): beta_start = 0.0001 beta_end = 0.02 betas = torch.linspace(-6, 6, timesteps) return torch.sigmoid(betas) * (beta_end - beta_start) + beta_start我们按照DDPM中用第二种的linear,将 T 设置为200,并将每个 t 下的各种参数提前计算好。
timesteps = 200# define beta schedulebetas = linear_beta_schedule(timesteps=timesteps)# define alphas alphas = 1. - betasalphas_cumprod = torch.cumprod(alphas, axis=0)alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)sqrt_recip_alphas = torch.sqrt(1.0 / alphas)# calculations for diffusion q(x_t | x_{t-1}) and otherssqrt_alphas_cumprod = torch.sqrt(alphas_cumprod)sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod)# calculations for posterior q(x_{t-1} | x_t, x_0)posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod)def extract(a, t, x_shape): batch_size = t.shape[0] out = a.gather(-1, t.cpu()) return out.reshape(batch_size, *((1,) * (len(x_shape) - 1))).to(t.device)我们用一个实例来说明前向加噪过程。
from PIL import Imageimport requestsurl = 'http://images.cocodataset.org/val2017/000000039769.jpg'image = Image.open(requests.get(url, stream=True).raw)image
from torchvision.transforms import Compose, ToTensor, Lambda, ToPILImage, CenterCrop, Resizeimage_size = 128transform = Compose([ Resize(image_size), CenterCrop(image_size), ToTensor(), # turn into Numpy array of shape HWC, divide by 255 Lambda(lambda t: (t * 2) - 1),])x_start = transform(image).unsqueeze(0)x_start.shape # 输出的结果是 torch.Size([1, 3, 128, 128])import numpy as npreverse_transform = Compose([ Lambda(lambda t: (t + 1) / 2), Lambda(lambda t: t.permute(1, 2, 0)), # CHW to HWC Lambda(lambda t: t * 255.), Lambda(lambda t: t.numpy().astype(np.uint8)), ToPILImage(),])准备齐全,接下来就可以定义正向扩散过程了。
# forward diffusion (using the nice property)def q_sample(x_start, t, noise=None): if noise is None: noise = torch.randn_like(x_start) sqrt_alphas_cumprod_t = extract(sqrt_alphas_cumprod, t, x_start.shape) sqrt_one_minus_alphas_cumprod_t = extract( sqrt_one_minus_alphas_cumprod, t, x_start.shape ) return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noisedef get_noisy_image(x_start, t): # add noise x_noisy = q_sample(x_start, t=t) # turn back into PIL image noisy_image = reverse_transform(x_noisy.squeeze()) return noisy_image可视化一下多个不同t的生成结果。
import matplotlib.pyplot as plt# use seed for reproducabilitytorch.manual_seed(0)# source: https://pytorch.org/vision/stable/auto_examples/plot_transforms.html#sphx-glr-auto-examples-plot-transforms-pydef plot(imgs, with_orig=False, row_title=None, **imshow_kwargs): if not isinstance(imgs[0], list): # Make a 2d grid even if there's just 1 row imgs = [imgs] num_rows = len(imgs) num_cols = len(imgs[0]) + with_orig fig, axs = plt.subplots(figsize=(200,200), nrows=num_rows, ncols=num_cols, squeeze=False) for row_idx, row in enumerate(imgs): row = [image] + row if with_orig else row for col_idx, img in enumerate(row): ax = axs[row_idx, col_idx] ax.imshow(np.asarray(img), **imshow_kwargs) ax.set(xticklabels=[], yticklabels=[], xticks=[], yticks=[]) if with_orig: axs[0, 0].set(title='Original image') axs[0, 0].title.set_size(8) if row_title is not None: for row_idx in range(num_rows): axs[row_idx, 0].set(ylabel=row_title[row_idx]) plt.tight_layout()plot([get_noisy_image(x_start, torch.tensor([t])) for t in [0, 50, 100, 150, 199]])
3.8 定义损失函数
def p_losses(denoise_model, x_start, t, noise=None, loss_type="l1"): # 先采样噪声 if noise is None: noise = torch.randn_like(x_start) # 用采样得到的噪声去加噪图片 x_noisy = q_sample(x_start=x_start, t=t, noise=noise) predicted_noise = denoise_model(x_noisy, t) # 根据加噪了的图片去预测采样的噪声 if loss_type == 'l1': loss = F.l1_loss(noise, predicted_noise) elif loss_type == 'l2': loss = F.mse_loss(noise, predicted_noise) elif loss_type == "huber": loss = F.smooth_l1_loss(noise, predicted_noise) else: raise NotImplementedError() return loss3.9 定义数据集 PyTorch Dataset 和 DataLoader
我们使用mnist数据集构造了一个 DataLoader,每个batch由128张 normalize 过的 image 组成。
from datasets import load_dataset# load dataset from the hubdataset = load_dataset("fashion_mnist")image_size = 28channels = 1batch_size = 128from torchvision import transformsfrom torch.utils.data import DataLoadertransform = Compose([ transforms.RandomHorizontalFlip(), transforms.ToTensor(), transforms.Lambda(lambda t: (t * 2) - 1)])def transforms(examples): examples["pixel_values"] = [transform(image.convert("L")) for image in examples["image"]] del examples["image"] return examplestransformed_dataset = dataset.with_transform(transforms).remove_columns("label")dataloader = DataLoader(transformed_dataset["train"], batch_size=batch_size, shuffle=True)batch = next(iter(dataloader))print(batch.keys()) # dict_keys(['pixel_values'])3.10 采样
采样过程发生在反向去噪时。对于一张纯噪声,扩散模型一步步地去除噪声最终得到真实图片,采样事实上就是定义的去除噪声这一行为。 观察采样算法中第四行, t−1 步的图片是由 t 步的图片减去一个噪声得到的,只不过这个噪声是由网络拟合出来,并且 rescale 过的而已。 这里要注意第四行式子的最后一项,采样时每一步也都会加上一个从正态分布采样的纯噪声。理想情况下,最终我们会得到一张看起来像是从真实数据分布中采样得到的图片。

@torch.no_grad()def p_sample(model, x, t, t_index): betas_t = extract(betas, t, x.shape) sqrt_one_minus_alphas_cumprod_t = extract( sqrt_one_minus_alphas_cumprod, t, x.shape ) sqrt_recip_alphas_t = extract(sqrt_recip_alphas, t, x.shape) # Equation 11 in the paper # Use our model (noise predictor) to predict the mean model_mean = sqrt_recip_alphas_t * ( x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t ) if t_index == 0: return model_mean else: posterior_variance_t = extract(posterior_variance, t, x.shape) noise = torch.randn_like(x) # Algorithm 2 line 4: return model_mean + torch.sqrt(posterior_variance_t) * noise # Algorithm 2 (including returning all images)@torch.no_grad()def p_sample_loop(model, shape): device = next(model.parameters()).device b = shape[0] # start from pure noise (for each example in the batch) img = torch.randn(shape, device=device) imgs = [] for i in tqdm(reversed(range(0, timesteps)), desc='sampling loop time step', total=timesteps): img = p_sample(model, img, torch.full((b,), i, device=device, dtype=torch.long), i) imgs.append(img.cpu().numpy()) return imgs@torch.no_grad()def sample(model, image_size, batch_size=16, channels=3): return p_sample_loop(model, shape=(batch_size, channels, image_size, image_size))3.11 训练

先定义一些辅助生成图片的函数。
from pathlib import Pathdef num_to_groups(num, divisor): groups = num // divisor remainder = num % divisor arr = [divisor] * groups if remainder > 0: arr.append(remainder) return arrresults_folder = Path("./results")results_folder.mkdir(exist_ok = True)save_and_sample_every = 1000接下来实例化模型。
from torch.optim import Adamdevice = "cuda" if torch.cuda.is_available() else "cpu"model = Unet( dim=image_size, channels=channels, dim_mults=(1, 2, 4,))model.to(device)optimizer = Adam(model.parameters(), lr=1e-3)开始训练!
from torchvision.utils import save_imageepochs = 6for epoch in range(epochs): for step, batch in enumerate(dataloader): optimizer.zero_grad() batch_size = batch["pixel_values"].shape[0] batch = batch["pixel_values"].to(device) # Algorithm 1 line 3: sample t uniformally for every example in the batch t = torch.randint(0, timesteps, (batch_size,), device=device).long() loss = p_losses(model, batch, t, loss_type="huber") if step % 100 == 0: print("Loss:", loss.item()) loss.backward() optimizer.step() # save generated images if step != 0 and step % save_and_sample_every == 0: milestone = step // save_and_sample_every batches = num_to_groups(4, batch_size) all_images_list = list(map(lambda n: sample(model, batch_size=n, channels=channels), batches)) all_images = torch.cat(all_images_list, dim=0) all_images = (all_images + 1) * 0.5 save_image(all_images, str(results_folder / f'sample-{milestone}.png'), nrow = 6)Inference:
# sample 64 imagessamples = sample(model, image_size=image_size, batch_size=64, channels=channels)# show a random onerandom_index = 5plt.imshow(samples[-1][random_index].reshape(image_size, image_size, channels), cmap="gray")
import matplotlib.animation as animationrandom_index = 53fig = plt.figure()ims = []for i in range(timesteps): im = plt.imshow(samples[i][random_index].reshape(image_size, image_size, channels), cmap="gray", animated=True) ims.append([im])animate = animation.ArtistAnimation(fig, ims, interval=50, blit=True, repeat_delay=1000)animate.save('diffusion.gif')plt.show()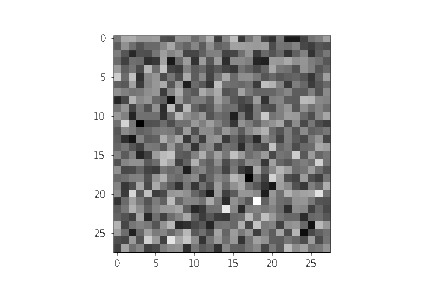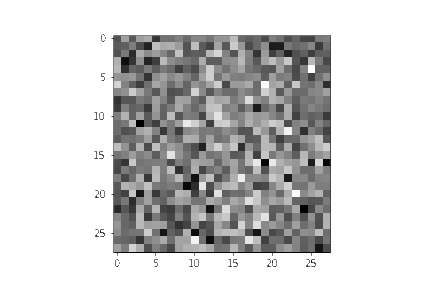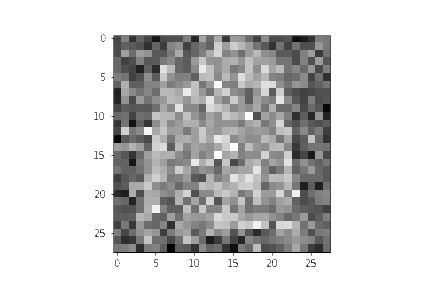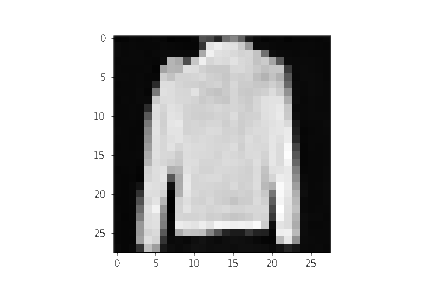
4. 参考文献
原理+代码:Diffusion Model 直观理解
The Annotated Diffusion Model
【diffusion】扩散模型详解!理论+代码