Typescript 是 Javascript 的超集。Typescript 为 Javascript 增加类型能力，主要为了避免 JS 弱类型下产生的各种有意无意的问题。Typescript 的出现大大改善了开发体验，增强了代码的可维护性和稳定性，如今已被越来越多的大型前端项目选用。

【文末送书】：评论区抽一位朋友送出书籍《有趣的矩阵：看得懂又好看的线性代数》一本，包邮到家

本系列将使用TypeScript实战算法，题目全部来源于力扣题库：《剑指 Offer（第 2 版）》，本章节包括的题目有：

题目	难度
数组中重复的数字	简单
二维数组中的查找	中等
替换空格	简单
从尾到头打印链表	简单
重建二叉树	中等
用两个栈实现队列	简单
斐波拉契数列	简单
青蛙跳台阶问题	简单
旋转数组的最小数字	简单
矩阵中的路径	中等

一、数组中重复的数字

1.1、题目描述

找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

示例 1：

输入： [2, 3, 1, 0, 2, 5, 3] 输出：2 或 3

1.2、题解

①：哈希表解法
时间复杂度为O（n），空间复杂度为O（n）
本题可以采用哈希表来解很简单storeSet.has(nums[i])用于判断哈希表内是否有这个数。
不熟悉TypeScript哈希表的朋友可以看这一篇：TypeScript算法题实战——哈希表篇

function findRepeatNumber(nums: number[]): number {    let storeSet: Set<number> = new Set();    for(let i:number = 0; i < nums.length; i++){        if(storeSet.has(nums[i])){            return nums[i];        }        else{            storeSet.add(nums[i]);        }    }    return -1;};

②：原地哈希解法（鸽巢原理/抽屉原理）
时间复杂度O（n），空间复杂度O（1）
这一步的原理简单来讲就是边做边交换让其排序到正确的位置，遍历数组，比如遍历第一个数为3，那么把第一个数和第三个数进行交换，如果有重复的，在交换的时候你会发现要交换的数与本数相同，然后return出数字就好。

function findRepeatNumber(nums: number[]): number {    for(let i:number = 0; i < nums.length; i++){        while(nums[i] != i){            if(nums[nums[i]] == nums[i])                return nums[i];            let tmp = nums[nums[i]];            nums[nums[i]] = nums[i];            nums[i] = tmp;        }    }    return -1;};

二、二维数组中的查找

2.1、题目描述

在一个 n * m 的二维数组中，每一行都按照从左到右 非递减 的顺序排序，每一列都按照从上到下 非递减 的顺序排序。请完成一个高效的函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

示例:

现有矩阵 matrix 如下：

[ [1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30] ]
给定 target = 5，返回 true。
给定 target = 20，返回 false。

2.2、题解

站在右上角看。这个矩阵其实就像是一个Binary Search Tree（二叉搜索树），从右上开始算，target大于该数就向下，小于该数就向左。
时间复杂度O（n），空间复杂度O(1)

function findNumberIn2DArray(matrix: number[][], target: number): boolean {    if(matrix.length == 0)        return false;    if(matrix[0].length == 0)        return false;    let x = 0;    let y = matrix[0].length - 1;    while(x < matrix.length && y > -1){        if(matrix[x][y] == target)            return true;        if(matrix[x][y] < target){            x++;            continue;        }        if(matrix[x][y] > target){            y--;            continue;        }    }    return false;};

三、替换空格

3.1、题目描述

请实现一个函数，把字符串 s 中的每个空格替换成"%20"。

示例 1：

输入：s = “We are happy.”
输出：“We%20are%20happy.”

3.2、题解

①、遍历
遇到“ ”在结尾加“%20”，遇到其他直接加
时间复杂度：O(n)，空间复杂度O（n）

function replaceSpace(s: string): string {    let res:string = "";    for(let i of s){        if(i===" ")             res+="%20";        else             res+=i;    }    return res;};

②、分割
首先使用split以空格为标识将s分割为数组，然后使用join把他们用“%20”连接起来。
时间复杂度：O（n） 空间复杂度O（n）

function replaceSpace(s: string): string {    let arr: string[] = s.split(" ");    return arr.join("%20");};

四、 从尾到头打印链表

4.1、题目描述

输入一个链表的头节点，从尾到头反过来返回每个节点的值（用数组返回）。

示例 1：

输入：head = [1,3,2] 输出：[2,3,1]

4.2、题解

①：迭代
遍历一次链表，使用数组记录值，然后再使用双指针倒转一次数组。

function reversePrint(head: ListNode | null): number[] {    let res:number[] = [];    let i = 0;    while(head != null){        res[i] = head.val;        head = head.next;        i++;    }    for (let i = 0, j = res.length - 1; i < j; i++, j--) {        const c = res[i]        res[i] = res[j]        res[j] = c    }    return res;};

②：递归
使用dfs，将最深层的最先放入数组中，每次先将当前节点的 next 指针进行递归处理，然后再将当前节点值加入数组，即可实现「从后往前」的顺序添加。

function reversePrint(head: ListNode | null): number[] {    const ans: number[] = new Array<number>()    function dfs(head: ListNode | null){        if(head == null)            return;        dfs(head.next);        ans.push(head.val);    }    dfs(head)    return ans};

五、重建二叉树

5.1、题目描述

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

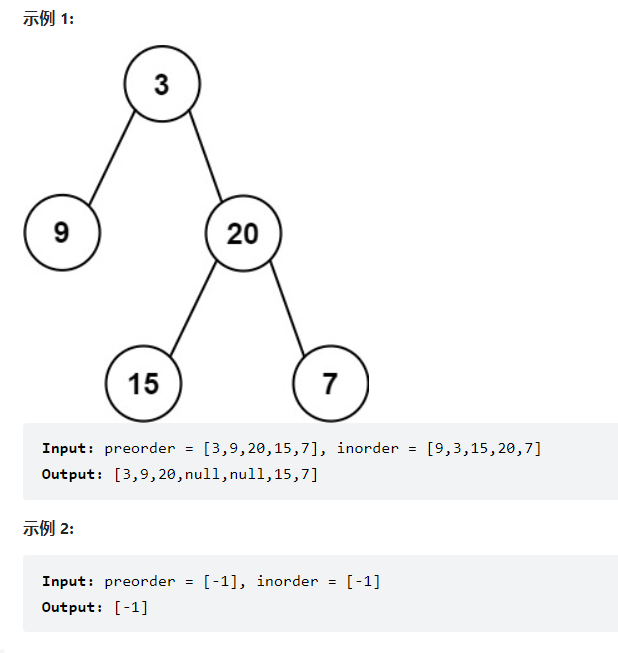
5.2、题解

本题是经典已知前序和中序，重建二叉树：

二叉树前序遍历的顺序为，先遍历根节点，随后递归地遍历左子树，最后递归遍历右子树。二叉树中序遍历的顺序为：先递归地遍历左子树，随后遍历根节点，最后递归遍历右子树。

前序遍历的第一个节点定然是当前树的根节点，构建树节点，拿 root 把中序遍历的数组劈开，左边为左子树，右边为右子树，递归操作就可以了。

function buildTree(preorder: number[], inorder: number[]): TreeNode | null {    if(preorder.length == 0|| inorder.length ==0 )        return null;    let root: TreeNode = new TreeNode(preorder[0]);    const currIndex = inorder.indexOf(preorder[0]);    preorder.shift();    root.left = buildTree(preorder, inorder.slice(0, currIndex));    root.right = buildTree(preorder, inorder.slice(currIndex + 1));    return root;};

六、用两个栈实现队列

6.1、题目描述

用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

示例 1：

输入： [“CQueue”,“appendTail”,“deleteHead”,“deleteHead”,“deleteHead”]
[[],[3],[],[],[]] 输出：[null,null,3,-1,-1]

示例 2：

输入：
[“CQueue”,“deleteHead”,“appendTail”,“appendTail”,“deleteHead”,“deleteHead”]
[[],[],[5],[2],[],[]] 输出：[null,-1,null,null,5,2]

6.2、题解

这题的题目已经在题目告诉我们，也就是要用两个栈构造一个队列，栈是先进后出，队列先进先出。那么构造两个栈，一个是输入栈一个是输出栈，在输入时，直接往输入栈中压栈就好了，在输出的时候，首先判断输出栈中有无元素，有则直接弹出，没有的话将输入栈的元素挨个弹出再压入输出栈中，做完这一步后，再弹出输出栈的元素就好。

class CQueue {    instack: number[];    outstack: number[];    constructor() {        this.instack = [];        this.outstack = [];    }    appendTail(value: number): void {        this.instack.push(value);    }    deleteHead(): number {        if(this.outstack.length != 0)            return this.outstack.pop();        while(this.instack.length != 0){            this.outstack.push(this.instack.pop());        }        if(this.outstack.length != 0)            return this.outstack.pop();        return -1;    }}

七、I. 斐波那契数列

7.1、题目描述

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

7.2、题解

这题若直接用简单递归肯定会超时，下面使用动态规划或者记忆递归来做。

①、动态规划
时间复杂度：O（n），空间复杂度：O（n）

function fib(n: number): number {    let fidArray = [];    fidArray[0] = 0;    fidArray[1] = 1;    for(let i = 2; i < n + 1; i++){        fidArray[i] = (fidArray[i - 1] + fidArray[i -2]) % 1000000007;     }    return fidArray[n];};

②、记忆递归法
时间复杂度：O（n） 空间复杂度O（n）
使用一个Map<number, number>()记录已经算过的值，一key：value的方式存储，memory.has(n)用于判断是否算过key为n的值，memory.get(n)用于返回key为n的值。

function fib(n: number): number {    let memory = new Map<number, number>();    function fibMemory(n:number, memory:Map<number, number>){        if(n == 1) return 1;        if(n == 0) return 0;        if(memory.has(n)){        return memory.get(n);        }        let res = (fibMemory(n - 1, memory) + fibMemory(n - 2, memory)) %1000000007;        memory.set(n, res);        return res;    }    return fibMemory(n, memory)};

八、II. 青蛙跳台阶问题

8.1、题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

8.2、题解

同斐波拉契数列，只不过初始fidArray[0] = 1;fidArray[1] = 1;，这样fidArray[2] = fidArray[0] + fidArray[1] = 2；

①、动态规划
时间复杂度O（n） 空间复杂度O（n）

function numWays(n: number): number {    let fidArray = [];    fidArray[0] = 1;    fidArray[1] = 1;    for(let i = 2; i < n + 1; i++){        fidArray[i] = (fidArray[i - 1] + fidArray[i -2]) % 1000000007;     }    return fidArray[n];};

②、记忆递归
时间复杂度O（n） 空间复杂度O（n）

function numWays(n: number): number {    let memory = new Map<number, number>();    function fibMemory(n:number, memory:Map<number, number>){        if(n == 1) return 1;        if(n == 0) return 0;        if(memory.has(n)){        return memory.get(n);        }        let res = (fibMemory(n - 1, memory) + fibMemory(n - 2, memory)) %1000000007;        memory.set(n, res);        return res;    }    return fibMemory(n, memory)};

九、 旋转数组的最小数字

9.1、题目描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

给你一个可能存在 重复 元素值的数组 numbers ，它原来是一个升序排列的数组，并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转，该数组的最小值为 1。

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

示例 1：
输入：numbers = [3,4,5,1,2]
输出：1
示例 2：
输入：numbers = [2,2,2,0,1]
输出：0

9.2、题解

无论数组旋转过多少次，他们内部的链条是不会变的，依然还是一个环形，只是说这个环的开头变了，我们可以使用双指针进行二分法来解

function minArray(numbers: number[]): number {    let left = 0;    let right = numbers.length - 1;    while(left != right){        let mid = left +Math.floor((right - left) / 2);        if(numbers[mid] > numbers[right]){            left = mid + 1;        }        else if(numbers[mid] < numbers[right]){            right = mid;        }        else{            right = right - 1;        }    }    return numbers[left];};

十、矩阵中的路径

10.1、题目描述

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

例如，在下面的 3×4 的矩阵中包含单词 “ABCCED”（单词中的字母已标出）。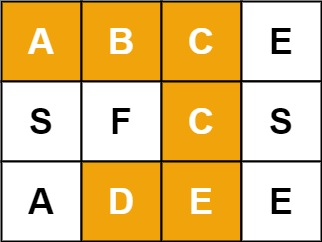

示例 1：

输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]],
word = “ABCCED” 输出：true
示例 2：

输入：board = [[“a”,“b”],[“c”,“d”]], word = “abcd” 输出：false

10.2、题解

深度优先搜索算法，首先判断是否溢出边界，然后判断是否访问过（这里设置已访问过的元素置为空），然后判断是否等于当前所需字母，最后判断是否满足所需字符串长度。

在判断的时候，同时判断四个方向的情况，并用逻辑或连接他们的结果。

function exist(board: string[][], word: string): boolean {    function dfs(i: number, j: number, index:number): boolean{        if(i < 0 || i >= board.length)            return false;        if(j < 0 || j >= board[i].length)            return false;        if(board[i][j] == ' ')            return false;        if(board[i][j] != word[index])            return false;        if(index == word.length - 1)            return true;                let tempValue = board[i][j];        board[i][j] = ' ';        let res = dfs(i + 1, j, index + 1) || dfs(i -1, j, index + 1) || dfs(i, j + 1, index + 1) || dfs(i, j - 1, index + 1) ;        board[i][j] = tempValue;        return res;    }    for(let i = 0; i < board.length; i++){        for(let j = 0; j < board[i].length; j++){            if(dfs(i, j, 0)) return true;        }    }    return false;};

书籍推荐

京东购买链接：https://item.jd.com/13640773.html

【内容简介】

本书分别从中国古代数学思想、益智游戏、企业管理、计算机科学、博弈论等角度出发，介绍了线性代数和矩阵理论中的相关概念和理论在上述领域的应用。通过阅读本书，读者对线性代数在实际问题中的应用会有更加直观的了解，有助于激发读者对线性代数的学习兴趣和学习热情。

本书分为8章，涵盖的主要内容有线性方程组的计算、益智数字游戏中的矩阵、经营管理中的矩阵、矩阵与图片美化、计算机绘画中的矩阵、矩阵与密码设计、互联网中的矩阵、矩阵与博弈论。

本书内容通俗易懂、生动有趣，特别适合中学生、大学生及各年龄层的数学爱好者作为线性代数入门读物使用。另外，本书也适合作为各类大中专院校的教学参考书使用。

【适合人群】

多次迭代的线性代数硬核教程：理工生自学佳选，线性代数学习好帮手，内容千锤百炼，反复反馈、打磨、迭代，示例来源于生活，激发读者兴趣，降低理解难度。

多图：数缺形时少直观，形少数时难入微，数形结合百般好。经典：内容千锤百炼，在使用中反复反馈、打磨、迭代。实战：示例来源于生活，激发读者兴趣，降低理解难度。硬核：多次迭代的硬核教程，线性代数学习好帮手。

【作者简介】

马婧瑛，博士，宁夏大学副教授，硕士生导师。发表高质量学术论文十余篇，获得宁夏自然科学优秀学术论文一等奖一项（排名第一）、二等奖一项（排名第二）。多年担任宁夏大学线性代数课程讲授工作。

汪文帅，博士，宁夏大学教授，博士生导师。兼任中国数学会理事、第二届中国智能物联系统建模与仿真专业委员会委员。发表高质量学术论文三十余篇，出版专著一部，曾获宁夏回族自治区科技进步二等奖、宁夏哲学社会科学优秀成果二等奖、宁夏回族自治区教学成果二等奖、宝钢优秀教师奖。

【活动介绍】

北京大学出版社，4月“423世界读书日”促销活动安排：
当当活动日期：4.6-4.11，4.18-4.23
京东活动日期： 4.6 一天， 4.17-4.23
活动期间满100减50或者半价5折销售
欢迎大家关注参与423读书日北大社促销活动