先看几条定义:
1、二叉树是一种每个结点最多只能有两个孩子的树。
2、每一个子集本身又是一棵符合定义的树,叫做根节点的子树。
3、每一棵子树的根叫做根 r 的孩子,而 r 是每一棵子树的根的双亲。
4、具有相同双亲的结点称为兄弟。
5、树中结点所在的最大层次称为树的深度(或高度)。
6、树的访问顺序一般有先序、中序、后序、层次四种。
先序:根结点->左子树->右子树
中序:左子树->根结点->右子树
后序:左子树->右子树->根结点
层次:逐层访问,从左到右
这里我采用的是先序创建。用来测试程序的二叉树为ABD#G###CE##F##,后续插入操作插入的二叉树为HJK####(基于先序顺序)。如图所示:
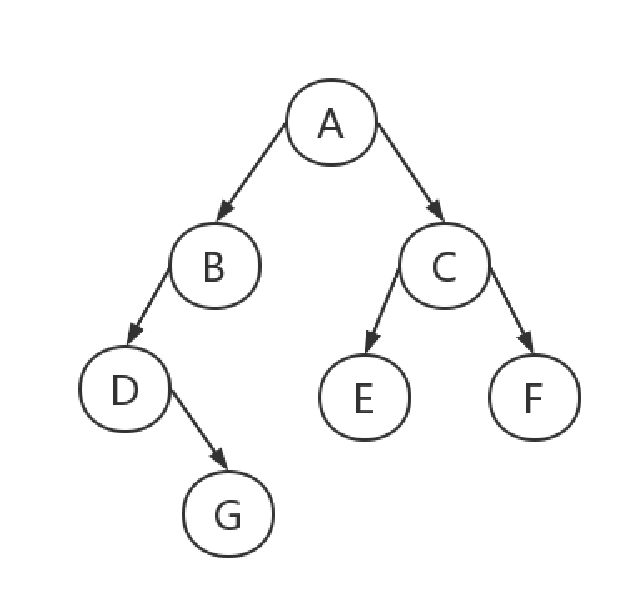
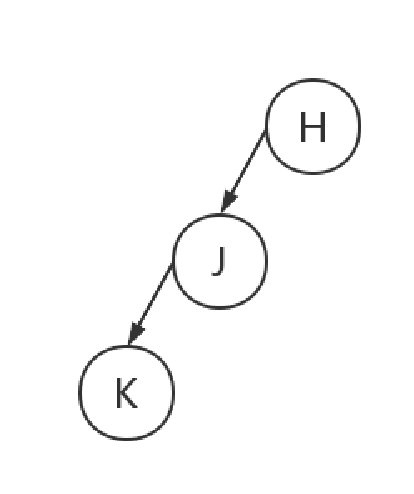
基本数据结构:
typedef struct BiTNode {char data; //数据struct BiTNode* lchild; //左孩子struct BiTNode* rchild; //右孩子}BiTNode, * BiTree;1、初始化
void Init_Tree(BiTree& T) //1、初始化{T = (BiTNode*)malloc(sizeof(BiTNode));T->data = '#';T->lchild = NULL;T->rchild = NULL;}2、销毁(基于后序顺序)
void Destroy_Tree(BiTree& T) //2、销毁(基于后序顺序){if (T) {Destroy_Tree(T->lchild); //销毁左子树Destroy_Tree(T->rchild); //销毁右子树free(T); //释放结点}}3、创建(基于先序顺序)
void Create_Tree(BiTree& T) //3、创建(基于先序顺序){char c;cin >> c;if (c == '#') { // # 代表空指针T = NULL;}else { //创建根节点T = (BiTNode*)malloc(sizeof(BiTNode));T->data = c;Create_Tree(T->lchild); //先序创建左分支Create_Tree(T->rchild); //先序创建右分支}}4、清空(释放根之外的空间)
void Clear_Tree(BiTree& T) //4、清空(释放根之外的空间){Destroy_Tree(T->lchild); //销毁T的左子树Destroy_Tree(T->rchild); //销毁T的右子树T = NULL;}5、判段是否为空
bool Empty_Tree(BiTree T) //5、判空{if (T == NULL || T->data == '#') { return true;}else {return false;}}6、求深度
int Depth_Tree(BiTree T) //6、返回深度{int leftdepth, rightdepth;if (T == NULL) {return 0; //到空时,返回0}else {leftdepth = Depth_Tree(T->lchild); //求左子树深度rightdepth = Depth_Tree(T->rchild); //求右子树深度return max(leftdepth + 1, rightdepth + 1); //最终取较大深度}}7、返回根的元素值
8、返回p指针指向的结点值
char Root_Tree(BiTree T) //7、返回根的元素值{if (T != NULL) { //树不为空return T->data;}else {return '#';}}char Value_Tree(BiTree T, BiTree p) //8、返回p指针指向的结点值{if (T == NULL || p == NULL) {return '#';}else {return p->data;}}9、若p非T的根节点,则返回其双亲指针,否则返回NULL
10、返回p的左孩子指针,若没有返回NULL
11、返回p的右孩子指针,若没有返回NULL
12、返回p的左兄弟指针,若没有返回NULL
13、返回p的右兄弟指针,若没有返回NULL
BiTree Parent_Tree(BiTree T, BiTree p) //9、若p非T的根节点,则返回其双亲指针,否则返回NULL{BiTree q = NULL;if (T == NULL || p == T) { //如果p等于根节点,返回NULLreturn NULL;}else {if (T->lchild == p || T->rchild == p) { //T是p的双亲,返回Treturn T;}q = Parent_Tree(T->lchild, p); //在左分支中查找if (q == NULL) { //左分支中没有找到,查找右分支q = Parent_Tree(T->rchild, p);return q;}return q;}}BiTree LeftChild_Tree(BiTree T, BiTree p) //10、返回p的左孩子指针,若没有返回NULL{if (T != NULL && p != NULL) {return p->lchild;}else {return NULL;}}BiTree RightChild_Tree(BiTree T, BiTree p) //11、返回p的右孩子指针,若没有返回NULL{if (T != NULL && p != NULL) {return p->rchild;}else {return NULL;}}BiTree LeftBrother_Tree(BiTree T, BiTree p) //12、返回p的左兄弟指针,若没有返回NULL{if (T == NULL) {return NULL;}else {BiTree q = Parent_Tree(T, p); //先找到双亲结点if (q != NULL && q->lchild != p) {return q->lchild;}else {return NULL;}}}BiTree RightBrother_Tree(BiTree T, BiTree p) //13、返回p的右兄弟指针,若没有返回NULL{if (T == NULL) {return NULL;}else {BiTree q = Parent_Tree(T, p);if (q != NULL && q->rchild != p) {return q->rchild;}else {return NULL;}}}14、先序遍历并打印
15、中序遍历并打印
16、后序遍历并打印
void PrePrint_Tree(BiTree T) //14、先序遍历并打印{if (T != NULL) {cout << T->data; //访问根节点PrePrint_Tree(T->lchild); //先序遍历左子树PrePrint_Tree(T->rchild); //先序遍历右子树}}void InPrint_Tree(BiTree T) //15、中序遍历并打印{if (T != NULL) {InPrint_Tree(T->lchild); //中序遍历左子树cout << T->data; //访问根节点InPrint_Tree(T->rchild); //中序遍历右子树}}void PostPrint_Tree(BiTree T) //16、后序遍历并打印{if (T != NULL) {PostPrint_Tree(T->lchild); //后序遍历左子树PostPrint_Tree(T->rchild); //后序遍历右子树cout << T->data; //访问根节点}}17、层次遍历并打印
void LevelPrint_Tree(BiTree T) //17、层次遍历并打印{BiTree p;queue<BiTree>qu; //定义队列,存放二叉树结点指针(这里使用了STL的queue类型)qu.push(T); //根节点入队while (!qu.empty()) {p = qu.front();cout << p->data; //访问队首结点qu.pop(); //队首结点出队if (p->lchild != NULL) {qu.push(p->lchild); //若结点有左孩子,则左孩子入队}if (p->rchild != NULL) {qu.push(p->rchild); //若结点有右孩子,则左孩子入队}}}18、将p结点元素赋值为c
19、插入(插入的为非空二叉树,且右子树为空)
void Assign_Tree(BiTree& T, BiTree p, char c) //18、将p结点元素赋值为c{if (T == NULL || p == NULL) {return;}else {p->data = c;}}void Insert_Tree(BiTree& T, BiTree p, int LR, BiTree c) //19、插入(c为非空二叉树,且右子树为空){if (T == NULL || p == NULL || c == NULL) {return;}else {if (LR == 0) { //LR为0,则c作为p的左子树;为1,则c作为p的右子树c->rchild = p->lchild; //把原来的左子树连接在c的右子树上p->lchild = c;}else {c->rchild = p->rchild; //把原来的右子树连接在c的右子树上p->rchild = c;}}}20、删除子树
void Delete_Tree(BiTree& T, BiTree p, int LR) //20、删除子树{if (T == NULL || p == NULL) {return;}if (LR == 0) { //删除p的左子树Destroy_Tree(p->lchild);p->lchild = NULL;}else { //删除p的右子树Destroy_Tree(p->rchild);p->rchild = NULL;}}21、先序查找指定元素值的结点
BiTree Find_Tree(BiTree T, char c) //21、先序查找指定元素值的二叉树结点{BiTree p = NULL;if (T == NULL) {return NULL;}else if (T->data == c) { //访问的当前结点值等于c,返回当前指针,查找结束return T;}else {p = Find_Tree(T->lchild, c); //在左分支中先序查找if (p == NULL) {p = Find_Tree(T->rchild, c); //左分支中未找到,继续先序查找右分支return p; //返回右分支查找结果}return p; //左分支中找到,返回当前指针,查找结束}}主函数(用于测试):
int main(){BiTree T;Init_Tree(T); //1、初始化bool t = Empty_Tree(T); //5、判空if (t) {cout << "二叉树为空" << endl;}else {cout << "二叉树非空" << endl;}cout << "按先序顺序输入元素:";Create_Tree(T); //3、创建int d = Depth_Tree(T); //6、返回深度cout << "二叉树的深度:" << d << endl;char c = Root_Tree(T); //7、返回根的元素值cout << "根的元素值为:" << c << endl;BiTree p, q; //p为检验程序时使用,可随意更改p的指向cout << "请设置p指针指向的元素:";cin >> c;p = Find_Tree(T, c); //21、先序查找指定元素值的二叉树结点c = Value_Tree(T, p); //8、返回p指针指向的结点值cout << "p指向的结点值:" << c << endl;q = Parent_Tree(T, p); //9、若p非T的根节点,则返回其双亲指针,否则返回NULLcout << "p的双亲指针q指向的元素:" << Value_Tree(T, q) << endl;q = LeftChild_Tree(T, p); //10、返回p的左孩子指针,若没有返回NULLcout << "p的左孩子指针q指向的元素:" << Value_Tree(T, q) << endl;q = RightChild_Tree(T, p); //11、返回p的右孩子指针,若没有返回NULLcout << "p的右孩子指针q指向的元素:" << Value_Tree(T, q) << endl;q = LeftBrother_Tree(T, p); //12、返回p的左兄弟指针,若没有返回NULLcout << "p的左兄弟指针q指向的元素:" << Value_Tree(T, q) << endl;q = RightBrother_Tree(T, p); //13、返回p的右兄弟指针,若没有返回NULLcout << "p的右兄弟指针q指向的元素:" << Value_Tree(T, q) << endl;cout << "先序遍历二叉树:";PrePrint_Tree(T); //14、先序遍历并打印cout << endl;cout << "中序遍历二叉树:";InPrint_Tree(T); //15、中序遍历并打印cout << endl;cout << "后序遍历二叉树:";PostPrint_Tree(T); //16、后序遍历并打印cout << endl;cout << "层次遍历二叉树:";LevelPrint_Tree(T); //17、层次遍历并打印cout << endl;cout << "想要更改的元素值:";cin >> c;q = Find_Tree(T, c); //21、先序查找指定元素值的二叉树结点cout << "更改后的元素值:";cin >> c;Assign_Tree(T, q, c); //18、将p结点元素赋值为ccout << "先序遍历二叉树:";PrePrint_Tree(T); //14、先序遍历并打印cout << endl;BiTree S; //另创建一个根节点右子树为空的二叉树,作为插入的样本Init_Tree(S); //1、初始化cout << "按先序顺序输入要插入的二叉树(根节点右子树为空)的元素:";Create_Tree(S); //3、创建int LR;cout << "请选择要插入的部位(0.p的左子树 1.p的右子树):";cin >> LR;Insert_Tree(T, p, LR, S); //19、插入(S为非空二叉树,且右子树为空)cout << "先序遍历二叉树:";PrePrint_Tree(T); //14、先序遍历并打印cout << endl;cout << "请选择要删除的部位(0.p的左子树 1.p的右子树):";cin >> LR;Delete_Tree(T, p, LR); //20、删除子树cout << "先序遍历二叉树:";PrePrint_Tree(T); //14、先序遍历并打印cout << endl;cout << "二叉树已清空" << endl;Clear_Tree(T); //4、清空(释放根之外的空间)t = Empty_Tree(T); //5、判空if (t) {cout << "二叉树为空" << endl;}else {cout << "二叉树非空" << endl;}Destroy_Tree(T); //2、销毁(基于后序顺序)cout << "二叉树已销毁" << endl;return 0;}下面是全部代码:
# include <iostream># include <stdlib.h># include <queue># define SIZE 256using namespace std;typedef struct BiTNode {char data;struct BiTNode* lchild; //左孩子struct BiTNode* rchild; //右孩子}BiTNode, * BiTree;void Init_Tree(BiTree& T) //1、初始化{T = (BiTNode*)malloc(sizeof(BiTNode));T->data = '#';T->lchild = NULL;T->rchild = NULL;}void Destroy_Tree(BiTree& T) //2、销毁(基于后序顺序){if (T) {Destroy_Tree(T->lchild); //销毁左子树Destroy_Tree(T->rchild); //销毁右子树free(T);}}void Create_Tree(BiTree& T) //3、创建(基于先序顺序){char c;cin >> c;if (c == '#') { // # 代表空指针T = NULL;}else { //创建根节点T = (BiTNode*)malloc(sizeof(BiTNode));T->data = c;Create_Tree(T->lchild); //先序创建左分支Create_Tree(T->rchild); //先序创建右分支}}void Clear_Tree(BiTree& T) //4、清空(释放根之外的空间){Destroy_Tree(T->lchild); //销毁T的左子树Destroy_Tree(T->rchild); //销毁T的右子树T = NULL;}bool Empty_Tree(BiTree T) //5、判空{if (T == NULL || T->data == '#') { return true;}else {return false;}}int Depth_Tree(BiTree T) //6、返回深度{int leftdepth, rightdepth;if (T == NULL) {return 0; //到空时,返回0}else {leftdepth = Depth_Tree(T->lchild); //求左子树深度rightdepth = Depth_Tree(T->rchild); //求右子树深度return max(leftdepth + 1, rightdepth + 1); //最终取较大深度}}char Root_Tree(BiTree T) //7、返回根的元素值{if (T != NULL) { //树不为空return T->data;}else {return '#';}}char Value_Tree(BiTree T, BiTree p) //8、返回p指针指向的结点值{if (T == NULL || p == NULL) {return '#';}else {return p->data;}}BiTree Parent_Tree(BiTree T, BiTree p) //9、若p非T的根节点,则返回其双亲指针,否则返回NULL{BiTree q = NULL;if (T == NULL || p == T) { //如果p等于根节点,返回NULLreturn NULL;}else {if (T->lchild == p || T->rchild == p) { //T是p的双亲,返回Treturn T;}q = Parent_Tree(T->lchild, p); //在左分支中查找if (q == NULL) { //左分支中没有找到,查找右分支q = Parent_Tree(T->rchild, p);return q;}return q;}}BiTree LeftChild_Tree(BiTree T, BiTree p) //10、返回p的左孩子指针,若没有返回NULL{if (T != NULL && p != NULL) {return p->lchild;}else {return NULL;}}BiTree RightChild_Tree(BiTree T, BiTree p) //11、返回p的右孩子指针,若没有返回NULL{if (T != NULL && p != NULL) {return p->rchild;}else {return NULL;}}BiTree LeftBrother_Tree(BiTree T, BiTree p) //12、返回p的左兄弟指针,若没有返回NULL{if (T == NULL) {return NULL;}else {BiTree q = Parent_Tree(T, p); //先找到双亲结点if (q != NULL && q->lchild != p) {return q->lchild;}else {return NULL;}}}BiTree RightBrother_Tree(BiTree T, BiTree p) //13、返回p的右兄弟指针,若没有返回NULL{if (T == NULL) {return NULL;}else {BiTree q = Parent_Tree(T, p);if (q != NULL && q->rchild != p) {return q->rchild;}else {return NULL;}}}void PrePrint_Tree(BiTree T) //14、先序遍历并打印{if (T != NULL) {cout << T->data; //访问根节点PrePrint_Tree(T->lchild); //先序遍历左子树PrePrint_Tree(T->rchild); //先序遍历右子树}}void InPrint_Tree(BiTree T) //15、中序遍历并打印{if (T != NULL) {InPrint_Tree(T->lchild); //中序遍历左子树cout << T->data; //访问根节点InPrint_Tree(T->rchild); //中序遍历右子树}}void PostPrint_Tree(BiTree T) //16、后序遍历并打印{if (T != NULL) {PostPrint_Tree(T->lchild); //后序遍历左子树PostPrint_Tree(T->rchild); //后序遍历右子树cout << T->data; //访问根节点}}void LevelPrint_Tree(BiTree T) //17、层次遍历并打印{BiTree p;queue<BiTree>qu; //定义队列,存放二叉树结点指针(这里使用了STL的queue类型)qu.push(T); //根节点入队while (!qu.empty()) {p = qu.front();cout << p->data; //访问队首结点qu.pop(); //队首结点出队if (p->lchild != NULL) {qu.push(p->lchild); //若结点有左孩子,则左孩子入队}if (p->rchild != NULL) {qu.push(p->rchild); //若结点有右孩子,则左孩子入队}}}void Assign_Tree(BiTree& T, BiTree p, char c) //18、将p结点元素赋值为c{if (T == NULL || p == NULL) {return;}else {p->data = c;}}void Insert_Tree(BiTree& T, BiTree p, int LR, BiTree c) //19、插入(c为非空二叉树,且右子树为空){if (T == NULL || p == NULL || c == NULL) {return;}else {if (LR == 0) { //LR为0,则c作为p的左子树;为1,则c作为p的右子树c->rchild = p->lchild; //把原来的左子树连接在c的右子树上p->lchild = c;}else {c->rchild = p->rchild; //把原来的右子树连接在c的右子树上p->rchild = c;}}}void Delete_Tree(BiTree& T, BiTree p, int LR) //20、删除子树{if (T == NULL || p == NULL) {return;}if (LR == 0) { //删除p的左子树Destroy_Tree(p->lchild);p->lchild = NULL;}else { //删除p的右子树Destroy_Tree(p->rchild);p->rchild = NULL;}}BiTree Find_Tree(BiTree T, char c) //21、先序查找指定元素值的二叉树结点{BiTree p = NULL;if (T == NULL) {return NULL;}else if (T->data == c) { //访问的当前结点值等于c,返回当前指针,查找结束return T;}else {p = Find_Tree(T->lchild, c); //在左分支中先序查找if (p == NULL) {p = Find_Tree(T->rchild, c); //左分支中未找到,继续先序查找右分支return p; //返回右分支查找结果}return p; //左分支中找到,返回当前指针,查找结束}}int main(){BiTree T;Init_Tree(T); //1、初始化bool t = Empty_Tree(T); //5、判空if (t) {cout << "二叉树为空" << endl;}else {cout << "二叉树非空" << endl;}cout << "按先序顺序输入元素:";Create_Tree(T); //3、创建int d = Depth_Tree(T); //6、返回深度cout << "二叉树的深度:" << d << endl;char c = Root_Tree(T); //7、返回根的元素值cout << "根的元素值为:" << c << endl;BiTree p, q; //p为检验程序时使用,可随意更改p的指向cout << "请设置p指针指向的元素:";cin >> c;p = Find_Tree(T, c); //21、先序查找指定元素值的二叉树结点c = Value_Tree(T, p); //8、返回p指针指向的结点值cout << "p指向的结点值:" << c << endl;q = Parent_Tree(T, p); //9、若p非T的根节点,则返回其双亲指针,否则返回NULLcout << "p的双亲指针q指向的元素:" << Value_Tree(T, q) << endl;q = LeftChild_Tree(T, p); //10、返回p的左孩子指针,若没有返回NULLcout << "p的左孩子指针q指向的元素:" << Value_Tree(T, q) << endl;q = RightChild_Tree(T, p); //11、返回p的右孩子指针,若没有返回NULLcout << "p的右孩子指针q指向的元素:" << Value_Tree(T, q) << endl;q = LeftBrother_Tree(T, p); //12、返回p的左兄弟指针,若没有返回NULLcout << "p的左兄弟指针q指向的元素:" << Value_Tree(T, q) << endl;q = RightBrother_Tree(T, p); //13、返回p的右兄弟指针,若没有返回NULLcout << "p的右兄弟指针q指向的元素:" << Value_Tree(T, q) << endl;cout << "先序遍历二叉树:";PrePrint_Tree(T); //14、先序遍历并打印cout << endl;cout << "中序遍历二叉树:";InPrint_Tree(T); //15、中序遍历并打印cout << endl;cout << "后序遍历二叉树:";PostPrint_Tree(T); //16、后序遍历并打印cout << endl;cout << "层次遍历二叉树:";LevelPrint_Tree(T); //17、层次遍历并打印cout << endl;cout << "想要更改的元素值:";cin >> c;q = Find_Tree(T, c); //21、先序查找指定元素值的二叉树结点cout << "更改后的元素值:";cin >> c;Assign_Tree(T, q, c); //18、将p结点元素赋值为ccout << "先序遍历二叉树:";PrePrint_Tree(T); //14、先序遍历并打印cout << endl;BiTree S; //另创建一个根节点右子树为空的二叉树,作为插入的样本Init_Tree(S); //1、初始化cout << "按先序顺序输入要插入的二叉树(根节点右子树为空)的元素:";Create_Tree(S); //3、创建int LR;cout << "请选择要插入的部位(0.p的左子树 1.p的右子树):";cin >> LR;Insert_Tree(T, p, LR, S); //19、插入(S为非空二叉树,且右子树为空)cout << "先序遍历二叉树:";PrePrint_Tree(T); //14、先序遍历并打印cout << endl;cout << "请选择要删除的部位(0.p的左子树 1.p的右子树):";cin >> LR;Delete_Tree(T, p, LR); //20、删除子树cout << "先序遍历二叉树:";PrePrint_Tree(T); //14、先序遍历并打印cout << endl;cout << "二叉树已清空" << endl;Clear_Tree(T); //4、清空(释放根之外的空间)t = Empty_Tree(T); //5、判空if (t) {cout << "二叉树为空" << endl;}else {cout << "二叉树非空" << endl;}Destroy_Tree(T); //2、销毁(基于后序顺序)cout << "二叉树已销毁" << endl;return 0;}测试结果:
二叉树为空按先序顺序输入元素:ABD#G###CE##F##二叉树的深度:4根的元素值为:A请设置p指针指向的元素:Cp指向的结点值:Cp的双亲指针q指向的元素:Ap的左孩子指针q指向的元素:Ep的右孩子指针q指向的元素:Fp的左兄弟指针q指向的元素:Bp的右兄弟指针q指向的元素:#先序遍历二叉树:ABDGCEF中序遍历二叉树:DGBAECF后序遍历二叉树:GDBEFCA层次遍历二叉树:ABCDEFG想要更改的元素值:D更改后的元素值:X先序遍历二叉树:ABXGCEF按先序顺序输入要插入的二叉树(根节点右子树为空)的元素:HJK####请选择要插入的部位(0.p的左子树 1.p的右子树):0先序遍历二叉树:ABXGCHJKEF请选择要删除的部位(0.p的左子树 1.p的右子树):0先序遍历二叉树:ABXGCF二叉树已清空二叉树为空二叉树已销毁以上是我个人的学习成果,很高兴能与大家分享。