Java优先级队列-堆

?1. 二叉树的顺序存储?? 1.1 存储方式??1.2 下标关系? ?2. 堆(heap)??2.1 概念??2.2 操作-向下调整??2.3操作-向上调整??2.4 操作-建堆? ?3. 堆的应用-优先级队列??3.1 概念??3.2 内部原理??3.3 操作-入队列??3.4 操作-出队列（优先级最高）??3.5 返回队首元素（优先级最高）??3.6 代码??3.7 java 中的优先级队列? ?4. 堆的其他应用-TopK 问题?? 5. 面试题??6. 堆的其他应用-堆排序?

大家好，我是晓星航。今天为大家带来的是 Java优先级队列(堆) 的讲解！?

?1. 二叉树的顺序存储?

? 1.1 存储方式?

使用数组保存二叉树结构，方式即将二叉树用层序遍历方式放入数组中。

一般只适合表示完全二叉树，因为非完全二叉树会有空间的浪费。

这种方式的主要用法就是堆的表示。

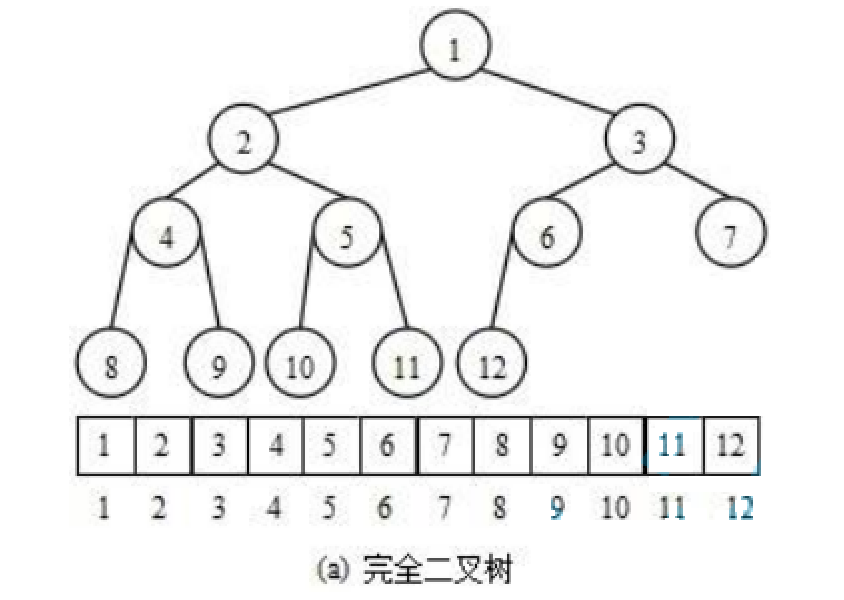
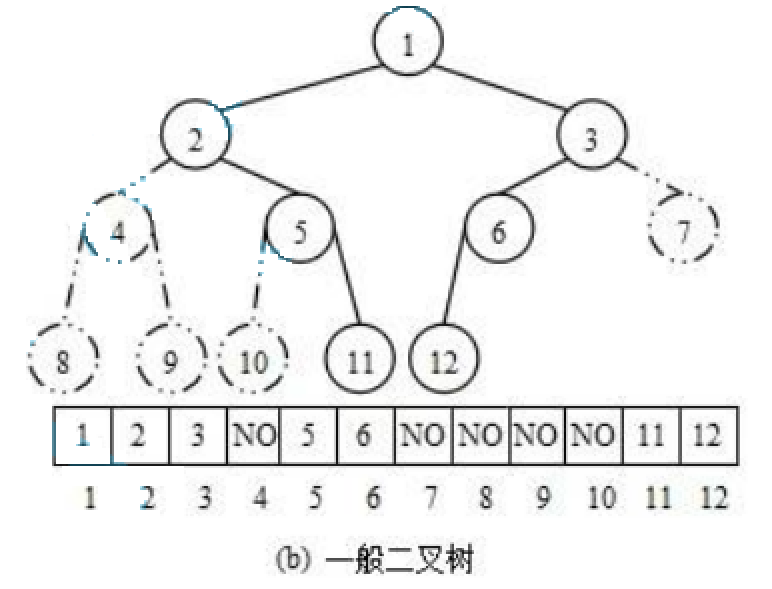
?1.2 下标关系?

已知双亲(parent)的下标，则：

左孩子(left)下标 = 2 * parent + 1;

右孩子(right)下标 = 2 * parent + 2;

已知孩子（不区分左右）(child)下标，则：

双亲(parent)下标 = (child - 1) / 2;

?2. 堆(heap)?

?2.1 概念?

堆逻辑上是一棵完全二叉树堆物理上是保存在数组中满足任意结点的值都大于其子树中结点的值，叫做大堆，或者大根堆，或者最大堆反之，则是小堆，或者小根堆，或者最小堆：每根二叉树的根结点都小于左右孩子节点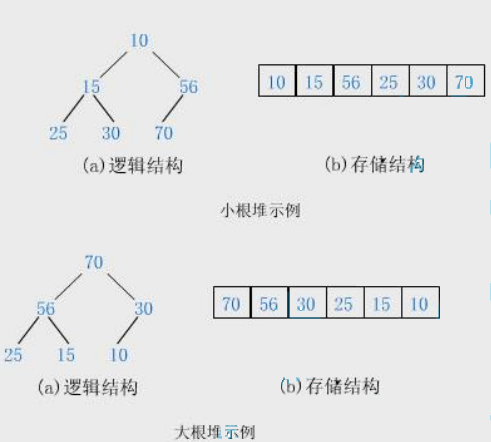堆的基本作用是，快速找集合中的最值

?2.2 操作-向下调整?

**前提：**左右子树必须已经是一个堆，才能调整。

说明：

array 代表存储堆的数组size 代表数组中被视为堆数据的个数index 代表要调整位置的下标left 代表 index 左孩子下标right 代表 index 右孩子下标min 代表 index 的最小值孩子的下标

过程（以小堆为例）：

index 如果已经是叶子结点，则整个调整过程结束

判断 index 位置有没有孩子因为堆是完全二叉树，没有左孩子就一定没有右孩子，所以判断是否有左孩子因为堆的存储结构是数组，所以判断是否有左孩子即判断左孩子下标是否越界，即 left >= size 越界

确定 left 或 right，谁是 index 的最小孩子 min

如果右孩子不存在，则 min = left否则，比较 array[left] 和 array[right] 值得大小，选择小的为 min

比较 array[index] 的值 和 array[min] 的值，如果 array[index] <= array[min]，则满足堆的性质，调整结束

否则，交换 array[index] 和 array[min] 的值

然后因为 min 位置的堆的性质可能被破坏，所以把 min 视作 index，向下重复以上过程

图示：

// 调整前int[] array = { 27,15,19,18,28,34,65,49,25,37 };// 调整后int[] array = { 15,18,19,25,28,34,65,49,27,37 };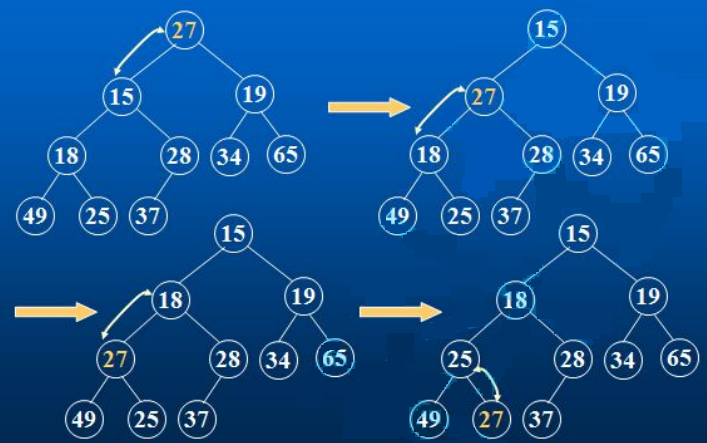

时间复杂度分析：

最坏的情况即图示的情况，从根一路比较到叶子，比较的次数为完全二叉树的高度

即时间复杂度为 O(log(n))

代码：

/** * 向下调整函数的实现 * @param parent 每棵树的根节点 * @param len 每棵树的调整的结束位置 */public void shiftDown(int parent,int len) {    int child = parent * 2 + 1;    //至少有一个左孩子    while (child < len) {        if (child + 1 < len && elem[child] < elem[child + 1]) {            child++;//保证为左右子节点的最大值        }        if (elem[child] > elem[parent]) {            int tmp = elem[child];            elem[child] = elem[parent];            elem[parent] = tmp;            parent = child;            child = parent * 2 + 1;        } else {            break;        }    }}

?2.3操作-向上调整?

同理向上调整的代码为：

/** * 向上调整函数实现 * @param child 添加的子树来进行判断调整 */private void shiftUp(int child) {    int parent = (child - 1) / 2;    while (child > 0) {        if (elem[child] > elem[parent]) {            int tmp = elem[child];            elem[child] = elem[parent];            elem[parent] = tmp;            child = parent;            parent = (child - 1) / 2;        } else {            break;        }    }}public void offer (int val) {    if (isFull()) {        //扩容        elem = Arrays.copyOf(elem,2*elem.length);    }    elem[usedSize++] = val;    shiftUp(usedSize - 1);}public boolean isFull() {    return usedSize == elem.length;}

此代码为传入一个新的子树，然后进行向上调整 即offer一个新元素，在添加完毕后我们将其按照大堆排好。

?2.4 操作-建堆?

下面我们给出一个数组，这个数组逻辑上可以看做一颗完全二叉树，但是还不是一个堆，现在我们通过算法，把它构建成一个堆。根节点左右子树不是堆，我们怎么调整呢？这里我们从倒数的第一个非叶子节点的子树开始调整，一直调整到根节点的树，就可以调整成堆。

图示（以大堆为例）：

// 建堆前int[] array = { 1,5,3,8,7,6 };// 建堆后int[] array = { 8,7,6,5,1,3 };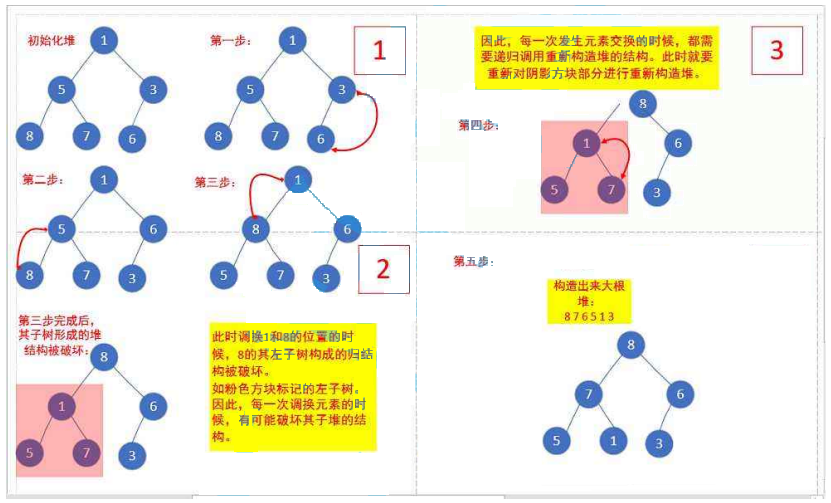

时间复杂度分析：

粗略估算，可以认为是在循环中执行向下调整，为 O(n * log(n))

（了解）实际上是 O(n)

堆排序中建堆过程时间复杂度O(n)怎么来的？

代码：

public static void createHeap(int[] array, int size) {    for (int i = (size - 1 - 1) / 2; i >= 0; i--) {        shiftDown(array, size, i);    }}

?3. 堆的应用-优先级队列?

?3.1 概念?

在很多应用中，我们通常需要按照优先级情况对待处理对象进行处理，比如首先处理优先级最高的对象，然后处理次高的对象。最简单的一个例子就是，在手机上玩游戏的时候，如果有来电，那么系统应该优先处理打进来的电话。

在这种情况下，我们的数据结构应该提供两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)

?3.2 内部原理?

优先级队列的实现方式有很多，但最常见的是使用堆来构建。

?3.3 操作-入队列?

过程（以大堆为例）：

首先按尾插方式放入数组比较其和其双亲的值的大小，如果双亲的值大，则满足堆的性质，插入结束否则，交换其和双亲位置的值，重新进行 2、3 步骤直到根结点

图示：

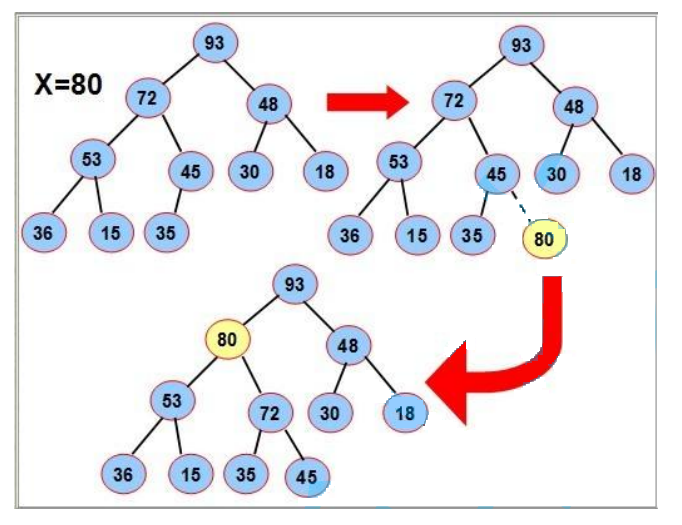
代码：

public static void shiftUp(int[] array, int index) {    while (index > 0) {        int parent = (index - 1) / 2;        if (array[parent] >= array[index]) {            break;        }        int t = array[parent];        array[parent] = array[index];        array[index] = t;        index = parent;    }}

?3.4 操作-出队列（优先级最高）?

为了防止破坏堆的结构，删除时并不是直接将堆顶元素删除，而是用数组的最后一个元素替换堆顶元素，然后通过向下调整方式重新调整成堆

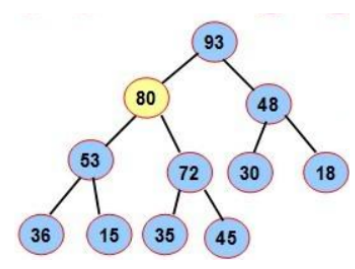
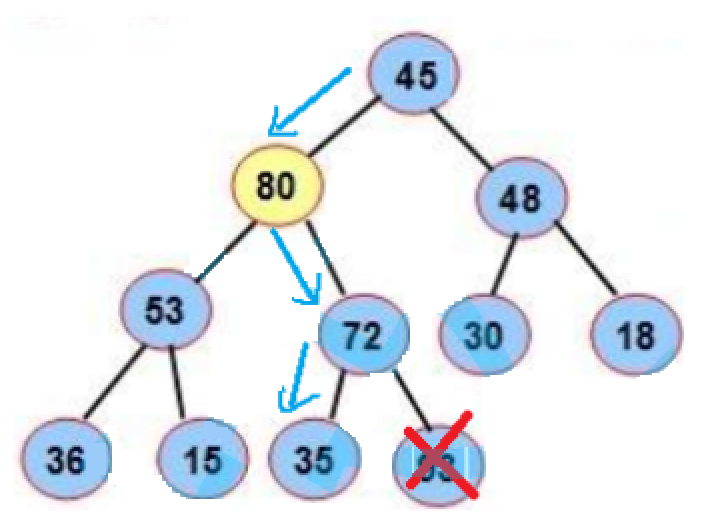
第一步：交换0下标和最后一个元素

第二步：调整0下标这棵树就可以了

?3.5 返回队首元素（优先级最高）?

返回堆顶元素即可

?3.6 代码?

public class MyPriorityQueue {    // 演示作用，不再考虑扩容部分的代码    private int[] elem = new int[100];    private int usedSize;public void offer (int val) {    if (isFull()) {        //扩容        elem = Arrays.copyOf(elem,2*elem.length);    }    elem[usedSize++] = val;    shiftUp(usedSize - 1);}public boolean isFull() {    return usedSize == elem.length;}public int poll() {    if (isEmpty()) {        throw new RuntimeException("优先级队列为空！");    }    int tmp = elem[0];    elem[0] = elem[usedSize - 1];    elem[usedSize - 1] = tmp;    usedSize--;    shiftDown(0,usedSize);    return tmp;}public int peek() {    if (isEmpty()) {        throw new RuntimeException("优先级队列为空！");    }    return elem[0];}public boolean isEmpty() {    return usedSize == 0;}}

?3.7 java 中的优先级队列?

PriorityQueue implements Queue

?4. 堆的其他应用-TopK 问题?

拜托，面试别再问我TopK了！！！

关键记得，找前 K 个最大的，要建 K 个大小的小堆

topK问题：给你100万个数据，让你找到前10个最大的元素。

思路一：对整体进行排序，输出前10个最大的元素。

思路二：用堆，即弹出10个最大的元素即可

思路三：

1、先把前3个元素，创建为小根堆

2、当前的堆为什么是小根堆，因为堆顶的元素，一定是当前K个元素当中最小的一个元素。如果有元素X比堆顶元素大，那么X这个元素，可能就是topK中的一个。

相反，如果是大根堆，那就不一定了

3、如果堆顶元素小，那么出堆顶元素，然后入当前比堆顶元素大的元素，再次调整为小根堆

时间复杂度：n*logn

总结：

1、如果要求前K个最大的元素，要建一个小根堆。(方便弹出堆顶的最小元素，然后重新排序为小根堆)

2、如果要求前K个最小的元素，要建一个大根堆。(方便弹出堆顶的最大元素，然后重新排序为大根堆)

3、第K大的元素。建一个小根堆，堆顶元素就是第K大的元素，堆内的元素就是前K个最大的元素。(X比堆顶元素大就放进去，然后重新排序为小根堆)

4、第K小的元素。建一个大根堆，堆顶元素就是第K小的元素，堆内的元素就是前K个最小的元素。(X比堆顶元素小就放进去，然后重新排序为大根堆)

例题：求前K个最小的元素：

import java.util.Arrays;import java.util.Comparator;import java.util.PriorityQueue;/** * Created with IntelliJ IDEA. * Description: * User: 晓星航 * Date: 2023-04-12 * Time: 19:07 */public class TopK {    /**     * 求数组当中的前K个最小的元素     * @param array     * @param k     * @return     */    public static int[] topK(int[]array, int k) {        //1、创建一个大小为K的大根堆        PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k, new Comparator<Integer>() {            @Override            public int compare(Integer o1, Integer o2) {                return o2-o1;            }        });        //2、遍历数组当中的元素，前k个元素放到队列当中        for (int i = 0; i < array.length; i++) {            if (maxHeap.size() < k) {                maxHeap.offer(array[i]);            } else {                //3、从第k+1个元素开始，每个元素和堆顶元素进行比较                int top = maxHeap.peek();                if (top > array[i]) {                    //3.1先弹出                    maxHeap.poll();                    //3.2后存入 注：offer时我们的堆重新自动排序为大根堆                    maxHeap.offer(array[i]);                }            }        }        //创建数组tmp来依次接受我们的maxHeap大根堆排序好的值        int[] tmp = new int[k];        for (int i = 0; i < k; i++) {            tmp[i] = maxHeap.poll();        }        return tmp;    }    public static void main(String[] args) {        int[] array = {18,21,8,10,34,12};        int[] tmp = topK(array,4);        System.out.println(Arrays.toString(tmp));    }}

? 5. 面试题?

查找和最小的K对数字

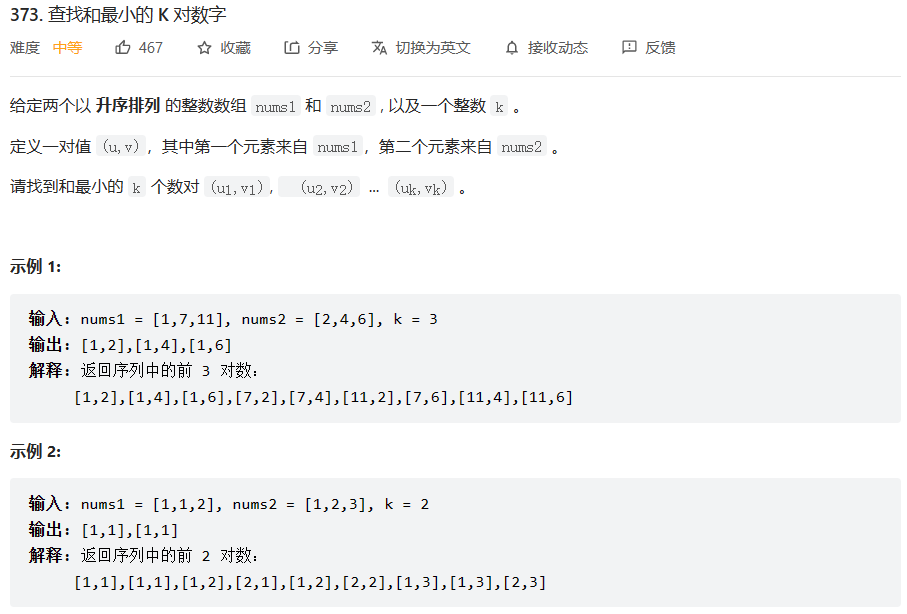
import java.util.*;class Solution {    public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {                PriorityQueue<List<Integer>> maxHeap = new PriorityQueue<>(k, new           Comparator<List<Integer>>() {            @Override            public int compare(List<Integer> o1, List<Integer> o2) {                return (o2.get(0)+o2.get(1)) - (o1.get(0)+o1.get(1));            }        });        for (int i = 0; i < Math.min(nums1.length,k); i++) {            for (int j = 0; j < Math.min(nums2.length,k); j++) {                if (maxHeap.size() < k) {                    List<Integer> tmpList = new ArrayList<>();                    tmpList.add(nums1[i]);                    tmpList.add(nums2[j]);                    maxHeap.offer(tmpList);                } else {                    int top = maxHeap.peek().get(0) + maxHeap.peek().get(1);                    if (top > nums1[i] + nums2[j]) {                        maxHeap.poll();                        List<Integer> tmpList = new ArrayList<>();                        tmpList.add(nums1[i]);                        tmpList.add(nums2[j]);                        maxHeap.offer(tmpList);                    }                }            }        }        List<List<Integer>> ret = new ArrayList<>();        for (int i = 0; i < k && !maxHeap.isEmpty(); i++) {            ret.add(maxHeap.poll());        }        return ret;    }}

?6. 堆的其他应用-堆排序?

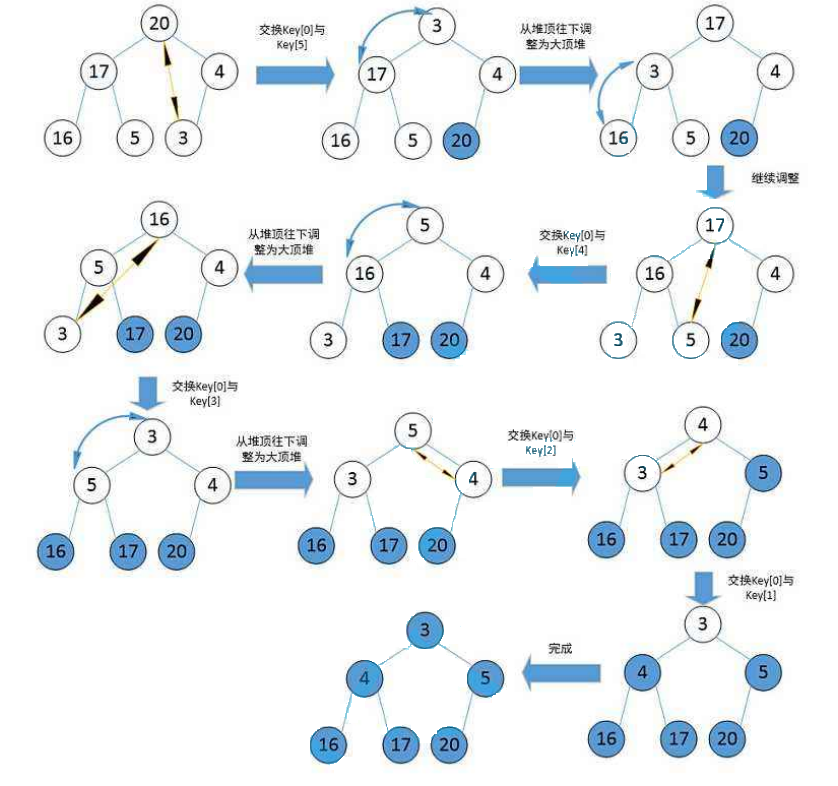
问：如果要将堆从小到大进行排列，我们应该选择大根堆还是小根堆来进行排序？

答：使用大根堆来进行排序、

思路如下：

1、调整为大根堆

2、0小标和最后1个未排序的元素进行交换即可

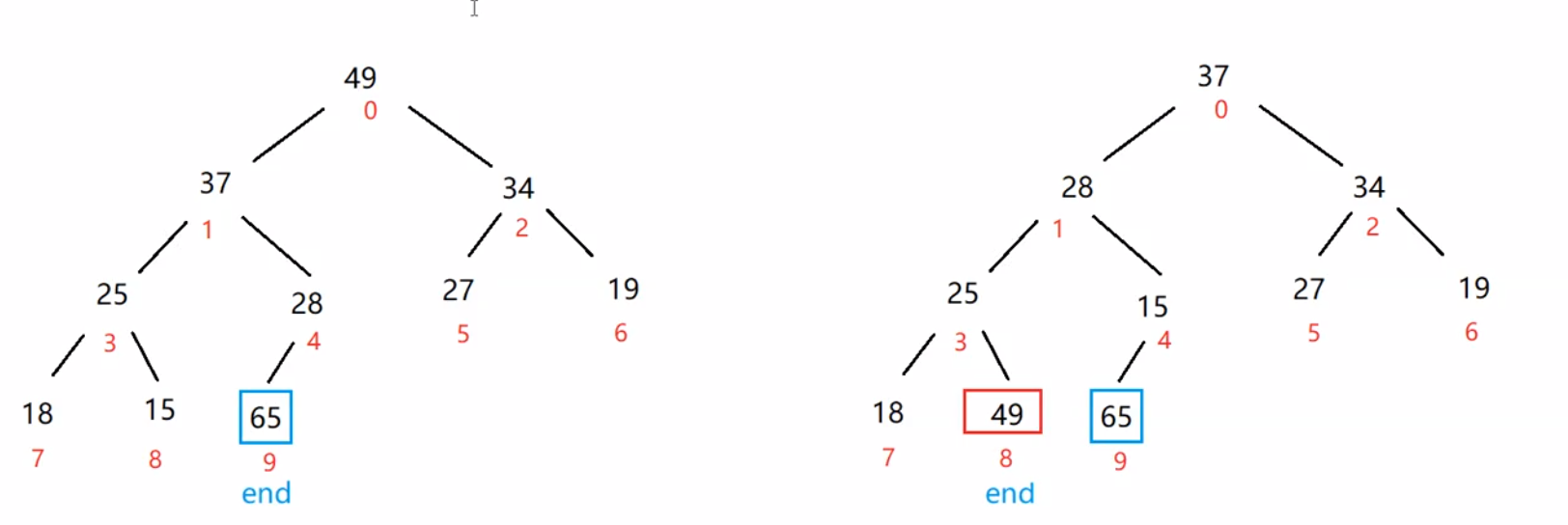
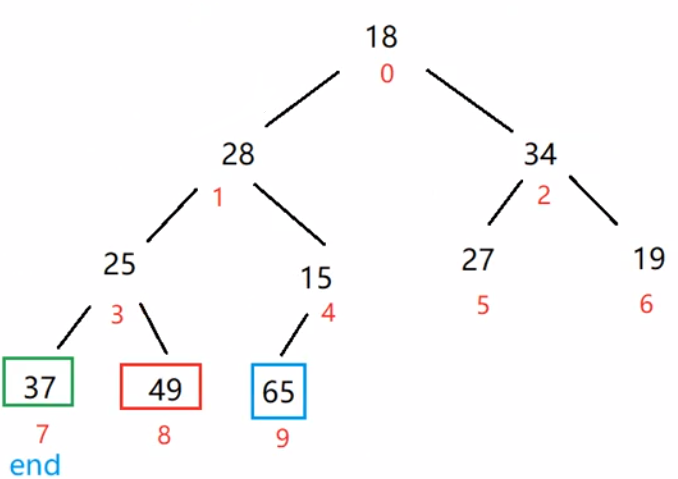
由上图可知当所有元素弹出后，我们的数组便自动排成了从小到大的顺序。

3、end–

感谢各位读者的阅读，本文章有任何错误都可以在评论区发表你们的意见，我会对文章进行改正的。如果本文章对你有帮助请动一动你们敏捷的小手点一点赞，你的每一次鼓励都是作者创作的动力哦！?