题目1:
已知系统函数:
H ( s ) = s − 1 s 2 + 2 s + 2 H(s)=\frac{s-1}{s^{2}+2s+2} H(s)=s2+2s+2s−1
求出该系统的零极点,并画出其零极点分布图。
roots:
roots(a)通常表示求解多项式方程a的根,其中a是一个多项式。在这里表示系统方程分子多项式的系数,也就是这里在求系统的极点。多项式方程的根是使得多项式等于零的变量值,也可以理解为多项式的零点或解。
markersize:
'markersize’参数用于指定标记的大小,这里设置为12。
legend()
用于在图形中添加图例,以便更好地说明数据的含义。
pzmap(b,a);
用于绘制零极点图(Pole-Zero Plot),展示有理传递函数的极点和零点在复平面上的分布情况。具体来说,它使用了MATLAB的pzmap函数,将有理传递函数的分子系数向量b和分母系数向量a作为参数传递给该函数。
代码中用了两种方法进行绘制,用于对比。
完整代码:
b=[1,-1];a=[1,2,2];ps=roots(a);zs=roots(b);subplot(121);plot(real(zs),imag(zs),'o',real(ps),imag(ps),'x','markersize',12);axis([-2,2,-2,2]);grid;%绘制网格线legend('零点','极点');subplot(122);pzmap(b,a);axis([-2,2,-2,2]);运行结果: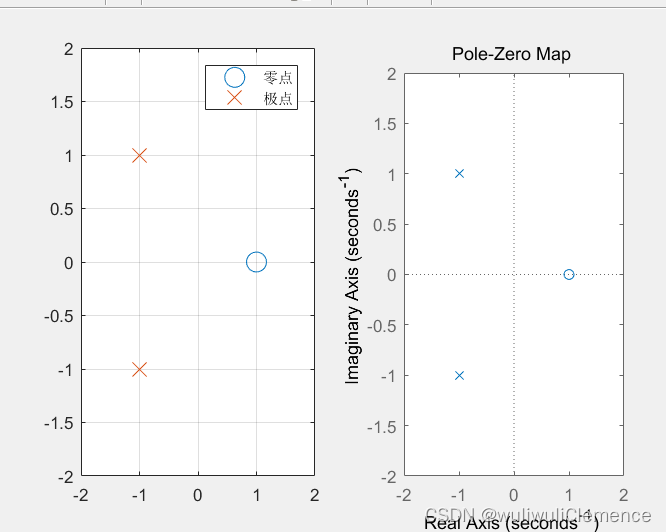
题目2:
已知系统函数分别为:
H 1 ( s ) = 1 s + 1 H1(s)=\frac{1}{s+1} H1(s)=s+11
H 2 ( s ) = 1 s 2 + 2 s + 17 H2(s)=\frac{1}{s^{2}+2s+17} H2(s)=s2+2s+171
求这些系统的零极点分布图及系统的冲激响应,并判断系统的稳定性。
仿照上面的题目,这次我们主要使用pzmap函数来进行求解零极点,同时用impluse函数进行求冲激响应。
a1=[1,1];b1=[1];subplot(221);impulse(b1,a1);axis([0,6,0,1]);subplot(222);pzmap(b1,a1);axis([-2,2,-1,1]);a2=[1,2,17];b2=[1];subplot(223);impulse(b2,a2);axis([0,5,-0.3,0.3]);subplot(224);pzmap(b2,a2);axis([-5,5,-5,5]);运行结果: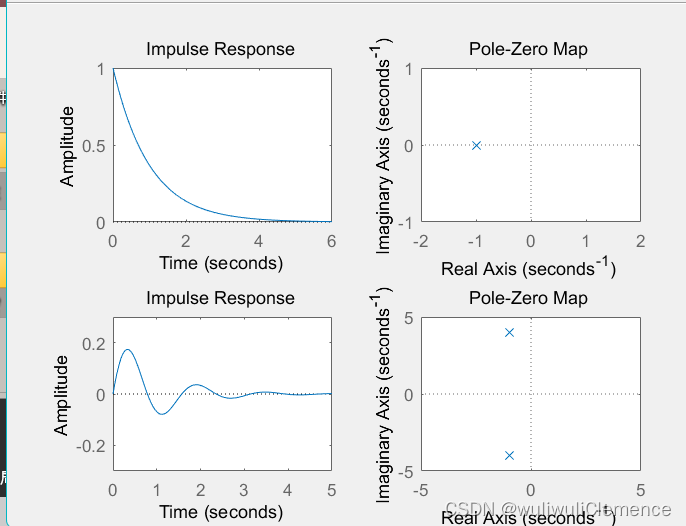
说明:axis用于确定横纵坐标的范围,可以根据计算结果选择合适的横纵坐标的范围进行绘制。此外,impulse和pzmap自带绘图功能,不用用plot画了。