ReflectionPad

一、反射填充1、一维反射填充1）调用方式2）实例（1）padding为整数（2）padding为2元组 2、二维反射填充1）调用方式2）实例（1）padding为整数（1）padding为4元组

一、反射填充

这种填充方式是以输入向量的边界为对称轴，以设定的padding大小为步长，将输入向量的边界内padding大小的元素，对称填充。设定padding时主要注意，padding必须小于向量所在维度的大小。

1、一维反射填充

1）调用方式

输入形状为(N,C,W_IN)或(C,W_IN)；输出形状为(N,C,W_out)或(C,W_out)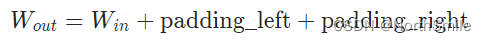；padding表示填充尺寸，可为整数或者2元组；padding为整数时，输入向量左右填充相同的大小；而padding为元组时可自定义向量左右分别填充多少；

torch.nn.ReflectionPad1d(padding)

2）实例

对于一维填充来说，其输入为N个宽度为W的向量，而每个元素对应有C个通道。此方式填充只针对他的宽度进行，填充点分别为向量左边和右边两个边界。不同的padding类型（整数或元组），决定了左右两边如何填充的方式。

（1）padding为整数

inp=torch.tensor([[[2., 3., 9., 1., 5.],         [6., 4., 0., 5., 0.]]])print(inp.shape)print("inp:",inp)pad=1out=nn.ReflectionPad1d(padding=pad)(inp)print("padding={},out:".format(pad),out)print(out.shape)

结果分析（绿线代表以此为轴，红色代表填充的元素）：
1）当padding=1时，表示向量左右两边均以边界为对称轴，填充宽度为1的元素。

torch.Size([1, 2, 5])inp: tensor([[[2., 3., 9., 1., 5.],         [6., 4., 0., 5., 0.]]])padding=1,out: tensor([[[3., 2., 3., 9., 1., 5., 1.],         [4., 6., 4., 0., 5., 0., 5.]]])torch.Size([1, 2, 7])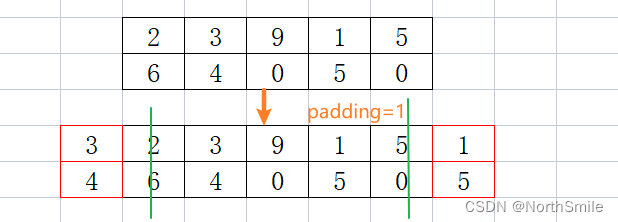

2）当padding=2时，表示向量左右两边均以边界为对称轴，填充宽度为2的元素。

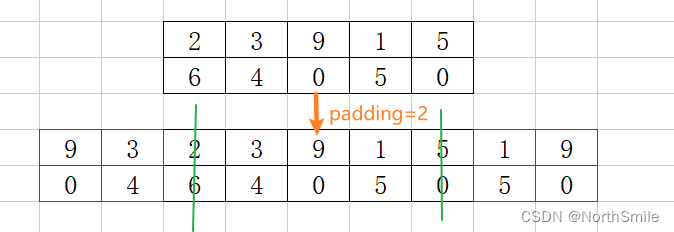
torch.Size([1, 2, 5])inp: tensor([[[2., 3., 9., 1., 5.],         [6., 4., 0., 5., 0.]]])padding=2,out: tensor([[[9., 3., 2., 3., 9., 1., 5., 1., 9.],         [0., 4., 6., 4., 0., 5., 0., 5., 0.]]])torch.Size([1, 2, 9])

（2）padding为2元组

inp=torch.tensor([[[2., 3., 9., 1., 5.],         [6., 4., 0., 5., 0.]]])print(inp.shape)print("inp:",inp)pad=(1,2)out=nn.ReflectionPad1d(padding=pad)(inp)print("padding={},out:".format(pad),out)print(out.shape)

结果分析：
1）当padding=(1,2)时，表示向量以边界为对称轴，左右两边分别填充宽度为1、2的元素。

torch.Size([1, 2, 5])inp: tensor([[[2., 3., 9., 1., 5.],         [6., 4., 0., 5., 0.]]])padding=(1, 2),out: tensor([[[3., 2., 3., 9., 1., 5., 1., 9.],         [4., 6., 4., 0., 5., 0., 5., 0.]]])torch.Size([1, 2, 8])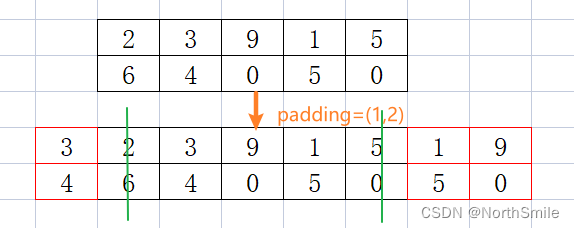

2、二维反射填充

1）调用方式

输入形状为(N,C,H_in,W_IN)或(C,H_in,W_IN)；输出形状为(N,C,H_out,W_out)或(C,H_out,W_out)；padding表示填充尺寸，可为整数或者4元组；padding为整数时，输入向量左右上下填充相同的大小；而padding为元组时可自定义向量左右上下分别填充多少；

torch.nn.ReflectionPad2d(padding)

2）实例

对于二维填充来说，其输入为N个宽度为H*W的数组，而每个元素对应有C个通道。此方式填充针对他的高度和宽度进行，填充点分别为上、下、左、右四个边界。不同的padding类型（整数或元组），决定了四个边界如何填充的方式。

（1）padding为整数

inp=torch.tensor([[[[8., 3., 6., 2., 7.],          [0., 8., 4., 9., 3.]],         [[3., 9., 6., 2., 7.],          [7., 8., 4., 6., 2.]],         [[1., 9., 0., 1., 4.],          [7., 8., 1., 0., 3.]]]])print(inp.shape)print("inp:",inp)pad=1out=nn.ReflectionPad2d(padding=pad)(inp)print("padding={},out:".format(pad),out)print(out.shape)

结果分析（图中白线、黑线代表以此为轴，红色、绿色块代表填充元素）：
1）当padding=1时，表示向量以边界为对称轴，左、右、上、下四个边界均填充宽度为1的元素。
填充按照左、右、上、下的顺序依次填充。

padding=1,out: tensor([[[[8., 0., 8., 4., 9., 3., 9.],          [3., 8., 3., 6., 2., 7., 2.],          [8., 0., 8., 4., 9., 3., 9.],          [3., 8., 3., 6., 2., 7., 2.]],         [[8., 7., 8., 4., 6., 2., 6.],          [9., 3., 9., 6., 2., 7., 2.],          [8., 7., 8., 4., 6., 2., 6.],          [9., 3., 9., 6., 2., 7., 2.]],         [[8., 7., 8., 1., 0., 3., 0.],          [9., 1., 9., 0., 1., 4., 1.],          [8., 7., 8., 1., 0., 3., 0.],          [9., 1., 9., 0., 1., 4., 1.]]]])torch.Size([1, 3, 4, 7])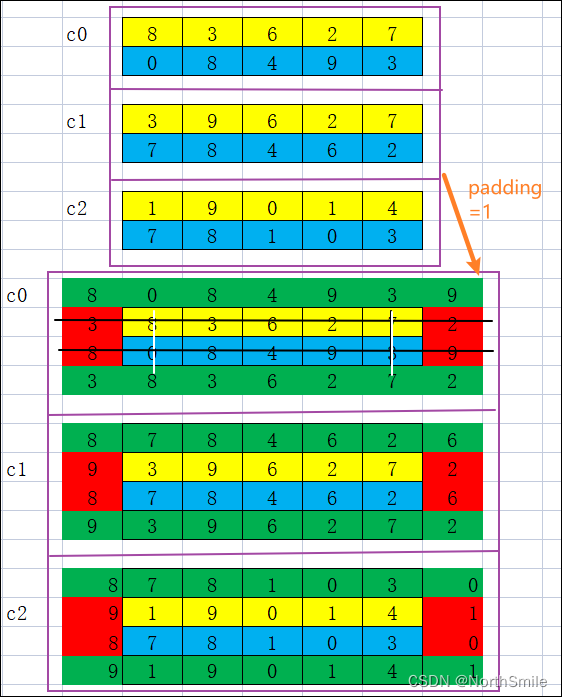

（1）padding为4元组

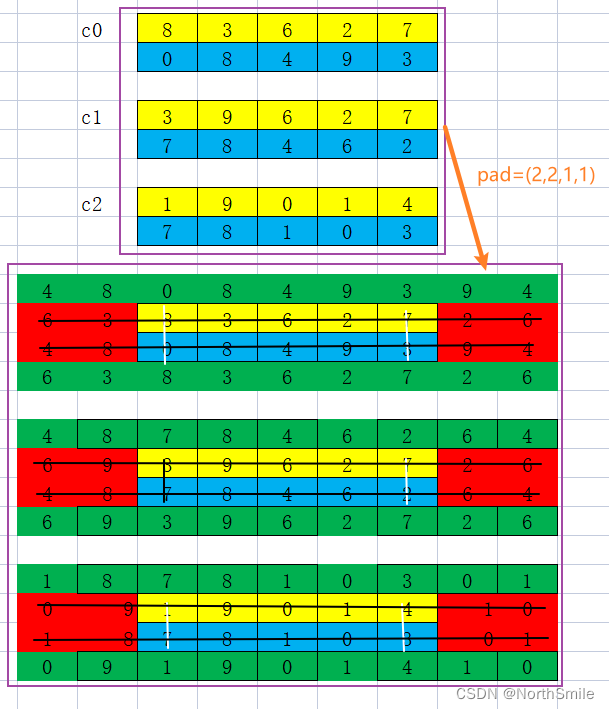
inp=torch.tensor([[[[8., 3., 6., 2., 7.],          [0., 8., 4., 9., 3.]],         [[3., 9., 6., 2., 7.],          [7., 8., 4., 6., 2.]],         [[1., 9., 0., 1., 4.],          [7., 8., 1., 0., 3.]]]])pad=(2,2,1,1)out=nn.ReflectionPad2d(padding=pad)(inp)print("padding={},out:".format(pad),out)print(out.shape)

结果分析：
1）当padding=(2,2,1,1)时，表示向量以左、右、上、下边界为对称轴，左、右、上、下分别填充宽度为2,2,1,1的元素。

padding=(2, 2, 1, 1),out: tensor([[[[4., 8., 0., 8., 4., 9., 3., 9., 4.],          [6., 3., 8., 3., 6., 2., 7., 2., 6.],          [4., 8., 0., 8., 4., 9., 3., 9., 4.],          [6., 3., 8., 3., 6., 2., 7., 2., 6.]],         [[4., 8., 7., 8., 4., 6., 2., 6., 4.],          [6., 9., 3., 9., 6., 2., 7., 2., 6.],          [4., 8., 7., 8., 4., 6., 2., 6., 4.],          [6., 9., 3., 9., 6., 2., 7., 2., 6.]],         [[1., 8., 7., 8., 1., 0., 3., 0., 1.],          [0., 9., 1., 9., 0., 1., 4., 1., 0.],          [1., 8., 7., 8., 1., 0., 3., 0., 1.],          [0., 9., 1., 9., 0., 1., 4., 1., 0.]]]])torch.Size([1, 3, 4, 9])