线性回归实现Abalone鲍鱼年龄预测
文章目录
线性回归实现Abalone鲍鱼年龄预测一、环境准备数据集简介 二、线性回归基础知识什么是线性回归?“最小二乘法” 求解线性回归问题 三、Python代码四、结果分析前面我们使用手动编写,后面通过sklearn第三方库来与我们手写的模型进行对比
一、环境准备
原始数据集下载及说明:https://archive.ics.uci.edu/ml/datasets/abalone
Python 3.9.13+PyCharm 2022.2.3 (Professional Edition) 或者 jupyter什么的自己选择
sklearn==1.1.3 pip install -U scikit-learn
数据集简介
官方的文档介绍如下:
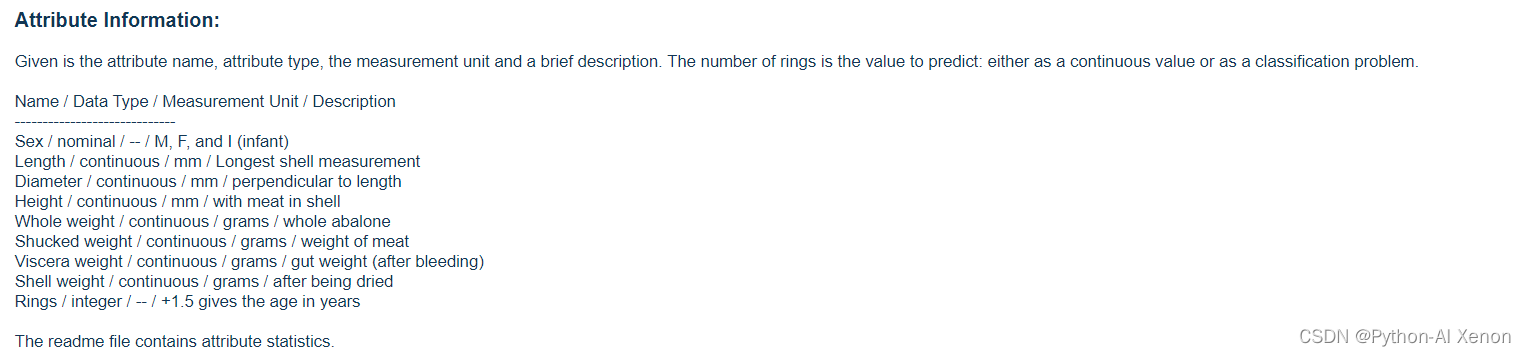
从中我们可以看到原始数据集共有4177条数据,其中每条数据包含9个特征,见下表
| 名称 | 数据类型 | 测量单位 | 描述 |
|---|---|---|---|
| 性别 | 标称 | – | M、F和I(婴儿) |
| 长度 | 连续 | mm | 最长外壳测量 |
| 直径 | 连续 | mm | 垂直于长度 |
| 高度 | 连续 | mm | 壳中有肉 |
| 全重 | 连续 | g | 整只鲍鱼 |
| 屠宰重量 | 连续 | g | 肉的重量 |
| 内脏重量 | 连续 | g | 肠道重量(出血后) |
| 壳重 | 连续 | g | 干燥后 |
| Rings | integer | – | +1.5表示年龄(年) |
同样的,我们还是可以不用太关心这些特征是什么并不影响我们后面对鲍鱼年龄的预测.
二、线性回归基础知识
什么是线性回归?
在统计学中,线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。


“最小二乘法” 求解线性回归问题


推荐参考: 用人话讲明白线性回归LinearRegression
三、Python代码
# -*- coding: utf-8 -*-# @Author : yxn# @Date : 2022/11/12 18:49 # @IDE : PyCharm(2022.2.3) Python3.9.13import numpy as npfrom scipy.stats import pearsonrfrom sklearn import linear_modelclass LinearRegression: """手动实现线性回归模型的LinearRegression类""" def __init__(self): self.w = None # 增广权重向量 self.n_features = None # 用于存储样本属性的数量 def fit(self, X, y): """ 在进行异常判断之后,将样本转化为增广特征向量,然后使用公式w=(X^TX)^{-1}X^Ty, 利用numpy的dot与linalg.inv函数,实现最小二乘法。(需要判断样本数量是否大于属性数量) :param X: 训练属性集X训 :param y: 练标签集y :return: 最优参数w """ assert isinstance(X, np.ndarray) and isinstance(y, np.ndarray) # assert(断言)用于判断输入值是否异常 assert X.ndim == 2 and y.ndim == 1 assert y.shape[0] == X.shape[0] n_samples = X.shape[0] self.n_features = X.shape[1] extra = np.ones((n_samples,)) X = np.c_[X, extra] if self.n_features < n_samples: self.w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y) # 使用最小二乘法求权重w,np.linalg.inv:求逆矩阵 else: raise ValueError('dont have enough samples') def predict(self, X): """ 用于执行测试,输入测试样本集,转化成增广特征向量,返回预测标签。 :param X: 测试属性集X :return: 预测标签y_ """ n_samples = X.shape[0] extra = np.ones((n_samples,)) X = np.c_[X, extra] if self.w is None: raise RuntimeError('cant predict before fit') y_ = X.dot(self.w) return y_def loadDataSet(fileName): """ 数据集每一行为一个样本,其中最后一个值为标签,其余值为属性。 根据文件名,依次读取每一行,将属性与标签转化为float类型,存储在列表中,再存入属性集xArr,标签集yArr :param fileName: 数据集文件名fileName :return: 属性集xArr,标签集yArr(转化成numpy的array类型) """ numFeat = len(open(fileName).readline().split('\t')) - 1 xArr = [] yArr = [] fr = open(fileName) for line in fr.readlines(): lineArr = [] curLine = line.strip().split('\t') for i in range(numFeat): lineArr.append(float(curLine[i])) xArr.append(lineArr) yArr.append(float(curLine[-1])) return np.array(xArr), np.array(yArr)def main(): """(顶层代码)线性回归模型完成鲍鱼年龄的预测 :return: """ # 使用loadDataSet函数读取文件abalone.txt,将返回的属性集、标签集赋值给X, y X, y = loadDataSet(r"E:\wynuJunior\模式识别\5回归实践\abalone.csv") # #===================手写LinearRegression==============================# # lr = LinearRegression() # 实例化LinearRegression()模型 lr.fit(X, y) # 使用fit方法进行训练 y_pre = lr.predict(X) # 使用predict方法,对训练时的属性集再进行预测 print("手写线性回归预测标签:", y_pre) # #===================sklearn模块中LinearRegression=======================# # sklearn_lr = linear_model.LinearRegression() # 调用sklearn模块中的线性回归模型 sklearn_lr.fit(X, y) # 使用fit方法进行训练 sklearn_y_pre = sklearn_lr.predict(X) # 使用predict方法,对训练时的属性集再进行预测 print("sklearn模块线性回归预测标签:\n", sklearn_y_pre) # 使用pearsonr相关系数,比较两种预测结果的差距。(顶层代码) # pearsonr函数可以从scipy.stats模块导入,输入两个序列,比较其相似性, # 现将手写模型的结果y_pre与sk-learn模型的结果sklearn_y_pre # 返回两个数值,分别代表相似性与置信度,其中第一个数值(相似性)应当为1,否则代表手写代码出现错误。 print('手动编写的线性回归与sklearn中的线性回归预测结果相似性为: ', pearsonr(y_pre, sklearn_y_pre)[0])if __name__ == '__main__': main() # 程序执行入口补充内容: 岭回归 # -*- coding: utf-8 -*-# @Author : yxn# @Date : 2022/11/23 22:36 # @IDE : PyCharm(2022.2.3) Python3.9.13import numpy as npfrom sklearn import linear_modeldef loadDataSet(fileName): """ 数据集每一行为一个样本,其中最后一个值为标签,其余值为属性。 根据文件名,依次读取每一行,将属性与标签转化为float类型,存储在列表中,再存入属性集xArr,标签集yArr :param fileName: 数据集文件名fileName :return: 属性集xArr,标签集yArr(转化成numpy的array类型) """ numFeat = len(open(fileName).readline().split('\t')) - 1 xArr = [] yArr = [] fr = open(fileName) for line in fr.readlines(): lineArr = [] curLine = line.strip().split('\t') for i in range(numFeat): lineArr.append(float(curLine[i])) xArr.append(lineArr) yArr.append(float(curLine[-1])) return np.array(xArr), np.array(yArr)def Ridge_regression(): """岭回归模型完成鲍鱼年龄的预测 # 官方文档 https://scikit-learn.org/dev/modules/generated/sklearn.linear_model.Ridge.html """ # 使用loadDataSet函数读取文件abalone.txt,将返回的属性集、标签集赋值给X, y X, y = loadDataSet(r"E:\wynuJunior\模式识别\5回归实践\abalone.csv") # #===================sklearn模块中岭回归=======================# # # l2正则化线性最小二乘。alpha是L2正则化常数,它乘以L2项,控制正则化的力量。 # 当' alpha = 0 '时,目标等价于普通最小值平方. ridge_reg = linear_model.Ridge(alpha=0., solver='lsqr') # 岭回归 ridge_reg.fit(X, y) # 使用fit方法进行训练 ridge_y_pre = ridge_reg.predict(X) # 使用predict方法,对训练时的属性集再进行预测 print("sklearn模块岭回归预测标签:\n", ridge_y_pre)if __name__ == '__main__': Ridge_regression() # 程序执行入口四、结果分析
运行结果如下:
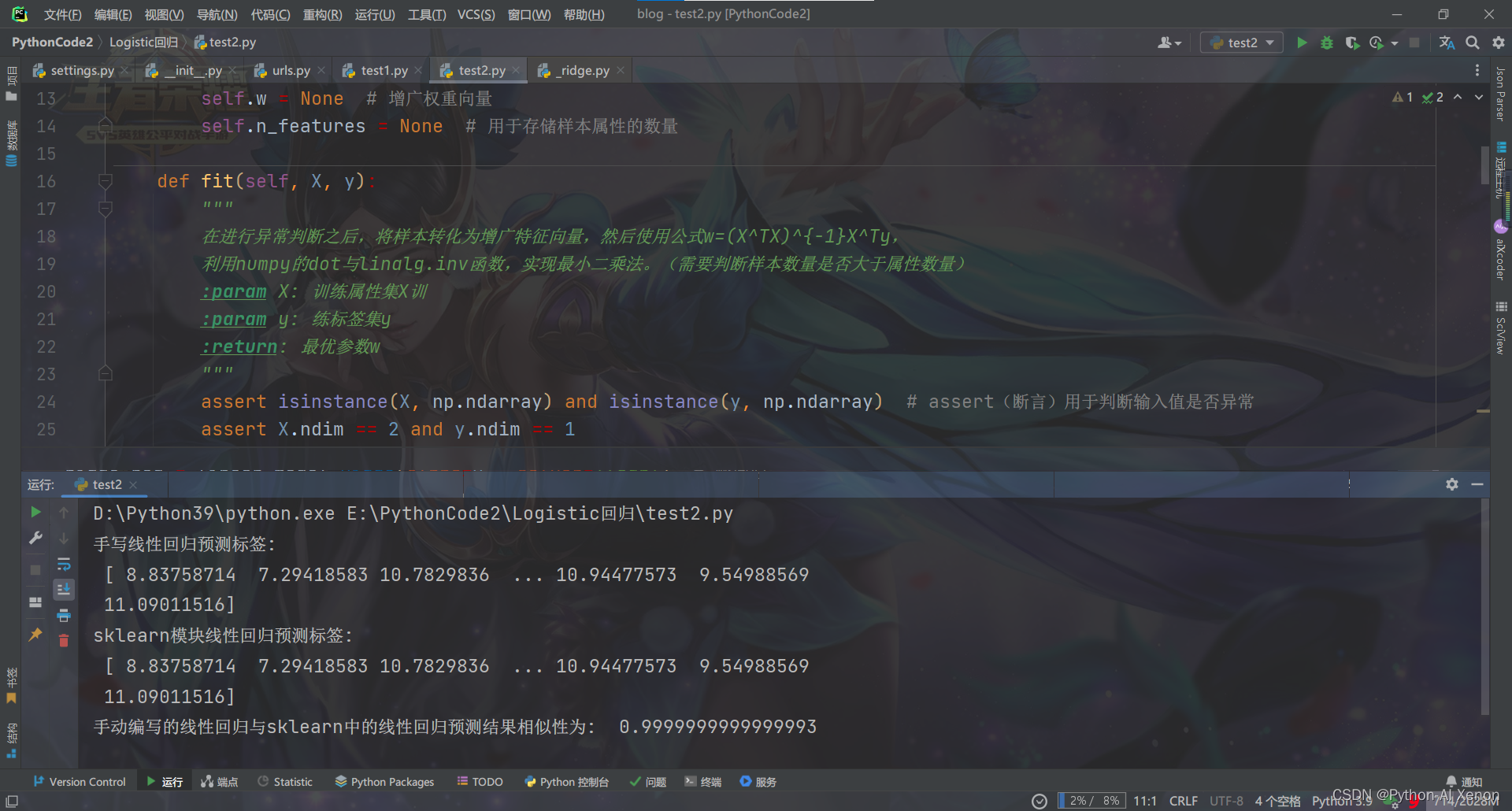
可以看到我们是输出标签都是一样的,而且预测结果相似性也达到了99.9%,可见手写的线性回归是正确的.