目录
A、阶乘求和
Ⅰ、题目解读
Ⅱ、代码
B、幸运数字
Ⅰ、题目解读
Ⅱ、代码
C: 数组分割(时间限制: 1.0s 内存限制: 512.0MB)
D、矩形总面积(时间限制: 1.0s 内存限制: 512.0MB)
Ⅰ、题目解读
Ⅱ、代码
E、蜗牛(时间限制: 1.0s 内存限制: 512.0MB)
F、合并区域 (时间限制: 2.0s 内存限制: 512.0MB)
Ⅰ、题目解读
Ⅱ、代码
G、买二赠一(时间限制: 1.0s 内存限制: 512.0MB)
Ⅰ、题目解读
H、合并石子(时间限制: 1.0s 内存限制: 512.0MB)
I、最大开支(时间限制: 1.0s 内存限制: 512.0MB )
Ⅰ、题目解读
J、魔法阵(时间限制: 1.0s 内存限制: 512.0MB )
总结
A、阶乘求和
【问题描述】 令 S = 1! + 2! + 3! + ... + 202320232023! ,求 S 的末尾 9 位数字。 提示:答案首位不为 0 。Ⅰ、题目解读
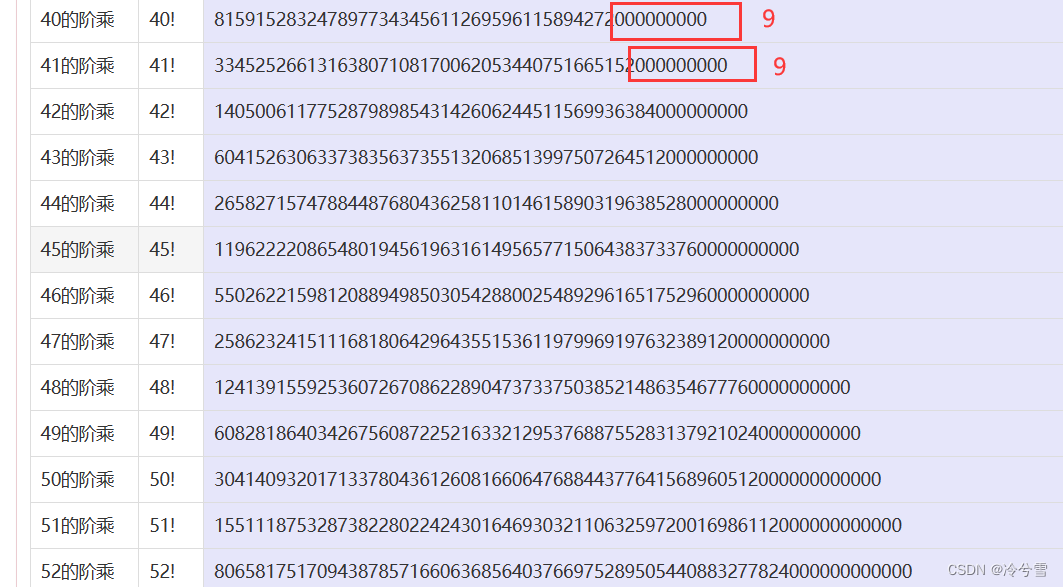
一看到三个2023的巨大数字,我想大家应该都人都麻了。但是我想说这是官方的骗术,因为题目说要求末尾的9位数,其实我想告诉大家当加到40多的阶乘时,这个阶乘和后面的9位数就不会发生改变了。
Ⅱ、代码
public class Main { public static void main(String[] args) { long start=1; String s="202320232023"; long end= Long.parseLong(s); long sum=0; long cj=1; while (start<=end){ cj*=start; cj%=1000000000; sum+=cj; sum%=1000000000; start++; if (start>40) System.out.println(sum); } System.out.println(sum); }}看运行
20940313420940313420940313420940313420940313420940313420940313...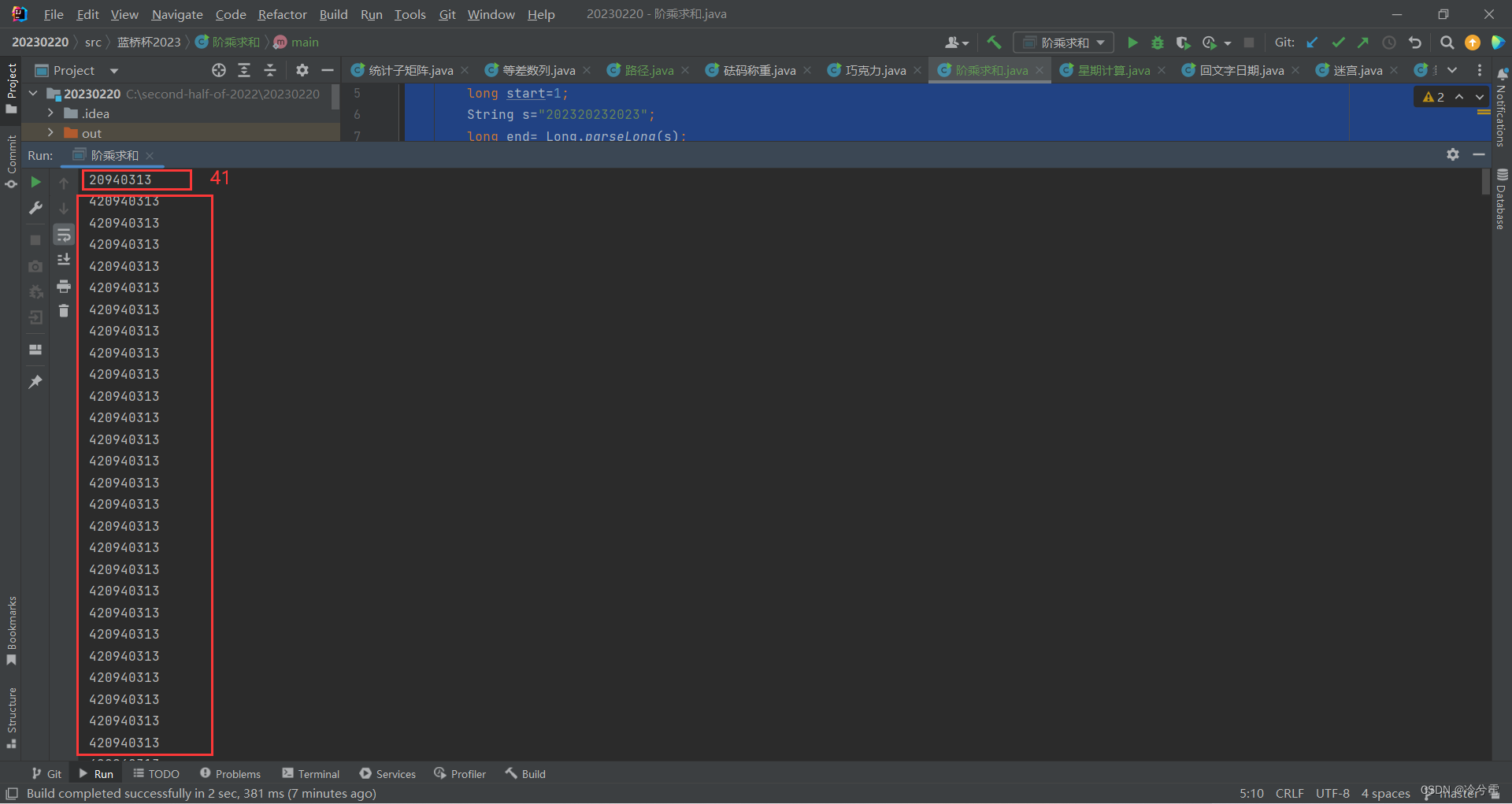
这是因为40的阶乘之后后面 9位数都是0,所以阶乘之和末尾9位数不会再发生改变!
B、幸运数字
【问题描述】 哈沙德数是指在某个固定的进位制当中,可以被各位数字之和整除的正整 数。例如 126 是十进制下的一个哈沙德数,因为 (126) 10 mod (1+2+6) = 0 ; 126 也是八进制下的哈沙德数,因为 (126) 10 = (176) 8 , (126) 10 mod (1 + 7 + 6) = 0 ; 同时 126 也是 16 进制下的哈沙德数,因为 (126) 10 = (7 e ) 16 , (126) 10 mod (7 + e ) = 0 。小蓝认为,如果一个整数在二进制、八进制、十进制、十六进制下均为 哈沙德数,那么这个数字就是幸运数字,第 1 至第 10 个幸运数字的十进制表示 为:1 , 2 , 4 , 6 , 8 , 40 , 48 , 72 , 120 , 126 . . . 。现在他想知道第 2023 个幸运数 字是多少?你只需要告诉小蓝这个整数的十进制表示即可。Ⅰ、题目解读
这题就是考察大家的进制转换,数据量也不大。直接看代码吧!
Ⅱ、代码
public class { public static void main(String[] args) { int j=0; for (int i=1;i<10000000;i++){ if (BaseConversion(i)){ j++; if (j==2023){ System.out.println(i);//215040 break; } } } } public static boolean BaseConversion(int n){ //十进制 int sum=0; int x=n; while (x!=0){ sum+=(x%10); x/=10; } if (n%sum!=0) return false; //二进制 sum=0; x=n; while (x!=0){ sum+=(x%2); x/=2; } if (n%sum!=0) return false; //八进制 sum=0; x=n; while (x!=0){ sum+=(x%8); x/=8; } if (n%sum!=0) return false; //十六进制 int[] arr={0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}; sum=0; x=n; while (x!=0){ sum+=(arr[x%16]); x/=16; } if (n%sum!=0) return false; return true; }}C: 数组分割(时间限制: 1.0s 内存限制: 512.0MB)
时间限制 : 1.0s 内存限制 : 512.0MB 本题总分: 10 分 【问题描述】 小蓝有一个长度为 N 的数组 A = [ A 0 , A 1 , . . . , A N − 1 ] 。现在小蓝想要从 A 对应的数组下标所构成的集合 I = { 0 , 1 , 2 , . . . , N − 1 } 中找出一个子集 R 1 ,那么 R 1在 I 中的补集为 R 2 。记 S 1 = ∑ r ∈ R 1 A r , S 2 = ∑ r ∈ R 2 A r,我们要求 S 1 和 S 2 均为 偶数,请问在这种情况下共有多少种不同的 R 1。当 R1 或 R 2 为空集时我们将 S 1 或 S 2 视为 0。【输入格式】 第一行一个整数 T ,表示有 T 组数据。 接下来输入 T 组数据,每组数据包含两行:第一行一个整数 N ,表示数组 A 的长度;第二行输入 N 个整数从左至右依次为 A 0 , A 1 , . . . , A N − 1 ,相邻元素之 间用空格分隔。 【输出格式】 对于每组数据,输出一行,包含一个整数表示答案,答案可能会很大,你 需要将答案对 1000000007 进行取模后输出。 【样例输入】
226 621 64D、矩形总面积(时间限制: 1.0s 内存限制: 512.0MB)
【问题描述】 平面上有个两个矩形 R 1 和 R 2 ,它们各边都与坐标轴平行。设 ( x 1 , y 1 ) 和 (x 2 , y 2 ) 依次是 R 1 的左下角和右上角坐标, ( x 3 , y 3 ) 和 ( x 4 , y 4 ) 依次是 R 2 的左下 角和右上角坐标,请你计算 R 1 和 R 2 的总面积是多少? 注意:如果 R 1 和 R 2 有重叠区域,重叠区域的面积只计算一次。 【输入格式】 输入只有一行,包含 8 个整数,依次是: x 1 , y 1 , x 2 , y 2 , x 3 , y 3 , x 4 和 y 4 。 【输出格式】 一个整数,代表答案。 【样例输入】2 1 7 4 5 3 8 622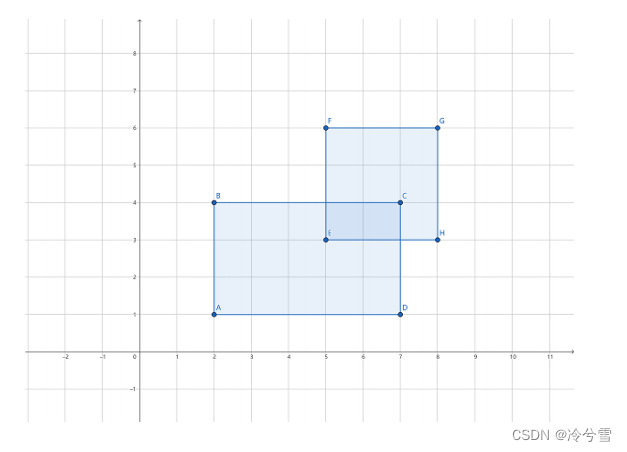
【评测用例规模与约定】 对于 20 % 的数据, R 1 和 R 2 没有重叠区域。 对于 20 % 的数据,其中一个矩形完全在另一个矩形内部。 对于 50 % 的数据,所有坐标的取值范围是 [0 , 10³ ] 。 对于 100 % 的数据,所有坐标的取值范围是 [0 , 10⁵ ]
Ⅰ、题目解读
这题有两种解法,自己数组去求,但是可能数据量过大会爆栈。第二种就是公式直接求解,这时求两个矩形相交的面积改怎么求?
矩形相交要使条件成立,即min(x2,x4)-max(x1,x3)>=0 且min(y2,y4)-max(y1,y3)>=0
如果条件成立,则相交矩形面积为:(min(x2,x4)-max(x1,x3))* (min(y2,y4)-max(y1,y3))
Ⅱ、代码
import java.util.Scanner;public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); int x1 = sc.nextInt(); int y1 = sc.nextInt(); int x2 = sc.nextInt(); int y2 = sc.nextInt(); int x3 = sc.nextInt(); int y3 = sc.nextInt(); int x4 = sc.nextInt(); int y4 = sc.nextInt(); long area1 = (long) (x2 - x1) * (y2 - y1); // 计算第一个矩形的面积 long area2 = (long) (x4 - x3) * (y4 - y3); // 计算第二个矩形的面积 long overlapArea=0; long l = Math.min(x2, x4) - Math.max(x1, x3); long w= Math.min(y2,y4)-Math.max(y1,y3); if (l >=0&&w >=0){ overlapArea= l * w; } long Area = area1 + area2 - overlapArea; // 总面积 System.out.println(Area); // 输出总面积 }}E、蜗牛(时间限制: 1.0s 内存限制: 512.0MB)
【问题描述】 这天,一只蜗牛来到了二维坐标系的原点。 在 x 轴上长有 n 根竹竿。它们平行于 y 轴,底部纵坐标为 0 ,横坐标分别 为 x 1 , x 2 , ..., x n 。竹竿的高度均为无限高,宽度可忽略。蜗牛想要从原点走到第 n 个竹竿的底部也就是坐标 ( x n , 0) 。它只能在 x 轴上或者竹竿上爬行,在 x 轴 上爬行速度为 1 单位每秒;由于受到引力影响,蜗牛在竹竿上向上和向下爬行 的速度分别为 0 . 7 单位每秒和 1 . 3 单位每秒。 为了快速到达目的地,它施展了魔法,在第 i 和 i + 1 根竹竿之间建立了传 送门(0 < i < n ),如果蜗牛位于第 i 根竹竿的高度为 a i 的位置 ( x i , a i ) ,就可以 瞬间到达第 i + 1 根竹竿的高度为 b i +1 的位置 ( x i +1 , b i +1 ), 请计算蜗牛最少需要多少秒才能到达目的地。 【输入格式】 输入共 1 + n 行,第一行为一个正整数 n ; 第二行为 n 个正整数 x 1 , x 2 , . . . , x n ; 后面 n − 1 行,每行两个正整数 a i , b i +1 。 【输出格式】 输出共一行,一个浮点数表示答案( 四舍五入保留两位小数 )。 【样例输入】31 10 111 12 1【样例输出】
4.20F、合并区域 (时间限制: 2.0s 内存限制: 512.0MB)
【问题描述】 小蓝在玩一款种地游戏。现在他被分配给了两块大小均为 N × N 的正方形 区域。这两块区域都按照 N × N 的规格进行了均等划分,划分成了若干块面积 相同的小区域,其中每块小区域要么是岩石,要么就是土壤,在垂直或者水平 方向上相邻的土壤可以组成一块土地。现在小蓝想要对这两块区域沿着边缘进 行合并,他想知道合并以后可以得到的最大的一块土地的面积是多少(土地的 面积就是土地中土壤小区域的块数)? 在进行合并时,小区域之间必须对齐。可以在两块方形区域的任何一条边 上进行合并,可以对两块方形区域进行 90 度、 180 度、 270 度、 360 度的旋转, 但不可以进行上下或左右翻转,并且两块方形区域不可以发生重叠。 【输入格式】 第一行一个整数 N 表示区域大小。 接下来 N 行表示第一块区域,每行 N 个值为 0 或 1 的整数,相邻的整数 之间用空格进行分隔。值为 0 表示这块小区域是岩石,值为 1 表示这块小区域 是土壤。 再接下来 N 行表示第二块区域,每行 N 个值为 0 或 1 的整数,相邻的整 数之间用空格进行分隔。值为 0 表示这块小区域是岩石,值为 1 表示这块小区 域是土壤。 【输出格式】 一个整数表示将两块区域合并之后可以产生的最大的土地面积。 【样例输入】40 1 1 01 0 1 11 0 1 01 1 1 00 0 1 00 1 1 01 0 0 01 1 1 115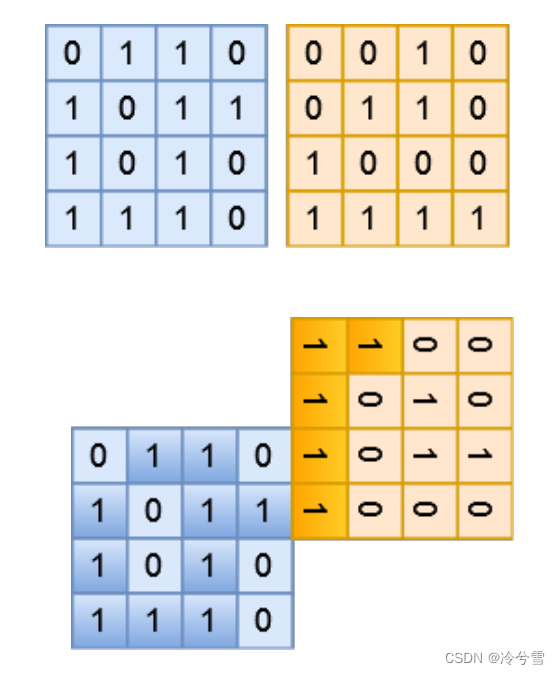
Ⅰ、题目解读
题目会给你两块土地,你可以进行两块土地的“缝合”,求最大的连续的土地。 最大土地有三种情况 ①、左右连接成一块最大的土地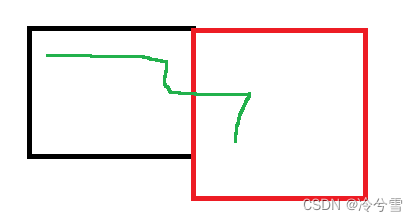
②、单独一边中间是最大的土地
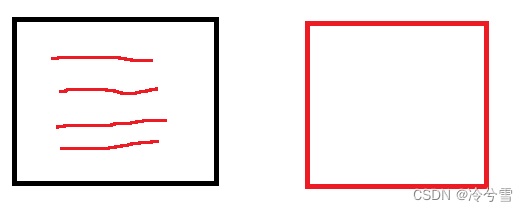
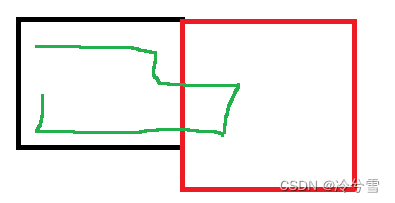
③、因为另一块土地的连接而导致原本不连接的土地也连接成新的土地(这种情况是我没想到的)
我只想到了前面两种情况,如果要算上第三种情况的话就应该直接使用暴力求解(毕竟数据量并不是很大),不断拼接,求最大连续的土地。我的代码也只是符合前面两种情况,有正确代码还请大佬给出。万分感谢。
Ⅱ、代码
import java.awt.*;import java.util.ArrayList;import java.util.HashSet;import java.util.List;import java.util.Scanner;public class Main { static class Point{ int x,y; public Point(int x, int y) { this.x = x; this.y = y; } } public static void main(String[] args) { Scanner sc=new Scanner(System.in); int n=sc.nextInt(); int[][] arr1=new int[n+2][n+2];//第一个矩阵 int[][] arr2=new int[n+2][n+2];//第二个矩阵 for (int i=1;i<=n;i++) for (int j=1;j<=n;j++){ arr1[i][j]=sc.nextInt(); } for (int i=1;i<=n;i++) for (int j=1;j<=n;j++){ arr2[i][j]=sc.nextInt(); } int max=0; for (int i=1;i<=n;i++) for (int j=1;j<=n;j++){ if (arr1[i][j]==1){ length(arr1,i,j); List<Point> list=new ArrayList<>(set); for (Point p:list) arr1[p.x][p.y]=sum; max=Math.max(max,sum);//防止矩阵里面是最大的 sum=0; set.clear(); } } for (int i=1;i<=n;i++) for (int j=1;j<=n;j++){ if (arr2[i][j]==1){ length(arr2,i,j); List<Point> list=new ArrayList<>(set); for (Point p:list) arr2[p.x][p.y]=sum; max=Math.max(max,sum);//防止矩阵里面是最大的 sum=0; set.clear(); } } int l=0; int r=0; //求四边的最大值然后拼接 //两行 for (int i=1;i<=n;i+=(n-1)) for (int j=1;j<=n;j++){ l=Math.max(l,arr1[i][j]); r=Math.max(r,arr2[i][j]); } //两列 for (int i=1;i<=n;i++) for (int j=1;j<=n;j+=(n-1)){ l=Math.max(l,arr1[i][j]); r=Math.max(r,arr2[i][j]); } max=Math.max(max,l+r); System.out.println(max); } static int sum=0; static HashSet<Point> set=new HashSet<>(); public static void length(int[][] arr, int i, int j){ sum++; arr[i][j]=0; Point p=new Point(i,j); set.add(p); if (arr[i-1][j]==1) length(arr,i-1,j); if (arr[i+1][j]==1) length(arr,i+1,j); if (arr[i][j-1]==1) length(arr,i,j-1); if (arr[i][j+1]==1) length(arr,i,j+1); }}G、买二赠一(时间限制: 1.0s 内存限制: 512.0MB)
【问题描述】 某商场有 N 件商品,其中第 i 件的价格是 A i 。现在该商场正在进行 “ 买二 赠一” 的优惠活动,具体规则是: 每购买 2 件商品,假设其中较便宜的价格是 P (如果两件商品价格一样, 则 P 等于其中一件商品的价格),就可以从剩余商品中任选一件价格不超过 P /2 的商品,免费获得这一件商品。可以通过反复购买 2 件商品来获得多件免费商 品,但是每件商品只能被购买或免费获得一次。 小明想知道如果要拿下所有商品(包含购买和免费获得),至少要花费多少钱? 【输入格式】 第一行包含一个整数 N 。 第二行包含 N 个整数,代表 A 1 , A 2 , A 3 , . . . , A N 【输出格式】 输出一个整数,代表答案。 【样例输入】71 4 2 8 5 7 1【样例输出】
25【样例说明】
小明可以先购买价格 4 和 8 的商品,免费获得一件价格为 1 的商品;再后 买价格为 5 和 7 的商品,免费获得价格为 2 的商品;最后单独购买剩下的一件 价格为 1 的商品。总计花费 4 + 8 + 5 + 7 + 1 = 25 。不存在花费更低的方案。 【评测用例规模与约定】 对于 30 % 的数据, 1 ≤ N ≤ 20 。 对于 100 % 的数据, 1 ≤ N ≤ 5 × 10⁵ ,1 ≤ A i ≤ 10⁹ 。Ⅰ、题目解读
要花费最少,就要购买的商品价格高点,这样可以白嫖到更贵的商品,而不是便宜的商品。如题目所给样例:7+8(2)+4+5(1)+1=25。我认为可以使用数组储存再sort排序,然后使用二分查找到符合小于p/2的最大值,再将已经买完的商品变为0(或者其他方法标记为已购买的状态),然后不断重复上面步骤。(博主使用word打开题目,题目有问题,p/2显示的是p2,看错题目了,纯纯大冤种???)。
H、合并石子(时间限制: 1.0s 内存限制: 512.0MB)
【问题描述】 在桌面从左至右横向摆放着 N 堆石子。每一堆石子都有着相同的颜色,颜 色可能是颜色 0 ,颜色 1 或者颜色 2 中的其中一种。 现在要对石子进行合并,规定每次只能选择位置相邻并且颜色相同的两堆 石子进行合并。合并后新堆的相对位置保持不变,新堆的石子数目为所选择的 两堆石子数目之和,并且新堆石子的颜色也会发生循环式的变化。具体来说: 两堆颜色 0 的石子合并后的石子堆为颜色 1 ,两堆颜色 1 的石子合并后的石子堆为颜色 2 ,两堆颜色 2 的石子合并后的石子堆为颜色 0 。本次合并的花费为所 选择的两堆石子的数目之和。 给出 N 堆石子以及他们的初始颜色,请问最少可以将它们合并为多少堆石子?如果有多种答案,选择其中合并总花费最小的一种,合并总花费指的是在 所有的合并操作中产生的合并花费的总和。 【输入格式】 第一行一个正整数 N 表示石子堆数。 第二行包含 N 个用空格分隔的正整数,表示从左至右每一堆石子的数目。 第三行包含 N 个值为 0 或 1 或 2 的整数表示每堆石头的颜色。 【输出格式】 一行包含两个整数,用空格分隔。其中第一个整数表示合并后数目最少的 石头堆数,第二个整数表示对应的最小花费。 【样例输入】55 10 1 8 61 1 0 2 22 44【样例说明】
Ⅰ、题目解读
这题和G买二赠一有点类似,都是合并然后选择某种方法标记为已合并的状态。我举个例子(1,5)和(1,10)合并为(2,15),另一个变成已使用的状态(3,0),之后进行二维数组排序,先排石子的颜色(0,1,2),在排石子的数量(升序排),因为这样才能保证花费最小(开始合并也要进行一道排序)。不断重复上面步骤计算花费,直到没有一样的石子可以合并了(3为已使用状态不可以合并)。但是这上面有一个漏洞,我们可以看下面一组数据就懂了:(0,10),(0,11),(1,1),(1,2),(2,3);如果按照上面的思路就是先合并(0,10)和(0,11),但是我们用肉眼就可以看出来应该先合并(1,1),(1,2)->(2,3)和(3,0),然后两个(2,3)变成(0,6)和(3,0),再去合并颜色为0的石子,因此合并的时候要去寻找一下不同石子可以合并的最小费用,优先合并花费少的。
I、最大开支(时间限制: 1.0s 内存限制: 512.0MB )
【问题描述】 小蓝所在学校周边新开业了一家游乐园,小蓝作为班长,打算组织大家去 游乐园玩。已知一共有 N 个人参加这次活动,游乐园有 M 个娱乐项目,每个 项目都需要买门票后才可进去游玩。门票的价格并不是固定的,团购的人越多 单价越便宜,当团购的人数大于某个阈值时,这些团购的人便可以免费进入项 目进行游玩。这 M 个娱乐项目是独立的,所以只有选择了同一个项目的人才可 以参与这个项目的团购。第 i 个项目的门票价格 H i 与团购的人数 X 的关系可 以看作是一个函数: Hi(X) = max (Ki × X + Bi , 0) , max 表示取二者之中的最大值。当 H i = 0 时说明团购人数达到了此项目的免单阈值。 这 N 个人可以根据自己的喜好选择 M 个娱乐项目中的一种,或者有些人 对这些娱乐项目都没有兴趣,也可以选择不去任何一个项目。每个人最多只会 选择一个娱乐项目,如果多个人选择了同一个娱乐项目,那么他们都将享受对 应的团购价格。小蓝想知道他至少需要准备多少钱,使得无论大家如何选择, 他都有能力支付得起所有 N 个人购买娱乐项目的门票钱。 【输入格式】 第一行两个整数 N 、 M ,分别表示参加活动的人数和娱乐项目的个数。 接下来 M 行,每行两个整数,其中第 i 行为 K i 、 B i ,表示第 i 个游乐地点 的门票函数中的参数。 【输出格式】 一个整数,表示小蓝至少需要准备多少钱,使得大家无论如何选择项目, 自己都支付得起。 【样例输入】4 2-4 10-2 7【样例输出】
12【样例说明】
样例中有 4 个人, 2 个娱乐项目,我们用一个二元组 ( a , b ) 表示 a 个人选 择了第一个娱乐项目,b 个人选择了第二个娱乐项目,那么就有 4 − a − b 个 人没有选择任何项目,方案 ( a , b ) 对应的门票花费为 max ( − 4 × a + 10 , 0) × a + max ( − 2 × b + 7 , 0) × b ,所有的可能如下所示: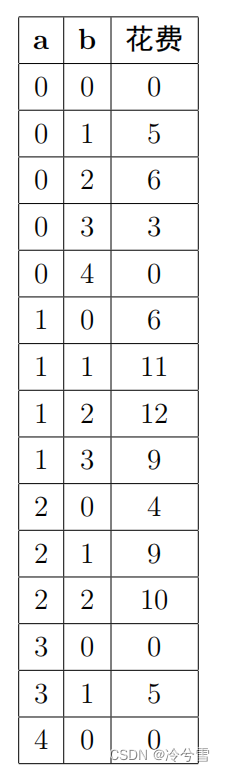
其中当 a = 1, b = 2 时花费最大,为 12。此时 1 个人去第一个项目,所以第一个项目的单价为 10 − 4 = 6,在这个项目上的花费为 6 × 1 = 6;2 个人去 第二个项目,所以第二个项目得单价为 7 − 2 × 2 = 3,在这个项目上的花费为 2 × 3 = 6;还有 1 个人没去任何项目,不用统计;总花费为 12,这是花费最大的一种方案,所以答案为 12。
【评测用例规模与约定】 对于 30 % 的评测用例, 1 ≤ N , M ≤ 10 。 对于 50 % 的评测用例, 1 ≤ N , M ≤ 1000 。 对于 100 % 的评测用例, 1 ≤ N , M , B i ≤ 10⁵ ,−10⁵ ≤ K i < 0 。
Ⅰ、题目解读
这题的解题思路就是:计算每个项目多一个人参加时造成的费用变化量,贪心的参加费用变化最多的项目。
J、魔法阵(时间限制: 1.0s 内存限制: 512.0MB )

【输入格式】
第一行输入三个整数, N , K , M ,用空格分隔。 接下来 M 行,每行包含三个整数 u , v , w ,表示结点 u 与结点 v 之间存在一 条伤害属性为 w 的无向边。 【输出格式】 输出一行,包含一个整数,表示小蓝从结点 0 到结点 N − 1 受到的最小伤 害。【样例输入 1】
4 2 30 1 21 2 12 3 4【样例输出 1】
22 5 10 1 1【样例输出 2】
0

总结
博主第一次参加蓝桥杯,还是发现自身的很多不足,比如上面几题的贪心动态规划,写的时候没有一点想法,完全跳过放弃写下一题。还有各种情况想得不是很到位,还碰上了题目显示错误的事,这是我没想到的,主办方也没有说一定使用哪个软件打开题目的啊??。道阻且长,我还需继续加油,同时也感谢各位的支持。
有官方题解我也会第一时间更新,还请兄弟们点赞收藏一番。
上面题解代码仅仅代表个人观点,有问题欢迎各位佬评论指点,或直接给出解答。万分感谢!