
本篇博客旨在整理记录自已对二叉树的一些总结,以及刷题的解题思路,同时希望可给小伙伴一些帮助。本人也是算法小白,水平有限,如果文章中有什么错误之处,希望小伙伴们可以在评论区指出来,共勉 ?。
文章目录
一、理论基础:1、常见术语2、基本操作3、种类:4、存储方式:5、遍历方式:深度优先搜索(DFS):广度优先搜索(BFS): 二、二叉查找树的创建1、二叉树的结点类2、二叉树查找树3、二叉树查找树其他便捷方法3.1、查找二叉树中最小的键3.2、查找二叉树中最大的键 三、二叉树的基础遍历1.1、前序、中序、后序遍历1.1.1、前序遍历1.1.2、中序遍历1.1.3、后序遍历 1.2、二叉树的层序遍历1.3、二叉树的最大深度问题 小结二叉树二叉树遍历 最后
一、理论基础:
【二叉树 Binary Tree】是一种非线性数据结构,代表着祖先与后代之间的派生关系,体现着“一分为二”的分治逻辑。类似于链表,二叉树也是以结点为单位存储的,结点包含【值】和两个【指针】。
/* 二叉树结点类 */class TreeNode { int val; // 结点值 TreeNode left; // 左子结点指针 TreeNode right; // 右子结点指针 TreeNode(int x) { val = x; }}结点的两个指针分别指向【左子节点 Left Child Node】 和 【右子结点 Right Child Node】,并且称该结果为两个子结点的【父结点 Parent Node】。给定二叉树某结点,将左子结点以下的树称为该结点的【左子树 Left Subtree】,右子树同理。
除了叶节点外,每个结点都有子结点和子树。例如,若将下图的【结点2】看作父结点,那么其左子结点和右子结点分别为【结点4】和【结点5】,左子树和右子树分别为【结点 4 及其以下结点形成的树】和【结点 5 及其以下结点形成的树】。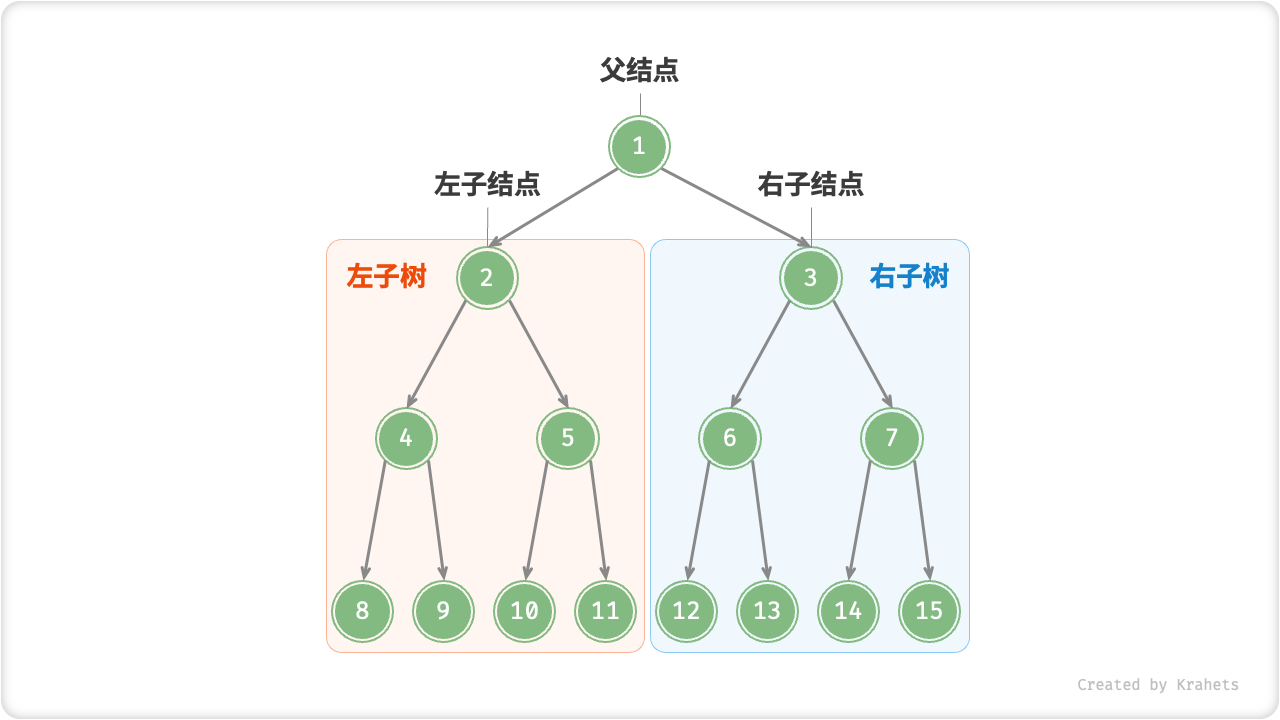
1、常见术语
二叉树的常见术语:
【根结点 Root Node】:二叉树最顶层的结点,其没有父结点;【叶节点 Leaf Node】:没有子结点的结点,其两个指针都指向(\text{null});结点所处【层 Level】:从顶至底依次增加,根结点所处层为 1;结点【度 Degree】:结点的子节结点数量。二叉树中,度的范围是0,1,2;【边 Edge】:连接两个结点的边,即结点指针;二叉树【高度】:二叉树中根结点到最远叶结点走过边的数量;结点【深度 Depth】:根结点到该结点走过边的数量;结点【高度 Height】:最远叶结点到该结点走过边的数量;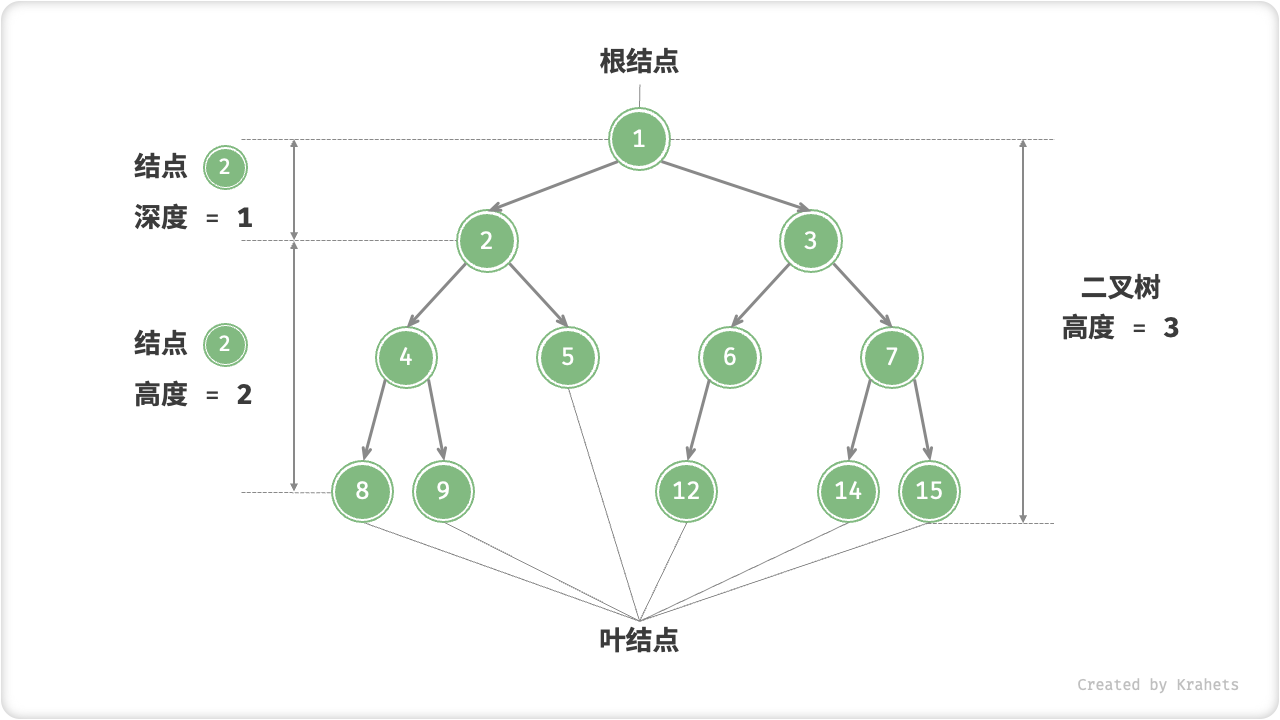
高度与深度的定义
值得注意,我们通常将「高度」和「深度」定义为“走过边的数量”,而有些题目或教材会将其定义为“走过结点的数量”,此时高度或深度都需要 + 1 。
2、基本操作
初始化二叉树。 与链表类似,先初始化结点,再构建引用指向(即指针)。
// 初始化结点TreeNode n1 = new TreeNode(1);TreeNode n2 = new TreeNode(2);TreeNode n3 = new TreeNode(3);TreeNode n4 = new TreeNode(4);TreeNode n5 = new TreeNode(5);// 构建引用指向(即指针)n1.left = n2;n1.right = n3;n2.left = n4;n2.right = n5;插入与删除结点。 与链表类似,插入与删除结点都可以通过修改指针实现。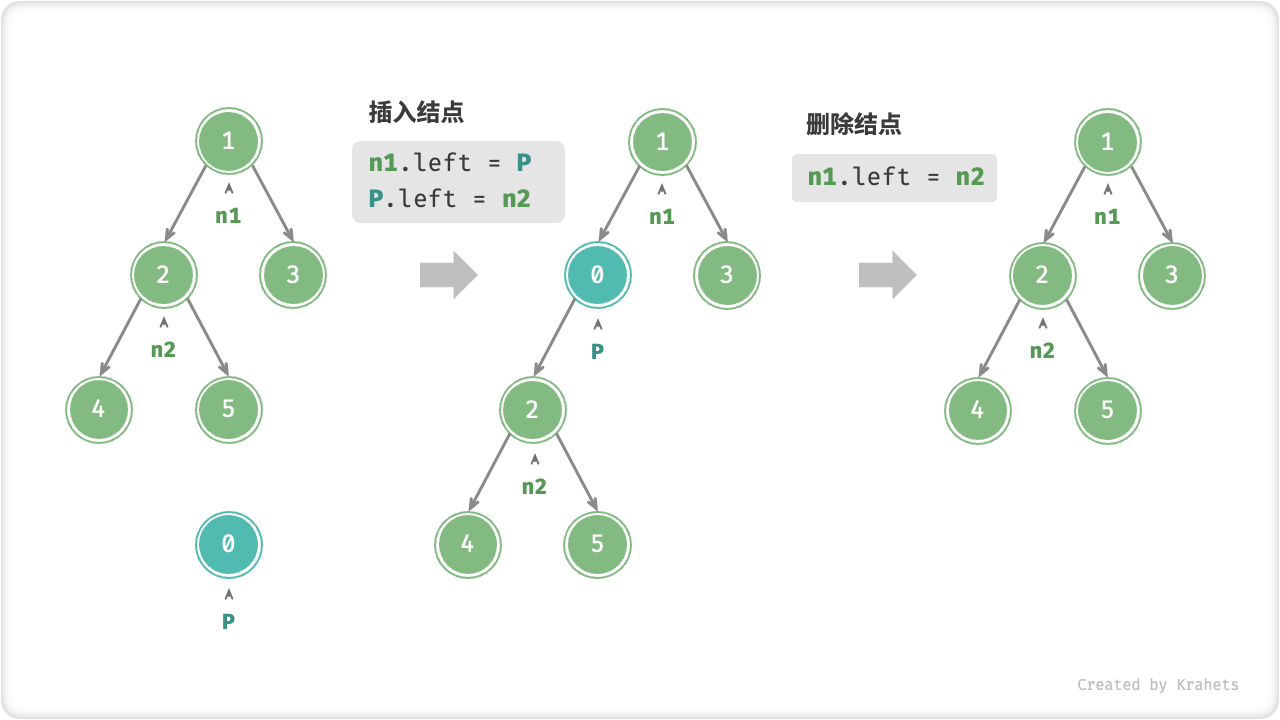
在二叉树中插入与删除结点
TreeNode P = new TreeNode(0);// 在 n1 -> n2 中间插入结点 Pn1.left = P;P.left = n2;// 删除结点 Pn1.left = n2;Note
插入结点会改变二叉树的原有逻辑结构,删除结点往往意味着删除了该结点的所有子树。因此,二叉树中的插入与删除一般都是由一套操作配合完成的,这样才能实现有意义的操作。
3、种类:
满二叉树: 如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。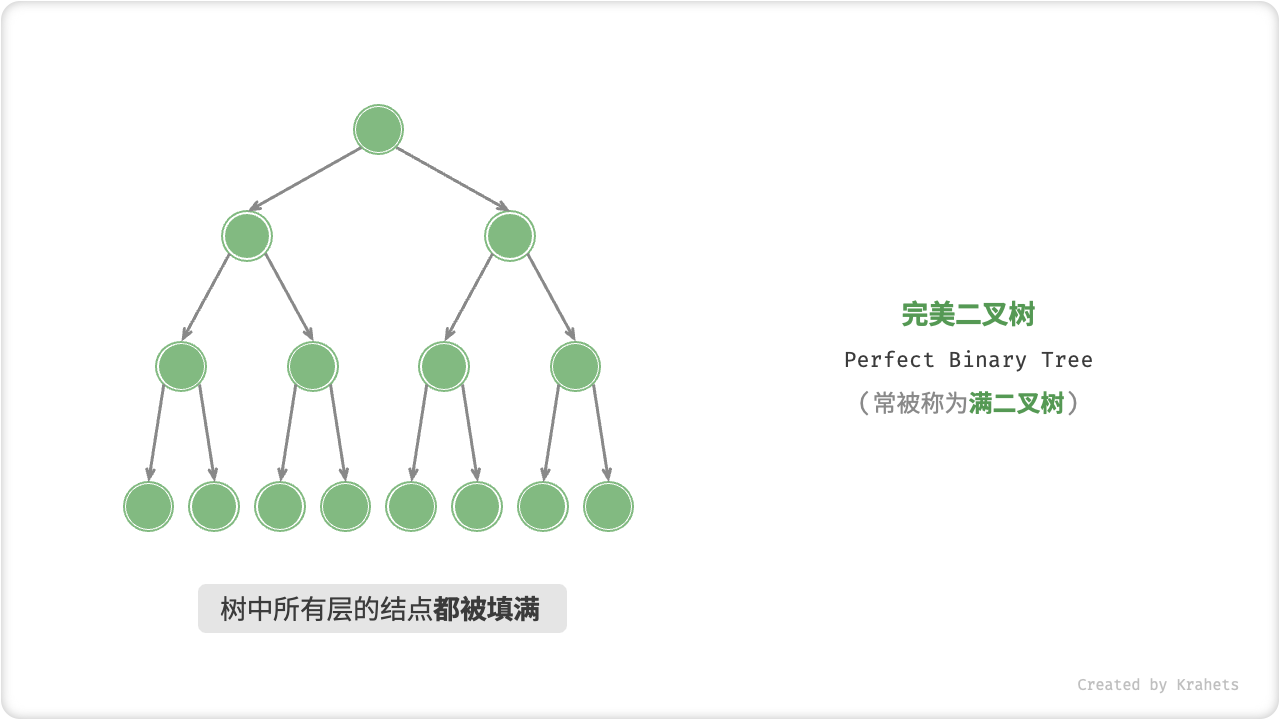
完全二叉树: 在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2^(h-1) 个节点。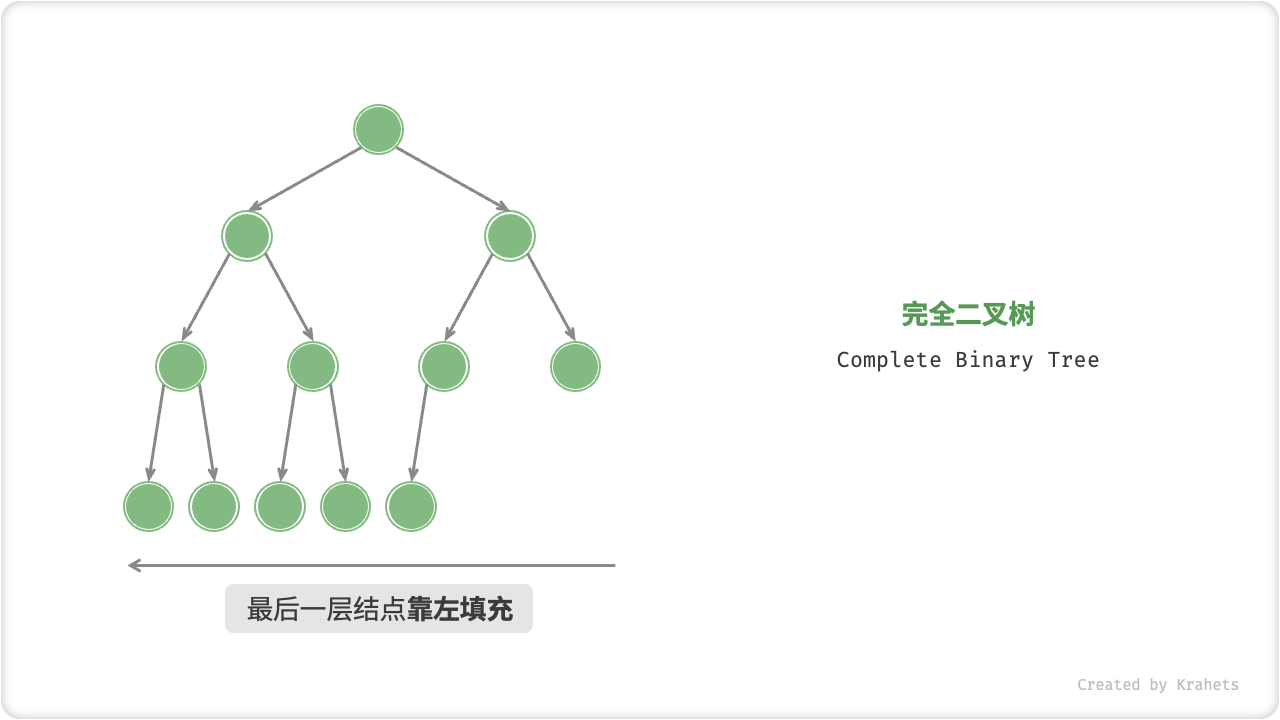
二叉搜索树: 二叉搜索树是一个有序树。
平衡二叉搜索树: 平衡二叉搜索树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。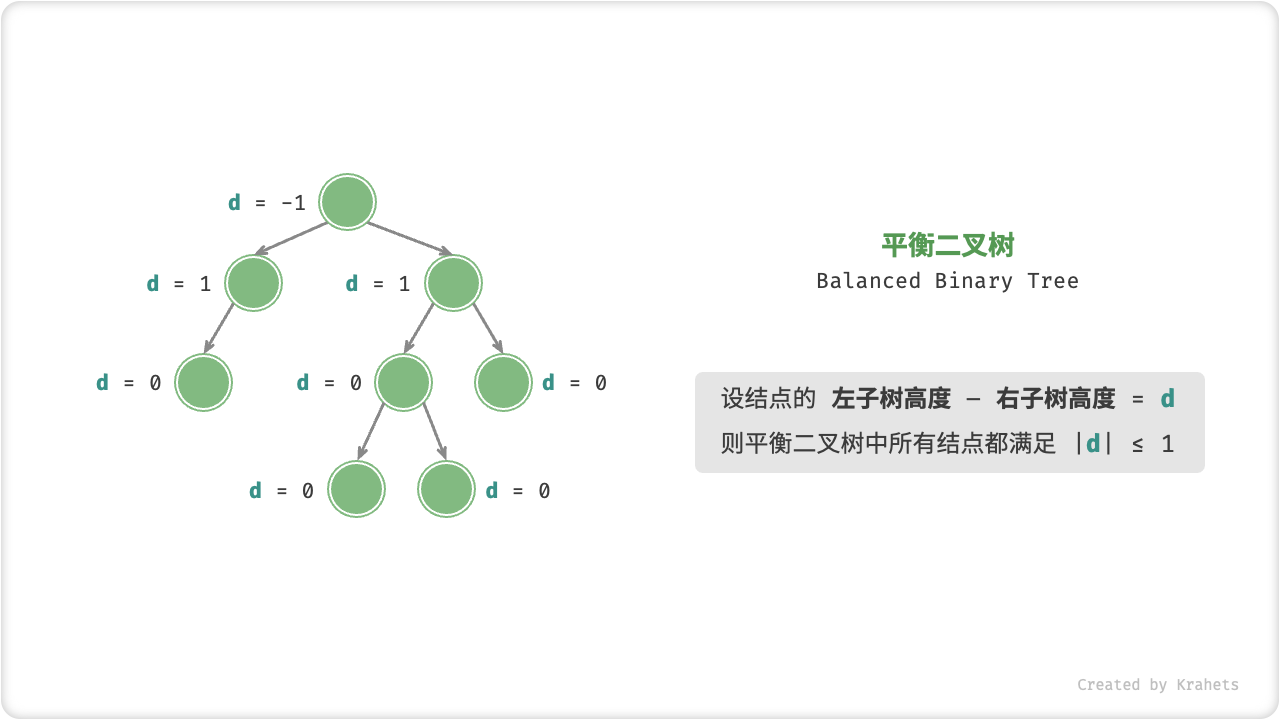
4、存储方式:
线性存储【数组】、链式存储【指针】
5、遍历方式:
二叉树的遍历分为深度优先搜索和广度优先搜索
深度优先搜索(DFS):
1、前序遍历 中 左 右
2、中序遍历 左 中 右
3、后序遍历 左 右 中
广度优先搜索(BFS):
1、层序遍历
二叉树递归解题方法:
二、二叉查找树的创建
1、二叉树的结点类
根据对图的观察,我们发现二叉树其实就是由一个一个的结点及其之间的关系组成的,按照面向对象的思想,我们设计一个结点类来描述结点这个事物。
节点类API设计:
| 类名 | Node<Key, Value> |
|---|---|
| 构造方法 | Node(Key key, Value value, Node left, Node right) |
| 成员变量 | 1. public Node left:记录左子结点 2.public Node right:记录右子结点 3.public Key key:存储键 4.public Value value:存储值 |
| 代码实现: |
private class Node<Key, Value> { // 存储键 public Key key; // 存储值 private Value value; // 记录左子结点 public Node left; // 记录右子结点 public Node right; public Node(Key key, Value value, Node left, Node right) { this.key = key; this.value = value; this.left = left; this.right = right; } }2、二叉树查找树
二叉树查找树API设计
| 类名 | <BinaryTree,Value value> |
|---|---|
| 构造方法 | BinaryTree():创建BinaryTree对象 |
| 成员变量 | 1. private Node root:记录根结点 ;2. private int N:记录数中元素的个数 |
| 成员方法 | 1. public void put(Key key,Value value):向树中插入一个键值对; 2. private Node put(Node x, Key key, Value val):给指定树x上,添加键一个键值对,并返回添加后的新树;3. public Value get(Key key):根据key,从树中找出对应的值; 4. private Value get(Node x, Key key):从指定的树x中,找出key对应的值; 5. public void delete(Key key):根据key,删除树中对应的键值对; 6. private Node delete(Node x, Key key):删除指定树x上的键为key的键值对,并返回删除后的新树; 7. public int size():获取树中元素的个数; |
二叉查找树实现
插入方法put实现思想 :
如果当前树中没有任何一个结点,则直接把新结点当做根结点使用如果当前树不为空,则从根结点开始: 如果新结点的key小于当前结点的key,则继续找当前结点的左子结点 ;如果新结点的key大于当前结点的key,则继续找当前结点的右子结点如果新结点的key等于当前结点的key,则树中已经存在这样的结点,替换该结点的value值即可.查询方法get实现思想 :
从根节点开始:
删除方法delete实现思想 :
找到被删除结点;找到被删除结点右子树中的最小结点minNode删除右子树中的最小结点让被删除结点的左子树称为最小结点minNode的左子树,让被删除结点的右子树称为最小结点minNode的右子树让被删除结点的父节点指向最小结点minNode代码实现:
/** * @author QIA * @create 2023-04-04-1:43 */public class BinaryTree<Key extends Comparable<Key>, Value> { // 记录根结点 private Node root; // 记录树中元素的个数 private int N; private class Node { // 存储键 public Key key; // 存储值 private Value value; // 记录左子结点 public Node left; // 记录右子结点 public Node right; public Node(Key key, Value value, Node left, Node right) { this.key = key; this.value = value; this.left = left; this.right = right; } } // 获取树中元素的个数 public int size() { return N; } // 向树中添加元素key-value public void put(Key key, Value value) { root = put(root, key, value); } // 向指定的树x中添加key-value,并返回添加元素后新的树 private Node put(Node x, Key key, Value value) { // 如果x子树为空 if (x == null) { // 个数+1 N++; return new Node(key, value, null, null); } // 如果 x 子树不为空 // 比较 x 结点的键和 key 的大小: int cmp = key.compareTo(x.key); if (cmp > 0) { // 新结点的 key 大于当前结点的 key ,继续找当前结点的右子结点 x.right = put(x.right, key, value); }else if(cmp < 0) { // 新结点的 key 小于当前结点的 key ,继续找当前结点的左子结点 x.left = put(x.left, key, value); }else { // 新结点的 key 等于当前结点的 key ,把当前结点的 value 进行替换 x.value = value; } return x; } // 查询树中指定 key 对应的value public Value get(Key key) { return get(root,key); } // 从指定的树x中,查找key对应的值 public Value get(Node x, Key key) { // x树为null if (x == null) { return null; } // x树不为null // 比较key和x结点的键的大小 int cmp = key.compareTo(x.key); if (cmp > 0) { // 如果 key大于 x 结点的键,则继续找 x 结点的右子树 return get(x.right, key); }else if(cmp < 0) { // 如果 key 小于 x 结点的键,则继续找 x 结点的左子树 return get(x.left, key); }else { // 如果 key 等于 x 结点的键,就找到了键为key的结点,只需要返回x结点的值即可 return x.value; } } // 删除树中key对应的value public void delete(Key key) { root = delete(root, key); } // 删除指定树 x 中的 key 对应的 value,并返回删除后的新树 public Node delete(Node x, Key key) { if (x == null) { return null; } int cmp = key.compareTo(x.key); if (cmp > 0) { /// 新结点的 key 大于当前结点的 key ,继续找当前结点的右子结点 x.right = delete(x.right, key); }else if(cmp < 0) { // 新结点的 key 小于当前结点的 key ,继续找当前结点的左子结点 x.left = delete(x.left, key); }else { // 新结点的 key 等于当前结点的 key ,当前 x 就是要删除的结点 // 1.如果当前结点的右子树不存在,则直接返回当前节点的左子节点 if (x.right == null) { return x.left; } // 2.如果当前结点的左子树不存在,则直接返回当前结点的右子结点 if (x.left == null) { return x.right; } // 3.当前结点的左右子树都存在 // 3.1 找到右子树中最小的结点 Node minNode = x.left; while (minNode.left != null) { minNode = minNode.left; } // 3.2 删除右子树中最小的结点 Node n = x,right; while (n.left != null) { if (n.left.left == null) { n.left = null; } else { n = n.left; } } // 3.3 让被删除结点的左子树被称为最小结点minNode的左子树,让被删除结点的右子树称为最小结点minNode的右子树 minNode.left = x.left; minNode.right = x.right; // 3.4 让删除结点的父节点指向最小结点minNode x = minNode; // 个数-1 N--; } return x; } public static void main(String[] args) { BinaryTree<Integer, String> bt = new BinaryTree<>(); bt.put(4, "二哈"); bt.put(1, "张三"); bt.put(3, "李四"); bt.put(5, "王五"); // 长度 System.out.println(bt.size()); bt.put(1, "老三"); System.out.println(bt.get(1)); System.out.println(bt.size()); bt.delete(1); System.out.println(bt.size()); }}3、二叉树查找树其他便捷方法
3.1、查找二叉树中最小的键
| public Key min() | 找出树中最小的键 |
|---|---|
| private Node min(Node x) | 找出指定树x中,最小键所在的结点 |
//找出整个树中最小的键public Key min(){return min(root).key;}//找出指定树x中最小的键所在的结点private Node min(Node x){ if (x.left!=null){ return min(x.left); }else{ return x; }}3.2、查找二叉树中最大的键
| public Kye max() | 找出树中最大的键 |
|---|---|
| public Node max(Node x) | 找出指定树x中,最大键所在的结点 |
//找出整个树中最大的键public Key max(){return max(root).key;}//找出指定树x中最大键所在的结点public Node max(Node x){ if (x.right!=null){ return max(x.right); }else{ return x; }}三、二叉树的基础遍历
从物理结构角度看,树是一种基于链表的数据结构,因此遍历方式也是通过指针(即引用)逐个遍历结点。同时,树还是一种非线性数据结构,这导致遍历树比遍历链表更加复杂,需要使用搜索算法来实现。
常见的二叉树遍历方式有前序遍历、中序遍历、后序遍历、层序遍历。
1.1、前序、中序、后序遍历
前、中、后序遍历皆属于[深度优先遍历Depth-First Traversal],其体现着一种”先走到尽头,再回头继续“的回溯遍历方式。
如下图所示,左侧是深度优先遍历的的示意图,右上方是对应的递归实现代码。深度优先遍历就像是绕着整个二叉树的外围“走”一圈,走的过程中,在每个结点都会遇到三个位置,分别对应前序遍历、中序遍历、后序遍历。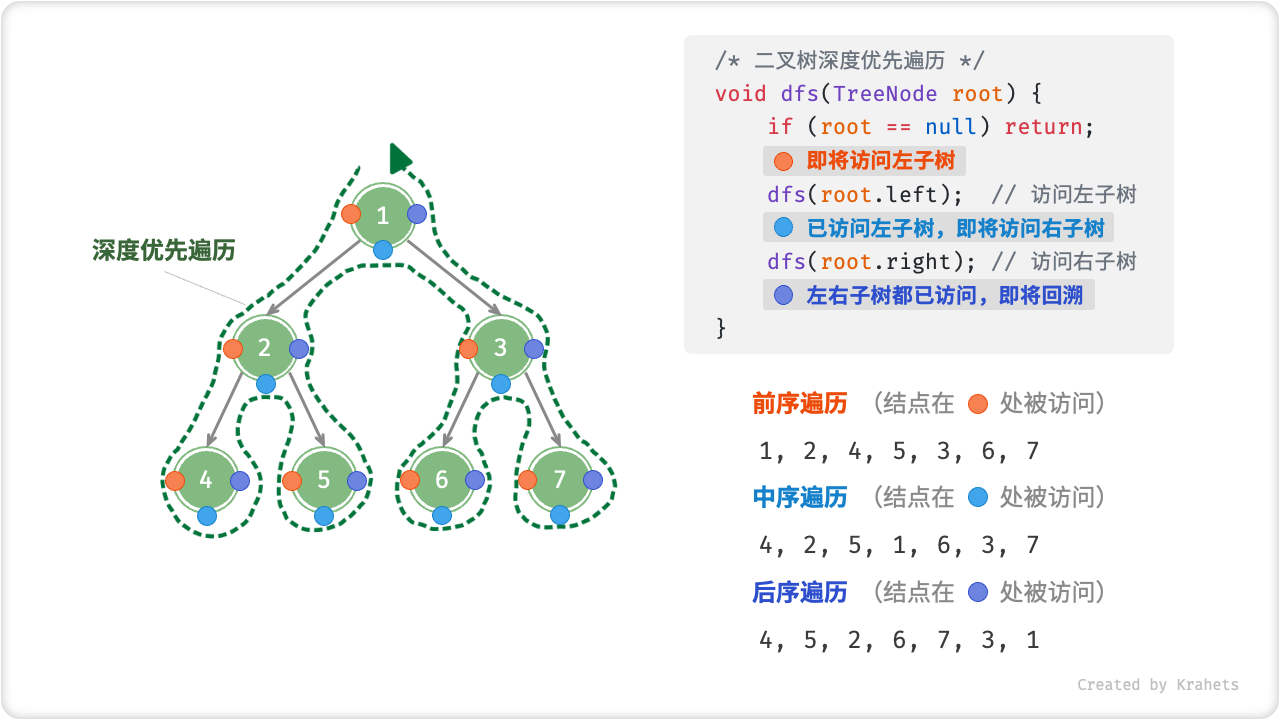
复杂度分析
时间复杂度: 所有结点被访问一次,使用O(n)时间,其中n为结点数量。
空间复杂度: 当树退化为链表时达到最差情况,递归深度达到n,系统使用O(nb)栈帧空间。
1.1.1、前序遍历
添加前序遍历的API:public Queue<Key> preErgodic():使用前序遍历,获取整个树中的所有键private void preErgodic(Node x,Queue<Key> keys):使用前序遍历,把指定树x中的所有键放入到keys队列中
实现过程中,我们通过前序遍历,把每个结点的键取出,放入到队伍中返回即可。
实现步骤:
代码:
//使用前序遍历,获取整个树中的所有键public Queue<Key> preErgodic(){ Queue<Key> keys = new Queue<>(); preErgodic(root,keys); return keys;}//使用前序遍历,把指定树x中的所有键放入到keys队列中private void preErgodic(Node x,Queue<Key> keys){ if (x==null){ return; } // 1.把当前结点的key放入到队列中; keys.enqueue(x.key); // 2.找到当前结点的左子树,如果不为空,递归遍历左子树 if (x.left!=null){ preErgodic(x.left,keys); } // 3.找到当前结点的右子树,如果不为空,递归遍历右子树 if (x.right!=null){ preErgodic(x.right,keys); }}//测试代码public class Test { public static void main(String[] args) throws Exception { BinaryTree<String, String> bt = new BinaryTree<>(); bt.put("E", "5"); bt.put("B", "2"); bt.put("G", "7"); bt.put("A", "1"); bt.put("D", "4"); bt.put("F", "6"); bt.put("H", "8"); bt.put("C", "3"); Queue<String> queue = bt.preErgodic(); for (String key : queue) { System.out.println(key+"="+bt.get(key)); } }}1.1.2、中序遍历
添加中序遍历的API:public Queue<Key> midErgodic():使用中序遍历,获取震哥哥树中的所有键private void midErgodic(Node x, Queue<Key> keys):使用中序遍历,把指定树x中的所有键放入到keys队列中
实现步骤:
代码:
//使用中序遍历,获取整个树中的所有键public Queue<Key> midErgodic(){Queue<Key> keys = new Queue<>();midErgodic(root,keys); return keys;}//使用中序遍历,把指定树x中的所有键放入到keys队列中private void midErgodic(Node x,Queue<Key> keys){ if (x==null){ return; } // 1.找到当前结点的左子树,如果不为空,递归遍历左子树 if (x.left!=null){ midErgodic(x.left,keys); } // 2.把当前结点的key放入到队列中; keys.enqueue(x.key); // 3.找到当前结点的右子树,如果不为空,递归遍历右子树 if (x.right!=null){ midErgodic(x.right,keys); }}//测试代码public class Test { public static void main(String[] args) throws Exception { BinaryTree<String, String> bt = new BinaryTree<>(); bt.put("E", "5"); bt.put("B", "2"); bt.put("G", "7"); bt.put("A", "1"); bt.put("D", "4"); bt.put("F", "6"); bt.put("H", "8"); bt.put("C", "3"); Queue<String> queue = bt.midErgodic(); for (String key : queue) { System.out.println(key+"="+bt.get(key)); } }}1.1.3、后序遍历
添加后序遍历的API:public Queue<Key> afterErgodic():使用后序遍历,获取整个树中的所有键private void afterErgodic(Node x,Queue<Key> keys):使用后序遍历,把指定树x中的所有键放入到keys队列中
实现步骤:
代码:
//使用后序遍历,获取整个树中的所有键public Queue<Key> afterErgodic(){ Queue<Key> keys = new Queue<>(); afterErgodic(root,keys); return keys;}//使用后序遍历,把指定树x中的所有键放入到keys队列中private void afterErgodic(Node x,Queue<Key> keys){ if (x==null){ return; } //1.找到当前结点的左子树,如果不为空,递归遍历左子树 if (x.left!=null){ afterErgodic(x.left,keys); } //2.找到当前结点的右子树,如果不为空,递归遍历右子树 if (x.right!=null){ afterErgodic(x.right,keys); } //3.把当前结点的key放入到队列中; keys.enqueue(x.key);}//测试代码public class Test { public static void main(String[] args) throws Exception { BinaryTree<String, String> bt = new BinaryTree<>(); bt.put("E", "5"); bt.put("B", "2"); bt.put("G", "7"); bt.put("A", "1"); bt.put("D", "4"); bt.put("F", "6"); bt.put("H", "8"); bt.put("C", "3"); Queue<String> queue = bt.afterErgodic(); for (String key : queue) { System.out.println(key+"="+bt.get(key)); } }}1.2、二叉树的层序遍历
「层序遍历 Level-Order Traversal」从顶至底、一层一层地遍历二叉树,并在每层中按照从左到右的顺序访问结点。
层序遍历本质上是「广度优先搜索 Breadth-First Traversal」,其体现着一种“一圈一圈向外”的层进遍历方式。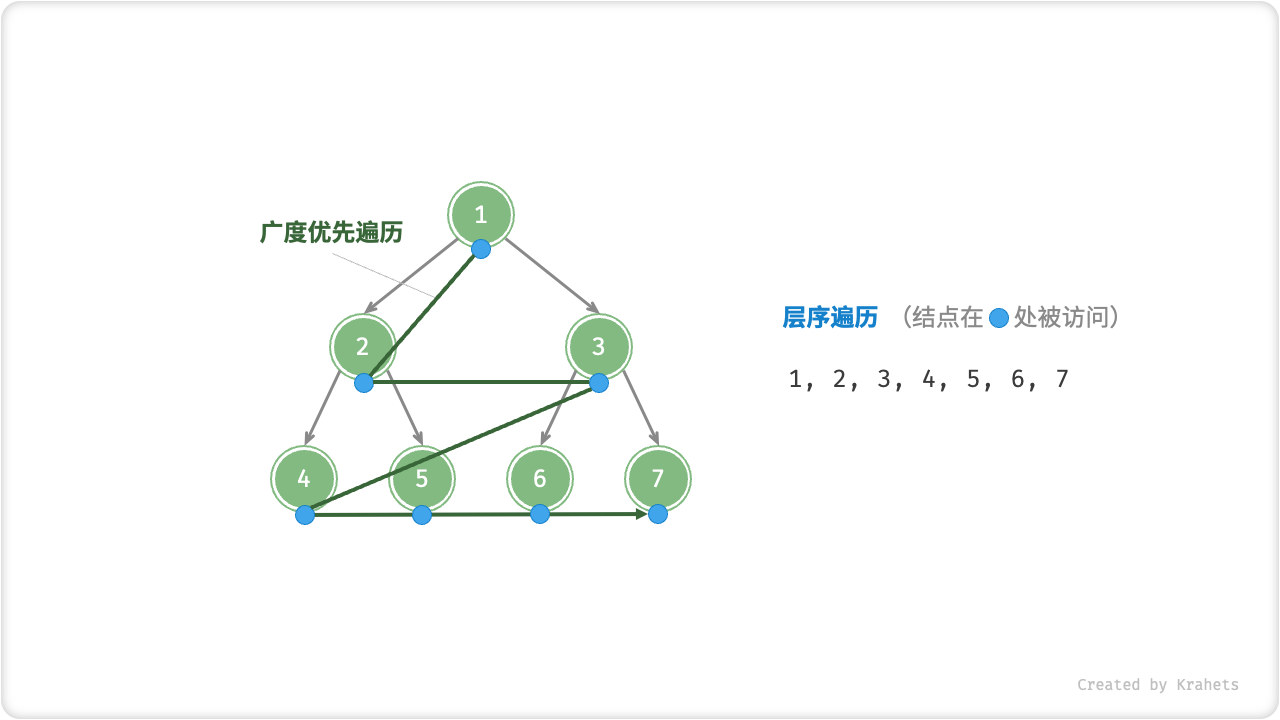
算法实现
广度优先遍历一般借助「队列」来实现。队列的规则是“先进先出”,广度优先遍历的规则是 ”一层层平推“ ,两者背后的思想是一致的。
复杂度分析
时间复杂度: 所有结点被访问一次,使用O(n)时间,其中n为结点数量。
空间复杂度: 当为满二叉树时达到最差情况,遍历到最底层前,队列中最多同时存在n+1/2 个结点,使用O(n)空间。
添加层序遍历的API:public Queue<Key> layerErgodic():使用层序遍历,获取整个树中的所有键
实现步骤:
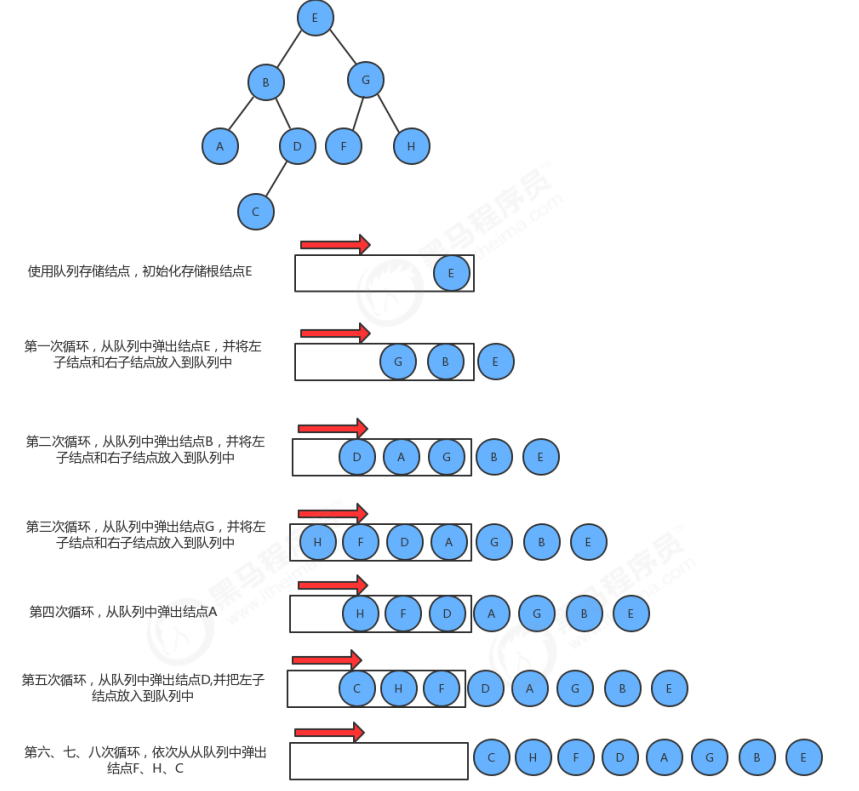
代码:
//使用层序遍历得到树中所有的键public Queue<Key> layerErgodic(){ Queue<Key> keys = new Queue<>(); Queue<Node> nodes = new Queue<>(); nodes.enqueue(root); while(!nodes.isEmpty()){ Node x = nodes.dequeue(); keys.enqueue(x.key); if (x.left!=null){ nodes.enqueue(x.left); } if (x.right!=null){ nodes.enqueue(x.right); } } return keys;}//测试代码public class Test { public static void main(String[] args) throws Exception { BinaryTree<String, String> bt = new BinaryTree<>(); bt.put("E", "5"); bt.put("B", "2"); bt.put("G", "7"); bt.put("A", "1"); bt.put("D", "4"); bt.put("F", "6"); bt.put("H", "8"); bt.put("C", "3"); Queue<String> queue = bt.layerErgodic(); for (String key : queue) { System.out.println(key+"="+bt.get(key)); } }}1.3、二叉树的最大深度问题
需求:
给定一棵树,请计算树的最大深度(树的根节点到最远叶子结点的最长路径上的结点数);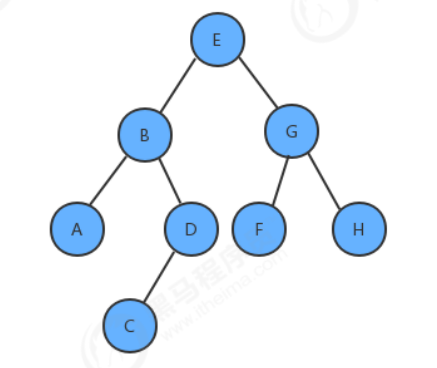
上面这棵树的最大深度为4
实现:
添加API求最大深度:public int maxDepth():计算整个数的最大深度private int maxDepth(Node x):计算指定树x的最大深度
实现步骤:
代码:
//计算整个树的最大深度public int maxDepth() {return maxDepth(root);}//计算指定树x的最大深度private int maxDepth(Node x) { //1.如果根结点为空,则最大深度为0; if (x == null) { return 0; } int max = 0; int maxL = 0; int maxR = 0; //2.计算左子树的最大深度; if (x.left != null) { maxL = maxDepth(x.left); } //3.计算右子树的最大深度; if (x.right != null) { maxR = maxDepth(x.right); } //4.当前树的最大深度=左子树的最大深度和右子树的最大深度中的较大者+1 max = maxL > maxR ? maxL + 1 : maxR + 1; return max;}//测试代码public class Test { public static void main(String[] args) throws Exception { BinaryTree<String, String> bt = new BinaryTree<>(); bt.put("E", "5"); bt.put("B", "2"); bt.put("G", "7"); bt.put("A", "1"); bt.put("D", "4"); bt.put("F", "6"); bt.put("H", "8"); bt.put("C", "3"); int i = bt.maxDepth(); System.out.println(i); }}小结
二叉树
二叉树是一种非线性数据结构,代表着“一分为二”的分治逻辑。二叉树的结点包含「值」和两个「指针」,分别指向左子结点和右子结点。选定二叉树中某结点,将其左(右)子结点以下形成的树称为左(右)子树。二叉树的术语较多,包括根结点、叶结点、层、度、边、高度、深度等。二叉树的初始化、结点插入、结点删除操作与链表的操作方法类似。常见的二叉树类型包括完美二叉树、完全二叉树、完满二叉树、平衡二叉树。完美二叉树是理想状态,链表则是退化后的最差状态。二叉树可以使用数组表示,具体做法是将结点值和空位按照层序遍历的顺序排列,并基于父结点和子结点之间的索引映射公式实现指针。二叉树遍历
二叉树层序遍历是一种广度优先搜索,体现着“一圈一圈向外”的层进式遍历方式,通常借助队列来实现。前序、中序、后序遍历是深度优先搜索,体现着“走到头、再回头继续”的回溯遍历方式,通常使用递归实现。最后
参考资料:《Hello 算法 (hello-algo.com)》对各位小伙伴有帮助的话,希望可以点赞❤️+收藏⭐,谢谢各位大佬~~???